| 時間依存輻射輸送方程式により、 AGB 星の赤外スペクトルの進化を追った。 簡単なマスロス式を使い、中間質量星の AGB 進化を計算した。結果を IRAS の 測光、分光データと比較した。 | 広範なデータを用い、マスロス式の妥当性を調べた。現在のマスロス式の結 果から、10 μm 吸収帯を示す AGB 星は Mms > 3 Mo であることが分かった |
|
タイムスケール 輻射輸送方程式を用いて星周シェルスペクトルを求める多くの研究があるが、 全て静的な配置を仮定している。しかし、AGB 星の進化は急速でそれでは 不十分である。中間質量星は < 107 年以下の時間で AGB 先端に 達すると考えられている。この短い時間内で光度は10倍に上がり、有効温度は 半分に、マスロス率は3桁上がる。力学時間 105 の星周層の構造は 中心星の変化を反映することは大いにありそうである。AGB 進化末期には 時間依存性は特に重要になる。 |
Bedijn モデル Bedijn 1986, Bedijn (1987) は、AGB 星が L, Teff 一定でマスロス率が時間変化するという仮定で、輻射輸達 方程式を解き、IRAS カラーと比較した。その結果、彼はマスロス式 dM/dt = (dM/dt)o (1 - t/to)-1 を得た。この「加速マスロス式」は彼により AGB 最後の 105 年に 適用された。この計算の欠陥は、星風が外層質量を剥ぎとるのに、恒星質量を 全期間で一定と仮定していたことである。 マスロスと殻燃焼 観測されるマスロス率は少なくともシェル燃焼が外層質量を食べる速度には 達している。dM/dt ≥ 10-6 Mo/yr の場合には、マスロスが進化 の支配権を握る。したがって、マスロスと殻燃焼の二つの効果を考慮したモデル が必要である。 |
|
LRS 分類 LRSC =Catalog of Low Resolution Spectra 1986 には 5425 個のスペクト ルが含まれている。 2113/5425 は 10 μm シリケイト帯を示す。そのいく つかは YSO がらみだが、大部分は AGB に関連する。スペクトルは二桁の数字 で分類されている。それらは 1.20-29: 1783 個。10 μ 放射帯 + 「青」連続光。M-星+星周層 2.30-39: 230 個。10 μ 吸収帯 + 「青」連続光。M-星+厚い星周層 3.60-69: 78 個。10 μ 放射帯 + 赤連続光。M-星+より厚い星周層 4.70-79: 70-79.10 μ 吸収帯 + 赤連続光。M-星+最も厚い星周層 (60-69 = 厚くて放射? ) |
カラー温度 「青」から「赤」へとカラー温度は下がる。クラス 20 から 30 にかけて、 10 μm 放射から吸収へと移るにつれカラー温度は低下して行く。 クラス 70 天体は一層カラー温度が低い。クラス 60 は解釈が難しい。 連続光は低温で厚いシェルを意味する一方、放射帯は薄い光学的厚みを意味 するからである。その問題は後の論文で議論する。 HIIR? クラス 30 と 70 =「赤い」天体の幾つかが HIIR と混同される可能性は ある。クラス30天体はまた幾つかの K-型またはより早期の星を含む。近く の分子雲からの混入があるのかも知れない。 |

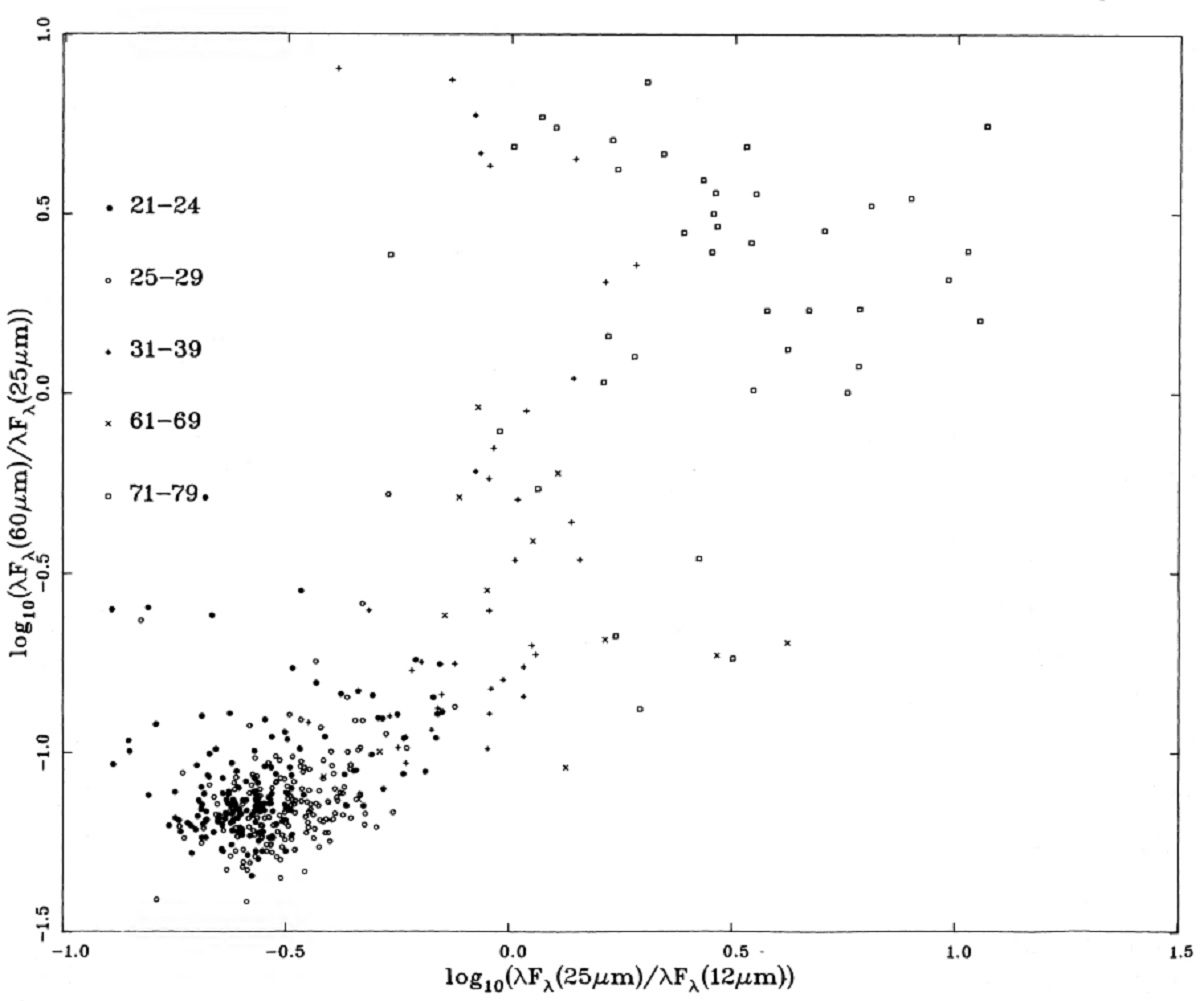
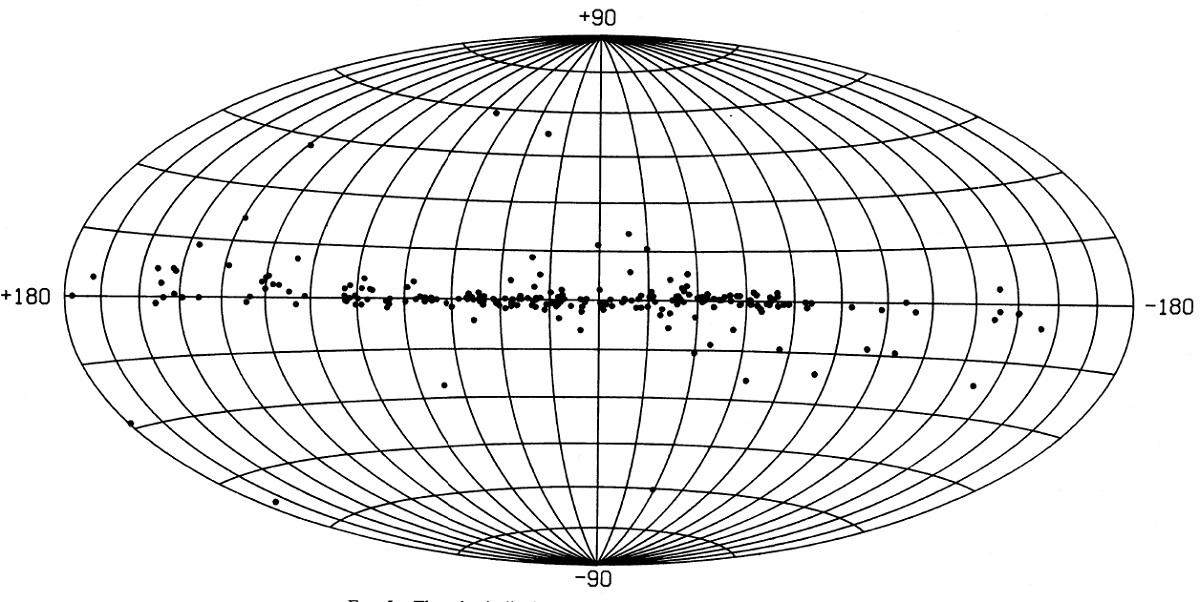
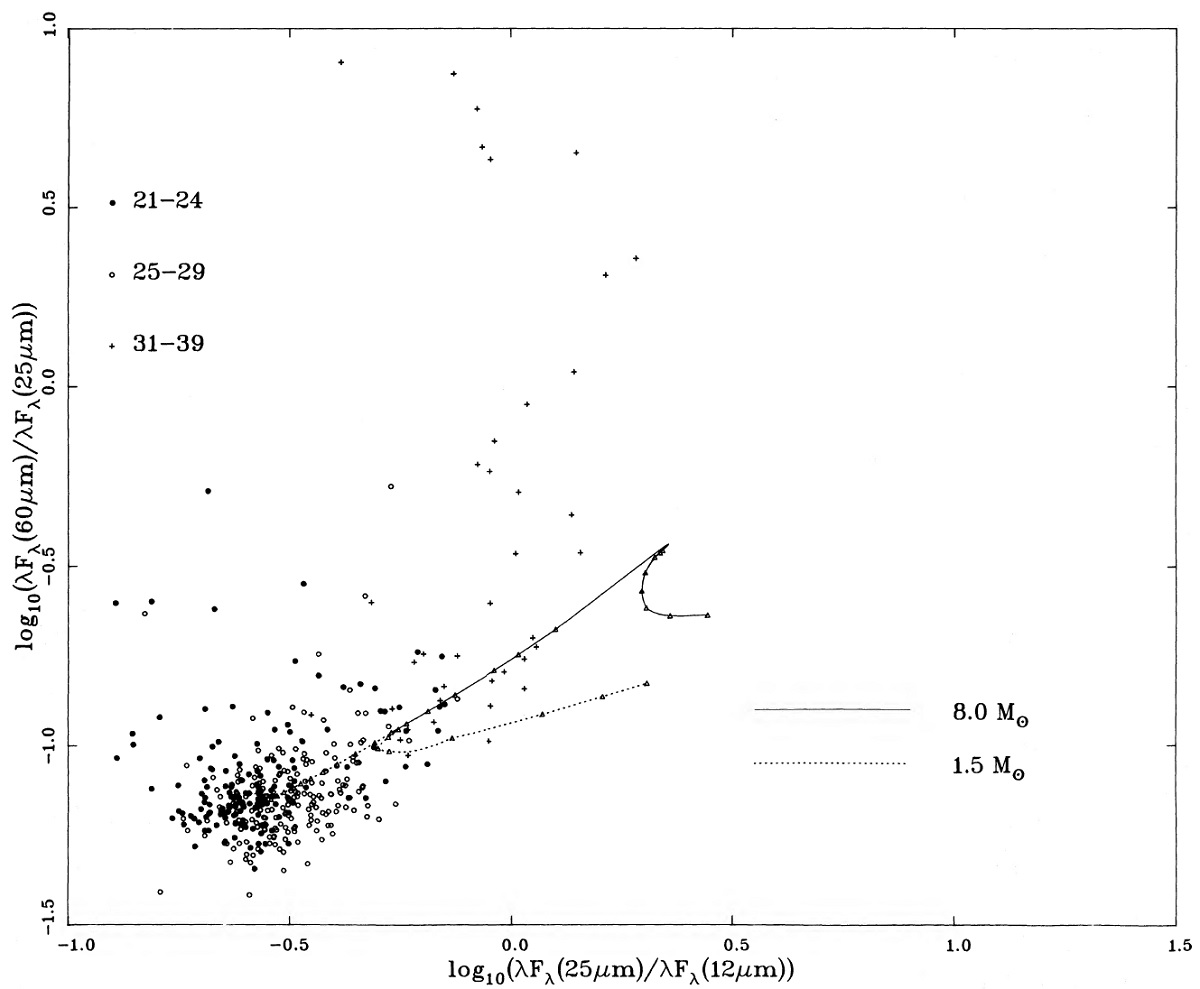
2.1.作業サンプル作業サンプル=IRAS IQ が全バンドで良いサンプル。シリケイトバンド 2113 星中の 467 天体。 467 = 179(21-24) + 196(25-29) + 38(31-39) + 14(61-69) + 40(71-79) 全 LRS 星に比べると作業サンプルでは 25 - 29 サンプルの割合が減っている 2.2.カラー分布クラス20天体図1,2に IRAS 二色図を示す。図1=12/25/60 図の左下に 21-29 天体が 固まっている。25-29 天体は 21-24 天体より広く散らばり、 21-24 天体は 25-29 天体の右側に中心があるように見える。 (これは少し理解できない記述。自己吸収は? ) |
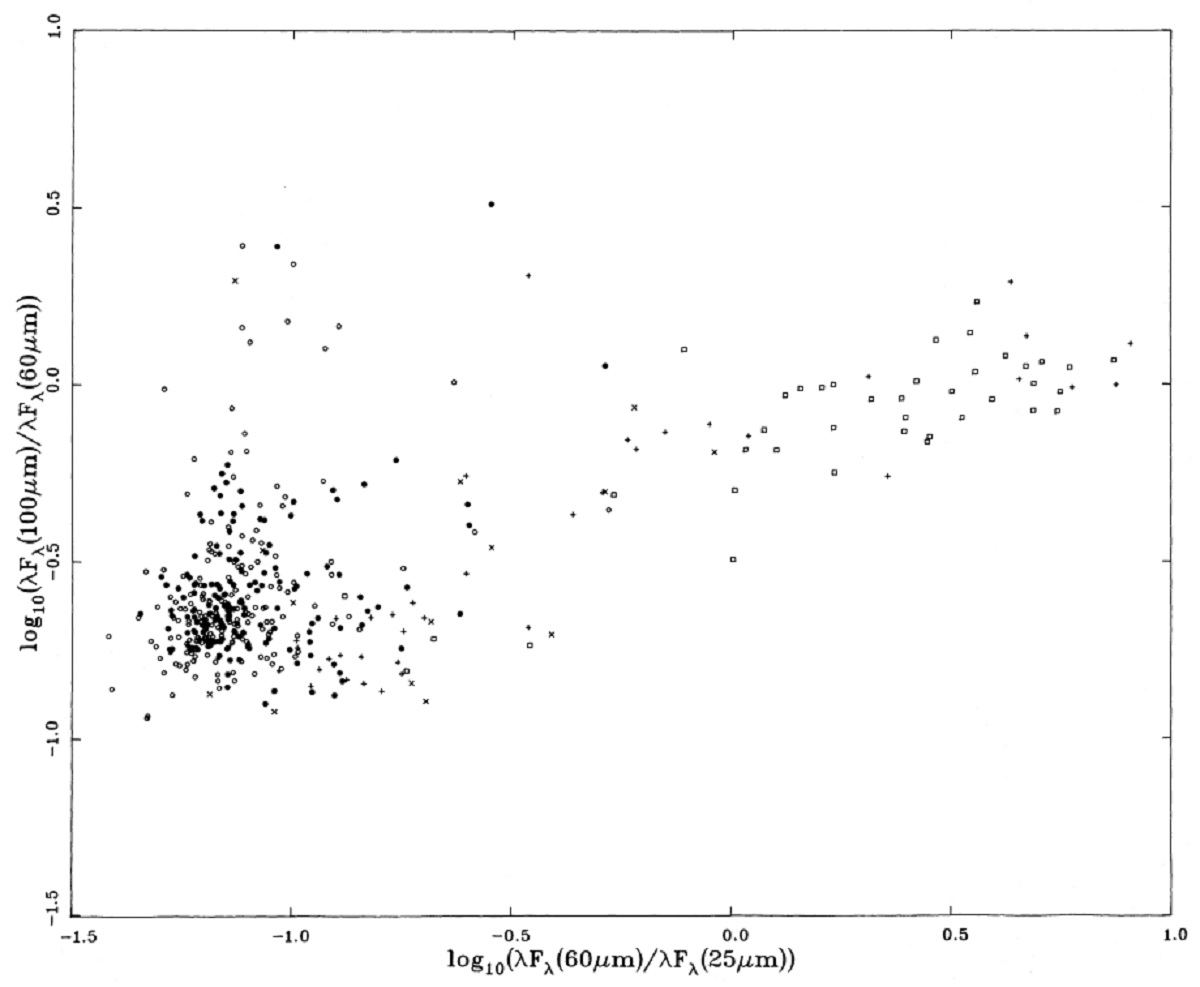
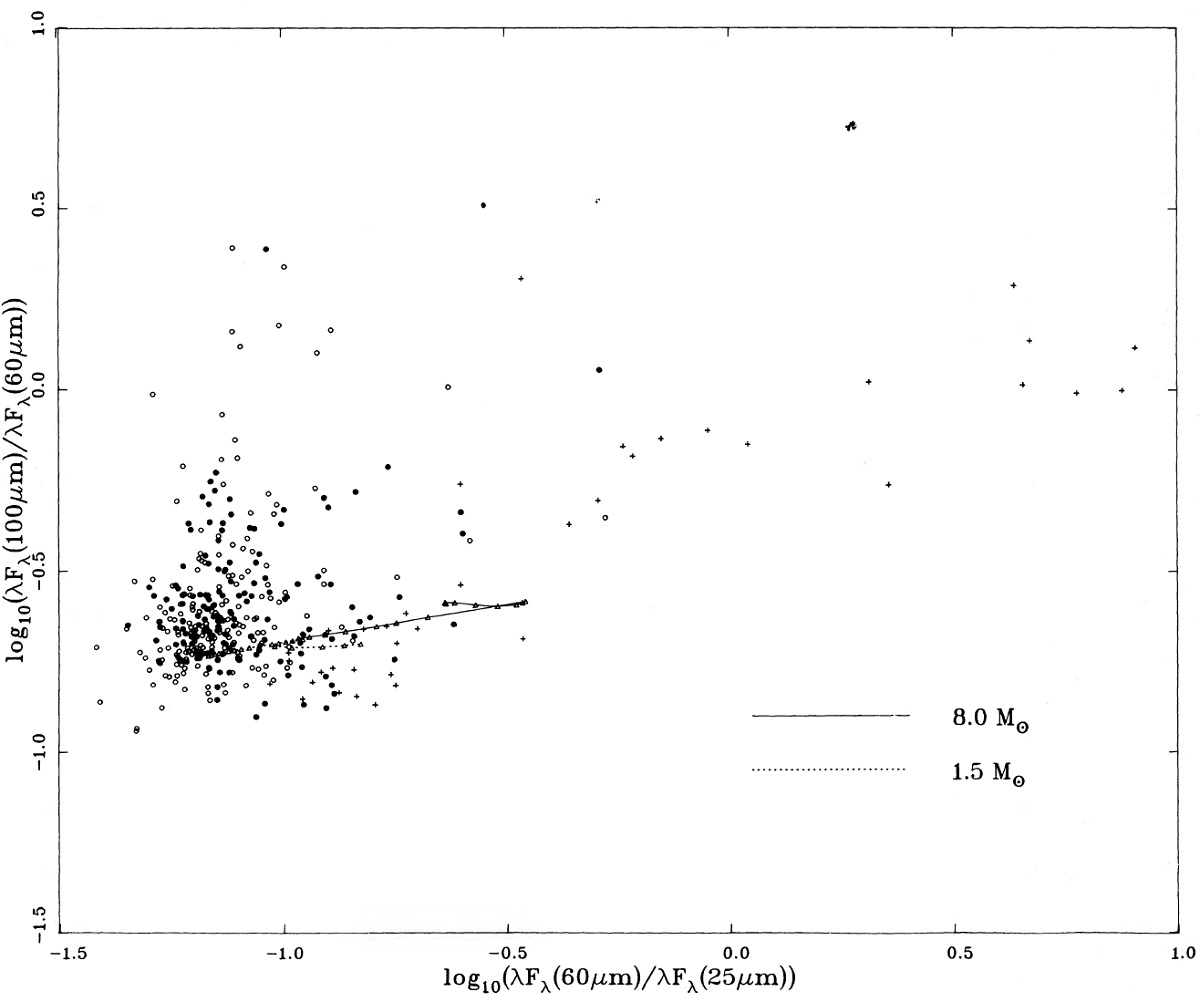
クラス30天体 クラス30はクラス20の右上を占める。その中にはいくつかの HIIRs が 混ざっている。 クラス70天体 クラス70天体はクラス30からさらに右上に離れている。幾つかはクラス 30の右側に位置するが、大部分は右上にある。40%は HIIR 天体である。 図1を見ると、クラス20から 70にかけて "S" 字型の経路が見えるが、 混入の多さを考えると怪しい。 クラス60天体 クラス60天体は図1上で塊を作らない。 図2の系列 図2は図1ほどクラスによる分離が明確でない。興味深いことに、、 F100 超過が大きなクラス20天体が多数存在する。しかし、それらは、 シラスの混入が強かった。 図2の log[(νFν)60/(νFν)25] = -0.3 が HIIRs と AGBs との境界かも知れない。 (図3の数字と違う。 ) |
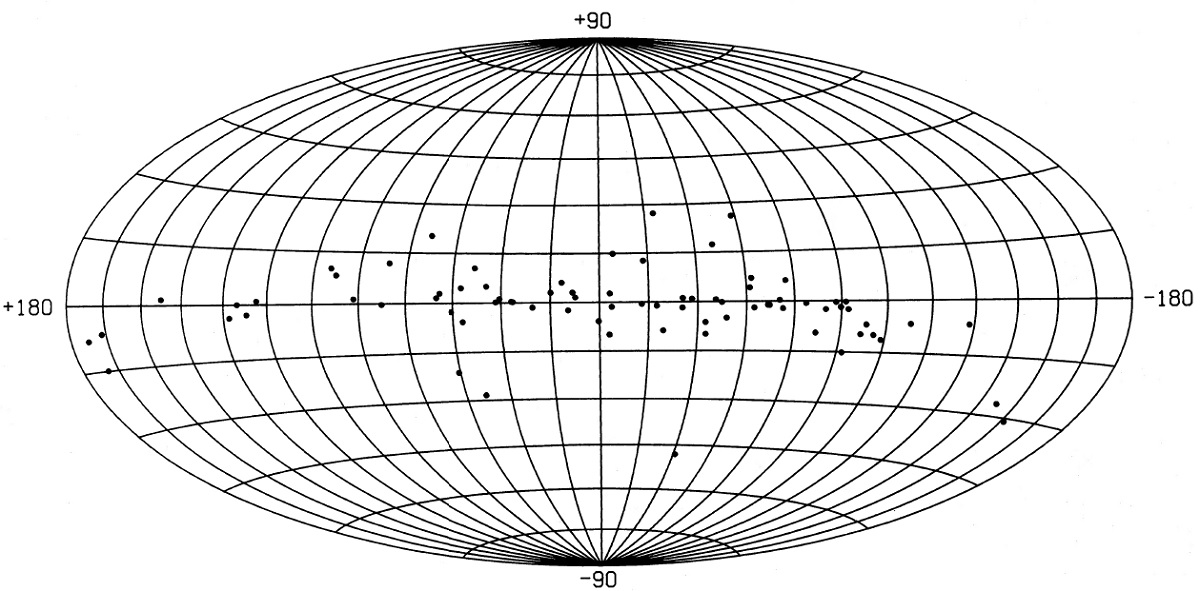
2.3. OH/IR 星との比較非変光 OH/IRs が LRS サンプルにない理由図3は IRAS と位置が一致した 100 OH/IR 星の二色図である。 幾つかは作業サンプルに含まれている。クラス30天体と良く重なっている ことが分かる。OH にはある程度厚いダスト層が必要であることを示している。 図1と図3の違いは、図3には log[(νFν)25/(νFν)12] > 0.1 かつ log[(νFν)60/(νFν)25] < 0, つまり、 F25/F12 >+log(12/25) > 0.42 かつ log(F60/F25) < 0.38 に、 多数の OH/IRs があるのに、図1にはないということ。これらの天体のカラーは Olnon, Baud, Habing, de Jong, Harris, Pottasch (1984) による 40 OH/IRs の IRAS カラーの研究では 非変光 OH/IRs のカラーに対応 する。それらは Bedijn (1987) により星周層が星から離れて行く post-AGB 星と解釈された。 もしそうならば、この時期は短期間と予想される。それが LRS サンプル中にこ のような星が見当たらない理由なのだろう。 (期間だけが理由か?) もっと赤い OH/IR 星 = HIIRs 図3にはさらに赤い log[(νFν)60/(νFν)25] > 0.2, つまり、 log(F60/F25) > 0.58 の OH/IRs がある。それらは Olnon, Baud, Habing, de Jong, Harris, Pottasch (1984) には現れない。そのカラー領域はクラス70天体と重なる。クラス70天体の 多くが HIIRs であり、図3の上部にある 9 OH/IRs の内 5 天体は HIIRs に 伴っている。残りの内の一つは OB アソシエイションに含まれる。最後に残った 3 天体は IRAS PSC には既知天体との随伴はない。しかしそれらのフラックス は低く、遠方天体なのかも知れない。このように、この非常に赤い天体たちは 星間ダスト起源と思われる。 その他 他には VY CMa のような He-core 燃焼期の赤色超巨星も OH/IR 星に混じっている。 また、25-60-100 二色図には OH/IRs が少ない、F100 の質が悪いため、使えない。 |
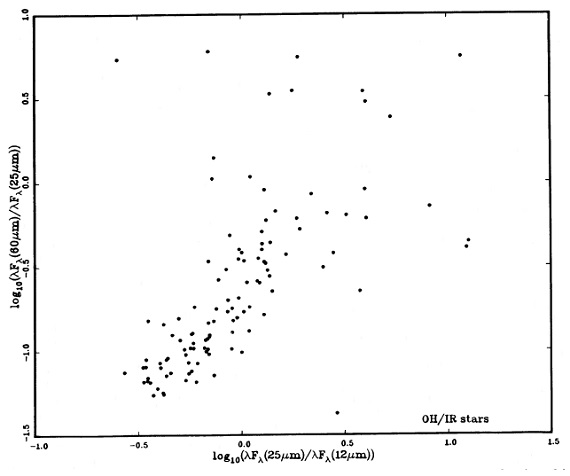 図3.OH/IR 星 100 個の IRAS 二色図。 log[(νFν)60/(νFν)25] = +0.2 が HIIRs との境界。 (前節の数字と違う ) |

2.4.超巨星作業サンプルには二つの赤色超巨星 VY CMa = IRAS 07209-2540 クラス 24 と VX Sgr IRAS 18050-2213 クラス 26 が含まれている。それらは OH/IRs 全 体の分布には影響しない。2.5.変光OH 変光Engels et al 1985, Herman, Habing (1985) の OH モニタリングは周期 2000 日にまで達する変光を検出した。しかし、中 には変光を示さないものもあり、AGB 期を終えたと考えられる。 IRAS 変光 IRAS の6か月置いた観測から変光度が算出された。クラス 25-29 で 75 % 以上、クラス 21-24 で 42 %、クラス 31-39 で 16 %, クラス 61-69 で 1 %, クラス 71-79 で 4 % である。進化がクラス20上部からクラス20下部、さ らにクラス30へと次第に光学的深さが厚くなる順に進むと仮定すると、光学 的に厚くなると変光度が低下すると解釈できる。 (そうか、前の方で 21-24 の 25/12 カラー平均が 25-29 より右と言っていたので変だなと思っていたが、著者たち は21-24 の方が 25-29 より厚いシェルと考えているんだ。驚いたな。) |
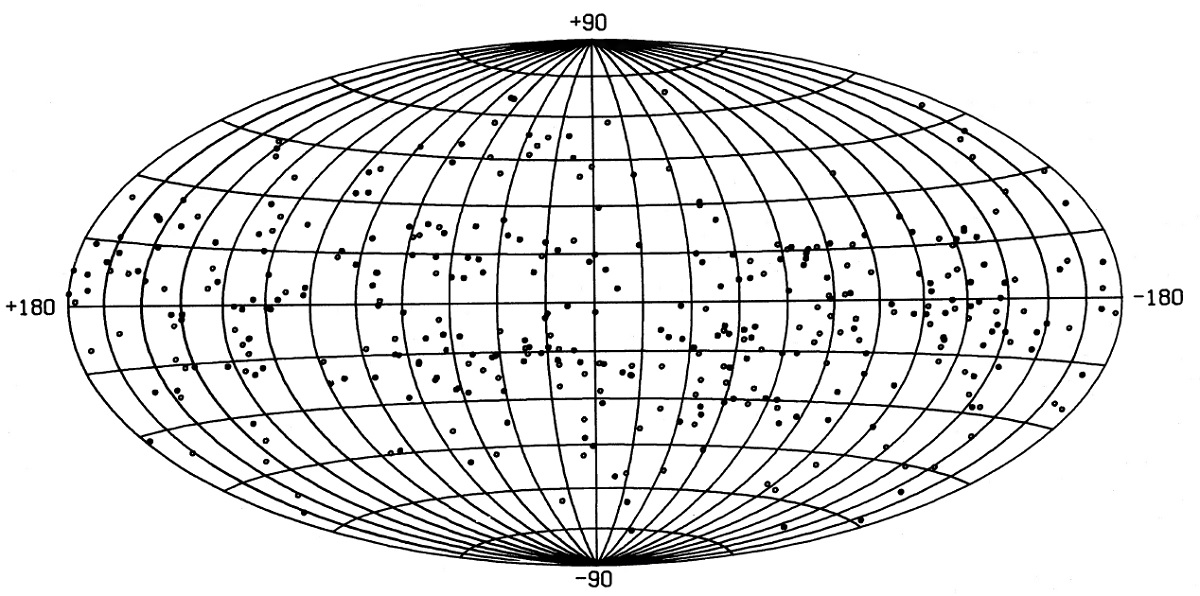
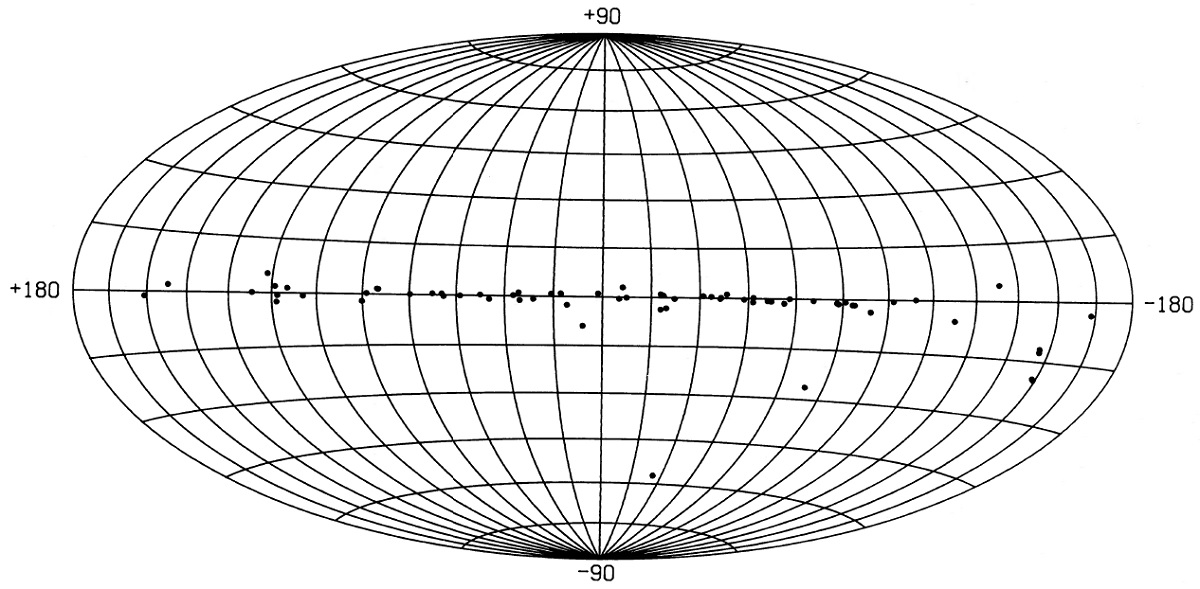
2.6.分布銀緯分布図4−7に作業サンプルの分布を示す。図4の分布は高銀緯にまで及んでいて、 クラス20天体がおそらく 2 kpc 以下の近距離天体であることを示唆する。 クラス30天体は銀河面により集中している。これは遠距離のせいか、または 高度スケール長が小さい高質量星であるためかのどちらかである。クラス70 天体は銀河面に最も密着しており、それらが HIIRs である傍証になっている。 バルジが見えない Habing85 は IRAS PSC の晩期星分布がはっきりしたバルジを現わすことを 示した。しかし、今回の LRSC 作業サンプルにはバルジが現れない。つまり LRS アトラスに載る星は比較的近傍の見かけ明るい天体なのである。 結論 クラス20天体は AGB 星であるが LRS クラスの一桁目ぼ数字が進化段階を 表すわけではない。クラス30天体はクラス20天体より進化が進んでいる。 しかし、それらには HIIRs が混じっている。恐らく log[(νFν)60/(νFν)25] > -0.3, つまり、 log(F60/F25) > 0.08 の 大部分は AGBs ではないであろう。 |
3.1.AGB 星の進化コアの進化L = 59250(Mc - 0.495) dMc/dt = L/xEH 上二式から、 dMc/dt = 8 10-7(Mc-0.495) Mo/yr これを解くと、 Mc(t) = Mc(0) + [Mc(0)-0.495][exp(t/to)-1] ここに、to = 1.2 Myr, Mc(0) = AGB 開始時のコアマス。 外層の進化 外層の進化はマスロスに影響される。適切なマスロス式を用いると Me(t)、 そして M(t) を計算できる。M(t) と L(t) から有効温度 T は Wood, Cahn (1977) にしたがい、 log T = [101.49 - 2.5log L + 0.533 M ]/26.64 で計算される。星半径 R は R(t) = {L(t)/[4πσT4(t)]}1/2 で与えられる。Ostlie,Cox,Cahn 1982 によると基本振動の周期は次の式である。 log P = -1.96 -0.67logM + 1.87logR |
3.2.星周層(dM/dt)t-r/V = 4πr2Vρ(r,t) ρ(r,t) = ρ(ro,t)ξ(r,t) τ=∫πa2QNd(r)dr 以上から、 (dM/dt)t-ro/V = C(F/ro)-1τ roV ここに、 C =(16π/3)(ρd/ψ)(a/Q), ρd = グレイン物質の密度、F=∫ξ(r,t)dr Nd = ψρ/md, (F/ro) = ∫[ρ(r)/ρ(ro)]dr/ro ここの計算をメモしておくと、 τ=πa2Q(ψ/md)∫ρ(r)dr =(3/4)(Q/a)(ψ/ρd)ρo∫&xi(r)dr ρo = τ(4a/3Q)(ρd/ψ)/∫&xi(r)dr dM/dt = 4πro2Vρo = 4πro2Vτ(4a/3Q)(ρo/ψ)/∫&xi(r)dr = (16π/3)(ρo)(a/Q)ro2V/∫&xi(r)dr 積分範囲が [ro,∞] なので、逆二乗密度則の時には、F/ro=1。また、 C はグレインのパラメターのみで決まる。 したがって、マスロス率は τ, ro, V で大体決まる。もっと言えば (τ/Q) だが。V, ro はあまり大きく動かないので、マスロスは大体 τ で決まると言える。 |
4.1. 計算法計算には Leung 1975 が開発した DUSTCD プログラム (Spagna,Leung 1983) ダスト凝縮温度 = 1500 K とした。4.2. ダストダストはシリケイト (Mg,Fe)2SiO4, ダスト/ガス比 = 4.3 10-3 と仮定した。 Q/a(9.7 μm) = 5.25 μm-1 である。すると、C = 1.090 10-3 Mo yr-1 pc-1 (km s-1)-1. 4.3. ダストオパシティ関数光学的深さの薄い星からのスペクトルにはオパシティ関数が直接に反映される。 18 μm 強度はよく分からないので 18/10 = 0.4 - 0.7 で考えた。LRS を見ると 18 強度は天体毎に異なる可能性もある。遠赤外ではλ-1 λ < 84 μm λ-2 λ ≥ 84 μm とした。図8に最終的なオパシティ関数を示す。 |
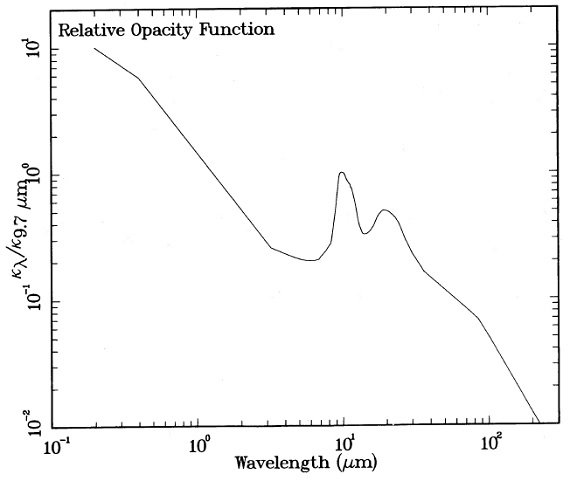 図8.採用したダストオパシティ関数 |
|
マスロス式 レイマーズの式は以下のようにあらわされる。 dM/dt = 4 10-13 η LR/M Mo/yr 根底の考えは光度の一定割合が星風の運動量に移り、星風の速度は星の脱出速 度に比例するというものである。この式は K-型、早期 M-型星の観測から導か れたので、AGB 星に直接適用可能かどうか不明である。η = 1 ではマスロ ス量が不足して、8 Mo の場合に AGB の終わりになってもまだ大きな外層質量 が残っている。 (外層マスが大きいのに AGB 終端になれるのか? ) その対症療法として「超星風」が仮定される。しかし、一本のマスロス式で最 終期の強いマスロスを表されればその方が良い。 改訂版レイマーズの式 8 Mo にレイマーズの式を当てはめ、 AGB 最終期に WD 最大マスになってい るようにしようと思ったら、$eta; = 4.5 が必要である。それより小さいと、 8 Mo 星が超新星になってしまう。一方低質量星にはもっと小さい η が 望ましい。両者を取り持つために η が初期質量に依存すると仮定する。 それは次の式で与えられる。 dM/dt = 1.8 10-12[Mms/8Mo] LR/M Mo/yr (外層マスが大きいのに AGB 終端になれるのか? ) (1 Mo で η=0.56, 8 Mo で η=4.5 に相当。もう少し書くと、18Mms/8=4η だから、 η = 0.56*Mms) マスロスによる進化 図9にマスロスによる進化を図示した。 (どうもマスロスが開始される先を AGBとしているようだ。本文は 1.5 Mo と 8 Mo を図に示すとか言ってる。 周期の式(9)はここには示さない。 ) |
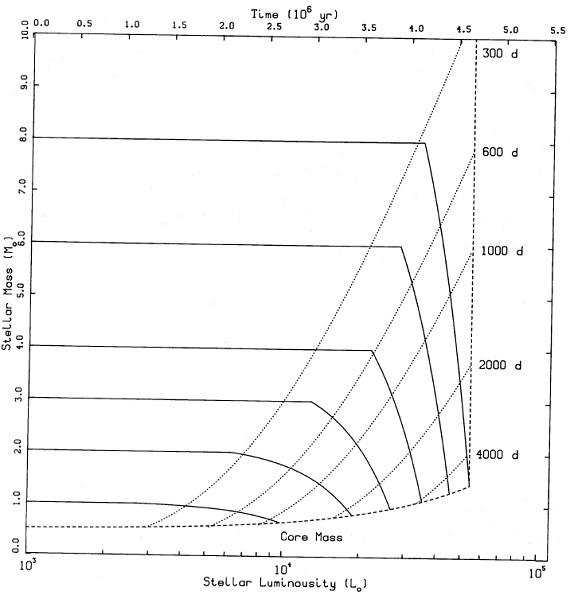 図9.採用したマスロス式での星質量-光度関係。点線=脈動周期一定。 (周期光度関係が無視されてる? ) |
 |
 |
 |
 |
 |
 |
 |
 |
|
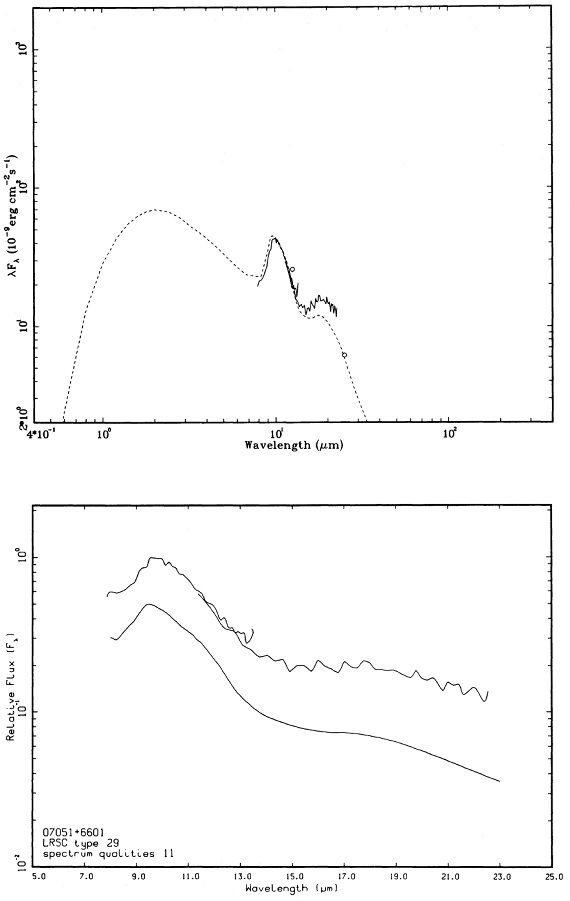
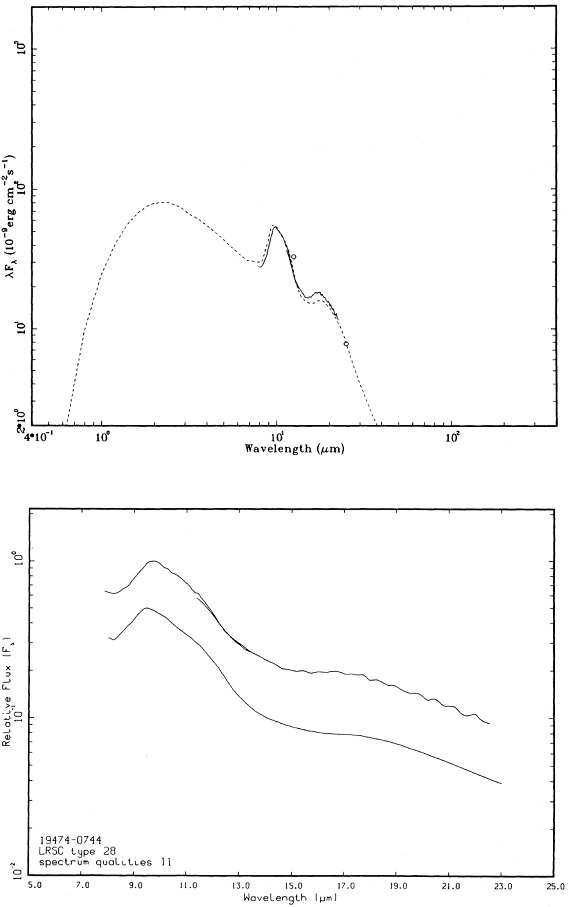
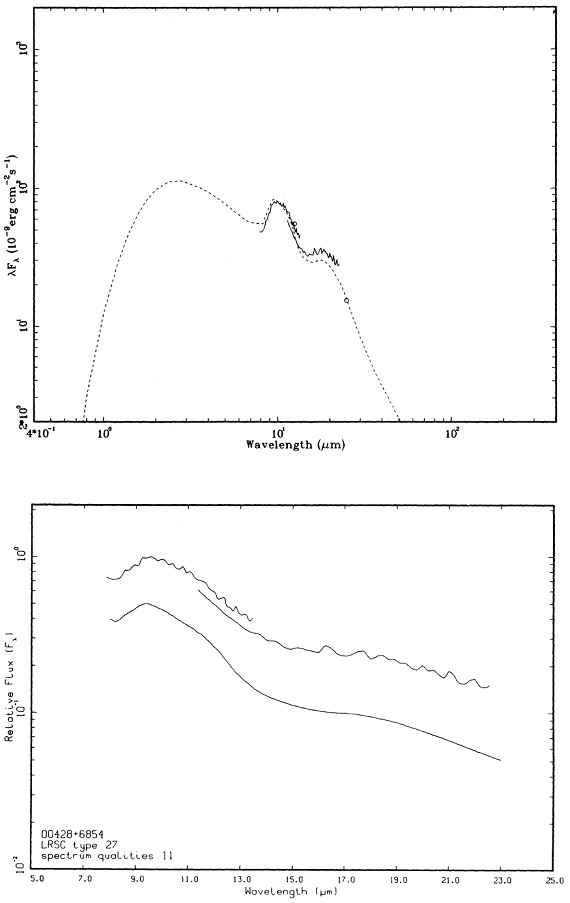
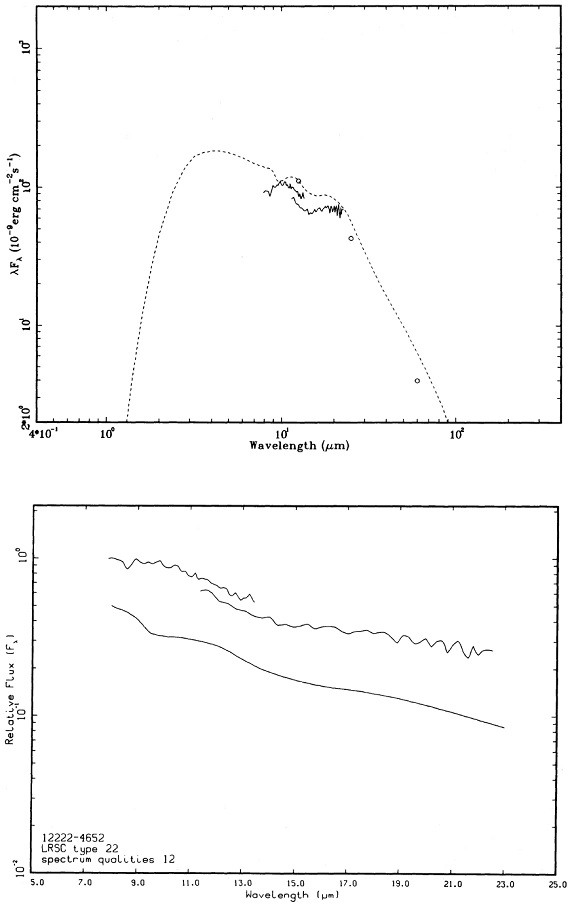
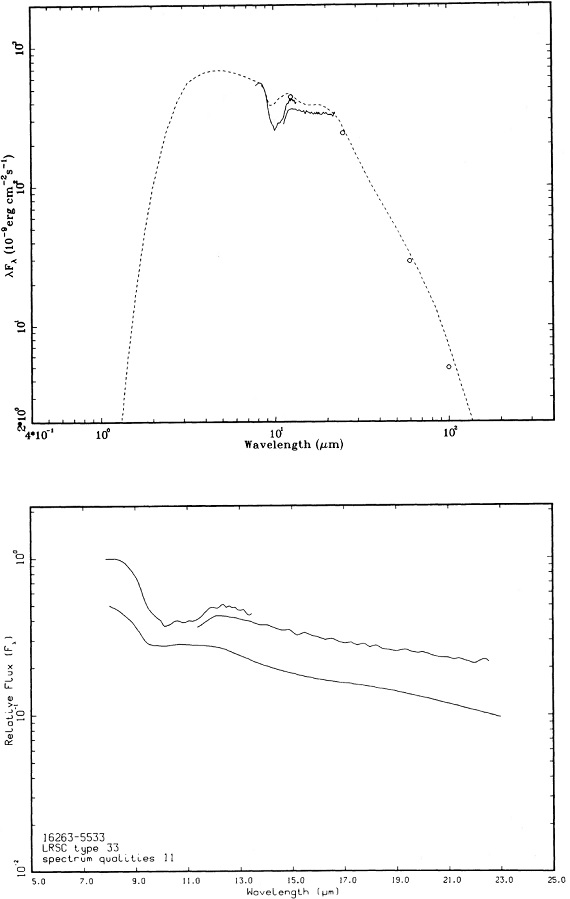
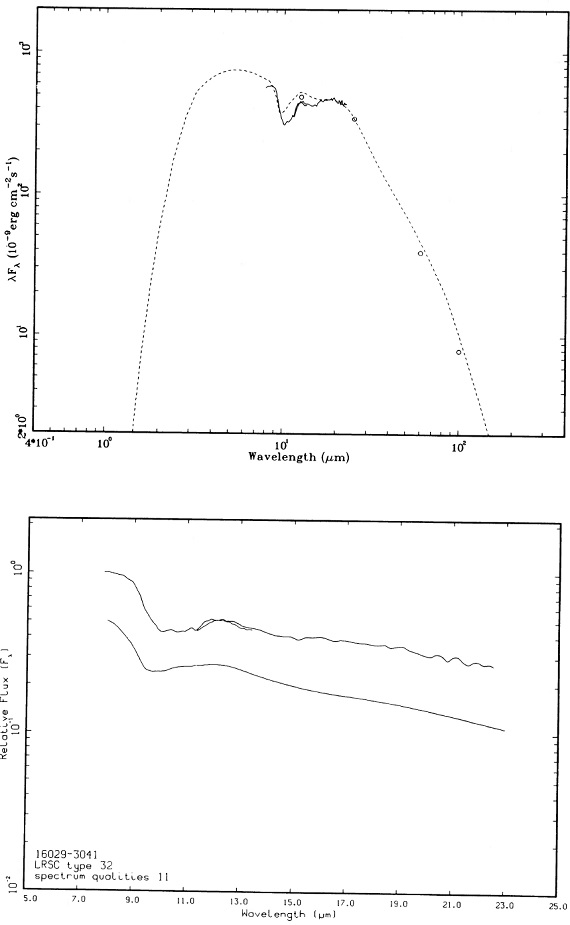
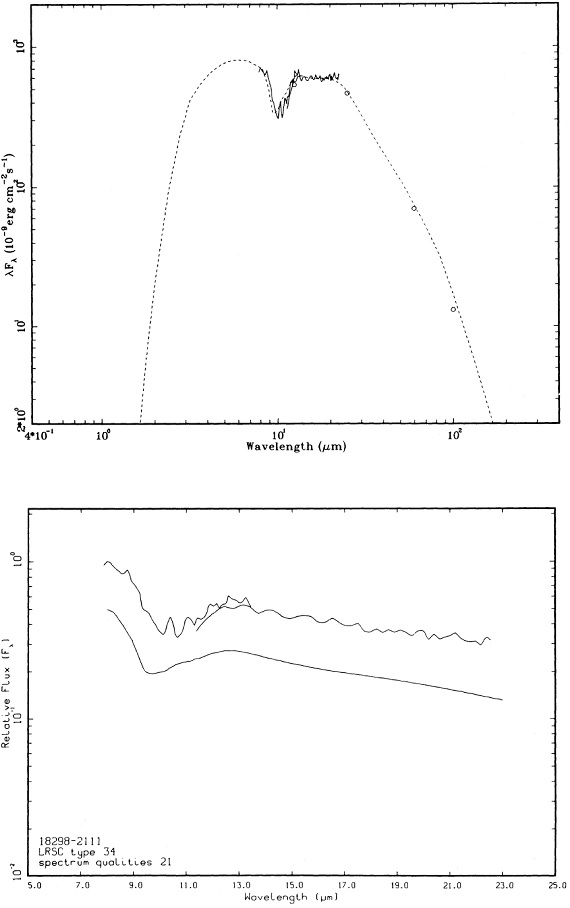
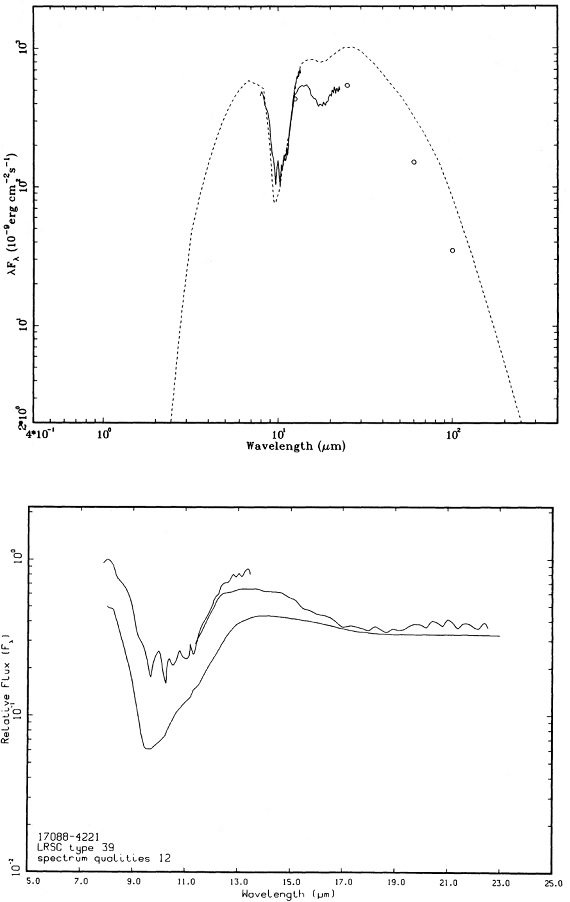
1.5 Mo 星のスペクトル進化 図10 a-d に1.5 Mo 星のスペクトル進化を示す。マスロス率は AGB 開始時 2 10-7 Mo/yr から 中心核が露出する 1.6 10-6 Mo/yr まで増加する。9.7 μm ピークでの最大光学的深さは 4 である。進化の 大部分の時期を通じて、シリケイト放射帯が見える。図の上はモデルスペクトル、下はそれに近い観測スペクトルを示す。 |
8 Mo 星のスペクトル進化 8 Mo 星に対する同様のスペクトル進化を図11 a-d に示す。この星の AGB 寿命は僅かに 5.22 105 年である。マスロス率は 6.7 10-6 Mo/yr から 中心核が露出する 9 10-5 Mo/yr までに及ぶ。光学深さは初めが 6.7 で最後は 49 である。この質量の星では シリケイトは AGB 期を通じて常に吸収帯である。 放射から吸収に シリケイト帯が放射から吸収に転ずるのは光学的深さが 4 の辺りである。 これは Jones, Merrill (1976) でも指摘されたことである。したがって、文献でしばしば使用されている ように、シェルの光学的厚みを s = -ln(F9.7/Fcont) で与えると、過小評価になる。 |
6.1.マスロス式今回使用したマスロス式は、唯一ではない。例えば、低質量星が最終期に非 常に高いマスロス星へと変貌し、短時間の間に IRAS 二色図を右へ移動し、吸 収帯スペクトルを示すことになるマスロス式もあり得る。そのようなマスロス 式では、図10に示される異なる初期質量の星の進化経路はもっと重なり合う だろう。年齢と初期質量の効果を分離するのは困難である。何故なら、初期質量が異 なる星が HR-図上の同一点を通過するからである。 (メタル量が同じなら、HR-図上で進 化経路は質量によりずれて行くのではないか?) 結果として、我々は使用したマスロス式の重要性を強調しようとは思わない。 しかし、経験的マスロス式の有効性を試す初めての試みである点は強調したい。 6.2.超星風超星風は Renzini83 が AGB 終末期に外層質量を下げるために仮定したもの である。我々のモデルでは AGB 進化の全期間でマスロスがレイマーズ式より 高く、したがって「超星風」の仮定は必要としない。マスロスが緩やかに増加 する方が実際に赤外、電波の観測に合う。(超星風があるかないか、観測から 決めることができる?あるかないかでどこが変わるのか?) マスロスが光度と共に上がることは確かであろうから、マスロス期の最後 104 年以下の時期を「超星風」と呼びたくなるかも知れない。 OH/IR 星を「超星風」星と呼ぶのは間違っている。なぜなら、可視対応天体の 見つからない AGB 晩期は 105 年以上続くからである。 (数字の根拠は?) 図10dに示すように、数X10-6 Mo/yr あれば星は完全に隠され るが、それくらいでは 「超」の名にふさわしくない。 |
6.3.星間減光Volk, Kwok 1987 は今回と同じサンプルを用いて、星間減光が吸収帯に影響 しないことを示した。簡単に言えば、3kpc程度の距離では中間赤外の減光は 強くないということである。IRAS 05307+4105 は星間減光が強い主系列星である が、青いために F100 が弱く今回のサンプルには含まれない。6.4.(?) OH/IR 星Baud85 はバルジ近くのシリケイト吸収を示す二つの OH/IR 星、 OH4.6-0.4 と OH0.2+0.0 の距離を 10 kpc と仮定して、その光度を 2.1 104, 0.2 104 Lo とした。 OH0.2+0.0 の低い光度はこの星が小質量 星であることを示唆する。これは、今回のモデルとは矛盾する。バルジ星が高 メタルであることが影響するのかも知れない。6.5.種族統計ここで示唆したように、シリケイト放射か吸収かは初期質量の差を示すもの ならば、観測される放射帯星の数は、放射期の長さとその質量範囲、初期質量 関数の積で予言できるはずである。我々は IMF ∝ M-2.35 を 仮定して、放射星数/吸収星数 = 2.7 とした。光度のバイアスも考慮した。(もう少し詳しく書いて欲しい。) 今回サンプルではクラス20/クラス30=7.5 である。計算に入る多くの 不定性を考慮すると、この程度の不一致は許容範囲であろう。 |
|
マスロス式とコアマス光度関係を仮定して星の進化を追い、それにシェルの
輻射輸達モデルを適用して、赤外スペクトルの進化を計算した。
τ = 4 で放射から吸収への転換が起きることが分かった。
最も厚い天体では τ 500 を超える。
(信じがたい!) | モデルから得られた進化経路は IRAS 二色図上での星の分布を再現する。 マスロス式はこれには限らないだろうが、観測との一致は驚くほどである。 したがって、今回の計算は、マスロス式を定量的にテストする初の試みと 言える。 |
|
進化計算の結果が時間軸で表現されていないので分かりにくい。 (a) 1.5 Mo の AGB 期間が 8 Mo より本当に短いのか、それともマスロス期 だけがそうなのか?(図12の理解) (b) 図12で実線(8Mo) はlog(F25/F12)= 0 から開始される。マスロス式では 8 Mo でもっと低マスロスの時期があると思うが。点線(1.5Mo) が突然折れ曲がる 理由は何か? (c) スペクトルは τ と ξ で決まるはずだが、8 Mo と 1.5Mo の同じ τ で比べた時、ξ の違いが二色図上の位置差を産み出しているのか?それは、マス ロス史の何を反映しているのか? |
(d) 少し意外なのは、著者が 21-24 天体は 25-29 天体より厚いと想定していること。
(e) 2.3.に述べられている非常に赤い Olnon84 リストにない OH/IRs が述べられている。 それらは自分/上塚の調査範囲にあるか? (f) 最大の主張は、8 Mo はマスロス最初から吸収で登場し、12/25/60 図の IRAS 帯の 上辺を動き、 1.5 Moは最後まで放射で二色図の下辺をかすめる。あと、超星風は要ら ないというのもかな? |