Miras Variables, Mass Loss, and the Fate of Red Giant Stars

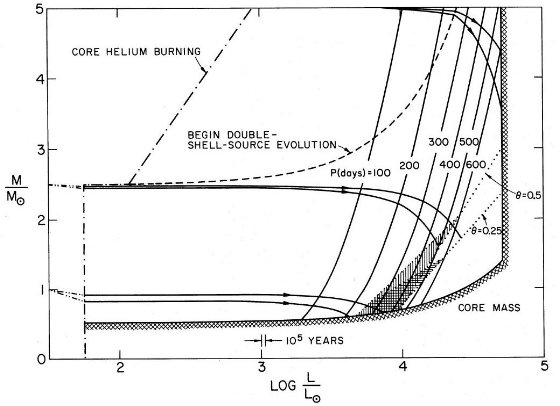
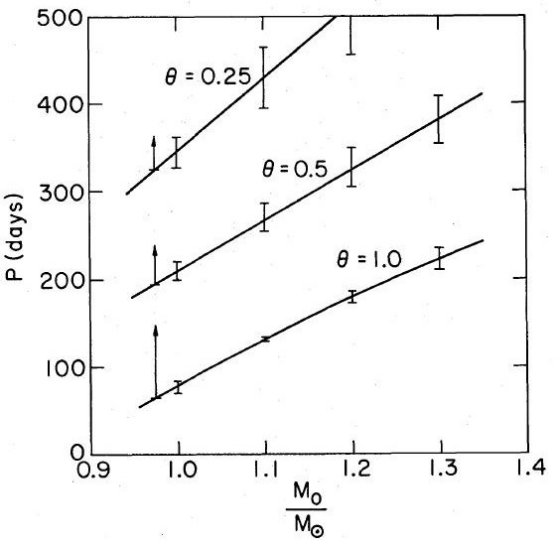
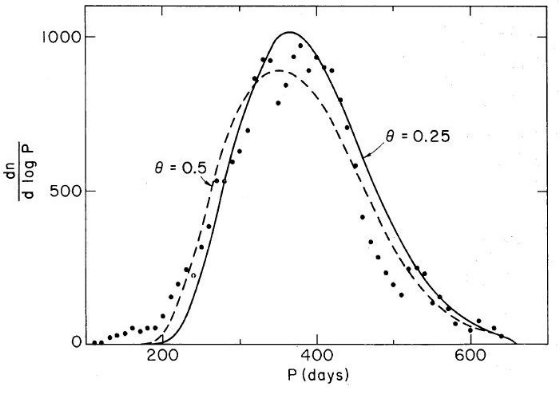
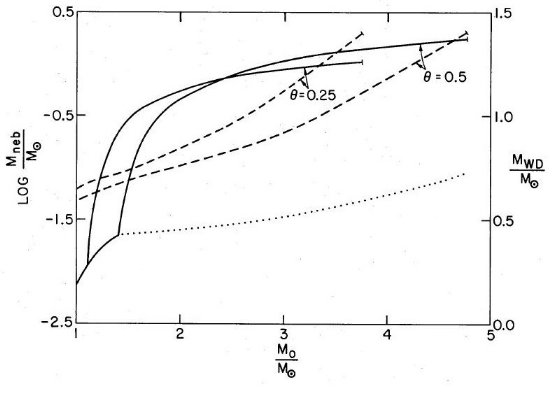
２．観測による周期分布　 ミラの絶対等級　 　データはストラスブルグ天文台のCDSから得られた。そこには、22,650 星の 変光データを含むGCVSが含まれる。4758 星がミラ型と分類されている。 M型、S型ミラ　　 　P ≥ 175 日のミラ型星までの距離は Clayton, Feast 1969 による 統計視差の結果を用いた。P < 175 日のミラ型星 (全体の 2.5 %) までの距離は、 極大光度 = 一定と仮定して求めた。Clayton, Feast は 。P < 175 日 で光度 が鋭く落ち込むことを見出した。しかし、 Eggen 1975 が見出した P < 150 日ミラ 4 つのミラ型星に対するデータからの(MI R - I) 関係に基づいている。その結果は極大時に　Mv = -3.0 ± 0.5 である。 C型ミラ　　 　炭素ミラ(∼ 6.7 %) では、Gordon 1968 が N-タイプ炭素星に対し、Mv = -3.0 を得ている。炭素星は赤いので Mpg - Mv = 3.5 を　Mendoza 1967 から 決めた。この補正を行うと、炭素星の Mpg は P ≥ 350 日の M, S 型 星と同じくらいになる。 GCVSへの補正　　 　GCVS は極大等級を与えているので、平均等級を出すため 0.75 等の補正を加えた。 この補正値は Clayton,Feast のサンプルの値 0.75 ± 0.35 等に基づいている。 Mendoza によると、M, S 型では、極大時に B - V ≈ 1.6 であり、一方 Allen 1973 は B = mpg + 0.11 としている。これらから、Mpg - Mv = 1.5 となる。Pが与えられていないミラは P = 320 d ミラ の等級とした。星間吸収は Cahn 1976 の銀河系吸収モデルに従った。そこでは、PN の 電波と Hβ フラックスから決めた Hβ 付近での減光を用い、 FitzGerald 1968 のカラーエクセスモデルを銀河系減光モデルに変換している。 ミラの距離　　 　太陽からの距離 R と銀河内での位置がこうして計算し、|Z| < 2 kpc のミラ を選んだ。R 以内の星の数 N(R) を R2 に対して求め、銀経の各象限毎に プロットしたのが図１である。R ≤ 1.7 kpc までは直線状に変化しており、サンプル の完全性がその辺りまでであることを示唆している。 象限毎の密度分布の特徴　　 　R = 0.6 - 0.8 kpc での密度分布を見ると、第2(90° ≤ l ≤ &180°) と 第4(270° ≤ l ≤ &360°)象限が高いことが分かる。両者は銀河系の 局所腕のために密度が上がっているのであろう。 腕部で星の密度増加は 5 % くらいと思っていたが、こんなに 大きいのか？腕の巾を考えると腕部分での増幅はもっと大きい。ミラは高齢と考えると ホントかな？周期毎の立体分布は出せたら面白いだろうな。 この密度の高まりは過去に晩期型 巨星のサーベイで Mavridis 1971 が見出した銀河面での密度変化に対応している。 象限毎の密度分布の特徴　　 　われわれは、R < 1.5 kpc, |Z| < 0.2 kpc のミラを全て取り上げた。これは 赤化なしの限界等級として、mpgLim = 11.2, mvis Lim = 9.7 に相当する。M, S 型ミラとしては P = 300 d である。この （完全）サンプルは全部で５１１星でその内４７８星は周期が知られている。その 内訳は、266 M + 21 S + 21 C + 170 スペクトル型不明　である。残りの３３星は 周期不明である。 R < 1.5 kpc のミラを銀河面距離 Z に対してプロットして密度 n(Z) の変化を調 べると、面のどちら側も dn = 245 exp (-3.18|Z|) kpc-4 dZ 　図２には dn/dlogP を P に対して 10 日おきにプロットした。 n の引数がめちゃめちゃなようだが　カーブを滑らかにするため 3点ランニング平均が使われている。カーブは総数密度が 245 ミラ kpc-3 となるよう規格化してある。図2の表記だと面積を求める のは間違い。ついていけないな。

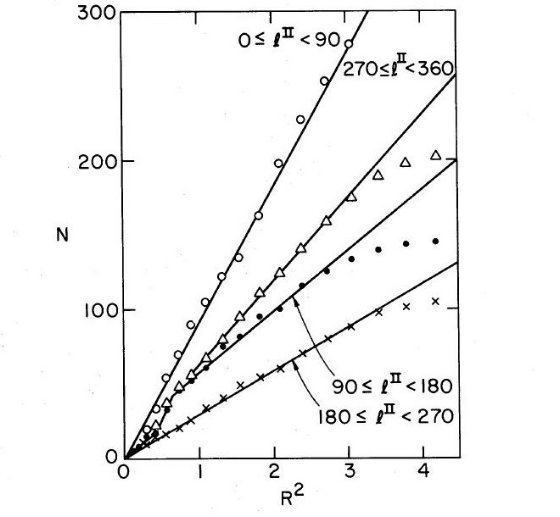
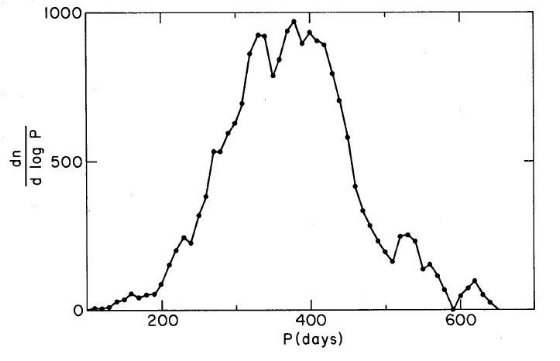
図１　|Z| < 0.2 kpc のミラの累積数 N の R2 に対する変化。 　　　各象限毎にプロットした。第2、第4象限が大きい。R < 1.7 kpc (R2 < 2.9) 　　　までは直線変化でデータが完全であることを示唆している。 図２　n(P) = 周期 < P のミラの空間密度(kpc-3)として、 dn/dlogP を P に 　　　対してプロットした。横軸がlogPでないので注意。

　４．詳しいモデル：ミラ不安定帯　

光度と振動モード　 　理論 (Keeley 1970, Smith,Rose 1972, Wood 1974, Stry 1975)と観測(Wood 1975) は 星が巨星枝を上がるに連れ、高次倍音振動で小振幅の赤色変光星から、次数を減らして 行き第1倍音のミラになることを示している。より明るくなると基本振動が始まる。 Paczynski,Ziolkowski 1968 は線形断熱振動の計算 から、緩和振動が起きかつその発生光度は星質量が大きいほど高くなることを示した。 Wood 1975 は非線形非断熱振動の計算から力学的不安定性について同様の結果を得た。 したがって、質量ー光度平面上にミラの第一倍音不安定帯を描くとその勾配は正で ある。観測される (dn/dlogP, P)図はこの (M, L) 面上での星の進化経路と不安定帯 の位置に依存する。以下ではこの方針で調べて行く。 進化の式　 巨星枝　 　ミラは巨星枝上にあると仮定する： 　　　　　Mbol = 26.64 log Te - 0.533 M - 96.34 + Δ　　　(6) この式は M = 1, Δ = 0 で (2) 式と同じである。 (6) 式の質量依存性は Mc, L, (l/H) 一定の理論モデルで M を変えた時に Te に出る変化を粗く近似したもの である。 Δ は Te,L の分散を示す。 マスロス　 　マスロスにはレイマースの式を仮定した： 　　 dM = -4 × 10-13 η L R M๏ yr-1 　　　　(7) dt M 　第1巨星枝では M < 2.5 M๏ に対し (7) 式を適用した。Rood 1972, Faulkner, Cannon 1973 にしたがって RGB 先端光度を log L = 3.3 とし、 進化率を彼らの論文からとった。ただし、Rood の解析解はマスロスを考える場合は 不適当である。 RGB では　Mc - L 関係が使えないから AGB ではマスロスを考える。 光度変化　 ヘリウム核燃焼の後、ヘリウム燃焼殻が水素シェルに 近づいて行く過程では、進化の式は　Eggleton 1973 の 4 M๏ 進化 の計算から：これを Mc に直せば AGB 下部の Mc - L 関係か？ 　　 　　 dMbol = -2.97 × 10-6 mag yr-1　　　　　(8) dt

図３　下のハッチ線は Paczynski の Mc - L 関係。右の縦ハッチ線は縮退核の限界 光度。一点鎖線はヘリウム核燃焼光度ー星質量関係。鎖線はヘリウム核燃焼終了後 に始まる水素殻燃焼の再開。ミラの周期＝一定線は数字（周期）付き実線。矢印 付きの2本線組は下から 1, 2.5, 5 M๏ の η = 0.25 と 0.5 の進化。点線で区切られた影線領域は η = 0.25 と 0.5 のそれぞれに 対応するミラ不安定帯。不安定帯右側の大規模質量放出による縁線はもっと明るい 　L　の方に外挿されている。 　仮定したヘリウム核燃焼光度と、ヘリウム殻燃焼が水素殻燃焼にいつ追いつくかは 図3に星質量の関数として示されている。類似の計算は、Fusi-Pecci,Renzuni 1976, Scalo 1976 でなされている。 　以上の仮定の下で、質量ー光度平面上での進化が計算された。図3には M = 1, 2.5, 5 M๏ に対し、η = 0.25, 0.5 で計算した6本の進化 経路が描かれている。Paczynski 1971 の Mc - L 関係も描いてある。 RGB と AGB の進化の両方を計算して図3に書き込んであるのか？ 式（８）は 5 M๏ のヘリウム核燃焼とダブルシェル燃焼の間に 使い、ダブル燃焼後（1, 2.5 M๏ では殆ど）は式（１）を使うので はないか？ RC 期が見当たらないのは変だ。

主系列星終了率　 　光度関数に McCuskey 1966 の表8を用い、それに表12の補正を行い、 主系列光度関数を得た。縦方向の密度はミラの分布をフィットして exp(-3.18/|Z|) とした。 　星形成率の時間変化に Tinsley 1974 の exp(-t/τ), τ = 5 × 109 年、を仮定して、Iben 1967 の主系列寿命と、銀河年令= 10 Gyr を一緒に合わせると、銀河面で主系列星の年齢構成まで 込みで実の数分布を与えているということか？いや、IMF または ILF を与えて いないのにそんなことができるのか？計算の内実が飛ばされている。 現在の主系列星の終了率が出る。 η の推定　 　観測（dn.dlogP, P) カーブを再現するため、適当な η の値を高速度ミラと ハローミラを使って探してみる。図4には η = 1.0, 0.5, 0.25 のそれぞれ について、外層が消散する前に到達する最長周期をプロットした。エラーバーの 大きさから分かるように、最長周期の大きさはAGBの位置を0.5等上下したくらい では動かない。しかし、ヘリウムフラッシュの光度はかなり大きい影響を及ぼす。 　高速度星ミラは P ≤ 300 d, 球状星団のミラは P ∼ 200 d (Feast 1972)である。 もっとも　Andrews et al 1974 はもっと長いミラ候補を上げている。これらの星の Minit ≤ 1 M๏ なので、図4から η ≤ 0.5 が必要 である。同様に、高速度ミラに P > 300 d が見られないので η ≈ 0.25 が η の下限であろう。こうして、0.25 ≤ η ≤ 0.5 が得られた。 メタルの効果はどこへ行った？ ミラ不安定帯　 　次に、ミラ不安定帯がどこにあるかを探そう。まず、我々は不安定帯は M-logL 面内 で直線で囲まれていると仮定する。その底辺はある質量の星がミラになるのに必要な 最低光度である。上辺はマスの急速放出でミラが停止する光度を表わす。 　P <: 300d の周期分布を再現するには、M ≈ 1 M๏ の 星で P ∼ 250 d に相当する光度でミラ開始となる必要があることを見出した。 また、 P ∼ 420 d に相当する光度でミラ終了となる必要がある。試行錯誤の 結果、平行線のミラ帯では長周期(P > 450 d)ミラを作りすぎることが分かった。 頂点が P = 600 d にある三角形が最適であることが分かった。あとは三角形の 傾きである。傾きが緩すぎると不安定帯は周期一定線とほぼ平行となってしまい、 周期分布が鋭くなり過ぎる。逆に、勾配が立つと周期分布の巾が広くなり過ぎる。 　結局、dlog L/dM ∼ 0.5 - 1.0 あたりが適当である。図3の楔形不安定領域 は η = 0.5, 0.25 の最適解である。　図5はその結果の dn/dlogP を示した。 どちらも、急速放出のラインは高光度側に超新星リミット(Mc = 1.4)まで外挿した。 この外挿線の意味は質量が大きくなると、第1倍音でミラになる前に急速放出光度 に達してしまうということである。 熱パルスによる間歇的放出　 　まだ論じていない現象は熱パルスである。この時、非常に短い増光の後、星は log L で 0.2 くらい暗くなる。注意すべきはこの大きさがミラ不安定帯の巾より 大きいという点である。このため、星はミラ不安定帯に入っても一部の時間しか 不安定帯に滞在しない。多重シェル惑星状星雲は急速放出期の縁付近でこの 熱パルスによる間歇的放出を経験したミラによるものであろう。

図４　AGB 上での最長到達周期。η = 1.0, 0.5, 0.25 に対し計算。 　　　エラーバーは巨星枝等級を 0.5 等上げ下げした時の変化。 　　　RGB 先端でのヘリウムフラッシュ強度を半分にした時の変化が矢印。 図５　図2と同じ観測周期分布に η = 0.5, 0.25 モデルによる分布を重ねた。。

　５．モデルから導かれること　

(a) AGB 進化の中断　 　モデルから、AGB が終了するのに３つの型があることがわかった： （１） Minit ≤ 1.4 M๏ (η = 0.5) か Minit ≤ 1.1 M๏ (η = 0.25) 　　　星風のみで水素外層を消散させてしまう。 （２）1.4M๏≤Minit ≤4.7M๏(η=0.5) か1.1M๏≤Minit ≤3.7M๏(η=0.25) 　　　　一部が星風で放出され、不安定になって残りを一気に放出する。 （３）　4.7 M๏ ≤ Minit (η = 0.5) か、 3.7 M๏ ≤ Minit (η = 0.25) 　　　　外層が失われる前に核が　1.4 M๏ に達し、超新星になる。 　(b) 惑星状星雲と中心星の質量　 　図6に惑星状星雲と中心星の質量が初期質量 Mo によりどう変化するかを示した。 星雲マスには最終放出前 　2 × 104 年続いた時の寄与分を加えた。 2万年分の星雲ガスは見えるからである。しかし、大抵の場合無視できる。

図６　モデルMi - Mf 関係。Mo = Minit, 実線＝Mneb = PN マス（左軸） 　　　　鎖線＝MWD = WD 又は PN 中心星マス(右軸)。点線は通常星風が 　　　　PN 放出前　2 × 104 年続いた時の寄与分。

(c) 惑星状星雲と中心星の質量の分布　図７，８ 　図6の結果を使い、主系列星の終了率を合わせると、二つの質量の分布関数が得られる。 図7を見ると、惑星状星雲中心星の分布が 0.6 - 0.8 M๏ で鋭く尖って いることが分かる。銀河面から離れ、大質量の星が少なくなるとこの傾向は一層 強まる。惑星状星雲質量は図８にあるように双頂型である。低質量側の山は星風のみ で生まれたもの、高質量側は急速放出によるものである。後者は銀河面から離れると 少なくなってくる。 図７　χPNN = 質量が MPNN 以下の惑星状星雲中心星の 誕生率 (yr-1kpc-3) 　　　θ = 文中のηのこと。　1.5M๏マーク＝初期質量1.5の 位置。

ミラの Z 方向分布はスケールハイト＝0.3 kpc であった。これは、惑星状星雲で 0.1 kpc (Cahn,Wyatt 1976) よりずっと大きい。銀河面から離れると、惑星状星雲 がミラに較べ急速に落ちて行くのは、低質量星雲の数が増えるためだろう。それらは 表面密度が低いため検出しにくい。これ、モデル分布のはなし だったんじゃないのか？これに検出率と寿命の調整をして観測と比較される分布 になる。 図８　χneb = 質量が Mneb 以下の惑星状星雲の 誕生率 (yr-1kpc-3) 1.5M๏マーク＝初期質量1.5の位置。

(d) 白色矮星の質量分布　図９ 　惑星状星雲中心星の質量分布は明るく若い白色矮星の質量分布のよい近似となる。 しかし、白色矮星全体は銀河系の星形成史を反映している。初期質量関数(IMF)と 星形成率の時間変化を用い、図９にあるWD分布が導かれた。この分布から導かれる WD平均質量、0.92M๏(η = 0.25), 0.83M๏ (η = 0.5), は観測からの平均値 0.5 - 0.9 M๏ とよく合う。 　(e) 数密度と終了率　 　白色矮星は M < 3.7 M๏ (η = 0.25), M < 4.7 M๏ (η = 0.5), から生まれ、WD　の総終了率 （？）として、 2.5 × 10-3 yr-1kpc-3 (η = 0.25), 2.7 × 10-3 yr-1kpc-3 (η = 0.5),を 与える。これを銀河系の歴史全体で積分して、0.055 pc-3 (η = 0.25), 0.057 pc-3 (η = 0.5), を得る。この値は観測されるWDの 終了率, 1 - 5 × 10-3 yr-1kpc-3 Weidemann 1968、惑星状星雲の終了率 3.2 × 10-3 yr-1kpc-3 (Cahn,Kaler 1971), 4 - 6 × 10-3 yr-1kpc-3 (Cahn,Wyatt 1976) と合致する。これは又、枠色矮星の総密度 0.005 - 0.048 pc-3 (Weidemann 1968) とも合う。 　ミラの終了率は 1.6 × 10-3 yr-1kpc-3 (η = 0.25), 2.2 × 10-3 yr-1kpc-3 (η = 0.5),で WD, PN のそれより低いが、低質量星が星風のためミラに ならないからであろう。ミラになるのは、1.0 - 2.1 M๏ (η = 0.25), 1.05 - 3.1 M๏ (η = 0.5), である。

図９ nWD = MWD以下の白色矮星の数密度(pc-3)。

　６．まとめ