|
モデル 球対称ダストシェルモデルを、現実的なグレインオパシティを 用いて計算した。結果をグラフで表示した。 シリケイト吸収帯 シリケイトグレイだけのシェルでは Tdust < 250 K の 光学的深さが十分に大きい時にのみ 10 μm 吸収帯が現れる。 この条件は他の種類の温かいダストが共存する場合には緩和される。 |
”ダーティ”で短波長輻射を効果的に吸収するシリケイトが 混在するモデルと”純粋な”シリケイトが他のより吸収的なダスト に混ざっている場合との間にはっきりした区別がある。後者の場合 にはダスト種毎に温度を計算しなければならない。 ダーティシリケイト 地球上のシリケイトと比べ、星周ダストは 1 μm ≤ λ ≤ 5 μm で吸収率が高いらしい。 |
 図１．観測赤外スペクトル |
３．１．輸達モデル波長帯を表1のように１７波長に分ける。輻射＝星からの減光された輻射＋ 周囲からの輻射（星の散乱光＋シェルの熱輻射）。周囲からの輻射はエディントン 近似で扱う。つまり、輻射場をルジャンドル展開した時の等方項と、線形項しか 考えない。計算法は付録Ａに記述した。３．２．輻射平衡ダスト温度は次式で決まる。 ここに、J はダスト位置での平均輻射場であり、エディントン近似の初項にあたる。 この温度を３．１．の式に入れ、逐次的に J と T を決めて行く。 ３．３．グレインパラメタ―炭素ダストSiC は 12 μm の狭い波長域以外では効かないと判断し、 今回は無視した。λ = 0.3 - 30 μm では Taft,Philipp 1965 の光学定数を用い a = 0.05 μm ミー計算を行った。 その先は Q ∝ λ-2 を仮定した。 |
|
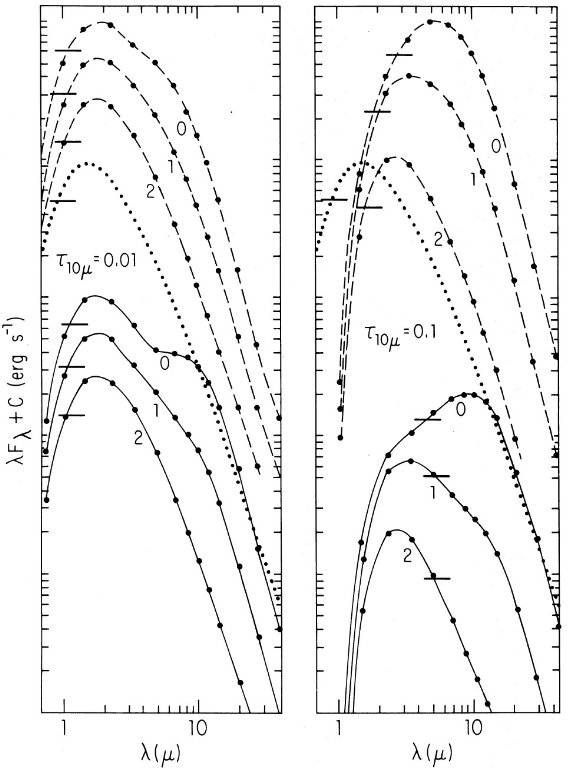
シリケイトダストの中間、遠赤外吸収（ λ >
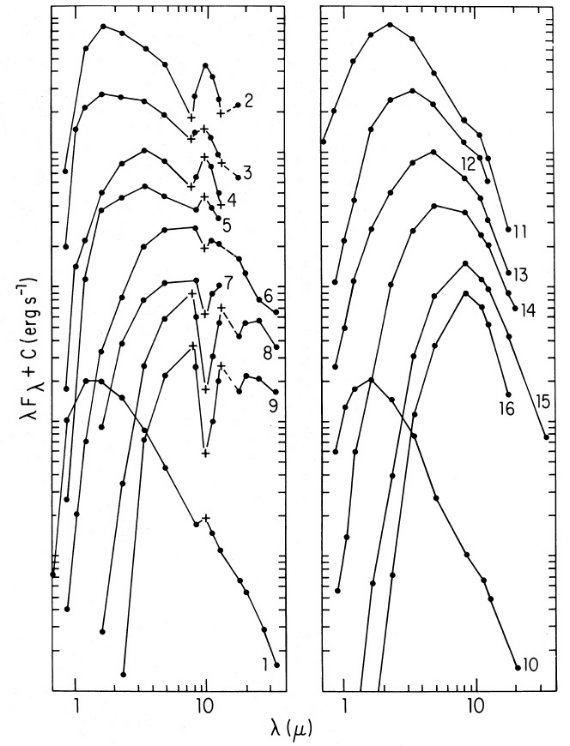
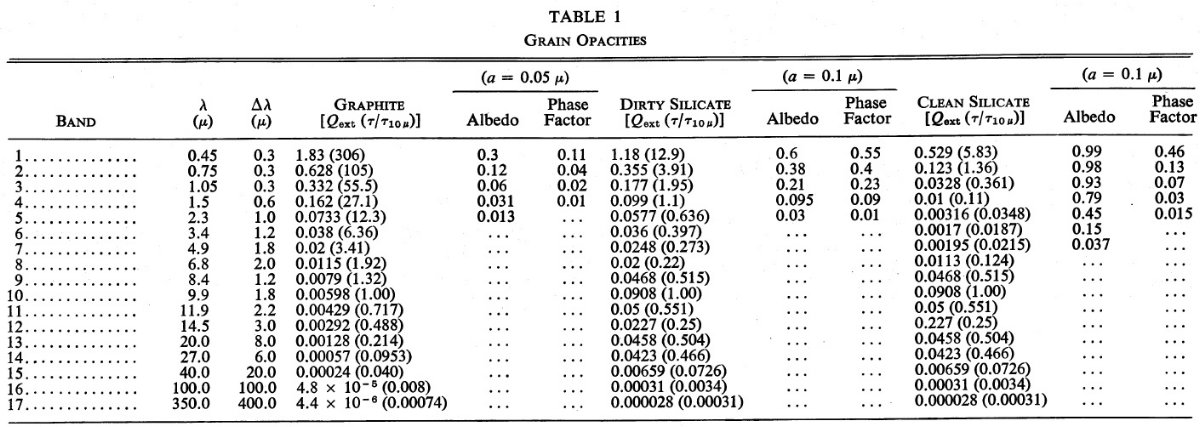
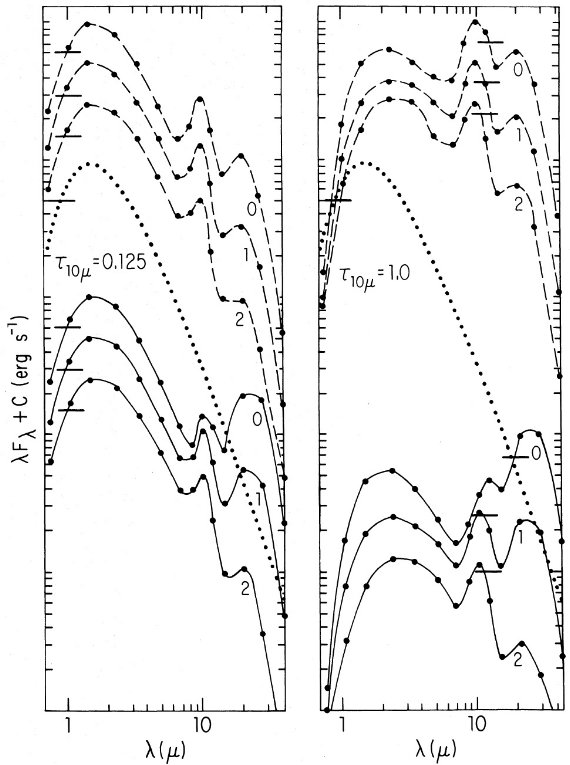
8 μm ） 地上鉱物の光学定数から期待される放射、吸収帯に較べると、 天体の 10, 20 μm 帯は滑らかで、かつ互いによく似ている。 そこで、 Gillett, Forrest et al 1975 に倣い、トラペジウムの放射を ２５０Ｋ温度で較正して、10 μm 放射帯の形に使用した。その強度については、 10 μm 吸収バンドは積分強度を地上シリケイト Pollack, Toon, Khare (1973) と同じにし、 22 μm 吸収バンドはその 0.7 倍強度とした。 λ > 50 μm では Q ∝ λ-2 を仮定した。 クリーンシリケイト λ < 8 μm では二つのはっきり異なるモデルを較べた。 モデル１：玄武岩の光学定数（ Pollack, Toon, Khare (1973) を使用。λ = 1 - 5 μm ではかなり透明。それで、"クリーンシリケイト" と呼ぶ。 この波長帯は星のフラックスが集中するので、"クリーンシリケイトダスト" は 星近くでも低温のままである。そのため、τ(10μm) >> 1 にならないと、星のフラックスは十分に吸収されない。 これでは観測されるスペクトルを再現できない。 |
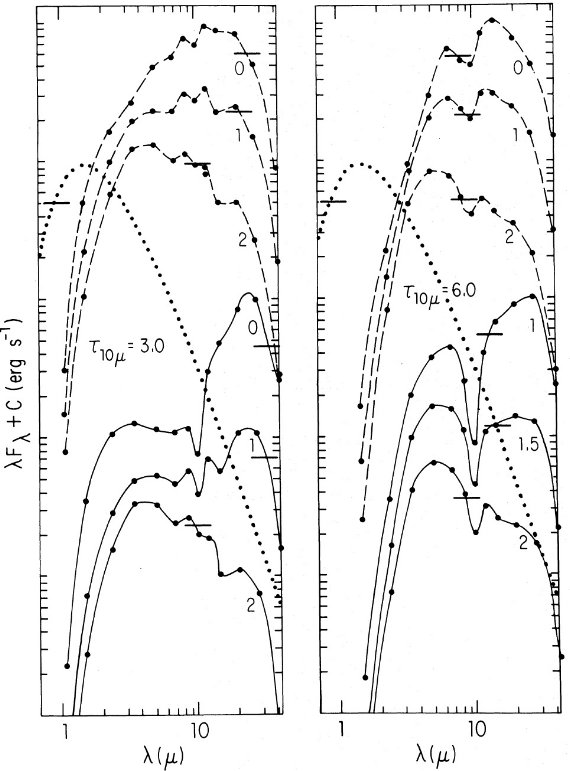
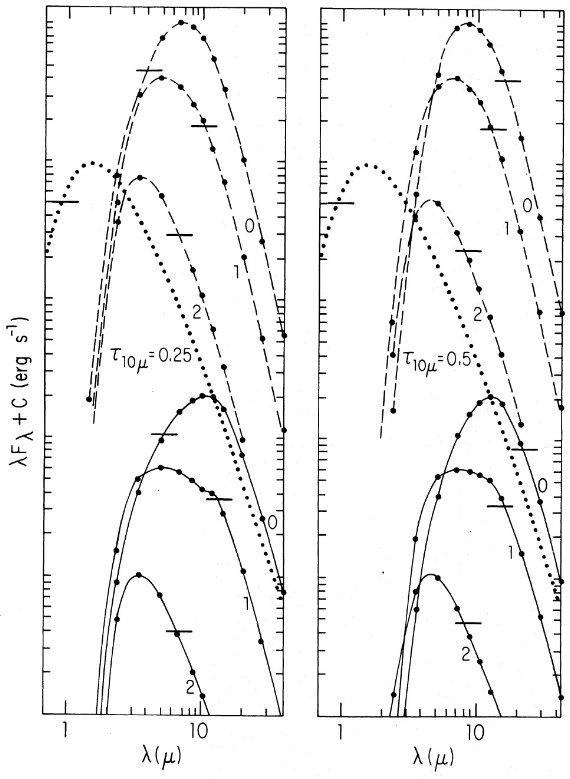
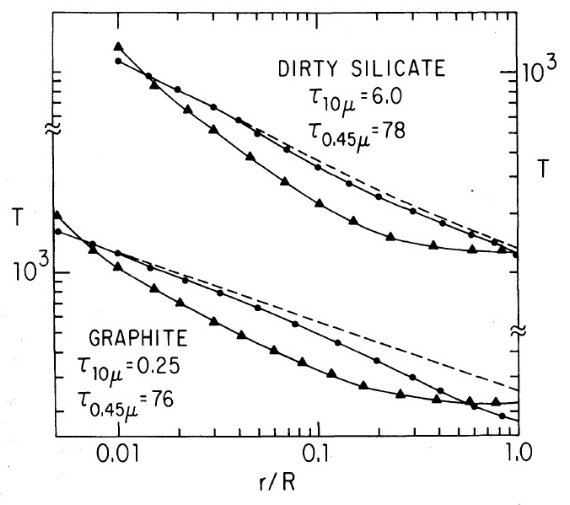
ダーティシリケイト モデル２： それで、近赤外領域で光を吸収する "ダーティシリケイト" を仮定する。 この物質は λ < 8 μm で m = 1.55 - 0.1 i を示す。これは隕石 のマトリックス物質の光学定数 (Dorschner 1968, Dorschner (1971) ) に近い。今回はこちら を用いた。表１にはこの仮想的光学定数も載せた。このモデルを使うと星の観測 を上手く説明できた。さらに興味深いことに、この吸収係数は VI Cyg No.12 の 減光曲線ともよく一致した。 クリーンシリケイトと他の物質との混合 "ダーティシリケイト" の別案として、"クリーンシリケイト" グレインと グラファイトグレインの混合を考えた。後でもう少し詳しく述べるが、この ような混合モデルのオパシティを "ダーティシリケイト" のオパシティと一致させても、 結果として得られるスペクトルは著しく異なることが判った。 |
|
ホモロジー 球対称を仮定すると、付録に示すように、輻射輸達の式の解に必要とする パラメタ―は少ない。例えば、L* と R = シェルの外側半径を独立に決める 必要はない。輻射輸達の式の解はフラックスと似たパラメタ― Fs = L*/R2 = 4πσTe4(r*/R)2 で 特定される。しかし、後に見るように、Ri/R を決める必要がある。 このパラメタ―化は特に有用である。と言うのは、観測的にはフラックス Fo と 視角 θ が得られるからである。観測した視角は規格化半径 ρ= r/R と 次の式で繋がれる。 ρ = θ(Fs/4πF)1/2 こうして、天体距離や光度が分からなくとも、モデルと天体とを比較することが 可能となる。 (これは、見かけ広がりが見える場合の 話しなのか？確かに、その時は Fs と θ が分かる。モデルは Fs と θ の指定で作れるのか？って言うか、輻射の式が ρ を独立 変数にした式に直せるのかな？ ) |
その他のパラメタ― 星の表面温度は T*=2400 K で統一した。 輻射輸達式を解く時、まず規格化シェル内径 ρi = ri/R を指定する。 ri/r* = ρi(4πσTe4/Fs) 1/2 = 1.6 (グラファイト)、 = 4(シリケイト)とした。これは 凝結温度をグラファイトで 1700 K, シリケイト 1200 K とした ことに相当する。こうして、 (Te, Fs) の組に対し、ri/R が決 まる。（？） 最後に [dτλ(ρ)/dρ] を指定する。通常は [dτλ(ρ)/dρ] ∝ ρ-α (ρi≤ρ≤1) を仮定する。α = 2 が良く用いられる。 (τ は dτ/dρ の積分値 としてインプリシットに与えられるらしい。) |
  |
  |
|
L* = 3.25 104 Lo モデル 前章では、モデルと観測を比較する際に光度を特定する必要はないことを強 調した。しかし、様々な物理量の効果を理解するには、光度一定の星に関して 較べる方が簡単である。そこで、 L* = 3.25 104 (Mbol = -6.5) と指定して図２を描いた。図には "ダーティ"シリケイトとグラファイトの 放射スペクトルを示す。 抜かした波長帯 λ > 40 μm ではフラックスが小さく、短波長側から容易に外挿 出来るので省いた。λ < 0.45 μm ではオパシティ、アルベド等の 不定性の影響が大きいので、やはり省いた。 光学的深さ 図には τ(10μm) を示したが、他の波長での光学的深さは表１用いて 容易に計算できる。我々の目的は個々の天体スペクトルのフィットではない ことを強調しておく。 Ｒ＝シェル外側半径 図２には R = 6 1015 cm = 8.6 104 Ro = 400 au のスペクトル を破線で示す。R*224004= 3.25 104 Ro257774 から、 R* = 868 Ro = 4 au だから、R/R* = 100 (論文には 80 とある？)、 Fs = 3.25 104 3.85 1033/(6 1015)2 = (3.25*3.85/36) 107 = 3.6 106 erg s-1 cm-2 である。 (マスロスの数百年分にしかならない。) シリケイトシェルに対してはさらに、R = 3 1016 cm = 8.6 104 Ro, つまり、R/R* = 400, Fs = 1.4 105 erg s-1 cm-2 の場合と、 グラファイトについては R = 2.4 1016 cm = 7 104 Ro, つまり、R/R* = 320, Fs = 2.3 105 erg s-1 cm-2 の場合を実線で示した。 |
 図３．ダーティシリケイト（上）とグラファイト（下）の 温度分布。破線：τ=0 の場合。黒丸：n = 一様。 三角： n ∝ r-2 グレインの分布 グレイン分布はべき乗則に従うことを仮定した。図２にはいくつかのべき乗 指数についてのスペクトルが示されている。α > 0 の時には 見かけサイズは R より小さくなるだろう。R 位置での輻射の角分布は計算 していないが、幾つかのケースでは特別にレイトレースを行った。一般的には ある波長での見かけの大きさはダスト温度がウイーンのピーク波長則温度 になる、つまり Td = 3000/&lambga;(μm) の半径である。図３には α の変化に伴い Td(r) がどう変わるかを示す。 |
|
Td 分布 散乱の光学的深さが短波長で大の時には、シェル内側でその波長の光子輸送 は拡散的になる。吸収の光学的深さが波長数ミクロンの領域で大の時には全波 長で光子輸送が拡散的となる。α < 0 ではその結果内側で粒子過熱 が大きくなる。この傾向は図３に見て取れる。光学的に厚いシェルの外側部分 ではグレインの加熱には星からの直接光より、他のグレイからの拡散赤外光 の方が効く。しかし、赤外では 10, 20 μm ピーク付近を除きグレインが 透明なためグレイン温度は光学的に薄い場合より低くなる。 内側シェルが隠される まず簡単なグラファイトシェルを考える。このシェルは近赤外で厚いので、 シェル内側は直接は見えない。一般には τ(λ) = 1 の温度を見ている と考えると、波長が短くなるほど外側低温部を見ることになる。このため、 短波長側 SED は、単一温度黒体輻射よりも急な勾配となる。 |
 図４a．τ10μm = 2.0 n ∝ r-2 の時の温度分布。破線：ダーティシリケイト。 クリーンシリケイト：グラファイト＝４０：６０に混ぜた時、 実線：クリーンシリケイト。一点鎖線：グラファイト。 点線：Qabs = 0.01 (λ ≤ 5 μm) の場合 |
|
１．クリーンシリケイトはダメ クリーンシリケイトは観測スペクトルを再現しない。 ２．ダーティシリケイトなら可能 可視、近赤外で吸収率を上げたシリケイトなら再現可能。 ３．混合の扱い 数種のグレインが共存する時には、合体光学定数を使ったモデルではＳＥＤ 再現ができない。それぞれのグレインが個別の平衡温度を持つ必要がある。 |
４．吸収バンドの条件 Td < 250 = 10 μm のウイーン温度のダスト部分だけで光学的に 厚くならないと、吸収帯が生まれない。 表面での角度分布 表面輻射の角度分布の計算が望ましい。 ５．ダイナミカルモデル ダイナミカルモデルも大事 |