WIYN Open Cluster Study III. the Observed Variation of the Red Clump Luminosity and Color with Metallicity and Age

　アブストラクト　

　１．イントロダクション　

　２．観測データ　

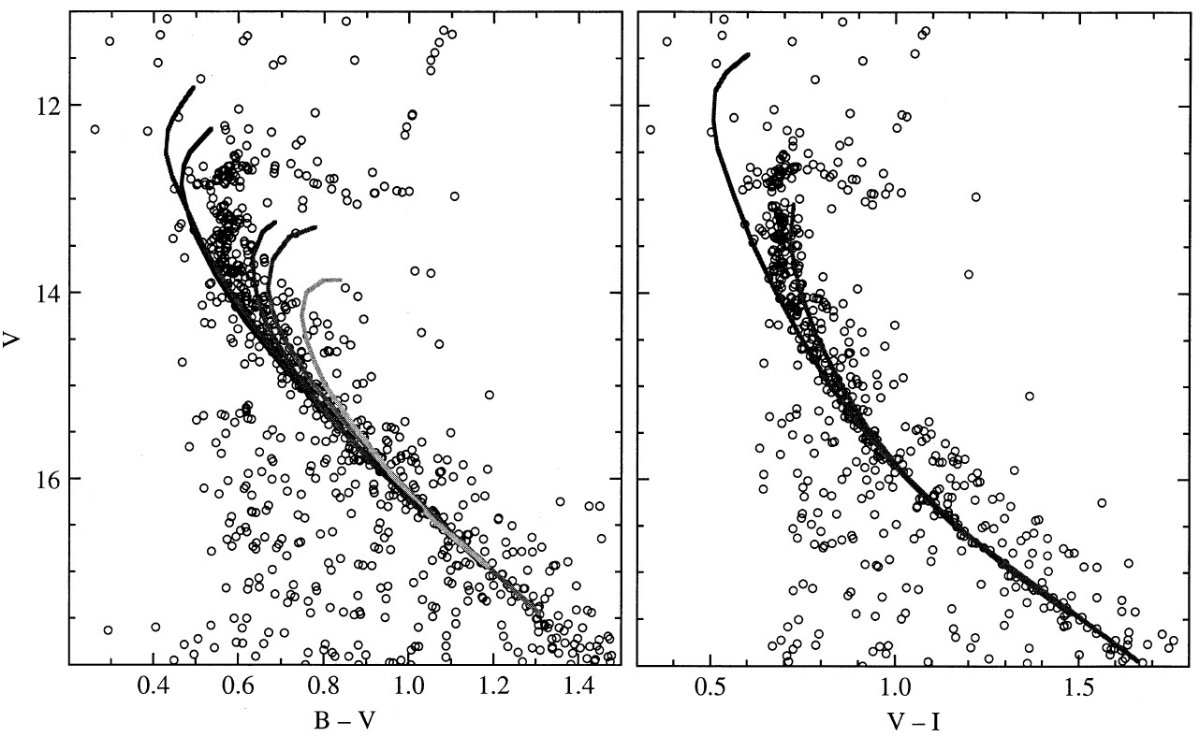
データベース　 　散開星団観測に際し、 Twarog, Ashman, Anthony-Twarog (1997) が最近整備したデータベースは貴重である。彼らは 75 散開星団の [Fe/H] と E(B-V) を公表した。メタル量は全て同一のシステムで決定されている。一方、 赤化は内部矛盾のない方法で決められている。我々はこの表から CCD VI 測光 が未進化主系列にまで達している星団を選び出した。表１にそれら 8 星団を載 せた。そこには Twarog, Ashman, Anthony-Twarog (1997) から採った [Fe/H] と E(B-V) も載せてある。NGC 6819 と NGC 7789 の E(B-V) は最近の観測値を使用した。第９列は CMD の出典である。 NGC 778 と Mel 66 以外は B-V と V-I データを含んでいる。 　距離指数　 　距離指数を出すには、存在する限り B - V CMD を使用した。なぜなら、その 方が主系列を定義しやすいからである。主系列フィットには差分法を使用した。 M 67 を基準にし、他星団の見かけカラーを M 67 と対象星団との赤化とメタル 量の差に対して補正した。Bertelli et al 1994 の等時線から、下部主系列 Mv = [5.5, 6.5], [Fe/H] = [-0.4, 0.4] で Δ(B-V) = 0.215Δ[Fe/H]. Δ(V-I) = 0.150Δ[Fe/H] である。相対補正済み主系列の等級差＝星団と M 67 との距離指数の差である。 M 67 に対しては与えられた赤化量を使い、B - V CMD の下部主系列フィット から (m-M)v = 9.79±0.10, V - I CMD の下部主系列フィット から (m-M)v = 9.73±0.10 を得た。こうして得た距離指数（表１）は Twarog, Ashman, Anthony-Twarog (1997) と良い一致を示した。NGC 188 に関しては我々の測光ゼロ点に直し、距離を 求めた。我々の距離指数ー Twarog97 距離指数 = -0.063±0.040 であった。 I バンドに関しては AI = 1.96 E(B-V), E(V-I) = 1.28 E(B-V) ( Udalski (1998b), ) を採用した。 　絶対等級の決定　 　クランプを中心とするボックス内の星の等級とカラーのメジアンを取った。 これは箱の選択にあまり影響されない。表１にはこうして決めた IRC と (V-I)o を載せた。距離指数と赤化を使うと MVRC, MIRC, (V-I)o を決めることが出来る。 　星団年齢を決める実際の手続き　 メタル量と赤化情報に基づいて、距離を下部主系列で決めた。図１には M 67 星のプロット上に他の星団にフィットした基準等時線を引いた。それから、 各星団の TO 等級を決め、そこに M 67 距離指数を適用して MVTO を得る。

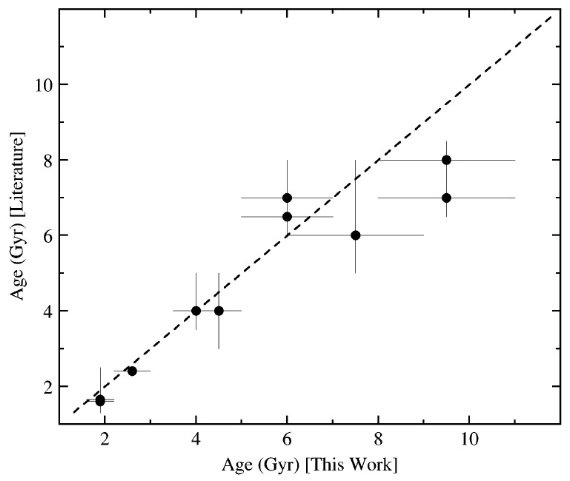図２．今回求めた等時線年齢と文献年齢の比較。破線＝等値。 比較年齢の文献省略。 第２に Montgomery, Marshall, Janes 1993, Sarajedini et al 1999 の研究 から、M 67 に t = 4.0 Gyr を与えた。次に Bertelli et al. 1994 等時線 を使って他の星団の M67 に対する相対年齢を決める。Bertelli et al. 1994 等時線は M 67 に 3.5 Gyr を与えるので、それでフィットした他の星団には 0.5 Gyr の下駄を履かせる。これ等の年齢は表１の第８列に載っている。 　年齢チェック　 　チェックのために図２には我々の決めた年齢を他の研究値と較べた。 (0.5 Gyr の下駄が必要だったのだ ろうか？ )

　３．結果と議論　

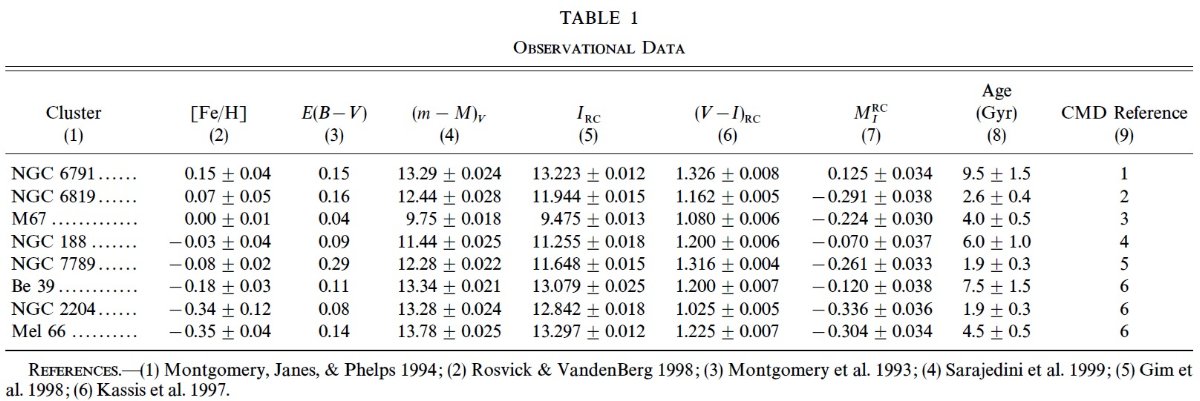
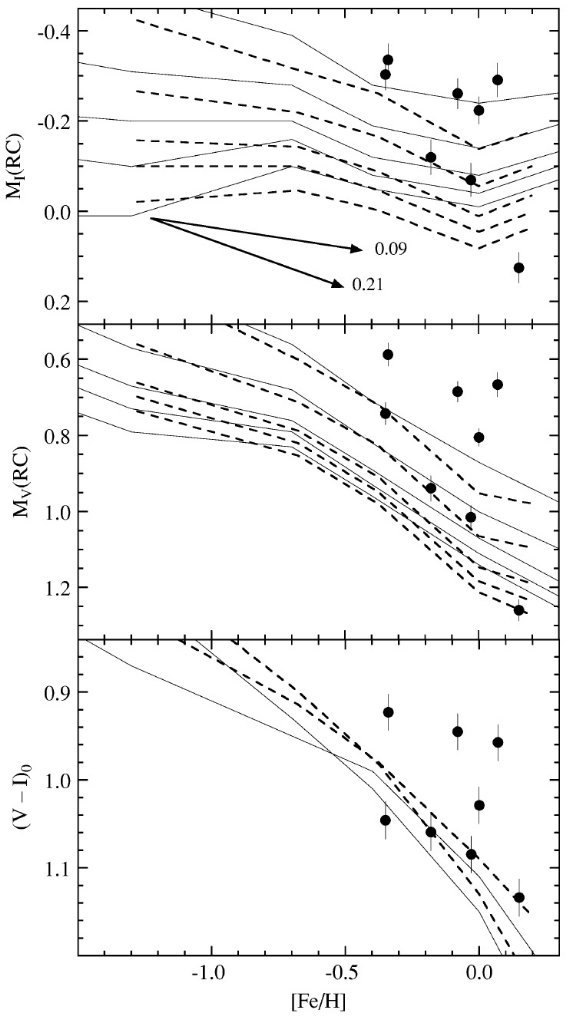図３．上＝ I 等級、中＝ V 等級、下＝ (V-I) カラーの [Fe/H] による変化。 黒丸＝銀河系散開星団。実線＝ Bertelli et al 1994 モデル。破線＝ Girardi 1999 が年齢 2.5, 5.0, 7.9, 10.0, 12.6 Gyr について求めた メタル量依存性。矢印＝ MIRC - [Fe/H] 関係を 表す二つの勾配例。 　観測データとメタル量との関係　 　前節で扱った観測データとメタル量との関係を図３に示す。 ⟨MVRC⟩ = 0.84±0.24, ⟨MIRC⟩ = -0.19±0.16 である。エラーは Keeping 1962 の少数サンプルの統計公式を用いた。興味深 いことに、もし NGC 6791 を外すと、 ⟨MIRC⟩ = -0.23±0.03 となる。 この値は Stanek, Garnavich 1998 が太陽近傍レッドクランプについ て得た値に近い。ただしこれはレッドクランプの ⟨[Fe/H]⟩ = -0.13±0.05, ⟨Age⟩ = 4.1±0.7 Gyr 集団についてであるが。 図３の実線(Bertelli et al 1994)と破線(Girardi 1999) は上から下へ t = 2.5, 5.0, 7.9, 10.0, 12.6 Gyr モデル曲線である。図３の一番下では t = 2.5 Gyr と 12.6 Gyr のみを示した。 二つのモデルは一般に良く合っている。 図３上枠中の矢印は ΔMIRC/Δ[Fe/H] = 0.09 と ΔMIRC/Δ[Fe/H] = 0.21 を 示している。 (前章で年齢を議論してたのに、突然それを 棄ててメタル依存の話に切り替えてる。)

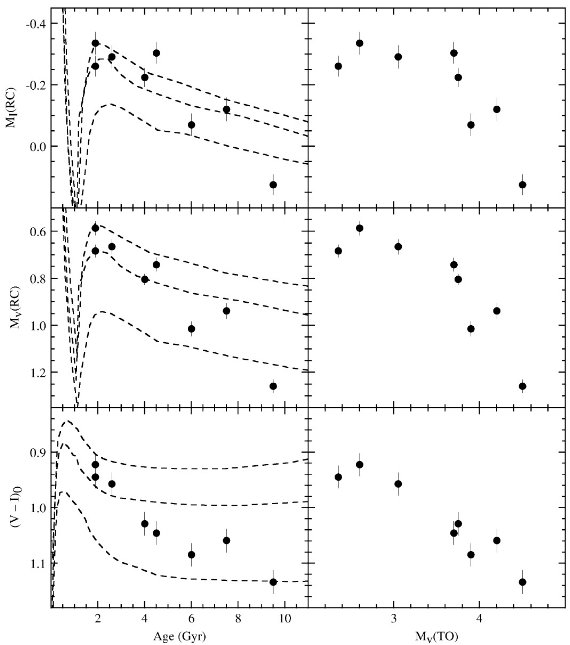図４．図３と同じだが、 年齢による変化を示す。左列の年齢は等時線フィット から決めた。右列は主系列ターンオフの位置による変化。左列破線＝ Girardi 1999 による Z 0.004, 0.008, 0.019 モデル。 理論曲線と較べると 0.21 は t < 5 Gyr に、 0.09 は t > 5 gyr に 適当である。V バンドのメタル量効果は I バンドより大きいが、年齢効果は 同じくらいである。 (年齢とメタルが混ざったデータで 片側だけを取り出した議論は変？) そのモデル予測は観測とも一致する。 　MIRC が良い標準光源か？　 　しかし、MIRC の散布度は個々の観測エラーよりも 大きい。これは MIRC が良い標準光源であるという主 張に疑問を投げかけるものである。 　年齢と　RC 等級の関係　 　そこで図４では年齢との関係を示した。図左枠は等時線フィットから導いた年齢、右枠は 主系列ターンオフ光度から決めた年齢を横軸にしている。左枠の破線は Girardi 1999 の Z = 0.004, 0.008, 0.019 モデル等級である。図３と図４から、観測 に示される傾向はモデルでも追従されることが判る。つまり、レッドクランプ星 は古い星、高メタル星ほど暗く赤いのである。 　モデルに問題？　（１）年齢　 　これ等のグラフを詳しく見ると、モデルに少し問題があることが判る。例え ば図４に見えるように、 t = 1.0 - 2.0 Gyr モデルは MIRC, MVRC の激しい上下動を 示している。t = 1 Gyr より若くなるとレッドクランプはまた明るくなる。 しかし、図３で最も若い等時線より上にある明らかに 1.0 Gyr より古い。 モデルの年齢かモデルのメタル組成が観測と合わないのではないかと言う 疑問と直面せざるを得ない。つまり、図３の曲線は [Fe/H] か MRC の方向にずらす必要があるのだろうか？ 　この疑問に答えるため、 （１）図４で求められた年齢はモデルと良く合っている ことに注意する。他の言い方をすると、主系列ターンオフへの等時線フィット で決めた年齢は図３中の星団位置から決めた年齢よりも理論モデルに良く合う。

モデルに問題？　（２）メタル量　　 　次に、 （２）図４のモデル系列を使い、MIRC, MVRC, (V-I)o と年齢を決める。この作業の結果を図５ に示す。そこでは求めたメタル量を表１の値と較べてある。実線は等値からゼロ点 のみを最少二乗でずらした関係を表す。破線は勾配も変数にして重み付き最小 二乗法でフィットした。上から下の図に移るにつれ、実際のメタル量とモデルから 評価したモデル量との相関は悪くなることが判る。散乱度は真ん中の MVRC を使った決定が一番小さい。また実線との距離も小 さい。図３の一番下の枠でも疑ったが、 (V-I)o から決める [Fe/H] は実際の 値との相関が最も悪い。 　モデルと観測とのズレ　 　こうして見ると、モデルは定性的にはレッドクランプの観測に合っている。 しかし、より詳しく見ると、モデル予測と観測の間に乖離が見つかる。具体的 には、MIRC と MVRC を 使うと年齢を過小に評価し、メタル量もやや少なく見積もる。 　観測誤差と比較対象の問題　 　勿論、問題のいくらかは観測精度に帰される。また、観測ではレッドクラン プ分布のピークを使っているのに対し、モデルの方はレッドクランプになった ばかりの位置を較べていることもズレを生み出している。

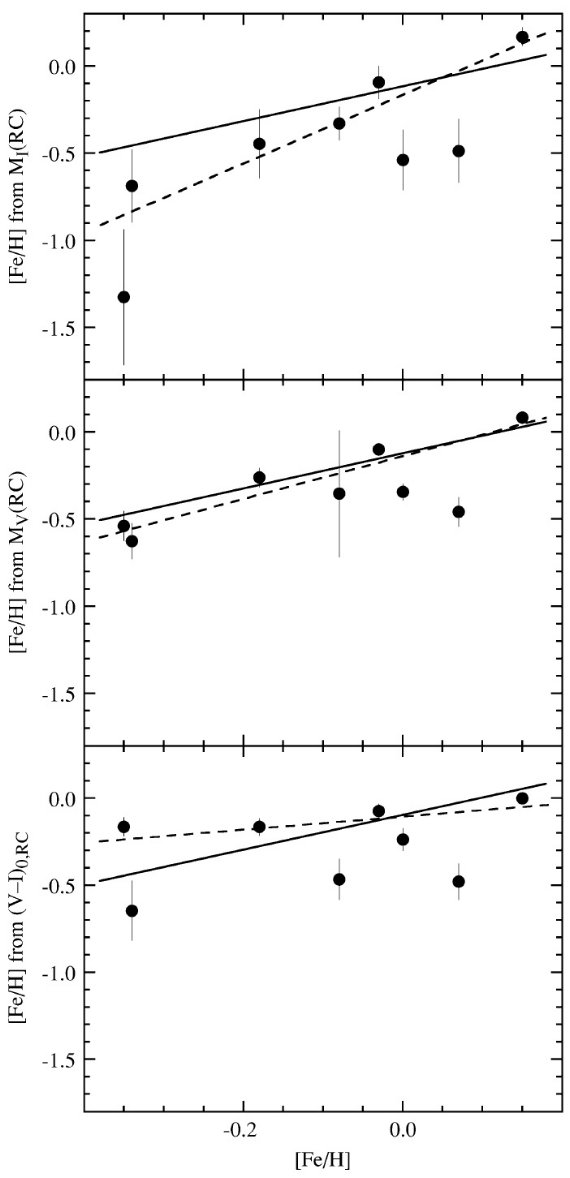図５．横軸＝表１で採用した [Fe/H] と縦軸＝Girardi 1999 モデルに今観測で 決めた星団年齢と、上＝ MIRC、中＝ MVRC、下＝(V-I)0RC を 使用して決めた [Fe/H] との比較。

　４．まとめ