OGLE The Distance Scale: Galactic Bulge-LMC-SMC

　1.イントロ　

　２．観測とデータ　

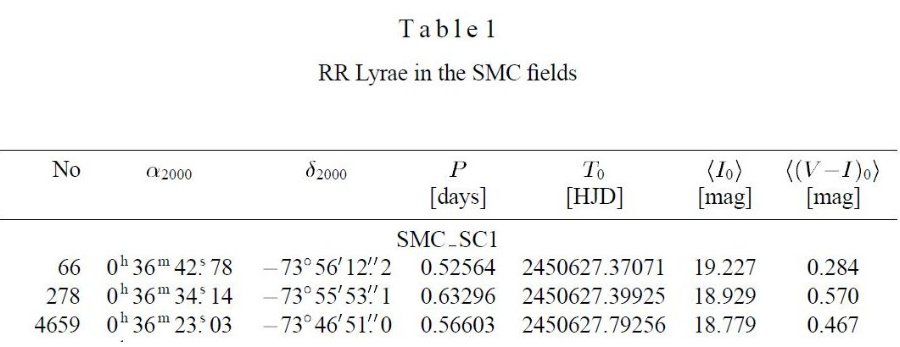
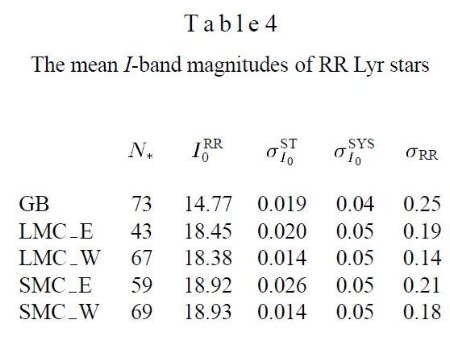
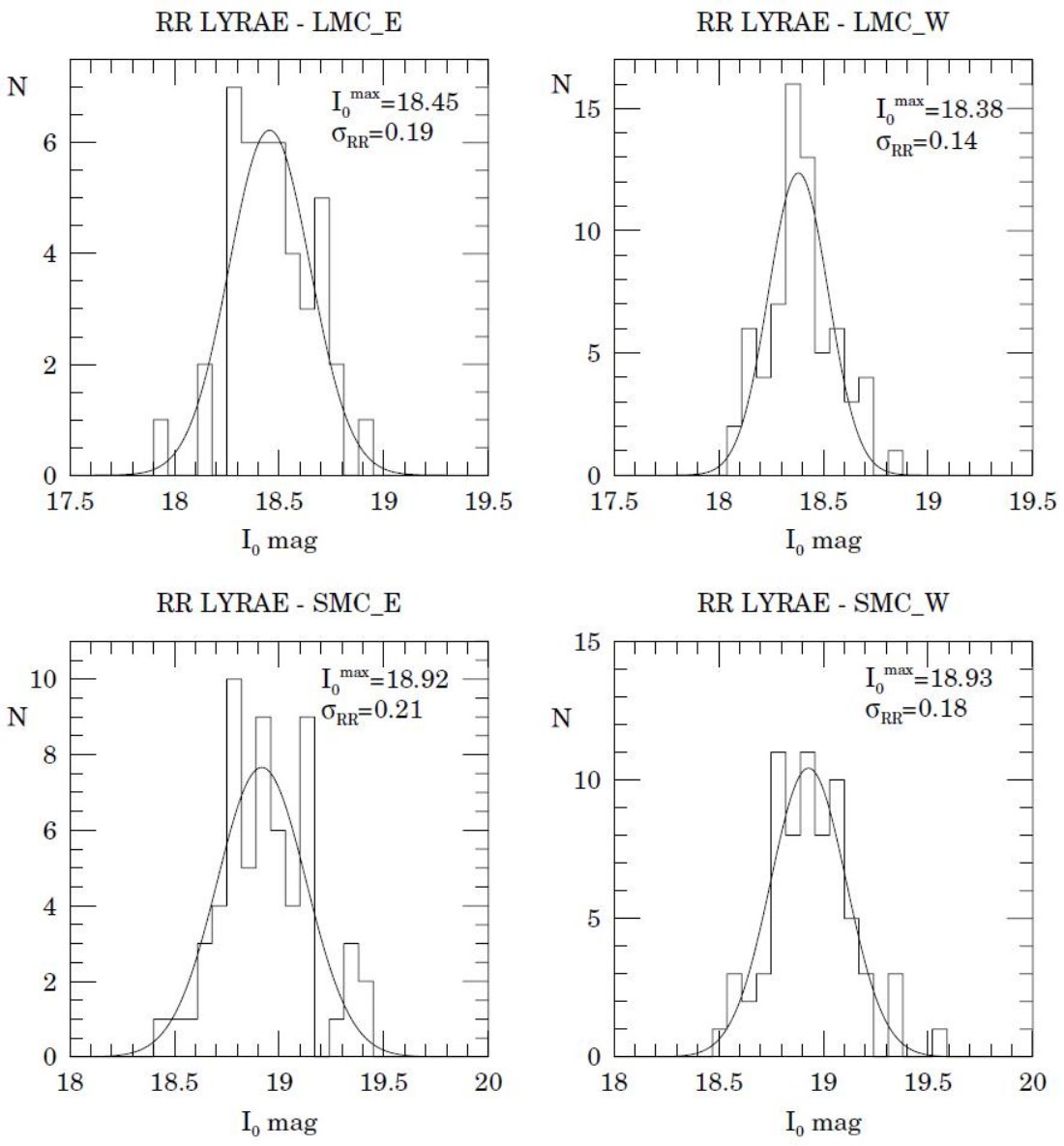
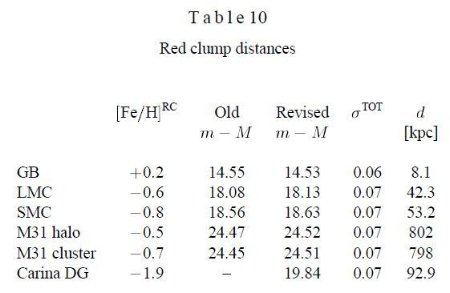
SMC の RR Lyr　 　SMC の RR Lyr はカタログとして近いうちに公表するが、今回は Udalski et al 1998 がレッドクランプをサンプルした同じ領域から選んだ。その領域は SMC_SC1, SMC_SC2, SMC_SC10, SMC_SC11 で、各領域の大きさは 14'×56' である。各 RR Lyr 毎に 100 - 115 回の I 測光が行われた。V 測光は 20- 25 回行われた。SMC フィールドからは 128 RR Lyr が選ばれた。 　RR Lyr の一つ SMC_SC11 101421 は NGC 419 の中心から 87" しか離れていない。 NGC 419 は 3 Gyr とかなり若い (Bica, Dottori, Pastoriza 1987) ので、これは 偶然の一致だろう。SMC では NGC 121 のみが RR Lyr を含んでいる（Olszewski, Suntzeff, Mateo 1996）。それにもかかわらず、星団の構成が単純でない可能性 を含め、この星には注意しておく必要がある。 LMC の RR Lyr　 　LMC の RR Lyr は予備的データベースを使い、LMC_SC14, LMC_SC15, LMC_SC19, LMC_SC20 から取った。赤化の微分変動を避けるため、 1/3 領域しか調べていないが、これはレッドクランプも同様であった。その結果、 110 星が選ばれた。 データ較正　 　OGLE 測光のゼロ点精度は SMC で 0.01 等、 LMC では　0.01 - 0.02 等である。 図１，２は RR Lyr のサンプル光度曲線である。表１，２には変光パラメターを載せた。 バルジ　 　バルジ RR Lyr は OGLE-1 データベースから選ばれた。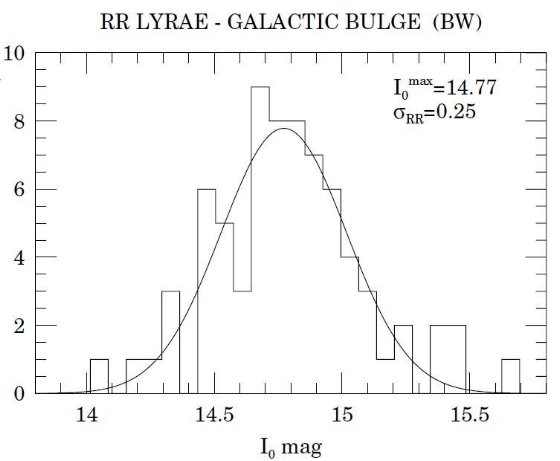場所は http://www.astrouw.edu.pl/~ftp/ogle である。Stanek 1996 が減光マップを作った BW 1-8, BWC から RRab 73 星が取られた。 混んだ領域なので I 等級ゼロ点の精度は 0.03 等である。表３には変光パラメターを 載せた。

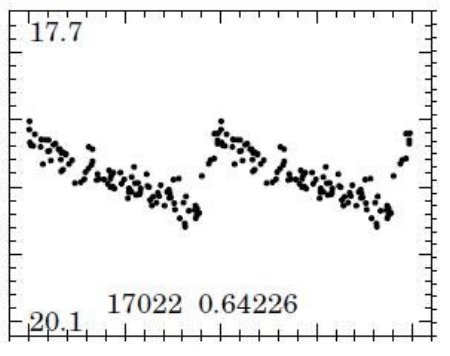
図１．SMC_SC1 RR Lyr のサンプル変光曲線。縦軸は 0.1 等目盛り。 カリーナ銀河　 　OGLE-II の副プログラムとして、カリーナ銀河の観測も始まった。これまで　20 の V, I 画像が RA2000 = 6h41m34s, Dec2000 = -5-° 58'00" を中心に 14' × 14' で撮られた。

　３．RR Lyr 距離スケール：バルジ - LMC - SMC

３．１．RR Lyr データ RR Lyr の平均等級 　 　各天体の平均等級を求めた。まず、各星のフラックス重み付きの平均等級を計算した。 変光カーブを高次多項式でんフィットし、平均を求めた。結果のチェックにフーリエ 級数での近似でも同じ計算をした。二つの結果は 0.01 等内で一致していた。 減光を評価　 　次に、減光を評価した。バルジには Stanek 1998 の減光マップを Gould, Popowski, Terndrup 1998 および、 Alcock et al 1998 の減光ゼロ点で補正したものを用いた。マゼラン雲に対しては、LMC_SC14, LMC_SC15 に 関して AI = 0.33, LMC_SC19 と LMC_SC20 に対して AI = 0.33 , SMC フィールドには全て AI = 0.16 を適用した(Udalski et al 1998) RR Lyr 星の平均等級　 　次に、各星の平均等級を 0.07 等のビンでヒストグラムにした。 マゼラン雲の場合、西と東の領域内のフィ ールドを融合して統計精度を上げた。ガウシアンフィットから、I0 RR = 平均等級, σIoST = 統計エラー, σIoSYS = 系統エラー, σRR = 分散 が得られ、表４ に提示された。図３、図４ にはヒストクラムとフィットを 示した。表４にある σRR はレッドクランプの分散とほぼ等しい。 マゼラン雲の分散は他の領域の分散（Smith et al 1992, Hazen, Nemec 1992）と 等しい。球状星団の分散 σRR ≈ 0.1 mag より大きい理由 は部分的には厚み効果であろう。表４の統計エラーがレッドクランプの場合より 大きいのはサンプル数のためであろう。しかし、減光マップが広がればサンプル の数は一桁は増加する。 平均等級の比較　 　表５には赤化補正後のカラー (V-I)o, Ｖ等級 Vo を載せた。表にはカリーナ銀河 のデータも載せた。観測数が少ないのでサンプルを Saha, Monet, Seitzer 1986 に限った。15 RR Lyr が検出され、E(V-I) = 0.08±0.02 (Mighell 1997) で赤化補正を行った。

表４．RR Lyr 星の平均等級。　　I0 RR = 平均等級, σIoST = 統計エラー, 　　　σIoSYS = 系統エラー, σRR = 分散 図３．バルジでの RR Lyr 星平均等級の分布。

３．２．距離の比　 RR Lyr の種族効果 　 　RR Lyr の種族効果は重大な問題である。V 等級がメタル量 [Fe/H] と線形関係 にあり、勾配が -.15 - 0.20 mag/dex であることは良く知られている。(Carney, Storm, Jones 1992, Skillen et al 1993) 議論の的はゼロ点なのだ。我々は次の 式を採用する。 　　　　　MVRR = (0.18±0.03)[Fe/H]RR + const この関係が銀河系内の RR Lyr 星の観測から導かれたことを注意する。 バルジ RR Lyr のメタル量　 　我々のサンプルの平均メタル量はどのくらいだろうか？　バルジでは、 Walker, Terndrup 1991 が分光サーベイを行い、バーデの窓 59 RR Lyr 星の平均として、 [Fe/H]RR = -1.0、σ = 0.16 を得た。OGLE-I RR Lyr 星変光 曲線のフーリエ解析から Morgan, Simet, Bargenquast 1998 は[Fe/H]RR = -1.14±0.24 を得た。 LMC/SMC RR Lyr のメタル量　　 　マゼラン雲 RR Lyr 星のメタル量に関しては殆ど知られていない。良質分光データ の取得は今や容易である。一般には、銀河系と同様フィールド RR Lyr 星は球状星団 　RR Lyr 星より高メタルと思われる。以前の結果では LMC フィールドで [Fe/H] = -1.3 to -1.8 (Alcock et al 1996, Hazen, Nemec 1992), SMC フィールドで、 [Fe/H] = -1.6 to -1.8 (Smith et al 1992, Butler et al 1982) である。した がって、LMC で -1.6±0.2, SMC で -1.7±0.2 とする。平均周期はバル ジで 0.549 d, LMC で 0.571 d, SMC で 0.581 d である。平均メタル量と平均周期 の間には一定の関係が知られており、この周期も採用したメタル量と合致する。 カリーナ銀河の RR Lyr メタル量は -2.2 dex （Smecker-Hane et al 1994）とした。 いずれにせよ高分散分光観測は非常に重要である。

表６．バルジに準拠したメタル量補正後の RR Lyr 平均 V 等級 絶対等級・メタル量関係　 　定めたメタル量の差を、絶対等級・メタル量関係に入れて、バルジ RR Lyr 平均 V 等級に対して、 LMC は 0.11 ±0.04 mag, SMC は 0.13 ±0.04 mag, カリーナは 0.22 ±0.05 mag 明るいとした。表６第５列の Vo RR@GB がそれで、バルジと同じメタル量の RR Lyr がその銀河にあったら 何等に見えるかを表わしている。 系統エラー　 　系統エラーの多くは減光不定性からくる。バルジの場合、減光ゼロ点の不定性が 0.06 等 それに 測光エラーをくわえて.0.07 mag とした。 相対距離　 　こうして、LMC 距離を 1 とした相対距離を以下のように得た。 　　　　　dGB : dLMC : dSMC = (0.194±0.010): 1.00 : (1.30±0.08)

３．３．相対距離の絶対較正　 絶対等級のゼロ点 　 　RR Lyr はヒッパルコスでの信頼できる視差がない。現在最もよいデータは統計視差 である。Gould, Papowski 1998 は [Fe/H]RR = -0.16dex に対して、 MVRR = 0.77±0.13 とした。同様の結果が Fernly et al 1998 からも得られた。 ＢＷの絶対等級　 　ＢＷ　のメタル量を　-1.0dex とし、前に出した勾配を使うと、ＢＷの RR Lyr では、MVRR = 0.77 + 0.6 × 0.18 = 0.88 ± 0.13 を得る。表６から赤化補正後の平均等級は Vo = 15.41 であるので、距離指標 は m - M = 15.41 - 0.88 = 14.53 となる。総エラーの大部分はGould, Papowski 1998 の較正値の不確かさによるものである。他の天体までの距離も同様の方法で決め、表７に 示した。

表７．RR Lyr で決めた天体距離。

　４．レッドクランプ距離スケール　

RR Lyr サンプルとレッドクランプサンプル 　 　 今回 RR Lyr サンプルをレッドクランプサンプルと同じ領域から選んだ。従って、 減光補正は同じ系統エラーを被っている。レッドクランプ星の数は多いのでランダム エラーはこっちの方が小さい。しかし、 RR Lyr の場合でさえも 0.03 等程度なので 系統誤差よりずっと小さい。 レッドクランプ星平均等級　 　表８には バルジ、LMC. SMC, M31 のレッドクランプ星平均等級 I0 RC を載せた。

表８．レッドクランプ星平均等級

カリーナ銀河　 　表８にはカリーナ銀河も載せた。この銀河は LMC と同様、 古い種族と中間年齢種族の双方を持つ銀河である。カリーナ銀河は低メタルなので、 異なる環境下でレッドクランプ星光度がどのくらい安定かをテストするのはよい 天体である。 　中間年齢種族のメタル量はどう決めたのか？ 　カリーナ銀河の減光は Mighell 1997 から 0.12±0.03 とし、レッド クランプ星は 0.7 < (V-I)o < 0.9, 20.5 < Io < 18.5 から 696 星 を選んだ。このカラーは他の天体で設定したレッドクランプよりかなり青い。これは 低メタルのためである。 　するとやはり低メタルは低メタルなのか？　 図６は 0.04 等区間での Io ヒストグラムとそれへの二次関数＋ガウシアン でのフィットである。 図６．カリーナ銀河レッドクランプ星の Io 等級分布図

図５．カリーナ銀河の色等級図。星印は RR Lyr の平均位置。

４．１．レッドクランプ星の Io 平均等級　 レッドクランプ星等級は一定か？ 　 　レッドクランプ星の Io 平均等級を使った距離決定法において最大の問題は、 それが年齢、メタル量に拘らず一定であるか否かという点である。一定説に肯定的 な観測上の証拠としては、カラーの広がりに対して平均等級が一定である ( Paczynski, Stanek 1998 ), 異なる種族領域が同一の距離を与える(Stanek, Garnavich 1998)が ある。Castellani, Chieffi, Straniero 1992 によるモデル計算の結果も年齢効果 が弱いことを示している。 一方、 Bertelli et al 1994 モデルはレッドク ランプ等級が年齢、メタル量にもっと強く依存することを主張している。Cole 1998 は種族効果が 0.6 等に及ぶことを示唆した。Girardi et al 1998 は LMC のレッド クランプ平均等級は太陽近傍より 0.24 等明るいという結果を得た。このような 有様なので、観測に基づいて一定かどうかを決めることは極めて重要である。 RR Lyr を基準にする。　 　RR Lyr が良い標準光源であることは広く認められている。そこで、それに対して レッドクランプの光度を決めて、天体間の差を調べてみよう。 RR Lyr とレッドクランプは種族が違う　 ここで強調したいのは RR Lyr とレッドクランプとは異なる種族に属していることである。レッドクランプ のメタル量は広い範囲に及んでいる。例えば、バルジでは -0.3 から 0.3 まで (Minitti et al 1995)、LMC では -0.8 から -0.5 まで (Olszewski, Suntzeff, Mateo 1996)、SMC では -1.0 から -0.7 まで(Olszewski, Suntzeff, Mateo 1996)、 カリーナでは -1.9 (Mighell 1997) である。バルジ内でレッドクランプと RR Lyr の 空間分布が異なる点も両者が全く異なる種族に属していることを物語る。レッド クランプ星はバーに集中(Stanek et al 1997)し、一方 RR Lyr は球状のハロー に属する (Alcock et al 1998a) 表９．レッドクランプと RR Lyr の等級差

（レッドクランプのＩ等級ー バルジメタル量 RR Lyr の V 等級）　 　表９には（レッドクランプのＩ等級ー バルジメタル量 RR Lyr の V 等級）を示す。 図７はその値をメタル量に対してプロットした。低メタルのレッドクランプ星が 明るくなるという明らかな傾向がある。観測点を直線フィットして、 (年齢効果は無視されている) 　　　　　MIRC = (0.09 ±0.03) × [Fe/H] RC + const. 　この式の勾配は RR Lyr V 等級のメタル量依存性よりずっと小さい。我々は const. には興味が無い。次節で詳しく論じるからだ。 　ははん、きっとこの値は都合が悪いんだ！　 　理論予想との比較　 　レッドクランプ I 等級のメタル依存性は以前から予想（Bertelli et al 1994） されていた。 Cole 1998 は 0.21 ±0.07 mag/dex という勾配を、 Girardi et al 1998 は LMC とヒッパルコス レッドクランプの絶対 I 等級の間に 0.24 等の開きを 予想した。我々が得た値は勾配にして 0.09, LMC と太陽近傍との差は 0.05 等である。 このように、理論的予想は観測値に対して少なくともファクター２大きい。 ただし、この観測結果は RR Lyr の光度・メタル量関係の勾配に大きく影響される。 それが Feast 1997 の言うように 0.37 mag/dex まで大きければ、上の式の勾配は 0.20 mag/dex に 上昇し、LMC 距離も大きくなる。 図７．（レッドクランプのＩ等級ー バルジメタル量 RR Lyr の V 等級）のメタル量による変化。 　　　　点線は直線フィット。

　４．２．レッドクランプ光度の絶対較正　

太陽近傍のレッドクランプを用いた等級ゼロ点の決定 　 　太陽近傍 70 pc 以内のレッドクランプを用い、それらが [Fe/H]RC = 0.0 として、 Stanek, Garnavich 1998 はその平均絶対 光度を決めた。前節で求めた傾きを用いると、 　　　　　MIRC = (0.09±0.03)[Fe/H]RC - 0.23±0.03 という関係が得られる。 　年齢依存性がメタル依存の中にいっしょくたにされている！ 　RR Lyr の銀河系バルジの基準光度への変換　 　表 10 には I 等級一定の仮定で求めた距離指標と、今求めたメタル依存性を考慮した 距離指標を並べている。古い方法と新しい方法との差は 0.05 - 0.07 等と小さい。この 差は低メタルな天体ではもっと大きくなり得る。注意しなければいけない点は、この 新しい距離は幾分かは RR Lyr に依存していることである。 RR Lyr のメタルー光度関係 は RR Lyr の光度を銀河系バルジの基準光度に戻すのに使用された。この基準光度が レッドクランプの光度ーメタル量関係を導く際に使われたのである。 　LMC の距離　 　LMC の距離の新しい値は古い値に比べ 0.04 等大きくなった。系統誤差は 0.05 等である。 この結果、 m - M = 18.13 ±0.07 となった。同様に、 SMC では m - M = 18.63 ±0.07、バルジは m - M = 14.53 ±0.06 となる。

図１０．レッドクランプの距離

　５．議論