Zeroing the Stellar Isochrone Scale: The Red Giant Clump Luminosity at Intermediate Metallicity

　アブストラクト　

　１．イントロダクション　

　２．スケールのゼロイング　

　２．太陽の等時線　

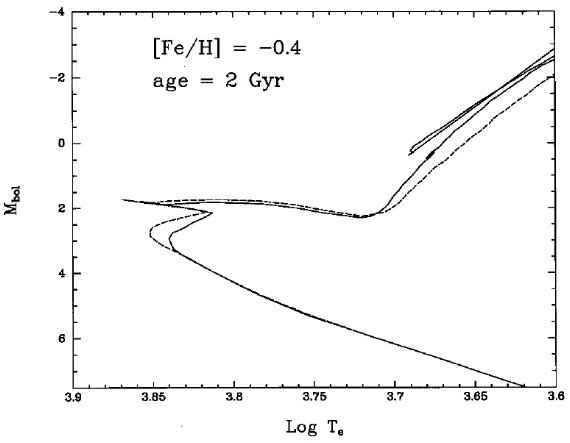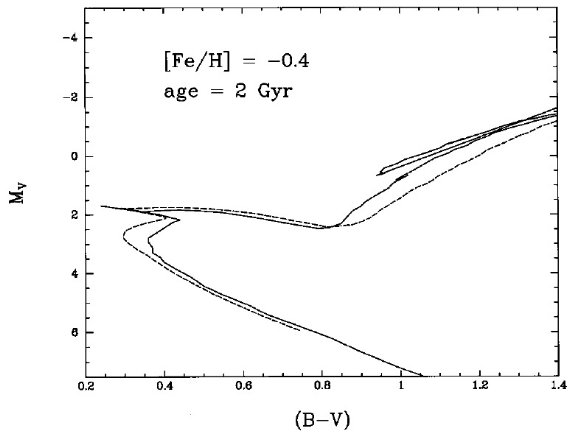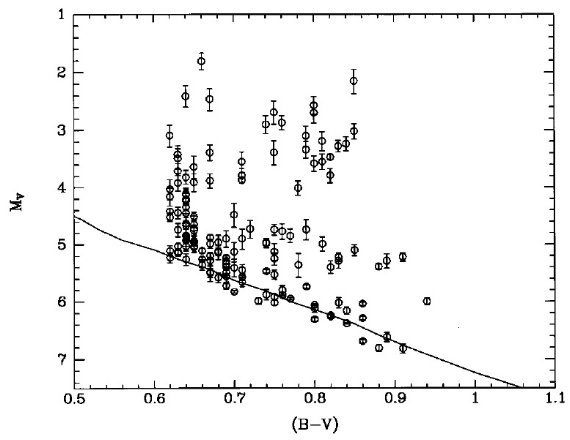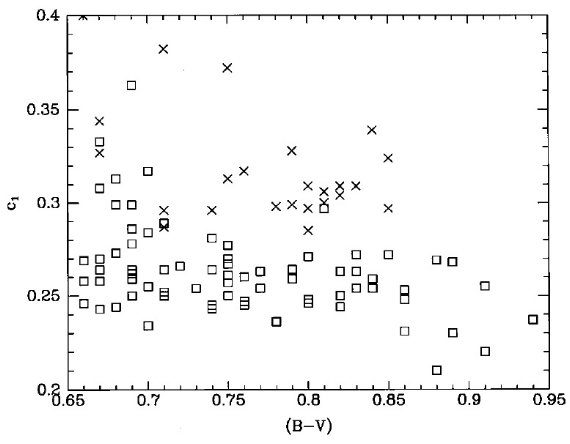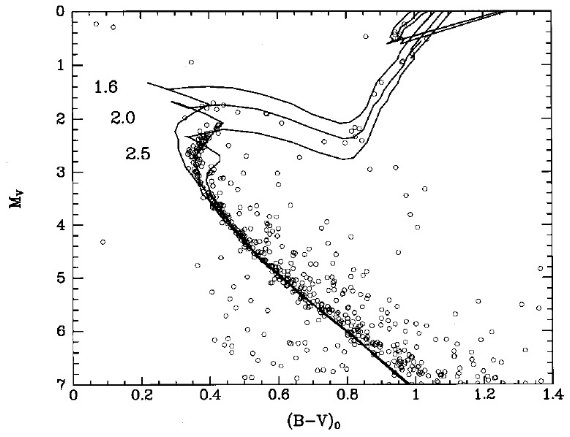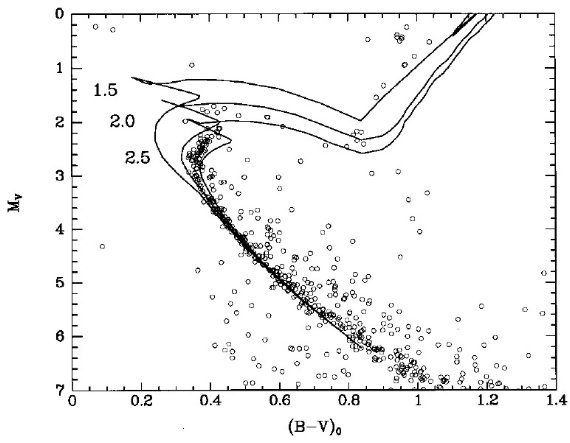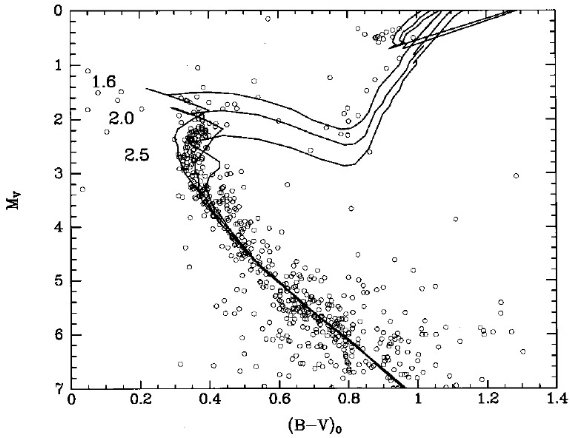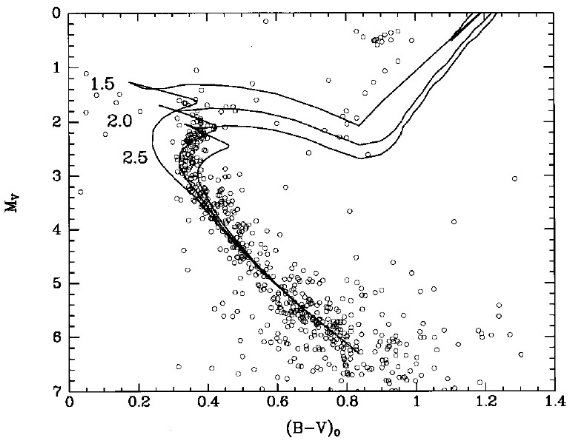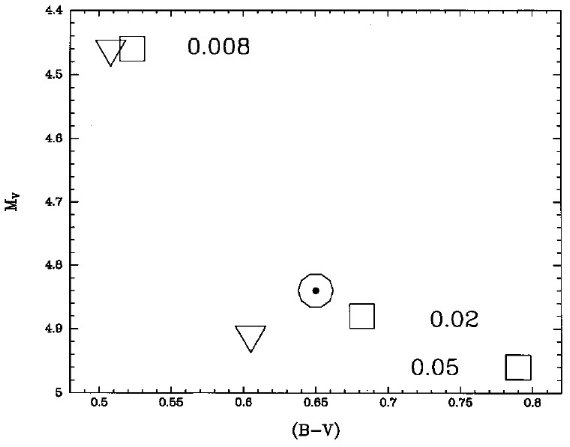
図１．(1Mo, 4.6 Gyr) 星の CMD 上の位置、メタル量は色々。 四角＝ Bertelli et al. 1994 モデル。三角＝Schaller et al 1992, 1993. 白丸＝太陽。 　太陽位置になるようオフセット　 　太陽は Mv = 4.84, B-V = 0.65 とする。Bertelli et al 1994 から Z = 0.02 （ソーラー）と 0.008 (LMC) を挟むメタル量で M = 1 Mo, t = 4.6 Gyr の モデルを (B-V, Mv) 面上に変換した。Schaller et al 1992, 1993 のモデ ルに対して同様の操作を行った。Bertelli et al. 1994 のモデルに対しては Z = 0.05 モデルに対しても同様の操作を施した。図１にその結果を示す。 Bertelli et al. 1994 のモデルで Z = 0.018 に調整すれば太陽の観測値を再 現することが図から分かる。Schaller et al 1992, 1993 は良くない。 残念なことに、どちらのモデルを使った研究でも、等時線を星団色等級図にフ ィットさせる際には Z = 0.02 モデルを太陽メタル量として扱った。図１から 分かるが、Z = 0.02 モデルを太陽組成として扱うには, Bertelli et al. 1994 モデルに対しては [ΔV, Δ(B-V)] = [-0.04, -0.032] を加え、 Schaller et al 1992, 1993 モデルに対しては [ΔV, Δ(B-V)] = [-0.07, +0.045] を加える(rezeto) 必要がある。注意しておくが、このような rezeroing はどんなモデルにも必要で当たり前のことである。

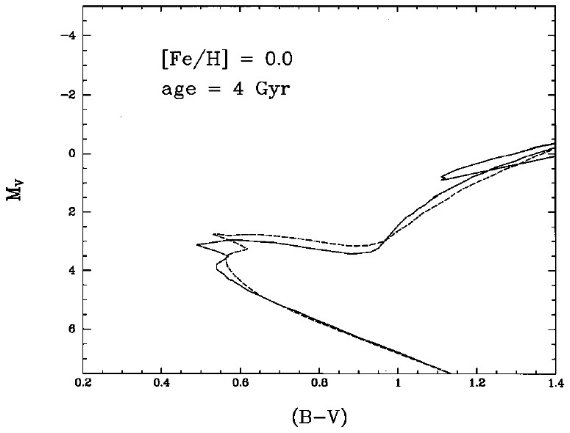
図２． t = 4 Gyr、[Fe/H] = 0.0 等時線の比較。実線＝ Bertelli et al. 1994。破線＝　Schaller et al 1992, 1993.　スケールを再ゼロ化するオフ セットを適用している。 　オフセットなしだと系統的な狂い　 　Z = 0.02 等時線に対し、以上述べたオフセットを適用すると、年齢　4 Gyr の比較は図２のようになる。未進化の主系列部は同一である。ターンオフと赤 色巨星枝のカラーは、Schaller et al 1992, 1993 モデルの方が Bertelli et al. 1994 のモデルより赤く、一方準巨星の光度は明るい。太陽組成モデルに 関してオフセットが重要なのは単にその大きさが大きいからだけでなく、 それが系統的だからである。この補正がないと、Schaller et al 1992, 1993 モデルによる主系列フィットは距離指数を 0.35 mag. 小さく出してしまう。 逆に Bertelli et al. 1994 のモデルは 0.15 大きい距離指数を与える。 年齢に関しては、Schaller et al 1992, 1993 は古すぎ、Bertelli et al. 1994 は若すぎる値を出す。

　２．２．中間メタル量の等時線　

図３．中間メタル量での 実線＝ Schaller et al 1992, 1993 モデルと 破線＝ Bertelli et al. 1994 のモデルの (log Te, Mbol) 面での 2 Gyr 等時線の オフセットなしでの比較。 　太陽組成モデルでのオフセットが与えられて、次の疑問は、非太陽組成モデル にも同じオフセット値を適用すべきか、である。 (その前に太陽組成の 4.6 Gyr 以外 の年齢に適用してよいかどうかが分からない。それとも、未進化主系列に対して のオフセット値と考えて、ＯＫにするのか？ ) 過去には他にテストする手段がなく、とりあえずイエスであった。図３に二つ のモデル等時線、t = 2 Gyr, [Fe/H] = -0.4, を重ねた。(log Te, Mv) 面上 では未進化主系列と準巨星とは殆ど同じ光度を示す。

図４．中間メタル量での 実線＝Schaller et al 1992, 1993 モデルと 破線＝ Bertelli et al. 1994 のモデルの (B-V, Mv) 面での 2 Gyr 等時線の オフセットなしでの比較。 　図４には (B-V, Mv) 面 での同じモデルの比較を示す。Schaller et al 1992, 1993 と Bertelli et al. 1994 の変換を用いると太陽組成の時と同じくらいのオフセット を期待するだろう。とまり、ある B-V に対し主系列 Mv が 0.5 mag. の差が あると。 (ここも意味不明。図２はオフセット 調整後だし、図１はターンオフ。どこから 0.5 mag という大きな値が出てくる のか？ ) しかし、明らかにそうでない。未進化主系列同士で同じ B-V での Mv の差は Schaller et al 1992, 1993 が 0.12 mag 暗い。太陽組成で決めたオフセットを 適用すると、 ある B-V に対する Mv は Schaller et al 1992, 1993 が 0.35 ] mag 明るくなる。 　どの変換が正しいのだろうか？簡単な解法は、太陽い近傍の [Fe/H] = -0.4 の小質量低温矮星の位置と等時線を一致させることである。

　２．３．ヒッパルコス星　

図５．ヒッパルコスカタログから採った [Fe/H] = [-0.5, -0.3] の星の CMD. 実線＝ Bertelli et al 1994 の [Fe/H] = -0.4 主系列。 　低メタル G 矮星　 　関心あるメタル量領域の星を分離するため、Olsen 1993 の G 型星 uvby カタログを利用した。メタル量較正は Schuster, Nissen 1989 が行い、 Olsen 1993 により測光システムの統一のため少し修正された。ヒッパルコス の σ/π < 0.1 の [Fe/H] = [-0.5, -0.3] 星をサンプルとした。 　ヒッパルコス星の CMD　 　図５にそれらの CMD を示す。かなりの星が主系列の上の方にある。Mv < 4.2 の星は準巨星である。主系列と平行する中間光度の星は多分連星である。 図６を見ると準巨星が c1 で他と区別されることが判る。

図６．図５サンプルの c1 と B-V のプロット。 バツ＝図５で準巨星領域。四角＝それ以外。 　モデル等時線のオフセットはいらない　 　太陽近傍のフィールド星と等時線を比較するために、 B-V ≥ 0.7 の赤い 星を選んだ。それより青いと主系列を離れかけている星が混ざる可能性がある からである。図５を見ると孤立主系列星と看做される星はモデル主系列から 0.3 mag 以内にある。更にエラーの逆数を重みとして調べると主系列線からの オフセットの平均は -0.005 mag 以下である。 (本当？ ) 　太陽組成の場合と鋭い対照を見せて、オフセットはない。

　３．星団： NGC 2420, NGC 2506　

　３．１．星団の基本パラメタ―　

　３．２．等時線フィット　

図７．NGC 2420 の CMD. 実線＝ Bertelli et al 1994 [Fe/H] = -0.4 モデル を [Fe/H] = -0.3 に調整。星団は E(B-V) = 0.04, (m-M) = 12.15。 図９．NGC 2420 の CMD. 実線＝ Schaller et al 1992, 1993、 [Fe/H] = -0.4 モデル を [Fe/H] = -0.3 に調整。星団は E(B-V) = 0.04, (m-M) = 12.15。 　図７＝NGC 2420 の主系列フィット　 　E(B-V) = 0.04 を適用し、メタル量が少し高いことを考慮して Mv を -0.1 mag 加えて、NGC 2420 にフィットした結果を図７に示す。(m-M) = 12.15 が 得られた。ベストフィットは t = 2.0 Gyr であった。等時線モデルよりメタ ル量が少し高いことを考えると t = 1.9 Gyr がよりもっともな値であろう。 (m-M) の決定では B-V = 0.4 - 0.6 の主系列とのフィットを最重要視した。

図８．NGC 2505 の CMD. 実線＝ Bertelli et al 1994 [Fe/H] = -0.4 モデル。 星団は E(B-V) = 0.04, (m-M) = 12.70。 図１０．NGC 2505 の CMD. 実線＝ Schaller et al 1992, 1993、 [Fe/H] = -0.4 モデル。 星団は E(B-V) = 0.04, (m-M) = 12.70。 　図８＝NGC 2506 の主系列フィット　　 　図８には NGC 2506 の主系列フィットを示す。E(B-V) = 0.04 を採用して、 (m-M) = 12.70 を得た。メタル量はモデルと同じなので、等時線の調整は 行わない。t = 1.8 Gyr でのターンオフのマッチは完全である。しかし、星団 巨星枝は少し青すぎる。 　図９，１０＝ Schaller et al 1992, 1993 フィット　 　図９，１０は Bertelli et al 1994 の代わりに Schaller et al 1992, 1993 を使ったフィットである。こちらは以下二点で少し劣る。まずターンオフが観測 にくらべ急すぎる。それから、等時線赤色巨星が赤すぎる。

　３．３．クランプ等級　

図１１．巨星の (V-I)o - (B-V)o 関係。三角＝ NGC 2204, 四角＝ Mel 66, まる＝ Be 39, ほし印＝ M 67.破線＝ NGC 2506 の CCD 測光データ 35 星から の関係式。実線＝ NGC 2506 関係を (V-I) 方向に -0.1 mag. ずらしたもの。 　二星団を合体　 　NGC 2420 と NGC 2506 の赤色巨星枝カラーの ±0.2 mag 内の星を 全て含めて合体して解析した。測光精度が高いので、第１赤色巨星枝星とクラ ンプ星の区別は容易であるが、この方法はより低精度の CMD で一般に使われる 手法である。その上、絶対等級の分布関数が V と I バンドで求まる。 ただ問題は NGC 2506 の Marconi et al 1997 では一部分しか V-I カラーが 与えられておらず、 NGC 2420 では I データが存在しないことである。 　(B-V) - (V-I) 関係　 　そこで、B-V と V-I の関係を NGC 2506 CCD 測光から求め、その関係を NGC 2506 の写真等級データと NGC 2420 の CCD データに適用することにした。 B-V > 0.6, V < 15.1 の 35 星から 　　　(V-I) = 0.91(B-V) + 0.24 を得た。この関係の周りの散布度は ±0.026 mag である。ただし、問題 がある。いくつかの年齢とメタル量で NGC 2506 を挟む散開星団の (B-V) - (V-I) 関係を図１１にプロットした。破線は上に示した関係式である。 短破線は破線を E(B-V) = 0.10 の赤化分動かしたものである。星団は赤化補正 済みである。しかし、赤化に大きなエラーがない限り、星は関係式に ほぼ沿って動くことは明らかである。参考星団星のプロットから [Fe/H] = [-0.7, 0.0] でメタル量による分離は見られない。 　NGC 2506 のカラーはおかしい　 　ところが、NGC 2506 の 関係式は他星団より同じ B-V に関して V-I が +0.1 高い。図１１では NGC 2506 関係を V-I で -0.1 mag ずらして描いた。このずれが、純粋に V-I のズレで生じたものなのか、 V-I と B-V 双方のずれの結果なのか決められ ない。　Marconi et al 1997 の CCD データのゼロ点にエラーがある可能性 が強い。便宜的に NGC 2506 の CCD データにエラーがあると仮定する。

図１２．NGC 2506 と NGC 2420 のレッドジャイアントクランプ等級ヒストグラム。 実線＝ Mv、破線＝ MI. 　平均等級　 　図１２には MV, MI のヒストグラムを示す。分布 ピークは MV = [0.25, 0.55], MI = [-0.65, -0.3] の間にある。プロファイルフィットからピークを得ることも可能だが、サンプ ル数が少ないことを考慮し、単純な平均として MV = [0.2, 0.6], MI = [-0.65, -0.2] が適当である。これらは表１にまとめた。 表にはまた、各星団毎での平均等級も載せてある。NGC 2420 のレッドジャイ アントクランプは NGC 2506 とエラー範囲で一致する Mv を有す。しかし、 NGC 2420 レッドジャイアントクランプの (B-V) は NGC 2506 より 0.04 mag. 赤い。このカラーの差は MI の差に反映され、NGC 2420 の方が MI が明るく、(V-I) が赤い。 　 MV, MI の不定性　 　もし、 NGC 2506 レッドクランプの (B-V) を 0.02 - 0.03 mag 赤くすると、 ( B 等級を暗くすることでなく、 V 等級を明るくすることで？ ) それは V-I, MI の差をも縮小することにつながる。そうすると、 二つの星団がほぼ同等であるという見解と合致することになる。 もし、 NGC 2506 星で決まる (B-V) - (V-I) 変換をそのまま両星団に適用すると、 前に述べたように、双方の MI は 0.1 mag. 明るく、 (V-I) は 0.09 mag. 赤くなる。この論文では中間値 MV = 0.47 ±0.04, MI = -0.48±0.05 を採用する。Eggen 1998, Twarog, Ashman, Anthony-Twarog (1997) では、測光精度は落ちるがより多数のサンプルを用いて、 Mv = [0.5, 0.7] の 範囲の値が出ている。どちらの研究も [Fe/H] = [-0.6, 0.2] 範囲で Mv の [Fe/H] 依存が弱いと結論している。

　４．応用と将来の研究