| DDO 測光と中間分散分光により組成が与えられた 76 散開星団を統一した メタル量表示に変換し、銀河系円盤の局所構造と進化の研究を行った。Ro = 8.5 kpc. 星団メタル量の分布は二つのはっきり区別されるゾーンで記述される。一つは RGC = 6.5 - 10 kpc でメタル分布は平均 [Fe/H] = 0.0 で散布度 = 0.1 dex。そこではあるにしても精々弱いメタル量勾配の証拠しかない。 R > 10 kpc ではメタル量散布度は 0.10 - 0.15 dex、平均 [Fe/H] = -0.3 でメタル量には R = 10 kpc で鋭い断絶があることが予想される。この断絶を 補正した後には、面に垂直な方向のメタル量勾配の証拠は認められない。 | R < 10 kpc の星団を過去 7 Gyr の円盤を代表すると、星団メタル量の 巾はフィールド星での分布の半分である。この結果を先のメタル量分布の断絶 と結びつけると、低メタルの R > 10 kpc フィールド星が内側へと拡散で 流入してきていると解釈可能である。これはまた、太陽は太陽円上で 4.6 Gyr 昔にできた普通の星ではないという解釈も含む。メタル量断絶は円盤球状星団 と所謂厚い円盤とで定義される銀河系の初期円盤の縁を反映していると考えら れる。断絶線の両側での化学進化の差によって生み出された [Fe/H] の初期の ずれは銀河進化を生き延びて現在の状態にまで至っている。そうであるなら、 組成勾配ゼロでの拡散は銀河中心距離に基づくフィールド星の分離を困難に する。 |
|
メタル量の中心距離による勾配 CCD観測により星団観測データの量と質は向上してきた。しかし、過去 15 年間あまり理解が前進していない分野がある。その一つが、1 Gyr より高齢の 星団間では [Fe/H] の範囲がかなり大きいのに、年齢・メタル量関係の証拠が 見つからないという問題である。これに、Janes 1979 による星団メタル量 の銀河中心距離に対する勾配の研究を組み合わせると、星団の性質を決めるの は年齢よりも銀河系内の位置の方が大きな役割を果たしていることは明らかで ある。その後の研究で勾配がより急になる等の修正はあったが、 Friel, Janes 1993 の結果は決定的であった。 |
二成分円盤 最近 Piatti et al 1995 は銀河面に垂直な方向にメタル量勾配があると主張 した。我々はこの問題をより詳しい解析で調べた。我々が発見したのは、従来 受け入れられてきた Rgc に対し [Fe/H] が線形の関係で変化し、また太陽近傍 では同じ年齢の星団間の組成に大きな散らばりがあるという見方では観測が 説明できないということである。そうではなく、円盤は二つのはっきり異なる 二つの種族に別れ、その境界は Rgc = 10 kpc にある。 |

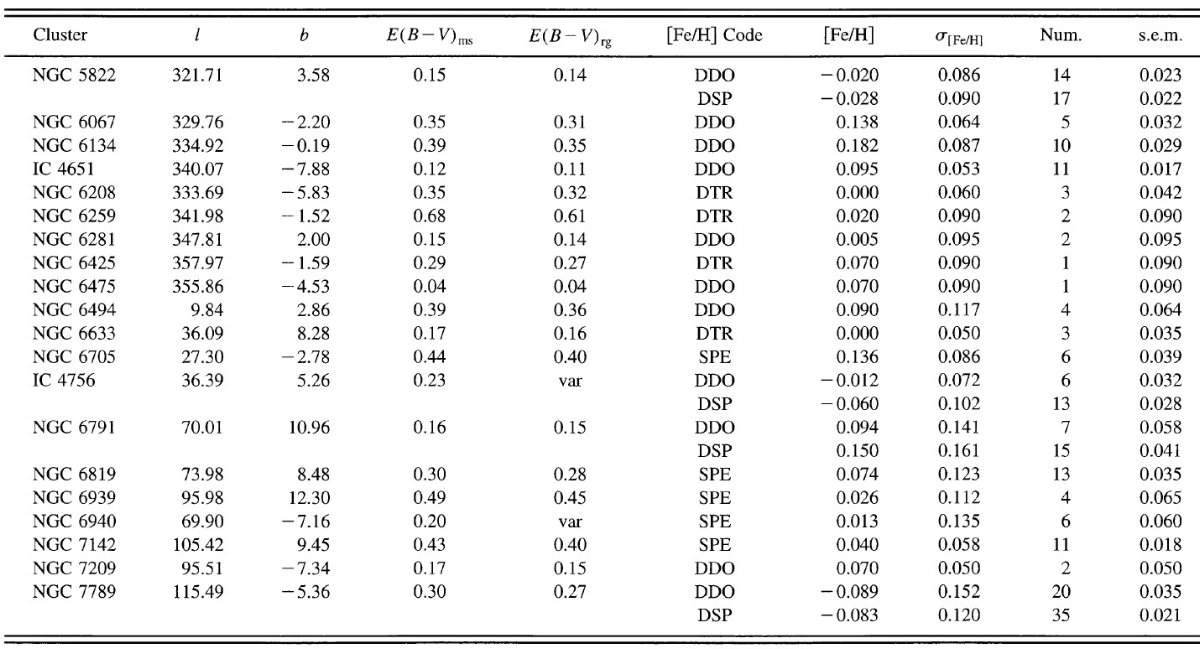
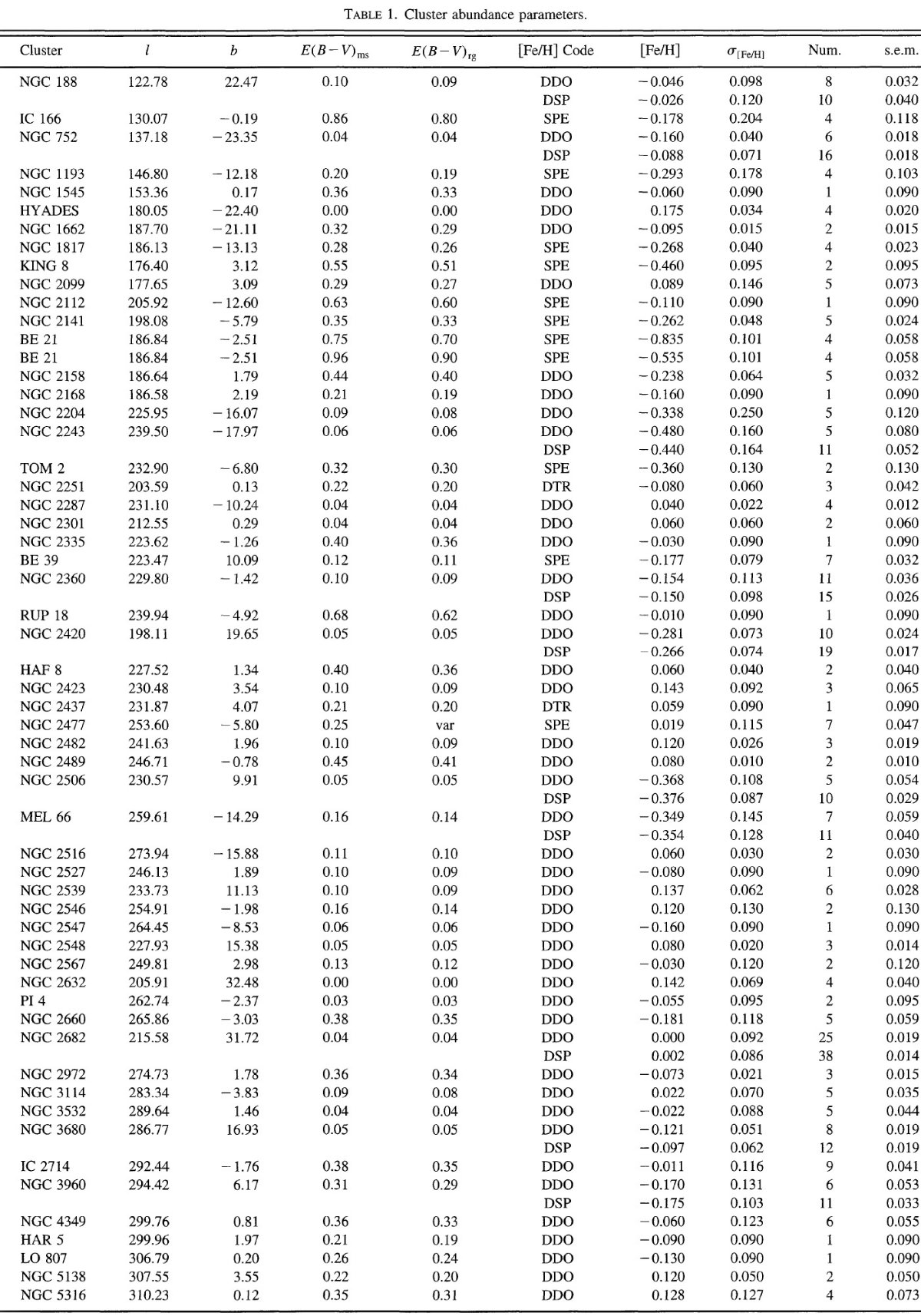
 図1a.レッドクランプ Mv とメタル量 [Fe/H] の関係。 データの整合性 メタル量が求まった星団は100個を越えるが、異なる手法の結果をただ合 わせても、星団種族内にある特徴を破壊するか、消し去るだけである。 そこで、我々は Piatti et al 1995 が使用した DDO サンプルか、 Friel, Janes 1993 の分光結果のみを使うことにした。特に Lynga 1987 は怪しい ので使用しない。 赤化の決定 赤化の決定法も論文により異なる。個々の星団につき、文献を当たり、最も 妥当に見える赤化を選んだ。Lindholm 1957, Schmidt-Kaler 1961, hartwick, McClure 1972 が示したように同じダスト層を通過しても、低温度星 の光は高温星よりも赤化量が小さい。大部分の星団では E(B-V) < 0.1 なので、この問題は無視できるが、我々は文献中の赤化が早期型星で決められ たか、晩期型星を使用したかに注意した。個々の星団に対する赤化に関しては 付録を参照。 距離決定の第1方法 BV 測光がある場合主系列フィットで距離を決める。与えられた [Fe/H] に 対する主系列モデルは VandenBerg 1985 を使用する。このモデルは太陽年齢 4.6 Gyr, 太陽組成に対し (B-V) = 0.65, Mv = 4.84 を与える。 赤化は (B-V) を E(B-V) 増加させ、V 等級を 3.1*E(B-V) 増やす。主系列の 勾配が X とすると、距離指数への影響は (X-3.1)*E(B-V) である。 未進化の主系列下部で X = 5 - 6 である。主系列フィットは 49 星団について 行った。 |
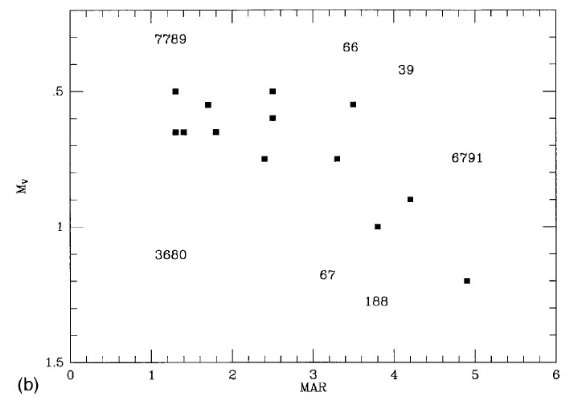 図1b.レッドクランプ Mv と年齢パラメタ― MAR の関係。図内の数字は NGC 番号。MAR は Anthony-Twaog, Twarog 1985 を見よ。 距離決定の第2方法 t > 1.0 Gyr の星団の幾つかでは主系列が暗すぎてフィットが難しい。 そのような星団にはレッドクランプ法を用いた。 主系列が良く測れる 13 星団でレッドクランプの V 等級を測った。そして それから決めたレッドクランプの Mv を図1a, b に示す。ここに、 MAR = (VRC-VBrightestTO)/(B-V)RG -(B-V)BluestTO) NGC 7789 (1 Gyr) から MEL 66 (5 Gyr) まで, レッドクランプ Mv の平均は 0.6±0.1 mag である。MEL 66 (5 Gyr) から NGC 6791 (9 Gyr) まで Mv(RC) は 0.6 mag から 1.2 mag へと低下する。NGC 6791 は最大年齢である と同時に [Fe/H] も最高なので、Mv に対する年齢効果とメタル効果を分離 することが難しい。 年齢 1 - 5 Gyr 星団には Mv = 0.6 mag とした。高メタルまたは、かつ、 高齢の星団に対しては個々に Mv = 0.7 - 1.0 mag を適用した。実際の値は 付録を見よ。この方法は 4 星団に適用された。 距離決定の第3方法 第1、第2法が適用できない場合は、文献にあるどんな方法でも構わない。 多くの場合、DDO のように巨星測光による方法、または主系列の uvbyHβ を使う方法である。第3法は 23 星団に適用された。 |
|
方針 理想的にはただ一つの方法で一人の人が全てのメタル量を決めることが望ま しい。そうはいかないので、測光法は DDO システムのみに限定する。分光は 一つのグループによる観測に限る。 2.2.1.DDO 測光DDO測光 Janes 1975 が提唱した δCN 指数は多くの研究を経て、 Piatti et al 1993 による G, K 巨星に対する ΔCN 指数となった。 Taylor 1991 は 300 以上のフィールド星に対する δCN から [Fe/H] への較正の勾配とゼロ点は温度依存があることを示 した。 Twarog, Anthony-Twarog 1996 は McWilliam 1990 の 671 フィールド巨星 スペクトルからのメタル量のみを使い DDO 測光の較正を行った。 438 巨星 から彼らは較正ゼロ点がカラーに依存するが、傾きは一定でかつ Janes 1975 より緩いことを見出した。強調したいのは Taylor 1991 と Twarog, Anthony-Twarog 1996 はヒアデス組成 [Fe/H] = 0.12 に合わせるため の小さなゼロ点シフトを施すと、非常に近い結果を与える。 2.2.2.分光DDO測光との重複Friel, Janes 1993 は星団巨星の中分散スペクトルを集めて再解析した。 内 14 星団が DDO サンプルと重なる。 |
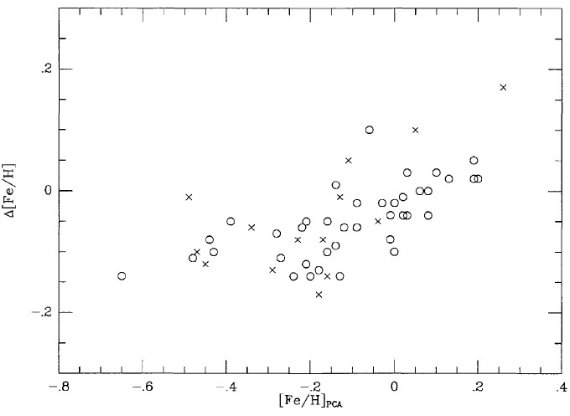 図2.DDO メタル量と白丸=Piatti et al 1995、バツ印= Friel, Janes 1993 との差と、Piatti et al 1995 との関係。Friel, Janes 1993 の [Fe/H] は Piatti et al 1995 との整合のため、 0.05 増やした。 |
| 星団のメタル量を表1に示した。第6列は手法で、 "DDO" は Twarog, Anthony-Twarog 1996 を指す。"DDT" は Piatti et al 1995 を赤化補正し、 上述の変換をしたものである。"SPE" は Friel, Janes 1993 の分光メタル量 である。DDO と SPE が被る 14 星団は "DSP" とし、平均をとった。 | 表2では星団の位置情報を載せた。第4列は距離指数の決定法である。"MSF" は主系列フィット。"RGC" はレッドクランプ法。"OTH" は何でも他の方法で 決めた距離指数。 |
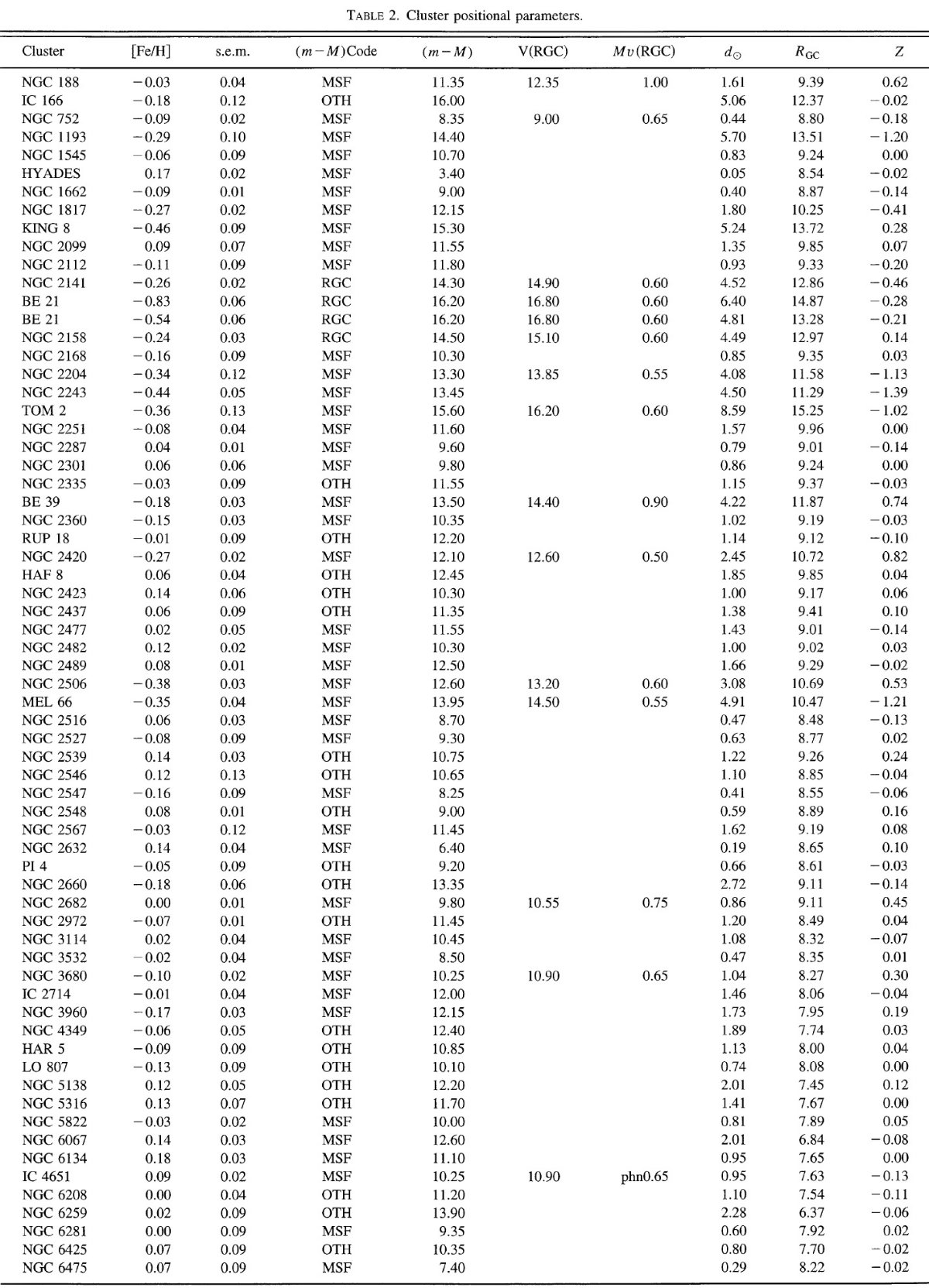
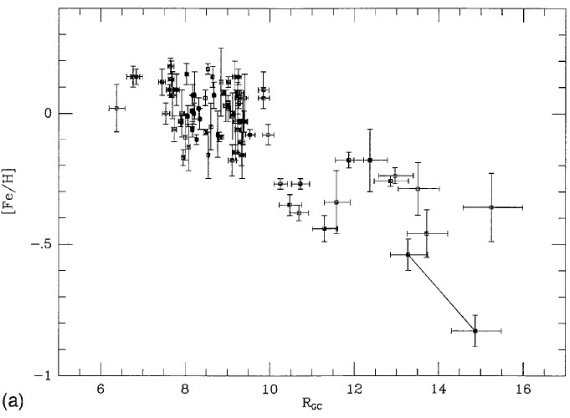 図3a.Rgc とメタル量の関係。線でつないだのは BE 21 の限界線。 エラー横棒は見かけ等級指数に全て ±0.2 mag という同じエラーを与 えた時の Rgc エラーである。 図3=表2のプロット 表2のデータをプロットしたのが図3a,b である。[Fe/H] エラーは DDOや分光法に対しては大き過ぎ、その他のデータに対しては小さすぎる であろう。 Rgc エラーはその与え方の性質から Ro 付近で小さく太陽円から 離れると大きくなる。 Rgc = 10 kpc で断絶? 図3を見ると、 Rgc = 6.5 - 15 kpc の間に [Fe/H] は大きく変化している。 しかし、それが線形変化かどうかは明らかでない。むしろ Rgc = 10 kpc で 突然の変化を示すように見える。 とりあえず、全体を線形フィット とりあえず、全体を線形フィットしてみよう。その際、BE 21 の扱いで結果 が変わる。BE 21 には低メタルと高メタルの二つの報告がある。それで、表3 では、(i) BE 21 排除、(ii) 低メタル BE 21 加入、(iii) 高メタル BE 21 加入の3通りの解を示した。 |
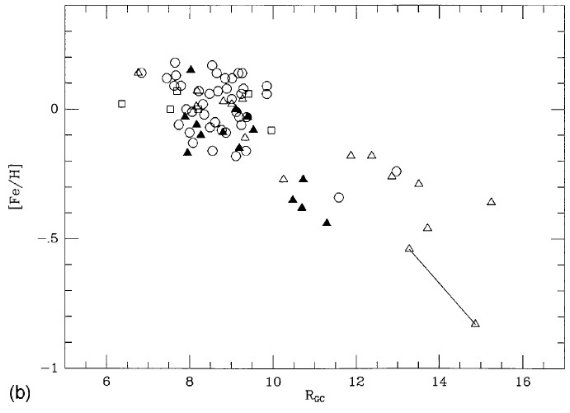 図3b.左と同じだがエラーバーをとった。白丸= DDO 測光から再解析。 白三角=分光。黒三角=DDO と分光。白四角= DDO メタルを変換。 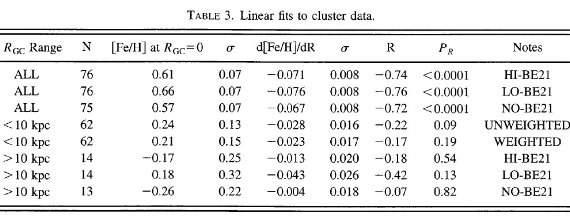 表3.星団データの線形フィット |
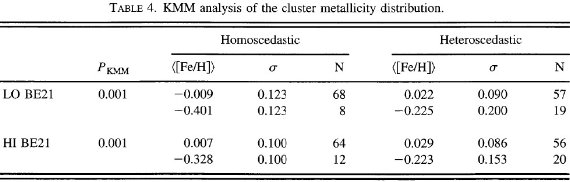 表4.星団メタル量分布の KMM 解析 Rgc = 10 kpc は本当か? もし Rgc = 10 kpc の内側 62 星団と外側 14 星団のそれぞれで直線フィットした場合はどうなるだろう?内側星団のメタル 量勾配の統計的有意性は怪しくなる。我々は夫々が平坦なメタル分布を持つ 二つのグループ説を取る。外側グループは内側より 0.3 dex 低メタルになる。 この結論が客観的かどうかを調べるために KMM 解析を行った結果を表4に示す。 断絶の原因 ではなぜこれほどはっきりした特徴が見逃されてきたのだろう?一つの答えは 、既に発見されていた、である。実際、Janes 1979, Panagia, Tosi 1981, Friel, Janes 1993, Friel 1995 などではそれらに触れられている。しかし、データの 質と量はこの論文ほどでなく、今回ほどはっきりした結論には至っていない。 サンプルバイアス 問題になりそうなのは、Friel, Janes 1993 の分光データは反中心方向星団 の大部分を占めているが、 1 Gyr より古い天体が多い。一方、 Rgc 内側は 若い星団の割合が高い。従って、仮に強い年齢・メタル量関係が存在すると、 断絶は銀河中心距離により若い星団と古い星団の寄与が異なることの反映かも 知れない。もし 1 Gyr より古い星団のみ解析したら、この問題は解消する。 |
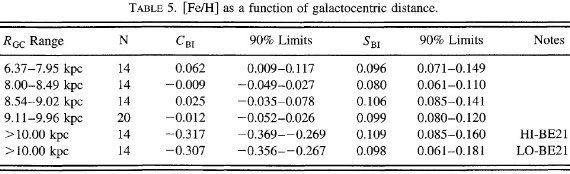 表5.銀河中心距離区分毎の平均メタル量 星のメタル分布に断絶があるか? 第4章で議論するが、 Wielen (1977) が述べているように、フィールド星は Gyr 時間では大きな距離を拡散移動する。若い星は拡散時間が不足して生誕地 点からあまり動かないので、現在のメタル量勾配の良い指標となる。ただし、 メタル量測定と、得た結果を低温度星からの結果と参照する困難さという問題 がある。Fry, Carney 1997 は Rgc = 6 - 10 kpc の 32 セファイドを分光観測 してメタル量を求めた。平均メタル量は [Fe/H] = -0.05 であり、勾配は -0.003±0.018 であった。この結果は我々が得た星団の結果と整合する。 Smart, Rolleston 1997 は星団とフィールドの 21 B 型星スペクトルを解析した。 彼らは [Fe/H] の代わりに [O/H] を求めた。O と Fe とは元素合成過程が異な るので、メタル量勾配が異なる可能性がある。Rgc = 6 - 10 kpc の 11 星は 勾配を示さない。全体の勾配は -0.06±0.09 であるが、10 kpc を越え る 10 星の効果が効いている。この結果は Luck 1982 が 50 個の晩期型超巨星 から得た Rgc = 7.7 - 10 kpc で d[Fe/H]/dR = -0.13±0.03 dex/kpc という急な勾配と明らかに矛盾する。 星雲ではどうか? 星雲の元素組成解析には多数の研究があるが、 [Fe/H] は求められていない。 それ以外に、結果がたがいに矛盾すること、距離のエラーが大きいこと等から 明確な結論を得ることが難しい。 |
Piatti et al 1995 は星団メタル量には銀河面高度による勾配が存在すると
主張した。これは従来の星団研究結果と反するが、恒星に対する結果には一致
する。図4には [Fe/H] と |Z| の関係を表3からプロットした。図5に
使用した星団の Rgc と |Z| をプロットした。Rgc < 10 kpc の星団は殆ど
|Z| < 200 pc で若い。一方、Rgc > 10 kpc の星団は古く、銀河面から
離れている。そこで、Rgc > 10 kpc の星団に [Fe/H] 段差 0.3 dex を補正
する下駄を履かせると、[Fe/H] の |Z| 異存性は消えた。
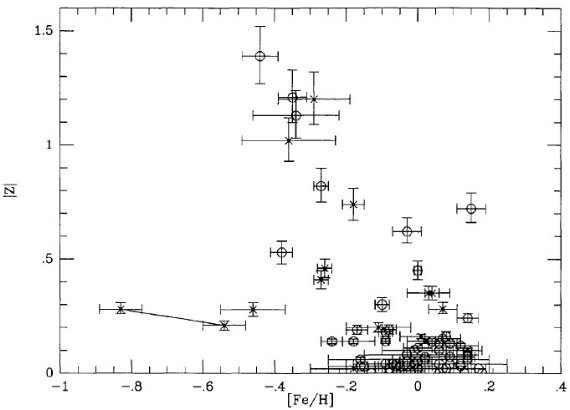 図4.銀河面からの垂直高度とメタル量の関係。データは 白丸= Piatti et al 1995. バツ= Friel, Janes 1993. |
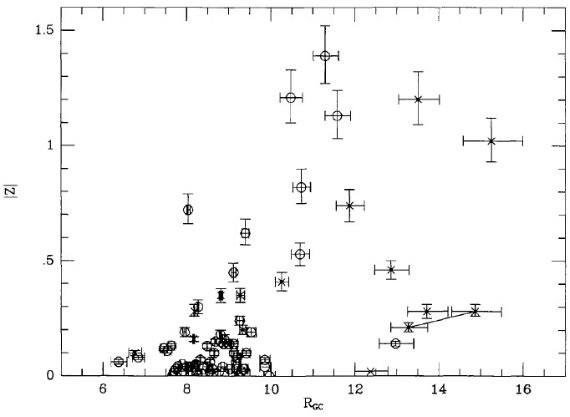 図5.銀河面からの垂直高度と銀河中心距離の関係。データは 白丸= Piatti et al 1995. バツ= Friel, Janes 1993. 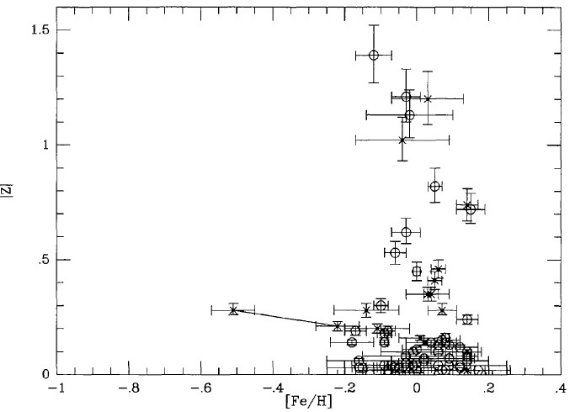 図6.銀河面からの垂直高度とメタル量の関係だが、 Rgc > 10 kpc の星団 には |Z| = 0 での段差を考慮して 0.32 dex の下駄を履かせた。データは 白丸= Piatti et al 1995. バツ= Friel, Janes 1993. |
|
星団と若い星はソーラーメタル量 Rgc < 10 kpc の 62 星団は [Fe/H] = 0.010±0.096 である。 この散布度は過去の研究より小さい。しかし注意したいのはこのサンプル が内側星団に限定されていることである。Nissen 1988 は 近傍 13 星団、年齢 0 - 2 Gyr 内の F 矮星に対して uvbyHβ 測光を行 い、[Fe/H] = 0.05±0.08 を得た。彼のサンプル中9個は我々と共通で あるが、[Fe/H] の差は 0.00±0.10 であった。 Boesgaad 1989 は 1 Gyr より若い、近傍 6 星団中の F 矮星の高分解能分 光からメタル量を決定した。彼は [Fe/H] = +0.015±0.087 を得た。 過去 5 Gyr, 太陽近傍の星団メタル量がソーラーから変化した証拠はない。 星の方では、前に述べたように、Rgc < 10 kpc のセファイドや B-型星の メタル量はソーラー±0.1 dex である。つまり、太陽近傍では若い星団 と若い星のメタル量は ±0.1 dex の誤差でソーラーなのである。さらに 星団サンプルが意味するのは、 Rgc = Ro ではこの平均メタル量が太陽が生ま れた 4.6 Gyr でも同じ値であったということである。 星雲メタル量の矛盾 しかし、太陽近傍の星雲メタル量は平均して -0.3 dex であり、太陽がその 誕生時期と場所に対して異常なメタル超過星であるという議論の根拠となって いる。われわれはその原因を星雲の解析方法にあると考えるが、この問題に対 してはこれ以上立ち入らない。 古い星種族の矛盾 若い星と星団に関する以上の一致した描像は、もし古い星まで含めると崩れ る。図7には、実線=星団、破線=厚い+薄い円盤、一点鎖線=厚い円盤の星 のメタル分布を示す。星データは Wyse, Gilmore 1995 である。星のメタル量 分布には星団に見られない [Fe/H] < -0.2 の星が存在する。星団と合致す るのは若い円盤種族の星のみである。 古い円盤星の影響? 星団サンプルは主に t < 1 Gyr でそれより高齢になると急速に数を減じ、 9 Gyr より古い星団は一つもない。フィールド星は円盤の全歴史からの星を 含んでいる。従って、もし [Fe/H] < -0.2 のフィールド星が古い円盤、 つまり t = 8 - 13 Gyr に所属するなら、星団とフィールド星のメタル分布に は差が生じるだろう。この解釈は星間ガスメタル量が t = 13 - 8 Gyr で大幅 に増加し、その後 8 Gyr は緩やかな増加に転じたという描像と合致する。また、 Twarog 1980b, Meusnger et al 1991 のフィールド星解析結果とも合う。た だし Carlberg et al 1985 はデータ選択と解析に問題があり、特に古い円盤 に関し信頼度が低い。 恒星の AMR 対照的に、Edvardsson et al 1993 と Jonch-Sorensen 1995 が見出した AMR はそれ以前の関係と大体合うが、 2 Gyr より昔で -0.2 dex 低く平行する。 実際、Edvardsson et al 1993 によると太陽誕生時の平均 [Fe/H] = [-0.2, -0.15] である。 |
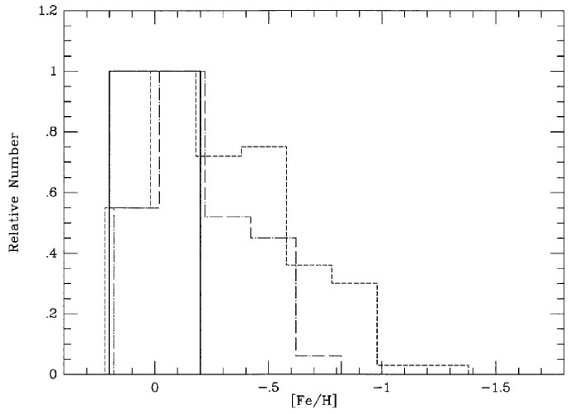 図7.メタル量分布。破線=薄い+厚い円盤。一点鎖線=薄い円盤(Wyse, Gilmore 1995)。実線=内側星団。初めの二つは見易さのため 0.02 横にずらした。 Jonch-Sorensen 1995 は殆どが Rgc < 10 kpc の 星で占められるサンプルの太陽誕生時における平均メタル量は [Fe/H] = -0.35 であった。もっと重要なことは、t = 4 Gyr またはもっと古い星ではどちらの 研究でも [Fe/H] の巾が 0.6 - 0.8 の広さを持つことである。これに対し、 Twarog 1980b は t = 4.6 Gyr で [Fe/H] = -0.05, それより若い星の散布度 は 0.1 dex であった。もし、Edvardsson et al 1993 と Jonch-Sorensen 1995 の恒星サンプルが太陽近傍、過去 10 Gyr の星間物質を代表するなら、年齢分 布の差から星団との矛盾を解消することはできない。[Fe/H] < -0.2 の星団 は年齢 2 Gyr 以上のサンプルの典型であるべきで、 1 Gyr より古い星団の メタル量はソーラーより大分低くなる。 F-型星サンプルの問題 ( F-型星をメタル量サンプル に用いる際にバイアスがかかる話らしいがよく判らなかった ) G-型星サンプル Wyse, Gilmore 1993 は G-型星を用いることで、F-型星の問題を回避した。 |
|
Rgc < 10 kpc からの低メタル星拡散 基本的な矛盾は、太陽近傍に現存する星団のメタル量分布がフィールド星に 見出される低メタル部を欠いていることである。 Edvardsson et al 1993 と Jonch-Sorensen 1995 の研究は低メタルの薄い円盤 の年齢が 2 - 4 Gyr という若さであることを意味している。では、これらの 星が太陽近傍で生まれたものでないなら、どこから来たのだろう?答えは星団 サンプルを見ると分かる。Rgc < 10 kpc には低メタルフィールド星と重なる 星団は一つもないが、その先にはそれらの星と同じ [Fe/H] と年齢を持つ星団 が多数存在する。星団はその質量が大きいため、軌道を乱される率が小さいが、 星は星同士、分子雲との遭遇の結果、数 Gyr の間に軌道が変化する。その結果、 太陽近傍には Rgc < 10 kpc で生まれた低メタル星が多数混入してきている。 星団の軌道 Carraro, Chiosi 1994, Piatti et al 1995 は星団の運動を調べた。彼らは 太陽近くの星団の Rgc は 3 kpc 程度の変動を持つと結論した。もしそれが正 しければ、我々が観測したような鋭いメタル量断絶は維持し得ない。我々は 星団軌道の決定精度が低いことが、この矛盾の原因と考える。例えば、 Piatti et al 1995 の 19 星団から NGC 7789 (e = 0.6) を除いても、平均 e = 0.19 であり、これは年齢群に分けても変わらない。しかし、新しい星団の e は 0.2 よりも 0.0 付近にあるべきで、 Piatti et al 1995 の信頼度を 疑わせるに十分である。 太陽誕生位置の拡散説による推定 Edvardsson et al 1993 以降、与えられた年齢の星の間でのメタル量の散ら ばりに関し多くの研究がなされた。van den Hoek, de Jong 1997 によいまとめ がある。多くの提案の中で Wielen et al 1996 の説が注目される。彼らは太陽 が何処で生まれたかを研究した。彼らは 4.6 Gyr の間に太陽は誕生箇所から 拡散したと考えた。そして以下の仮定を置く: (a) ある (t,Rgc) での [Fe/H]ISM の散らばりは年齢数 Gyr の星 の間で観測される [Fe/H] の散らばりよりずっと小さい。 (b) 円盤にはかなりの [Fe/H]ISM 勾配が存在する。 もし AMR が既知ならば、ある星の [Fe/H] をその年齢での平均 [Fe/H] と比較 し、それとの差分だけ Rgc を動かして合わせれば、その星が生まれた場所が 特定できる。こうして、Wielen et al 1996 は太陽が生まれたのは Rgc = 6.6 ±0.9 kpc とした。もっと重要なことは、Edvardsson et al 1993 が 見出した太陽近傍星の [Fe/H] の巾は拡散の結果であるとしたことである。 |
反対意見 我々の提案は基本的に Wielen et al 1996 と同じである。Edvardsson et al 1993 は Grenon 1987 に従い、拡散効果が [Fe/H] の広がりを説明するには 不十分であるとしたが、我々は Wielen 1977, Wielen et al 1996 の強い拡散 節に賛成する。van der Hoek, de Jong 1997 による拡散効果の抑制 は運動学的な点、それが O, Fe の動径方向勾配の存在に依存している点で疑問 である。 拡散説による説明 では、Wielen 1977 の拡散タイムスケールが正しいとして、矛盾はどう説明 されるだろうか? (1) 過去 8 Gyr の間, Rgc = 6 - 10 kpc の [Fe/H}ISM = 0.0 ±0.10 dex であった。時間と共に [Fe/H] の緩やかな変化はあったかも しれないが、何れの時も平均値の周りのその散らばりは ±0.09 dex か それより小さかった。簡単に言えば、Rgc = 6 - 10 kpc で生まれた星は [Fe/H] = [-0.2, 0.2] の範囲に収まる。この区間では様々なメタルの勾配は緩いかない かである。こうして、太陽は 4.6 Gyr 以前の太陽近傍地点の典型例ではない。 [m/H] 勾配が無いので、太陽は Rgc = 6 - 10 kpc のどこで生まれた可能性も ある。 (2) Rgc = 10 - 15 kpc でもほぼ同じ記述が適用される。[Fe/H] = -0.35 ±0.25 で平均値が低く、散布度が大きい点が異なる。Rgc = 6 - 10 kpc で生まれた星が拡散で Rgc = 8.5 kpc に来ることはある。しかしそれはメタル 量分布には何の影響も及ぼさない。しかし、Rgc = 10 kpc より遠方の星が拡散 で、 2 - 3 Gyr かけて (Wielen 1977) 太陽近傍に来ると、メタル量分布に 影響する。その結果、t < 2 - 3 Gyr の星のメタル量の巾は小さいが、 それより高齢になると突然巾幅が広がり、8 Gyr までほぼ一定を保つ。 この現象は Twarog 1980b, Meusinger et al 1991, Edvardsson et al 1993, Jonch-Sorensen 1995 で確認されている。t ≥ 8 Gyr の傾向の予言は難しい。 もし Rgc < 10 kpc で AMR が 9 - 12 Gyr のどこかで急落すると、 現在観測されるメタル量分散に多くの不確定パラメタ―、例えば内側星と 外側星の混合比、同じ時期の外側 AMR, 古い星の年齢決定の不定性、が 推定に入り込む。 |
|
散開星団データを集め、標準化して、解析した。その結果、
(a) 階段状の星団メタル分布 円盤星団のメタル量分布は、線形変化よりは階段型の方が良く合う。Rgc < 10 kpc では緩い勾配があるが、それはサンプルの年齢分布の効果かも知れない。 Rgc > 10 kpc ではサンプル数が小さくて内側のような勾配があるかどうか 分からない。10 kpc における断絶は平均 [Fe/H] に -0.35 dex の差を示す。 (b) 銀河面に垂直方向のメタル量勾配 銀河面に垂直方向のメタル量勾配は認められない。 (c) 星団メタル量の分散 内側星団メタル量の緩やかなメタル量勾配を補正した後、[Fe/H] の太陽 近傍でのメタル量散布度は ±0.09, 平均値は ソーラー である。 1 Gyr より古い星団の数は小さいが、[Fe/H] の平均、散布度が年齢で大きく 変化した証拠はない。 (d) 古い時代は? Rgc < 10 kpc の星団メタル量分布は太陽近傍フィールド星のそれと異なる。 同年齢フィールド星間の大きなメタル量分散を説明するために Wielen et al 1996 が提案した、(大きなメタル量勾配+拡散)説はメタル量勾配が存在しな かったために受け入れがたいが、拡散自体は有効なアイデアである。 t > 3 Gyr の星の間で見られる大きなメタル量分布の巾は、 Rgc > 10 kpc の低メタル星が拡散で混入してきた結果である。 |
なぜ断絶がある? 断絶はどう発生したのか、またそれが 10 - 12 Gyr の間どうい維持されて きたのか?データの不定性、不十分さを考慮すると定量的な説明を今すること は無理である。以下に定性的なシナリオを述べる。 内側と外側の星団の基本的な差は平均メタル量に存在する 0.3 - 0.4 dex の差である。前に述べているが、どちら側でも過去 8 Gyr の間に星団の平均 メタル量が変動した証拠はない。ただし、その間に 0.1 dex 程度の増加があ ったことは否定できない。 イールドの差? どんな化学進化モデルでも時間が経つとガスの平均メタル量はある一定値に 接近していく。おもに [Fe/H] の対数性が原因であるが。この値は星のイール ドのある割合である。イールドは星の初期質量関数、質量毎のイールド、ガス 流出などに依存する。こういう訳で、何らかの理由で、外側円盤の有効イール ドが内側円盤より低かったという説明は可能である。 |
|
我々の説明 我々は別の解釈をする。Rgc = 10 kpc の境界は新たに形成され、現在厚い 円盤と呼ばれている構造の形成時の境界の反映である。化学的、運動学的に 厚い円盤は円盤球状星団、例えば 47 Tuc や M 71、と関連が深く、少なく とも太陽円まで広がっている。散開星団の豊富なサンプルのお陰で、この境界 が 10 kpc に定められたわけである。Edvardsson et al 13 のデータを用いて Wyse, Gilmore 1996 は厚い円盤が 12 Gyr 昔、Rgc = 10 kpc 付近のメタル量 が [Fe/H] = -1.0 だった頃、に発生したと主張した。厚い円盤のメタル量が [Fe/H] = -1.0 から -0.6 まで上昇する間、ハローの平均メタル量は変わらな かった。 t = 10 - 8 Gyr の間に、内側円盤のメタル量は [m/H] = -0.6 から -0.1 まで急速に上昇し、内側円盤は厚い円盤から現在の標準的薄い円盤へと 進化した。この過程がどのくらい急速であったか不明であるが、とにかく 8 Gyr 昔には薄い円盤の平均 [m/H] はソーラーに近くなった。同じくらいのタイム スケールで外側円盤が形作られ、同じような化学進化が進行した。しかし、外 側円盤ではメタル量が当初の [m/H] = -1.0 のまま留まる。それは内側円盤で 化学進化を推進した厚い円盤期を欠いたからである。このために、長い間に 現在の内側と外側円盤の [m/H] の差が生まれた。それは厚い円盤の典型値 [m/H] = [-0.7, -0.6] とハロー遷移の [m/H] = -1.0 のあいだのズレを 反映する。 (最後の文章はよく判らない。 全体の描像も。厚い円盤の境界が 10 koc ということは、その内側で厚い円盤 から薄い円盤が発生し、その外側は別物?その別物をハロー遷移と呼んでいる? ) 拡散の影響 もし他に何も起こらなければ、太陽付近のメタル分布は3つの種族= 厚い円盤 [m/H] = [-1.0, -0.5]+薄い円盤 [m/H] = [-0.3, +0.2]+ 遷移種族(前二者をつなぐ)を反映したものになるだろう。遷移種族の大きさは その進化にどのくらいの時間が掛かりその間にどのくらいの星形成があったか による。そのどちらも不明である。 このような比較的古典的な円盤形成描像は外側円盤からの拡散過程の導入で 変化する。外側の平均 [m/H] は長い間一定であったので、拡散して来る星 のメタル量は [m/H] = [-0.6, -0.1] という遷移種族と丁度同じ範囲にある。 この拡散星が遷移種族と混ざり合って Wyse, Gilmore 1996 が言う低メタル薄い 円盤種族を形成した。 断絶の維持 断絶の維持に関しては説明がない。もし内側円盤と外側円盤とで初期メタル 量が系統的に違っている違っていても、ガス拡散の結果断絶は、消し去られな いにしても、数 Gyr の間に均されるだろう。それにも拘らず、断絶は少なく とも 1 Gyr 昔までは残っていた。Simpson et al 1995 が提案した Rgc = 6 kpc の断絶は分子雲リングとそれに伴う腕の外縁に位置する。彼らは階段状の 分布はバーの存在による動径方向の掻き混ぜが原因であるとした。この考えは 10 kpc 段差とは別物である。ただ、内側と外側のガスを分離する力学的な境界 の必要性を指摘したことは重要である。内側帯と外側帯の差を示唆する証拠の 可能性が星団のスケール高の差にあるかも知れない。 |
高Z星団の存在 我々のサンプルは不完全で、内側帯には 1 Gyr より若い星団を含むが、図5 の星団 Z 分布は、外側古い星団のスケール高が内側星団と異なる可能性を示す。 Janes, Phelps 1994 は古い星団の Z 分布を調べて、スケ ール高= 325 pc を導いた。この値は若い星団に対する 55 pc と著しい対照 をなす。古い星団の年齢は 1 - 9 Gyr で、古い星団に Z 方向の拡散は働かない ので、銀河面での潮汐力による星団の分断か、衛星銀河の融合くらいしか、ス ケール高を説明できない。しかし、分断説だと高Z星団を薄い円盤種族の高Z テールとして説明しようとすると、円盤面近くに実際より多数の星団を必要と するので否定される。古い星団の高い Z 分布は過去10年間の継続する融合 現象を意味する。 もう一つ別の説明 Janes, Phelps 1994 の基本仮定は古い星団は全て同じ種族から生まれたと いうものである。したがって、彼らがスケール高を導く際には Rgc の違いは 問題にされていない。もし図5に見られるような Rgc = 10 kpc におけるスケ ール高の急変が本当であるなら、Janes, Phelps 1994 の値 325 pc は異なる グループのスケール高が合成されて出たものということになる。Rgc 10 kpc 内側の星団に関しては真のスケール高は 55 pc と 325 pc の間にある。 本来のスケール高は多分 55 pc に近い値で、それに銀河面潮汐力による星団 分断の結果多少の増加が加算されたものであろう。Rgc 10 kpc を越えた星団 スケール高は不明である。それは主に銀河面近くの星団数の情報が欠けている からである。銀河面から離れた星団を発見することは容易であるが、面内星団 は減光と背景星の多さに隠されている。それは Janes, Phelps 1994 の図7、 9に示される古い星団と若い星団の分布図を見れば明らかである。 もし外側帯において、若い星団のスケール高が 55 pc より大きい、 または古い星団の形成時スケール高が 55 pc より大きいなら、選択効果と 外側帯での低い分断確率と組み合わせて高Z星団の超過は低減可能である。 (論理がよく判らない。 ) これは依然として外側帯のスケール高が内側円盤のそれより大きいことを意味 している。これらが観測で確立すれば、内側帯と外側帯の力学的な差異がはっ きりするだろう。Janes, Phelps 1994 が提案した、外側帯での厚い円盤は 衛星銀河融合の結果と言う説も可能である。 ちょっと悲観的な結論 Wielen et al 1996 は星間物質のメタル量勾配を仮定して、太陽近傍星の メタル量を形成位置のタグ付けに使用できると考えた。しかし、ここで示した ように、内側と外側円盤でメタル量勾配が平坦だとこの手法は使えない。 何らかの別の方法が発明されない限り、太陽近傍で円盤の力学化学変化を調べ ることはできない。もしかすると {Fe/H] に対する [O/Fe], [Ca/Fe] から 内側星を分けられるかも知れない。厚い円盤で出来た星団はとっくに破壊されて しまい、その年代の外側円盤星団は太陽近傍円盤と何の関わりもない。 |