アブストラクトデータ領域南銀極 11.5 deg2 の 10,000 星と (l, b) = (37°, -51°) の 水がめ座 17 deg2 の 28,000 星 の V, B-V データを求めた。水がめ座の V - I カラーもここで論じる。それらから銀河系の構造パラメターと太陽近傍の 光度関数を決めた。 ミッシングマス 光度関数は Mv = +13 付近に広い極大を持つ。暗い方で下がるのは我々の以前の 結果と一致する。普通の星ではミッシングマスは説明されない。 |
厚い円盤成分? 銀河系楕円体の古い低メタル星は遠方ほど球に近い扁平楕円体の分布をしている。 この種族に加え、楕円体の内部には赤いターンオフを持つ、比較的高メタルの 古い種族が存在する。この種族の空間分布は明確には定義されていない。しかし、 それは「厚い円盤」と矛盾しない。これまでに提案された銀河系恒星分布モデル のどれもこれらのデータをうまく説明できない。 |
|
系外銀河での厚い円盤 銀河の密度分布と運動学がEggen,Lynden-Bell,Sandage の想定より複雑である という直接の証拠は、渦巻銀河の測光から来た。バルジを持つ銀河に「厚い円盤」 が見つかった。銀河面から数 kpc の楕円体は扁平な成分を有し、それは指数関数 的密度分布を示した。van der Kruit, Searle 1982, Jensen,Thuan 1982 それらの |
運動学観測は回転速度が銀河の主軸からの距離と共に滑らかに減少して行くことを
示した。ELS ではこれと反対に楕円体は回転しない。
銀河系の厚い円盤 我々は銀河系で直接に厚い円盤を検出した。銀河系では系外銀河より詳しい構造 が調べられる。 |

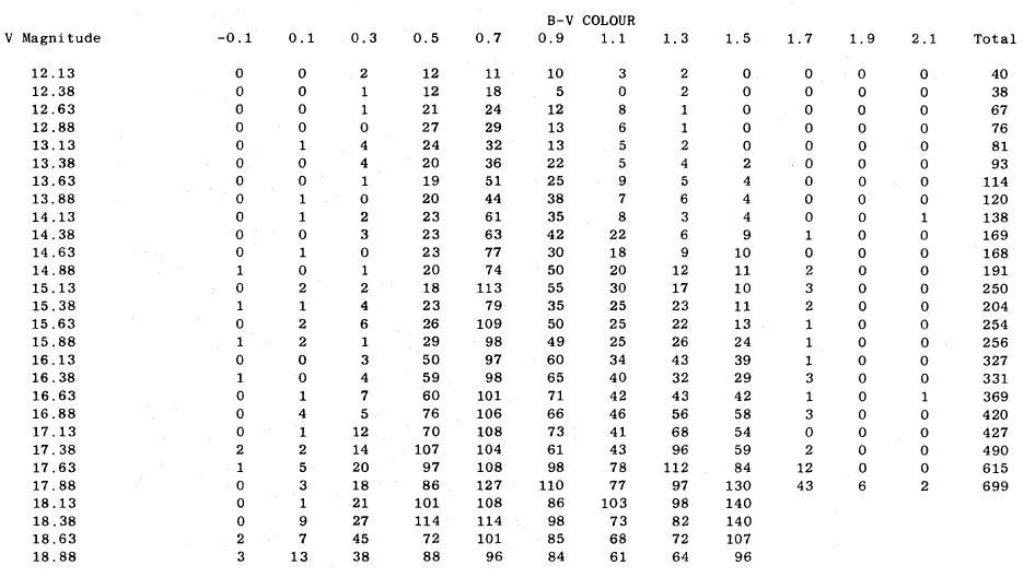
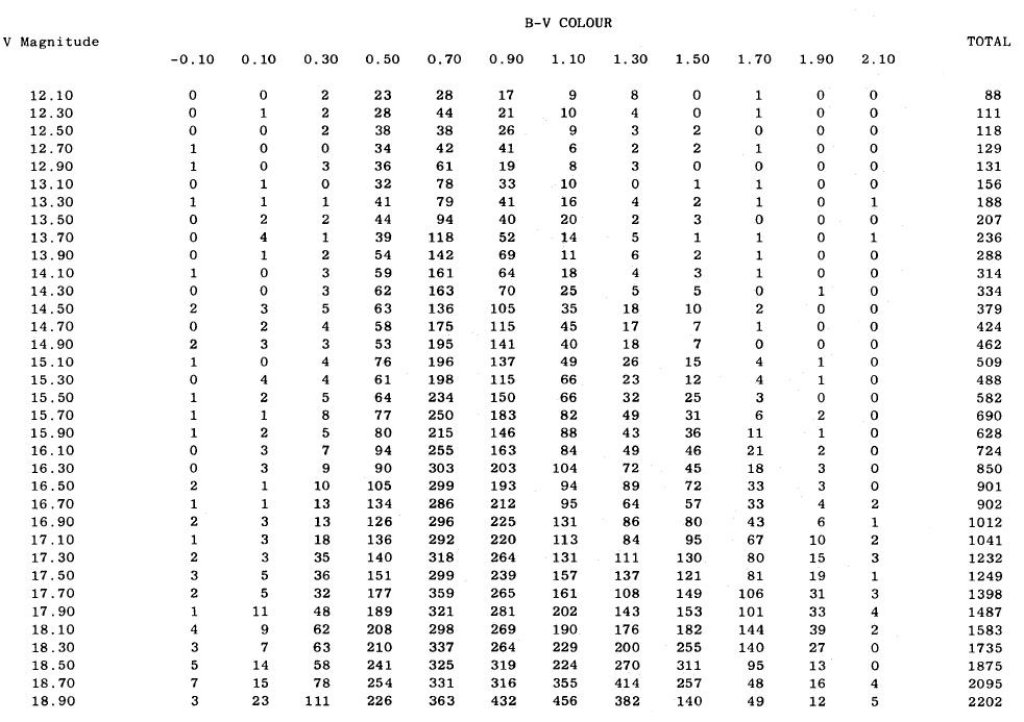
3.1.(l, b) = ( 37°, -51° ) 水がめ座方向17.14 deg2 から 33,445 天体のカタログが得られた。さらに 6673 個 の銀河も得られた。表3には 12 < V < 19 の星計数を載せた。3.2.(l, b) = ( 0°, -90° ) 南銀極方向水がめ座方向では V > 18, B-V ≥ 1.3 で、南銀極方向では V gt; 18 で 検出不完全性が始まる。銀河系の構造を調べる上で最も重要なのは、(1) B - V = 1.5, V ≥ 17 で赤いピークが現れて、双峰性が開始される。 (2) B - V = 0.4 での鋭い崖。 (3) B - V = 0 - 0.2 の青い星が極めて少ない。 (4) V > 16 では二領域の星計数間で大きな違いが現れる。 3.3.(l, b) = ( 37°, -51° ) の (V - I) 探査I観測上に述べた B - V 探査と別に I(IV-N + RG715) 観測も行った。これは、赤い星を B - V カラーに基づいて探すと不正確になるからである。こうして、 I ≤ 16.75 までは完全なサンプルを得た。 |
巨星の混入 見かけ等級が明るい星のほぼ全ては巨星であり、その多くが K 型であると 予想する。 Reid,Gilmore 1982 では我々はそれらのデータを単に考察から排除した。ここではやり方を変えて、光度 を詳しく決定する。 赤外観測 JHK 測光による光度クラスの分離は Reid,Gilmore 1984 で述べた。観測は AAT 3.9m と du Pont 2.5m でサンプルの最も赤い星について 行われた。 Na D 線 次の方法は,やや青い星に有効な Na D 線の強度である。そこで、Las Campanas 天文台において 71 星の分光を行った。こうして、V ≤ 16.5, V - I ≥ 1.5 の 完全サンプル 81 星に対して光度クラスの分類が可能になった。 巨星混入率は低い。 81 星中 3つは明らかに巨星であり、一つは多分準矮星、一つはデータが悪くて 不確実、残りの 76 星は明らかに矮星である。3つの巨星は皆 V ≤ 13.5 と明るく、 この明るさの星は他に二つしかない。それらの二つは近傍星 G1 46, G1 843 である。 この様なわけで、巨星の混入は V ≥ 13.5, V - I ≥ 1.5 では重要でない。 V ≤ 16.5, V - I ≥ 1.5 でも混入率はたったの 4 % である。 |
|
光度関数 これらの結果に基づき、V ≥ 13.5, I ≤ 16.75, V - I ≥ 1.5 の 完全サンプルを作った。これは巨星の混入を排除し、I等級限界より 1.5 等上である。 このサンプルから表7の光度関数を作った。これは太陽近傍での値を与えるように スケール高 300 pc の補正を施してある。この関数は Schmidt 1984 の光度関数とも 良く一致する。Mv = +13 付近に極大を持ち、低光度星がミッシングマスを担う 可能性を否定する。 |
 表7.太陽近傍での光度関数 |
4.1.(l, b) = ( 37°, -51° ) 水がめ座領域Tritton, Morton 1984 は我々と同じ方向を中心に 0.31 deg2 の B, V 測光を行った。サンプルは B ≤ 19.5 で完全な 601 星からなる。 共通する 456 星を比較した。色・等級星計数を比べると系統的なずれがある。 これは領域が狭く、標準星が少ないためであろう。重要な違いは、彼らの計数には B ∼ 19, B - V ∼ 1.7 付近にピークが現れることである。これが本当なら Mv ∼ +12 の M 矮星が太陽近傍に多数分布することを意味する。しかし、この 特徴は我々の I 探査に現れていない。 |
4.2.北銀極領域Weistrop 1972, 1976 の北銀極観測はカラーにエラーが付いていないので、 等級カウントだけを我々の南銀極データと比べる。 V ≤ 16 での一致はよい。 それより暗い方では 15 % の範囲で一致する。彼女の標準星は V = 16.5 より 暗い方では 6 個しか使っていず、それが不一致の原因であろう。 |
|
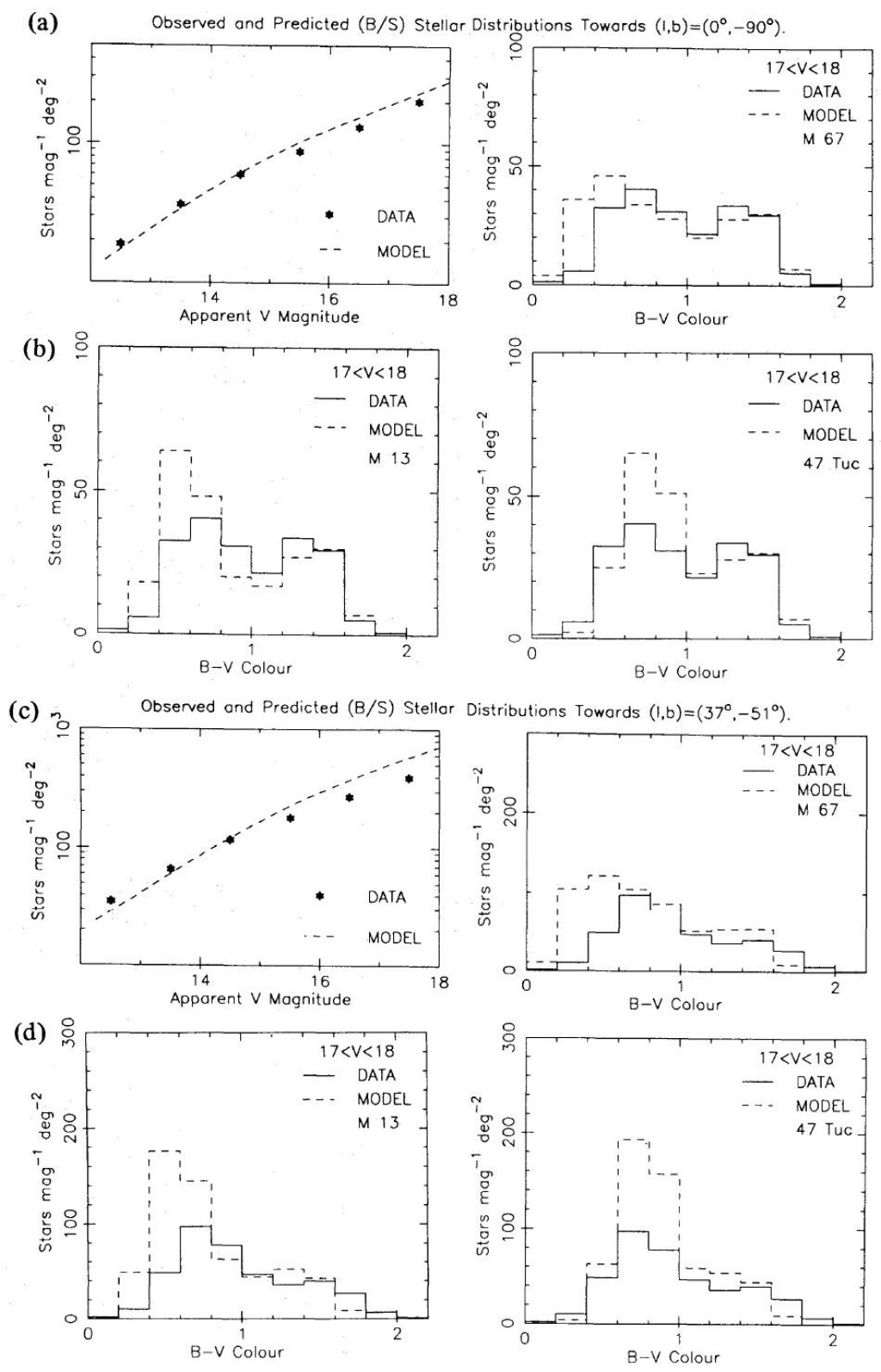
初期の銀河系モデル 銀河の構造に関してかなりの議論がある。 第1の方法は銀河系の構造を単純な円盤+楕円体と仮定し、平均メタル量以外の 恒星パラメターは同じとして星の分布を導く。このタイプのモデルは van den Bergh 1979, Gilmore 1981, Pritchet 1983 が始め、 Bahcall, Soneira 1980, Bahcall, Soneira 1984 は特に大規模なモデルを構築した。 第2の方法は、銀河系が同じハッブルタイプの銀河と類似の運動学、測光構造を 有していると考え、それを近似の出発点にするものである。これは Gikmore, Reid 1983 で提示されたモデルである。 ただし、これらのモデルのパラメターの決め方は一意ではなく、安定した 決定は困難であった。 系外銀河からの「厚い円盤」情報 銀河系と類似のバルジ対円盤比を持つ銀河の観測から、銀河面から数 kpc 以内 に高度に扁平な回転楕円体成分が存在することが明らかとなった。Kormendy, Illingworth 1982, van den Kruit, Searle 1982. Gikmore, Reid 1983 はこの成分を銀河系で初めて検出した仕事である。 モデル同士の比較 この第2手法の精神に沿って、我々は二つのモデルの成功した点と失敗した点を 比較検討したい。そのために使用するデータは 17 < V < 18 に限る。その理由は (1)Gilmore 1981 が行った等級ーカラー分布計算によると、この等級領域は 楕円体成分の主系列ターンオフに非常に影響を受ける。この領域のカラーはフィールド星の メタル量と年齢に制限を加える。 (2)論文を短くする。 図2と図3は単純モデルと厚い円盤モデルでの予想をデータと比べたものである。 単純モデルの予想は 1983年5月の日付のある B&S モデルのコンピュータプログラム で作りだされたものである。この版は Bahcall,Soneira 1981 の以前の予想とは最大 40 % 違っている。厚い円盤モデルは論文 VI で述べたものである。 | B&S 単純モデルはフィットが悪い 図2の単純モデルとの比較では、メタル量の高低を表現するため M67, M13, 47 Tuc の色等級図が使われた。B - V = 0.40 で青い端になるのは低メタル球状星団の ターンオフに対応しているが、分布関数の詳細は採用する色等級図に強く依存する。 Bahcall, Soneira 1984 は彼らの 1984 モデルが M 13 または M 92 色等級図を使って、銀極データを 20 % 以下の誤差でフィットできたと言っている。そのモデルはここで示したカウントに 対し 27 % の誤差を示し、カラー分布に対してはターンオフ付近でファクター倍の 違いを示す。b = -51° フィールドでは全楕円体カウントが2倍、カラー分布が B - V ∼ 0.8 付近で 3 倍違っている。 単純モデルは単純過ぎて観測に合わない Bahcall, Soneira 1984 はモデルにデータと 20 % 以内の一致を要求した。この要求に従うと、B&S が述べた 単純モデルは観測から退けられることになる。しかし、ここで重要なことはある 特定のモデルが適切かどうかではない。大体丸い楕円体ではデータとモデルの乖離が バルジより下を見た時の方が銀極方向より大きいことが大事である。これは楕円体が モデルが仮定したより扁平であることを意味する。実際、 b = -51° 方向の 一致はもし楕円体の b/a を 0.55 にするとぐっと良くなる。 Bahcall, Soneira 1984 が強調するように、そのような扁平モデルは銀極の暗い星計数と両立しない。従って 第2の重要な結論は、単純モデルの一組のパラメターでは観測と矛盾するである。 修正のため、単純モデルに軸比が連続的に変化するようにしたり、もっと複雑な 幾何学形状を考えるのは単純さの精神に反する。 単純モデルの光度関数は間違っている 厚い円盤の存在を確認する前に、もう一度強調しておきたいのは厚い円盤と単純モデル の類似点と相違点である。最も大きな違いは楕円体に適用される光度関数である。 単純モデルは太陽近傍の円盤光度関数を楕円体にも使っている。Gilmore 1983 IAU Coll. 76, p197-, p221- で述べたように、この選択が誤っている二つの理由がある。 (1)最近の星形成が起きていない古い種族の光度関数の観測結果(例えば Da Costa 1982)は主系列ターンオフで勾配の変化を示している。 (2)恒星進化モデルもその結果を支持する。 したがって、準巨星光度では主系列先端より光度関数が低下するはずである。この点は 重要である。というのは現在議論しているカラーと光度は正に主系列先端を越えたところ だからである。 |
|
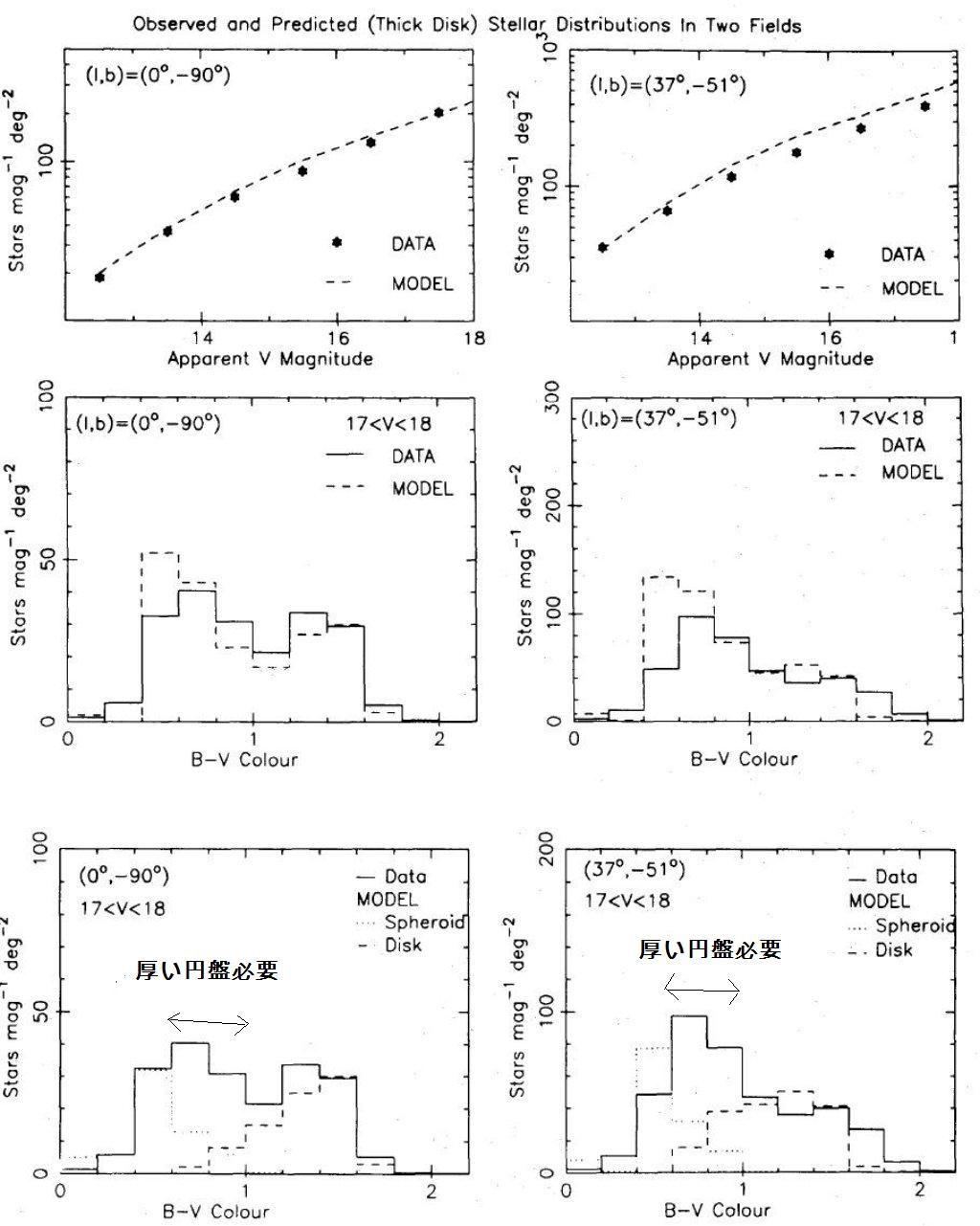
厚い円盤モデルは球状星団光度関数を採用 厚い円盤モデルは、その結果、球状星団光度関数を厚い円盤と楕円体に採用した。 Gilmore 1984 を見よ。 平坦で高メタルな楕円体成分の付加 第2の相違点は、厚い円盤モデルでは平坦で高メタルな楕円体成分を新たに付加した ことである。この成分の運動学的及び化学的な証拠は、 Gilmore 1984 に詳述した。以下では測光での証拠を下に述べよう。この新しい成分は太陽付近での 2 % を占めている。指数関数型円盤と考えるとスケール高が 1.5 kpc, R1/4 楕円体と考えると軸比 b/a ∼ 0.3 である。この成分を「厚い円盤」 と呼ぶ。 二つのモデルの間の最も重要な類似点 二つのモデルの間の最も重要な類似点は、 (1)楕円体軸比が b/a ∼ 0.8 で規格値は 0.1 - 0.2 % である。 (2)薄い円盤のスケール高、光度関数は良く似ている。 第3成分の必要性 第3成分が必要な理由は図3に示されている。球状星団光度関数を楕円体 成分に適用した二成分モデルのフィットを見ると、0.6 ≤ B - V < 1.0 に星を供給するために第3成分が必要なことが明らかである。すると、もう二つの 結論が導かれる。 (1)第3成分、厚い円盤、が 17 < V < 18 カラー分布に必要。 (2)この種族は赤いターンオフを持つ。 この種族を表現するのは例えば 47 Tuc のような高メタル球状星団である。 |
外側楕円体は丸いモデルだけで十分 Bahcall, Soneira 1984 が強調したように、高銀緯 2 領域では V > 20 の暗い星計数はかなり丸い 低メタル楕円体で十分良く説明される。厚い円盤は従って楕円体外側ではとても 薄くなっている必要がある。その結果、空間速度大とか低メタル量という特徴で 選ばれてきた楕円体トレーサー、つまり RR Lyr, 水平枝星、低メタル球状星団は 系外銀河の運動学に用いられるラインの強い楕円体星を代表しないことである。 厚い円盤が回転していれば 我々の銀河系に見られる非常に低メタルでほぼ無回転の楕円体星と系外銀河の回転に より平坦化している楕円体の存在の間にある矛盾は、もし、厚い円盤が回転してい るなら解消する。現在、これを実証するための運動学的な観測が進められている。 同様に、フィールドの赤い水平枝星が多数存在するであろうことも予言される。 新しい銀河モデル このように、データとの比較から出てきたモデルは、良く知られていた薄い円盤 と複雑な楕円体からなる銀河系である。楕円体は形が平坦で赤いターンオフ を持つ種族と、青い(B-V ∼ 0.4)ターンオフを持つ丸い種族から成る。 上のような要求に加え、運動学的、化学組成データと一致する必要がある。 とくに、楕円体の大規模回転と速度分散テンソルの要求。 |
|
これまでの結果 これまでの結果は、 (1)太陽付近の光度関数は Mv ∼ +13 付近に極大を有する。光っている星の 密度は運動学から決まる密度には不十分である。 (2)低メタルで銀河中心距離(8 - 15 kpc)と共に次第に丸くなる楕円体成分 がある。ターンオフカラーは [Fe/H] ∼ -1.5 球状星団との値と近い。 この成分は速度分散が大きく、殆ど回転していない。観測との比較では以前得られた パラメターだと多すぎる星を予想してしまうことがわかった。 | (3)星のカラー分布は第3成分の存在を予想する。これはターンオフが赤く、 もっと平坦な空間分布を示す。この種族の特徴はまだ不明確である。これは しかし、[Fe/H] ∼ -0.7 の 47 Tuc のような球状星団の色等級分布と 矛盾しない。それらは赤い水平枝星を持つと考えられる。この種族は古いと 考えられるがどのくらい古いかは不明である。 |