Luminosity Functions of Disk and Halo Populations in SA 51, SA 57, and SA 68

　３．光度関数と密度分布　

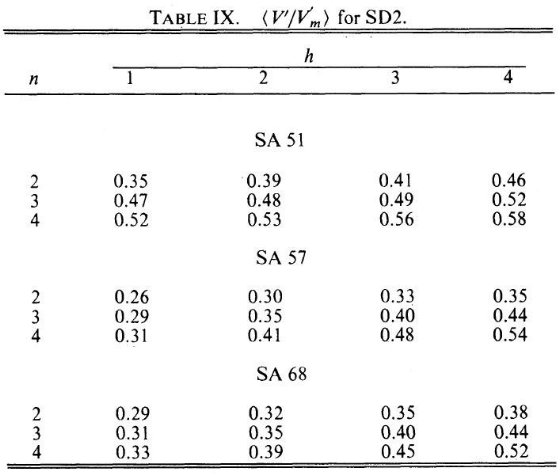
３．１．種族 I 系列　 　Schmidt 法の改良　 　 Chiu 1980a では、Schmidt 1975 の方法 Schmidt 1975 の方法を改良し、星の一つ一つにその星がある種族 P、ある光度クラス L に属する 確率 p(L,P|Hv,B-V) を与えた。ここに Hv は整約固有運動である。近傍密度は Σ[p(L,P|Hv,B-V)/V'max] で与えられる。 　密度則　 　V' の計算には密度則 D(R) が必要であった。ここでは 密度則に、 (ω0/ω)nexp(-z/z0) の形を仮定し、次の二つの密度則を検討する。 ケースＡ：n = 2, z0 = 300 pc. z 方向速度分散 σz = 20 km/s ケースＢ：n = 4, z0 = 500 pc. z 方向速度分散 σz = 33 km/s 強調したいのは、このやり方は仮定した密度則から光度関数を導いていることである。 (V'/V'max) 法を使うどんなモデル（上の A, B を含め）でも、もし密度則とそれから 導かれる光度関数を使えば星計数は再現できる。したがって、星計数だけからあるモデル がよいという結論は出せない。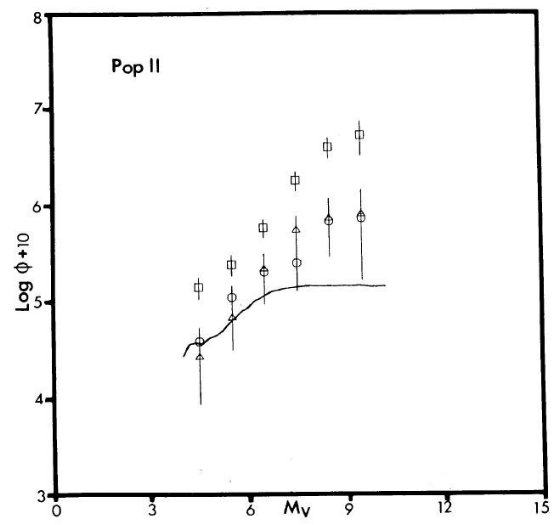 　各領域での光度関数　 　図１a-c に光度関数を示す。四角はモデルＡ，丸がモデルＢ、実線は Wielen である。最も明るい Mv = +2.5 は種族 I 巨星と準巨星からの寄与である。最も 暗い側では白色矮星からの寄与が加わっている。注意しておくのは光度関数の等級 毎に異なる距離からの星が寄与していることである。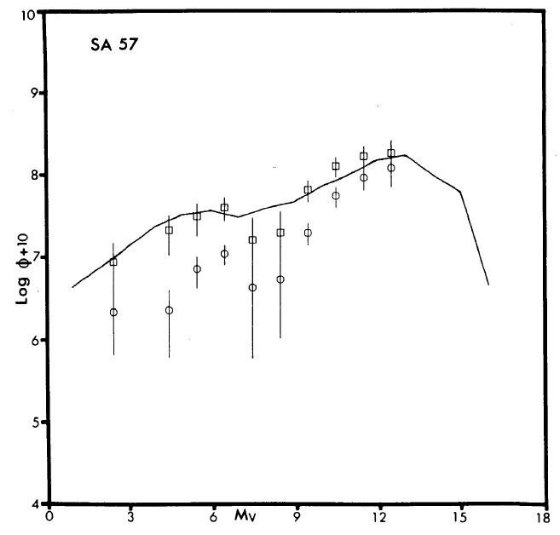 図１b. SA 57 からの種族 I 星の光度関数。最も明るい星は巨星と準巨星。 　　　　実線は Wielen 光度関数。四角＝モデルＡ、丸＝モデルＢ

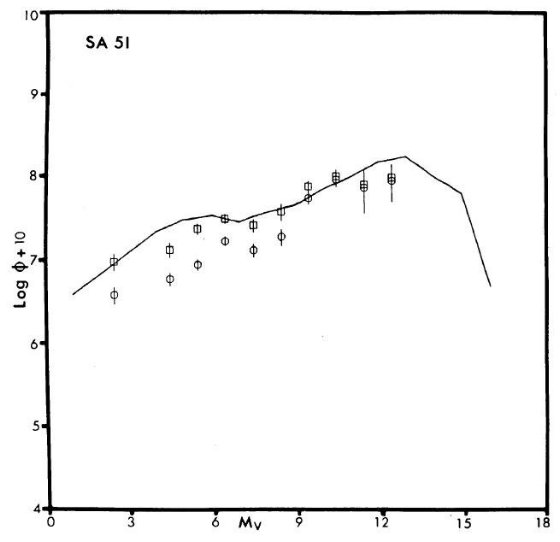
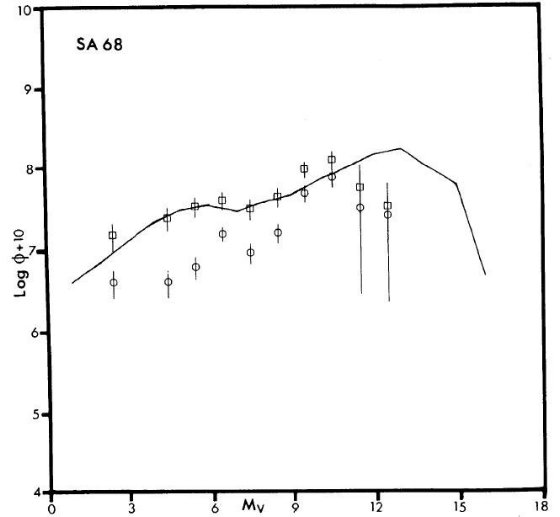
図１a. SA 51 からの種族 I 星の光度関数。最も明るい星は巨星と準巨星。 　　　　実線は Wielen 光度関数。四角＝モデルＡ、丸＝モデルＢ 図１c. SA 68 からの種族 I 星の光度関数。最も明るい星は巨星と準巨星。 　　　　実線は Wielen 光度関数。四角＝モデルＡ、丸＝モデルＢ

種族 II 光度関数　 　種族 II の光度関数を求める際に、楕円体の軸比もフリーパラメターとして 考える。表９には　(V/Vmax) テストの結果を載せた。0.4 < ⟨V'/V'max⟩ < 0.6 を許容範囲としても、軸比 h=1, 2 と n = 2 のモデルは全て不適当と なる。n = 2 が拒否されたことは Ostriker, Peebles, Yahil 1974 が提案した マッシブハローとは違うことを示す。軸比 h が 3, 4 というほど大きいことは驚きで ある。n = 3, h = 4 の組み合わせは３領域すべてで適当な ⟨V'/V'max⟩ を与える。 表９．準矮星の ⟨V'/V'max⟩

図２にはこの組み合わせで得た楕円体種族の光度関数を 四角＝SA 51、丸= SA 57、 三角= SA 68 で示した。目立つ特徴は SA 51 の光度関数が 6 倍くらい大きいこと である。楕円体光度関数としては、これを除いて、SA 57 と SA 68 の平均を採る ことにした。最終的な光度関数はここに求めたものを Mv = 4 - 10 等に、Schmidt のそれを規格化してから Mv = 10 - 12 等に使用することとした。 図２．準矮星の光度関数。四角＝SA 51、丸= SA 57、三角= SA 68。実線は Da Costa による NGC 6397.

種族 II 星の結合光度関数　 　得られた種族 II 星の結合光度関数は Mv = 7 - 12 で種族 I 光度関数とよく 似た勾配を示すことが判る。Mv = 4 - 12 の種族 II 星空間密度は (4-5) × 10-4 pc-3 である。種族 I では Mv = 4 - 12 の外に約 30 % の星が存在するので同じ補正を施し、種族 II 星の全空間密度は 6 × 10-4 pc-3 である。種族 I は 0.11 - 0.13 pc-3 なので、規格値は 0.5 - 0.6 % である。

図３．種族 II 星の結合光度関数。上は Wielen 光度関数。