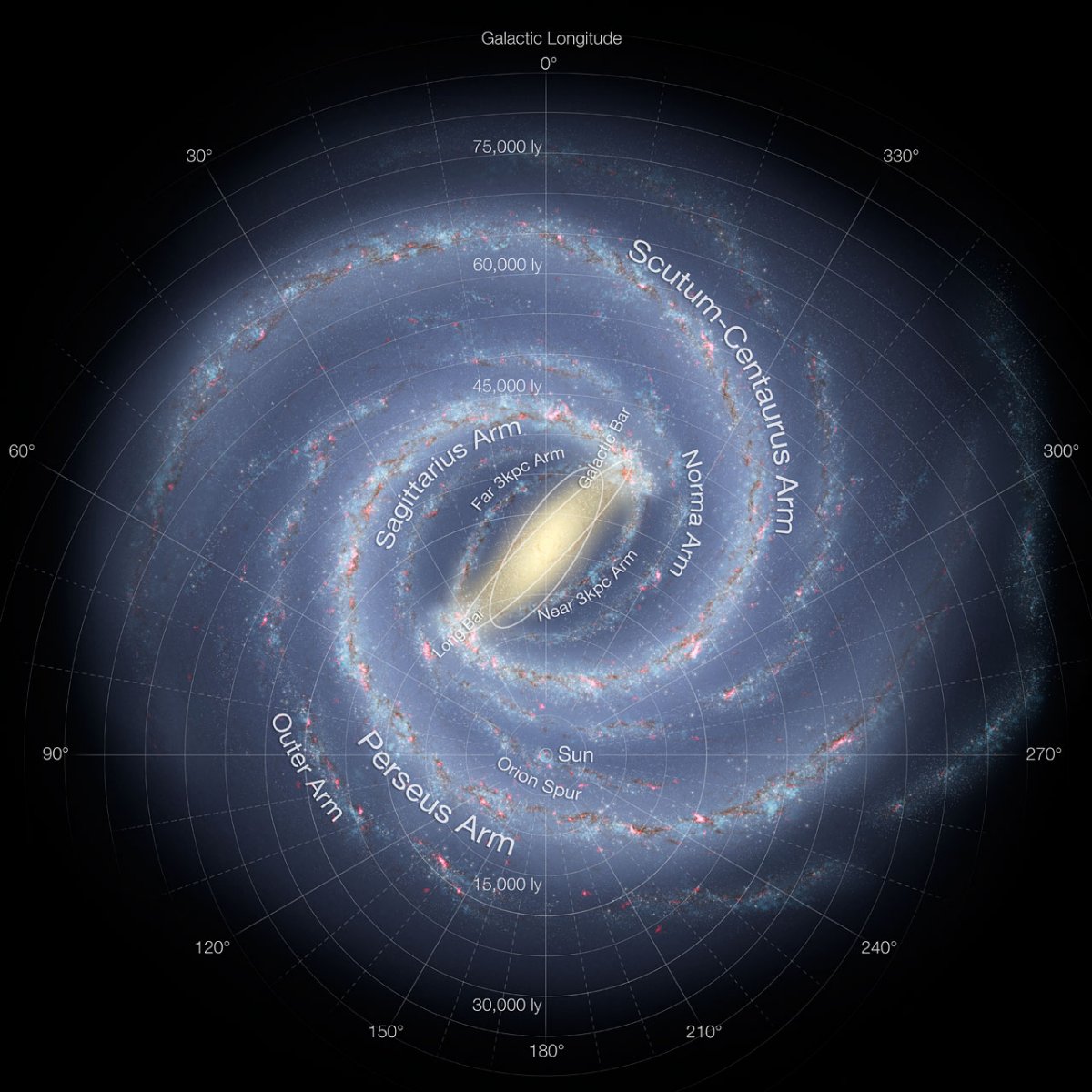
| 測光と分光データに星距離を組み合わせると3Dダストマップが作れる。 SDSS と APOGEE DR14 を用いて、太陽から 7 kpc, 銀河面から 100 pc 以内の ダスト分布を求めた。累積物理量でなく局所物理量であるダスト分布を導く 方法にはガウシャンプロセスに基づいたノンパラメトリック法を採用した。 | この方法は、3D 空間内の点の間でダスト相関(?) をモデル化し、事前に定 める関数形に拘束されず任意の形の変化を捉える。結果として得たマップは 渦状腕らしき特徴が見られた。これは何の仮定も置かずに、ダスト分布に腕 構造を見出した最初の例である。マップには既知の大きな分子雲が見え、 それらの幾つかは距離が不定であった。 |

|
これまでの3D減光マップ ダストマップに関し重要な研究の一つは Schlegel, Finbeiner, Davis (1998) による IRAS と COBE を用いたダスト柱密度 2D マップである。より詳しい 2D マップが Planck Collaboration et al 2014 により発表された。 3D マップの試みとしては、 Marshall et al (2006) の銀河系モデルと近赤外色超過を用いた研究が重要である。Schlafly et al 2010 は星のカラー分布の左端を主系列ターンオフカラーと考えて SDSS-III の観測範囲の赤化を測った。Sale (2012) はヒエラルキー型 ペイジアンモデルを多色測光モデルに適用して、星のパラメタ―と減光を 同時に決める方法を開発した。Sale et al 2014 はこの方法を IPHAS データに適用して北側銀河面の 3D 減光マップを作った。 類似の確率論的な方法は Hanson, Bailer-Jones 2014 によって、 Bailer-Jones 2011 の方法に基づいて、有効温度と減光を決めるのに使われた。彼らは ベイズ統計を用いて、減光と有効温度の間の縮退を説明し、UKIDSS と SDSS から |b| > 30° 高銀緯帯の 3D 減光マップを作った。Green et al 2014 は Sale 2012 と似た方法で測光データから減光を求める方法を開発した。 Schlafly et al 2014 はその方法を用いて δ > -30 の減光マップを 作った。Green et al 2015 は PAN-STARRS1 と 2MASS から銀河系3象限の 3D 減光マップを作った。最近 Green et al 2018 はこの方法を改良し、新しい 減光曲線と PAN-STARRS1 の新しいデータをくわえて最新版を発表した。 |
新しい傾向 これらの方法の欠点は各視線方向を他と独立に扱っていることである。 そのため、結果に断裂が現れる。Vergely et al 2010 はデータギャップを克服 するため平滑核を導入し、太陽近傍のダストマップを作った。類似の方法は Lallement et al (2014) は類似の方法でやはり近傍マップを作った。彼らは Capitanio et al 2017 で改良し、 Gaia TGAS データの距離情報と Diffuse Interstellar Band (DIBs) の SDSS/APOGEE スペクトルからの色超過を取り入れ、Pan-STARRS1 赤化観測 の粗い減光マップを出発点にして、マップの精密化を行った。 Sale, Magorrian 2014 は減光の対数 log A をガウスランダム場と考えて 減光マップを作った。 ダストで腕が見えるか? 減光マップに渦状腕が現れた例はない。これは正確な距離が使用されていない ことと、ダストマップ導出法の裏にある仮定に誤りがあることが原因である。 今まで引用した研究は累積量である総減光量を示していた。このため局所量 の表示が出来なかったのでないか。さらに、研究の多くは個々の視線方向を隣と 独立に扱い、隣からの情報を使えなかった。 ノンパラメトリック法による解析 本研究では複雑な構造を捕えるためにノンパラメトリック法を用いる。さらに、 ダスト密度を直接マップする。等方ガウス過程を用いて、ダスト点の空間相関を 考慮し、視線方向の人工構造のない連続的なマップを作る。 Rezaei et al 2017 ではこの方法を詳しく述べた。その後第2章に述べる改良を 加え、APOGEE-2 データを処理した。 |
|
入力データは個々星の3D位置とその減光量である。 |
解析法の理解は難しそうで省略する。 |
|
巨星の選別 APOGEE-2 は近赤外高分解能分光探査である。APOGEE DR14 から log g = [0.5, 3.5] の基準で巨星を選んだ。その (Teff, log g, [M/H]) を 恒星進化モデル http://stev.oapd.inaf.it/cgi-bin/cmd PARSEC と参照して 距離と色超過を求めた。 (Teff, log g, [M/H])から MJ, MH, MK 各星に対し、星パラメタ―較正 PARAM (Holtzman et al 2015) を用いて Teff, log g を求める。等時線上で観測した (Teff, log g ) に最も近い 点を探し、MJ, MH, MKs を決める。 減光量は AKs = 0.528 E(J-Ks) で決め、距離 d は d = 100.2(Ks-MKs)+5-AKs で求める。詳しくは、 Schultheis et al (2014) を見よ。位置精度は 30 % 程度である。 レッドクランプの選別 Bovy et al 2014 は APOGEE データから、 カラー・メタル量・表面重力・ 有効温度空間内でレッドクランプ星を選別する方法を見出した。 その幅の狭さから距離精度は 5 - 10 % である。その減光は Majewski et al (2011) の Rayleigh-Jeaans Color Excess = RJCE 法から計算した(Bovy et al 2014)。 APOGEE DR14 には RC 30,000 星の距離と減光が載っている。 最終サンプル 巨星とレッドクランプのカタログから、|Z| < 100 pc の星を選んだ。 レッドクランプカタログには Ro = 8 kpc, 太陽の銀河面高度 = 25 pc と 仮定して(Bovy et al 2014)求めた Z が記載されている。我々は同じ仮定を 採用し、巨星の Z を計算した。また、レッドクランプの距離精度に揃えるため、 巨星でも距離精度 5 % 以下の星に限定した。その結果、レッドクランプは 5000 星、巨星は 16,000 星が残った。図1に両方の X-Y 分布を示す。巨星が より遠方まで広がっていて、より大きな減光値まで伸びていることが判る。その 差は特に第1象限と銀河中心方向で著しい。 ハイパーパラメタ― 我々はこれらを別個に扱った。レッドクランプ星も巨星も星同士の間隔は大体 200 pc であった。そこでこの値をセルサイズに採用した。相関距離 λ = 1000 pc とした。対応する θ はレッドクランプで 9 10-9 pc-2, 巨星で 6.5 10-9 pc-2 である。 ガウス過程の事前共通平均密度(?) ρμ は 1.2 10-4 pc-1 と計算される。注意しておくが、相関 スケール長 λ は我々のマップの限界分解能ではない。我々の分解能は サンプル星の間隔に応じてもっと小さい。実際、相関長さは相互作用する2点 間距離の最大値を見なすべきである。 |
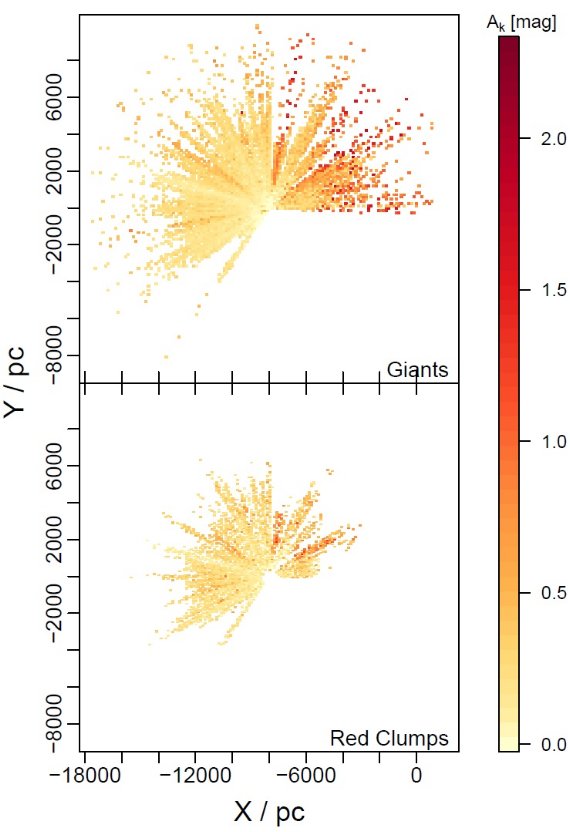 図1.入力恒星位置の X-Y 分布。Z = [-100, 100] pc.太陽位置=(-8000, 0), 銀河中心=(0, 0). 上:巨星。下:レッドクランプ星。点のカラーは AK。巨星は 7 kpc まで、レッドクランプ星は 5 kpc まで。 |
|
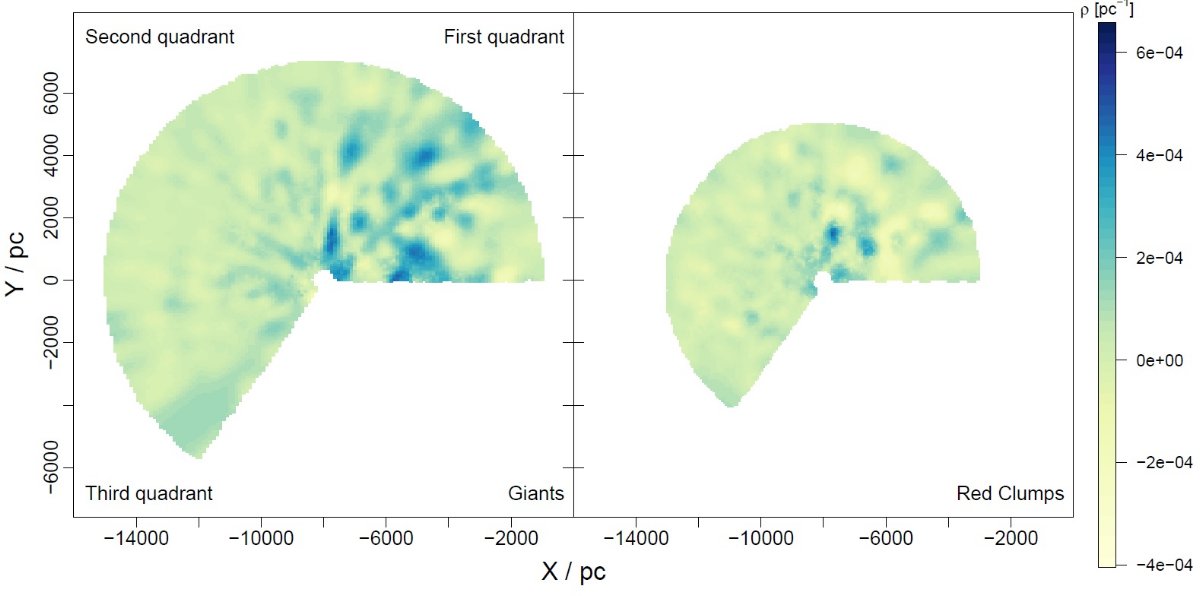
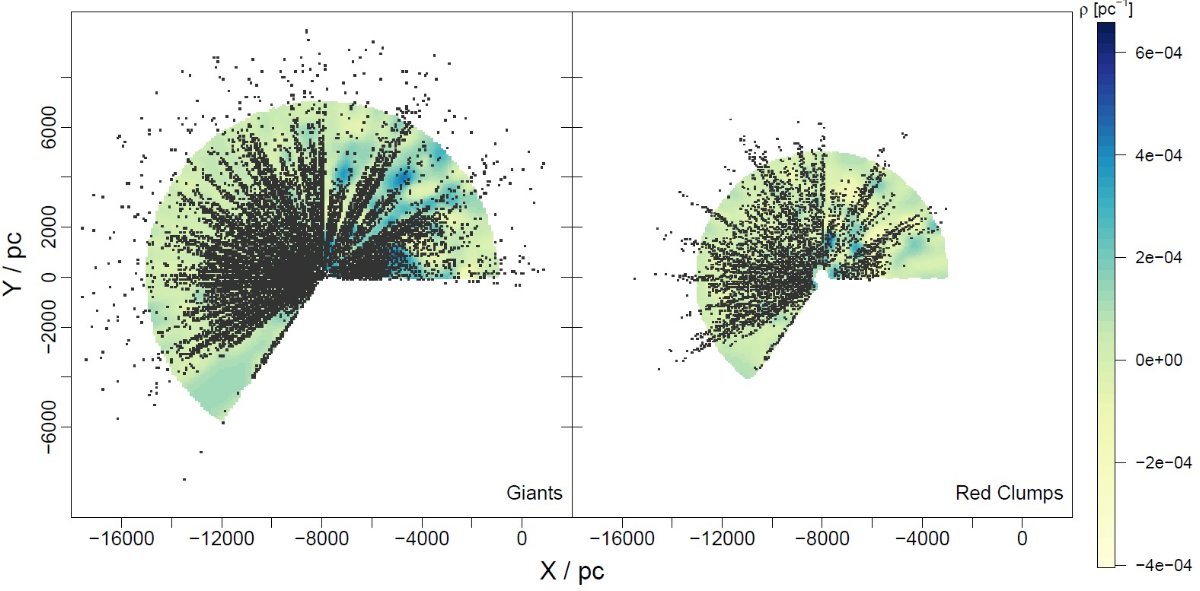
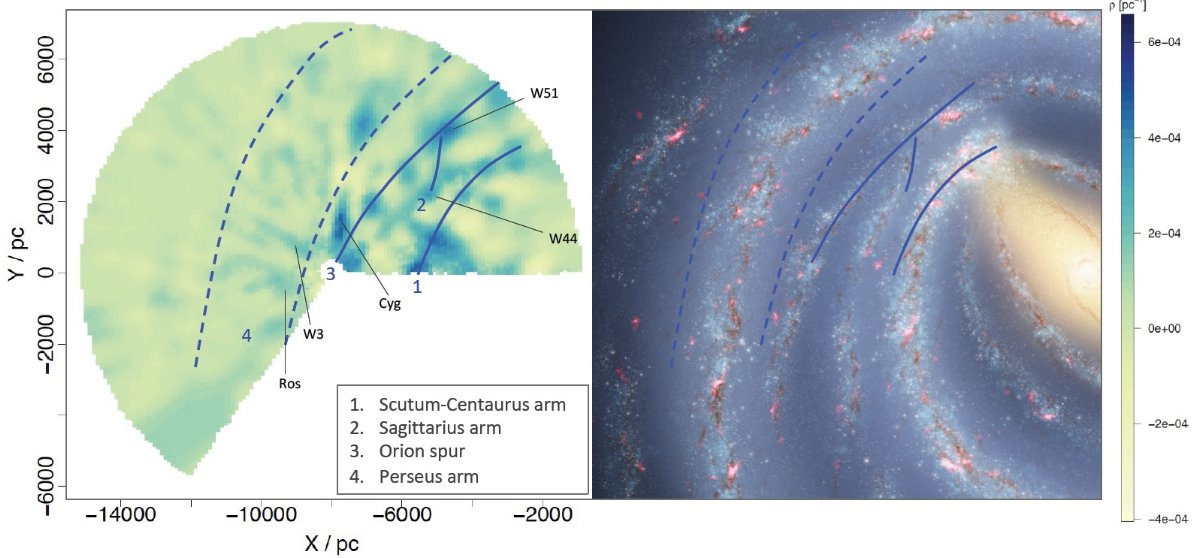
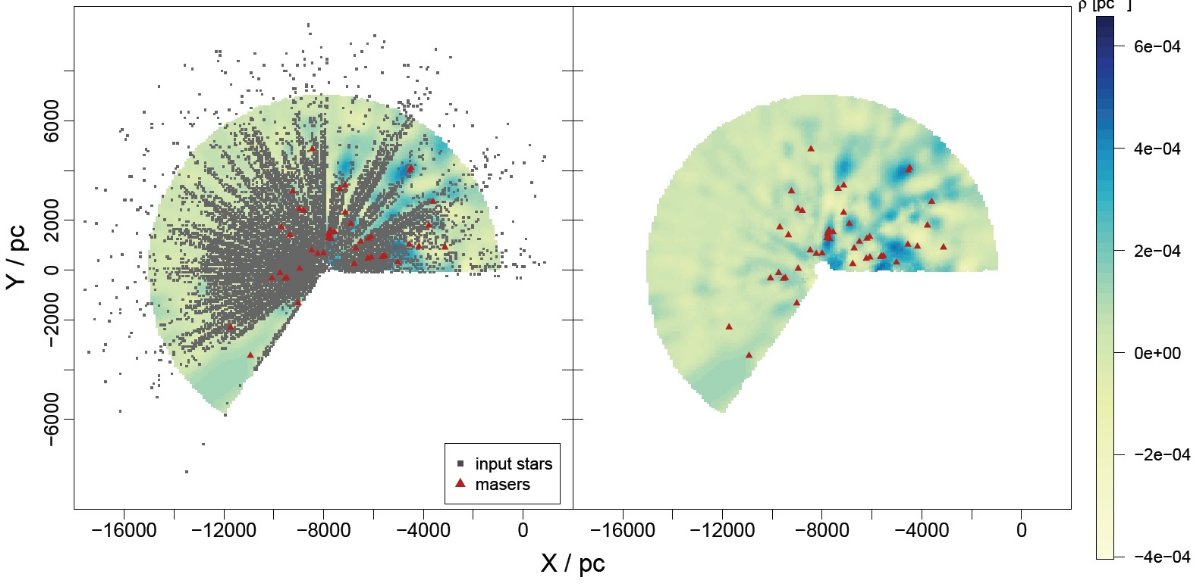
第1象限での不一致 図2は巨星(左)とレッドクランプ(右)によるダストマップを示す。 どちらの図にも多くの高密度雲(> 1.2 10-4 pc-1 と構造が見える。第2、第3象限ではどちらの図も似た構造を追っている。 しかしながら、第1象限では両者の差は劇的なほどに広がる。その原因は 図3を見ると明らかである。レッドクランプ星の数が第1象限で少ないので ある。この場合、事後確率は事前確率に圧倒されてしまうのである。しかし 巨星は第1象限にも多数が存在するので、そこでもダスト量の不定性は小さい。 星不足によるギャップ 図3に見られる注目すべき点のもう一つは、図左下に入力星不足による 溝が存在することである。近距離で溝の両側の星の間隔が相関距離 1000 pc 以内の所では予想値は近くにある星の存在に影響される。より遠方では相関が ゼロに落ち、予想値は入力されるガウス過程事前値の平均に近くなる。同じ 規準がレッドクランプを使った第1象限の外側銀河系マップにも適用される。 スピッツアー想像図との相性 以上の理由からこの先は巨星マップに焦点を当てる。第1象限の高密度雲は 渦状腕の予想位置で弧状に連なっているように見える。そこで、それらをつな いだ。図4左で、第1象限に連なる雲を結んで3本の青線を引いた。しかし、 第2象限では高密度雲が広く広がり、明瞭な線が見えない。そこで、線の代わ りに帯を引いた。図4右にはそれらの曲線と帯をスピツアー描画の上に重ねた。 この想像図はスピツアー観測に基づいていることを述べておく。他の銀河 系渦状腕想像図はモデル依存的で、相互に大きく異なっている。一方このスピ ッツアーマップは星の観測に基づいていて、銀河系モデルにはあまり依存しない。 その点我々の研究と似ている。 我々が予想した第1象限の腕はスピッツアー想像図と割とよく似ている。特 にオリオンスパーがよい。スキュータム・ケンタウルス腕の一部も良く合う。 我々の斜線帯はペルセウス腕を丁度載せている。これは Baba et al 2018 が GAIA DR1 に基づいてペルセウス腕が壊れつつあると述べたことに合う。 巨大分子雲 腕以外に既知の巨大分子雲も検出した。図4に示してある。文献によると W51 ブンし雲は 5-8 kpc である。(Parsons et al 2012) 我々のマップでは 5.5 kpc となり、 Sato et al 2010, Russeil 2003 の値と一致する。W44 はサジタリウス腕に付随するように見えるが、距離 3 kpc である。 白鳥座分子雲方向には 1.5 kpc と 2 kpc に二つの GMC が見える。 OB アソシエイションの白鳥座Xまでの距離は 1.7 kpc (Schneider et al 2006) とされている。W3 (2 kpc) と Rezetta GMC (1.5 kpc) にもやや低めの超過が 認められる。 |
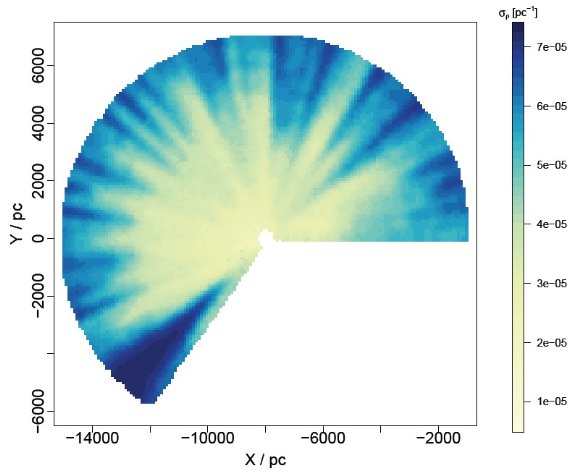 図5.ダスト密度予測値の標準偏差。紺青=大きな不定性=星の数が 少ない領域に現れるようだ。 誤差 図5には予想誤差を示す。一般には距離と共に星の数が減るため誤差は大き くなる。誤差を入力データ図3と比べると、誤差の大きな領域が入力星間の ギャップが大きい箇所で発生することが確認できる。図4から分かるように、 サジタリウス腕の位置は太陽近くになると確定できなくなった。これは 銀河中心方向で正確な測定が欠けているためと、南天データが無いためである。 オリオンスパーと並行して、比較的高密度の線状の領域が存在するが、これが サジタリウス腕の一部のようだ。しかし図5はこの領域のエラーが比較的大き いことを示しているので、今回この構造は腕に加えなかった。 |
|
モデルは円盤と腕の形にどんな関数形の仮定もしていない。このマップ上の どんな構造も、背後のダスト密度を推定させる入力データにガウス過程からの 平滑化の仮定を適用して得られたものである。腕構造により強い制限を加える ためには速度情報が有用であろう。将来, GAIA, 4MOST, WEAVE からのデータ がより詳細な距離、固有運動を数百万の星に対して与え、腕のより正確な位置 を得ることが出来る。その時には星の速度と密度超過からの腕とダストの腕の 位置が一致するかどうかが分かる。 CO と HI 観測からの l-v 図 Dame, Hartmann, Thaddeus (2001) は銀河系の渦状腕をなぞっている。ガスとダストはよく混ざっているので、 同じ腕構造を表しているはずである。しかし、ガスの視線速度から求める距離 は大きな誤差を含む。この問題を克服する試みは様々になされ、腕に付随する と考えられる星形成域の距離 Wiene, et al 2015, Whitaker et al 2017 |
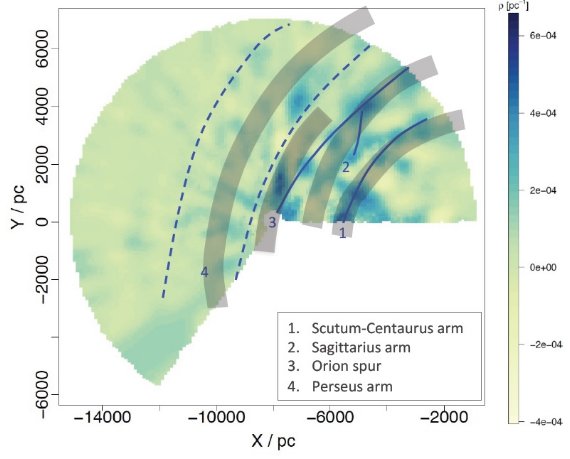 図7.図4と同じだが、 灰色帯= Reid et al 2014 の渦状腕を重ねた。帯の 幅は位置の 2σ に相当。 |

|
|
|

|
|
|

|
|
|

|
|
|

|
|
|

|
|
|
