| 銀河の後期進化の間進行する星形成を持続させる上で星からの継続性マスロス の役割を調べた。恒星質量 Ms 銀河に対して、観測される Ms-星形成率関係の 進化から導かれる星形成史に様々な初期質量関数を仮定して、標準的恒星進化 モデルのカスロスを合わせて用いて、全星種族からの総マスロスを計算した。 | 我々のモデル恒星からのマスロスによる再生ガスは現在の晩期型銀河で進行 中の星形成を維持するに十分である。星からのマスロスはしたがって、観測か ら導かれる比較的低レベルのガス落下率と円盤銀河で見られるかなり速い星形 成との間の対立を取り除くものである。冷たいガスの落下率が評価されている 銀河に対しては、星形成によるガス消費率と落下率との差を星からのマスロス が埋めることを直接に示す。 |
|
冷たいガスの供給源は? 星形成銀河では 2 Gyr の内に系内のガスを食べ尽くす。しかし、星形成銀河 は全てのレッドシフトで観測される。理論モデルでは、星形成銀河の大部分で 冷たいガスの降着がその星形成率を決定する。加えて、宇宙における中性水素 の量は、非常に速いガス消費速度に拘わらず、過去100億年の間に 50 % し か落ちていない。つまり、冷たいガスの供給が連続的に補給されているのである。 HVCsと衛星銀河 HVCs=高速中性水素雲の観測によると、星形成の 10 - 20 % は HVCs により賄われている。衛星銀河の降着も大きな寄与をなす。 コロナガス これまでのところ、銀河円盤にガスを供給する仕組みは不明である。円盤を 囲む高温コロナガスがミクシング等の仮定で冷却速度を上げて円盤に落ちてく る機構も提唱されているが、不確実度が高い。 |
ガス消費のタイムスケール 不確実な経路を調べる前に、AGB 星からのガス供給を調べてみよう。星形成銀河 と異なり、MW は Gyr の間に星質量の 2 % のガスが供給されるだけで済む。 星から星間空間への質量注入は Roberts 1963 を嚆矢とする。Sandage 1986, Kennicutt et al 1994 は、再生ガスが円盤銀河におけるガス消費タイム スケールを伸ばすだろうと述べた。 Blitz (1997) は MW においてマスロスガスの寄与が大きいことを示している観測に注意を向 けた。それにも拘わらず、最近の研究では一般には、星のマスロスはガス供給源 として考慮されていない。 銀河形成 銀河形成シミュレイションでは最近マスロスを取り入れるようになった。その 結果は銀河形状に大きな影響を及ぼすというものであった。 Agertz et al. (2011) Schaye et al. (2010) 総マスロス この研究の目的は、星形成の燃料補給にマスロスがどのくらい重要か、観測 からの拘束を調べることである。特に、星間空間へのマスロスによるガス注入 が、多くの近傍銀河で現在の星形成を維持するのに十分であることを実証する。 銀河内でのマスロスを評価するには、SSP のマスロス率時間変化を与えるマス ロスモデルが必要である。また、恒星集団の年齢分布を与える星形成史も必要 である。 |

|
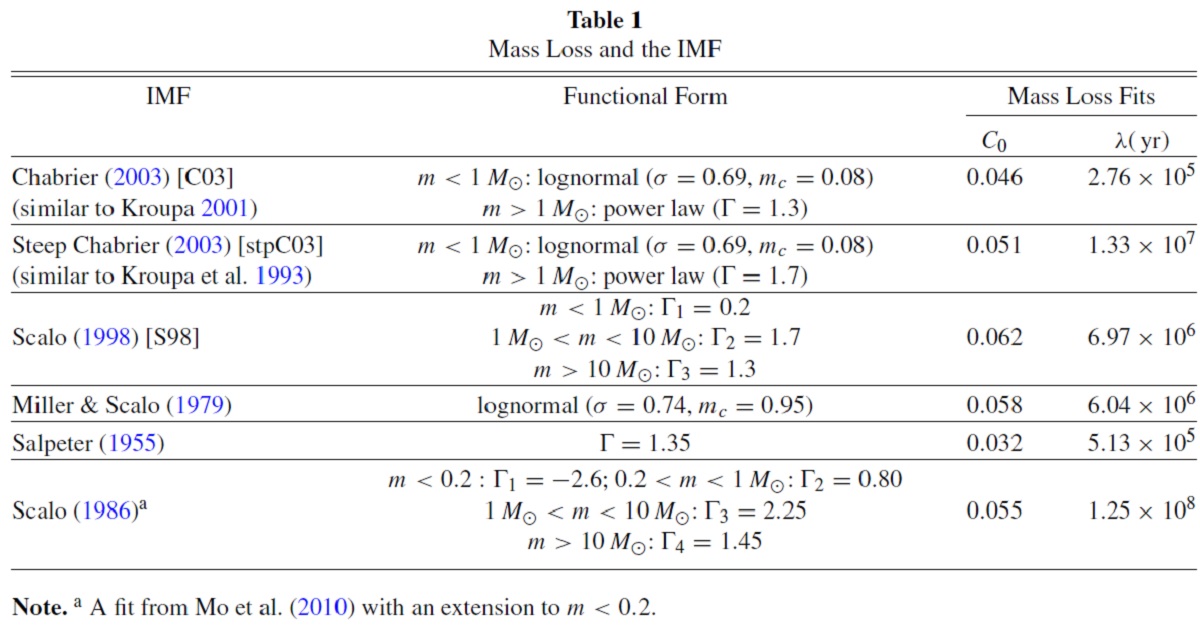
SSP からの総マスロス量 SSP の星から放出された質量 =M(>MTO) - 残骸M(>MTO) である。恒星進化経路からのマスロス率をSSPからのマスロスの評価に使う。 しかし、MS TO 年齢(Raiteri96) と IFMR (Kalirai08) を使い、Agertz11 のようにして出した値でも、最初の 2 Gyr 内では 5 - 10 % 低い程度で ほぼ同じである。 色々な IMF 表1には様々に提案されてきた IMF をまとめた。 dN = ξ(lnM) dlnM で質量関数 ξ(lnM) を定義すると、簡単な例として、 ξ(lnM) ∝ M-Γ や
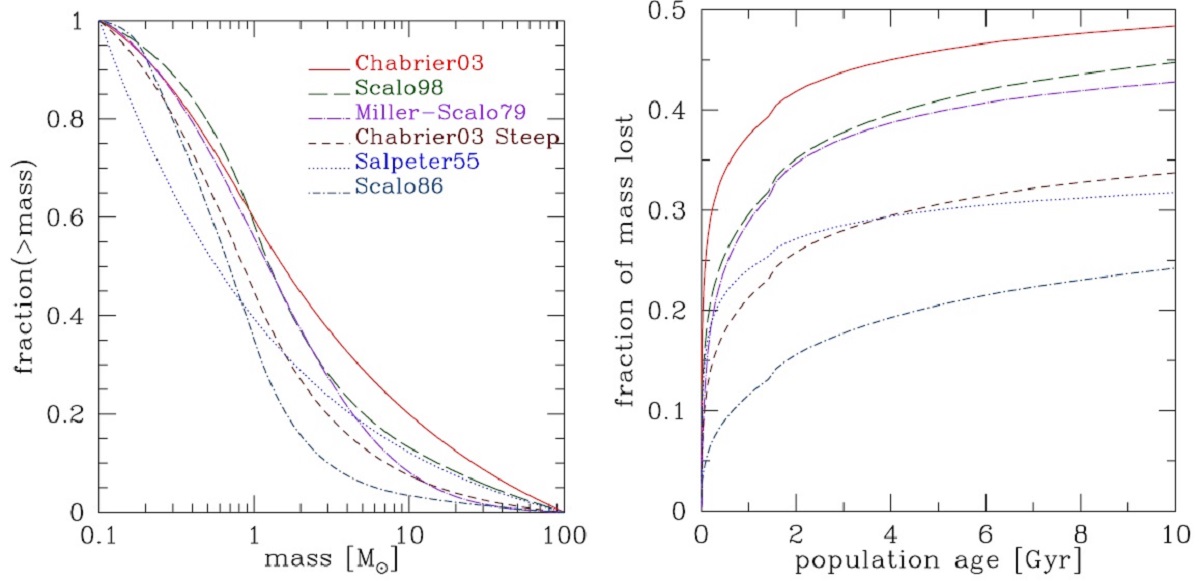
がある。それらの各自に対応する累積質量比を図1左に示す。それらの間の相 対比はM = 1 Mo で 20 %, それより大きい方ではファクター 2−3まで大き くなる。 総マスロス量に対する IMF の影響 図1右には、SSP からの累積マスロス量の時間変化を、初期SSP総質量で規格 化して示す。これらは、パドヴァ恒星進化モデル http://stev.oapd.inaf.it/cgi-bin/cmd を用いて、Flexible Stellar Population Synthesis (Conroy,Gunn 2010) で 計算した。 (IFMR を使った引き算でなく、各質量の 進化経路に沿ったマスロス率を積分する方法。 ) |
図を見ると、SSPからのマスロスは大部分が初めの 2 Gyr で起きることがわかる。
しかし、その後もゆっくりしたマスロスが長く続く。その様子は IMF により異なる
が、ファクター2程度である。しかし通常の銀河で考えられる IMF Kroupa07 の
範囲内では 30 % 以下の差に収まる。
IFMR のメタル依存は弱い。 Jungwiert01 は累積マスロス量 f(t) を以下の式で表した。
Co と λ の値を表1に載せた。個々の星の進化段階ごとのマスロス率は メタル量の影響があり、 ≤4 程度の散らばり(Mauron,Josselin10) を有するが、 重要な量は、 IFMR の観測である。Kalirai08, Marigo07 によると、IFMR のメタ ル量依存は弱く、Z = 0.1 Zo での IFMR は Z = Zo と変わらない。したがって、 SSP マスロスの不確定性の大きな原因は IMF である。 C03 IMF を採用 IMF の包括的議論は Bastian10 を見よ。今回、我々はよく使われる Chabrier03 (以降 C03)とその急勾配版 stpC03 を用いる。stpC03 は M < 1 Moでは C03 と同じである。しかし、M > 1 Mo で、サルピータ勾配より 0.35 急になる。 この二つで観測から示唆される IMF の範囲は大体カバーされる。それらには、 低質量での平坦化 Miller, Scalo (1979), Kroupa93 と高質量での勾配の範囲の広がりが含まれる。 サルピータは低質量星が多すぎる ただし、今回 Salpeter55、Scalo86 の IMF は検討から外した。低質量星が多すぎる からである。この先、基準 IMF として C03 を用いる。 |
3.1.星形成とマスロスの歴史SFR-M* 関係Olver10 は 70, 160 μm サーベイから、星形成銀河の SFR-M* 関係を調べ た。図2には、M* = 1010.75 Mo 銀河の赤化進化を示す。静謐銀河 を含む研究もそれに合う。 (静謐でも同じとは、よく分からない。 SFR が違うから静謐なんじゃないのか? ) z > 1 では SFR-M* 関係の規格化と勾配の不定性は大きくなる。 IMF の形が進化している可能性もある。 しかし、幸いなことに、z > zbreak = 2 での星形成は、 今回対象とする晩期型銀河の z = 0 でのマスロスにはあまり影響しない。さらに、 M* < 1011 Mo の晩期型銀河では z < 1 で星形成が起きているので、z 大での SFR の 進化はあまり重要でない。本研究では z > 2 では SFR = 一定とした。 SFR ∝ M*β+1 と近似した時、z < 1 では -0.5 < β < 0 である。β が z と共に下がる、一定、上がると 諸説は収束していない。われわれは、β = -0.25 = 一定と仮定する。 つまり、SFR ψ - M* 関係 を
ここで、晩期型銀河には α = 3.4 を採用する。ψ はある z での SFR 中間値で、特定の銀河の SFH とは区別される。Ao = 2.8 Mo/yr である。 zbreak < z < 6 では α = 0 とし、最初の星は z = 6 で爆発的に生じたと考える。これらの星は M:o の数パーセントにしかならない。 |
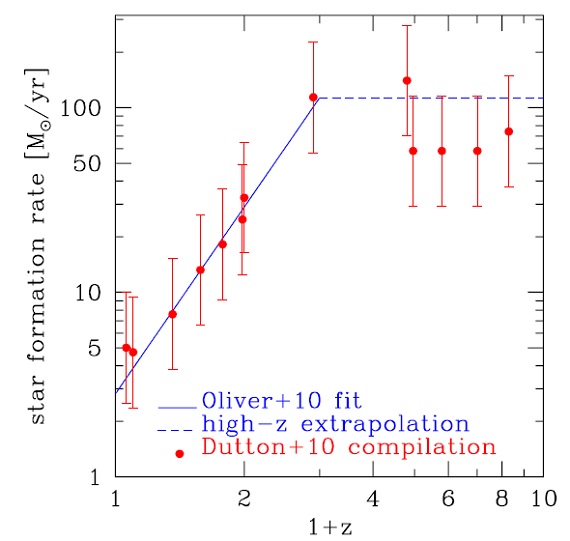 図2.M* = 1010.75 Mo 銀河における SFR-M* 関係の規格化。 |
|
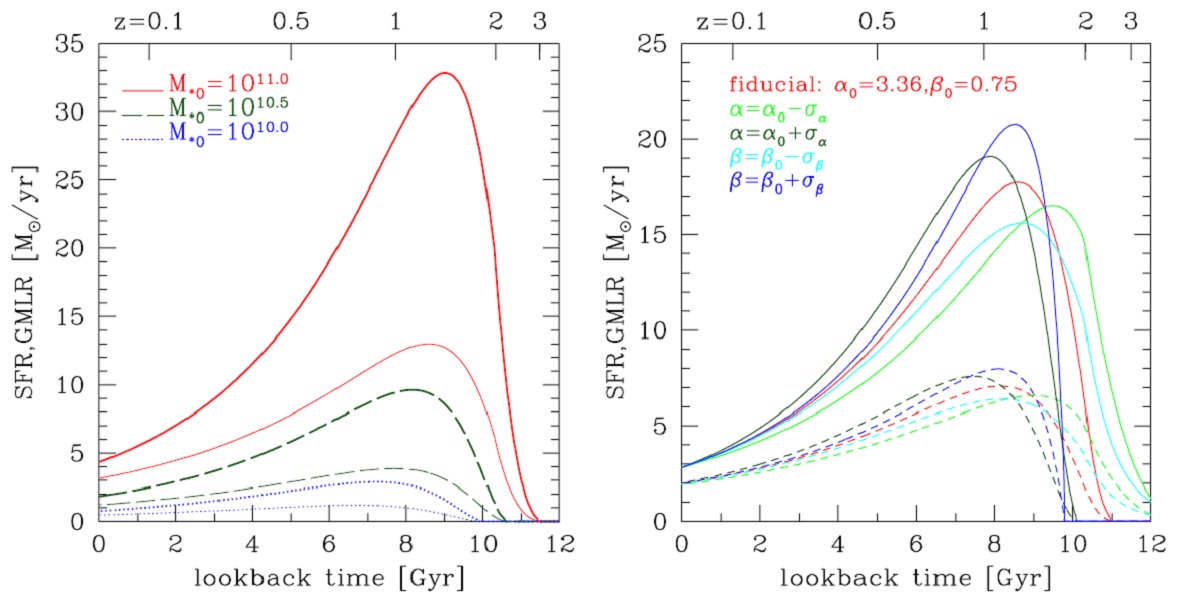
マスロス率と星形成 銀河の GMLR = Global Mass Loss Rate は、SFR と マスロス比率 fml との畳み込みで与えられる。式1参照。 GMLR(t) = ∫SFR(t')fml(t-t')dt' (3) 銀河の恒星質量の進化は、 dM*(t)/dt = ψ(M*, z) - GMLR(t) (4) t は振り向き時間なので、境界条件は t = 0 で M*(t=0) = M*o である。 ここに、ψ(M*, z) は式2で与えられる。星形成史は、 SFR(t) = ψ(M*(t), z) (5) |
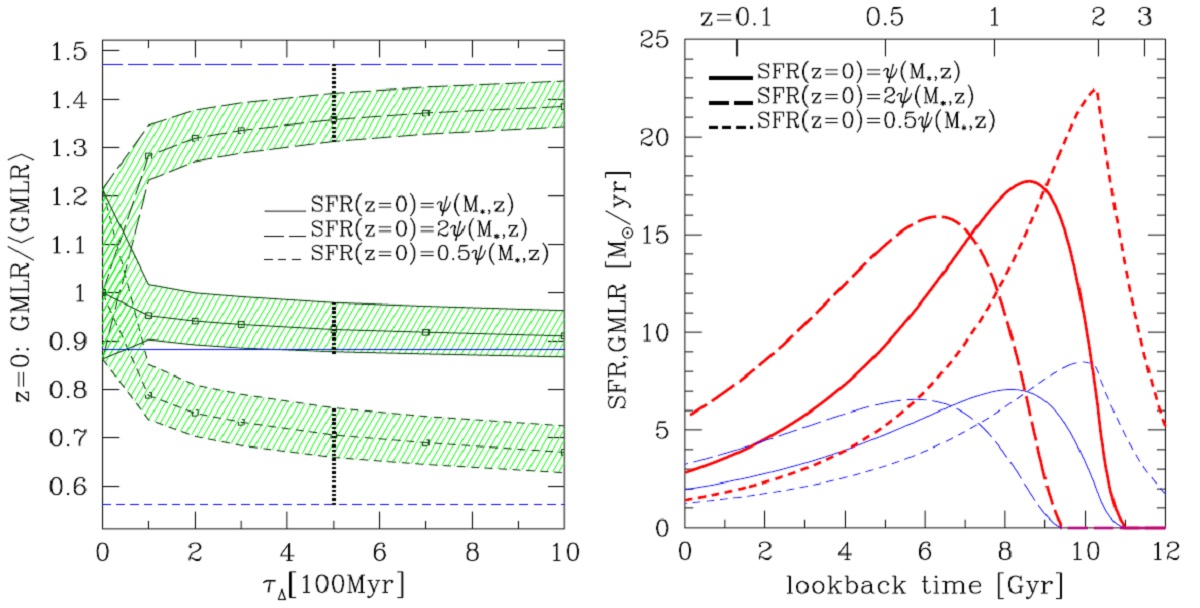
SFR(t) と SMLR(t) の逐次解 M*(t) の時間変化は(4)式の様に、GMLR(T)で決められるし、一方 GMLR(t) (3) 式のように、それより過去のM(t') 全体で規定される。したがって、両者は 逐次近似で解かれる。具体的には、初めはマスロス=ゼロとして、積分から M*(t) を求め、次にそれを (3) 式に入れて GMLR(t) を決める。第2段ではそれを (4) 式に入れて M*(t) を...と収束するまで (4), (3), (4), (3) ...を繰り 返すのである。こうして求めた SFR(t) と SMLR(t) を図3左にプロットした。 図3右には SFR-M* 関係のパラメター α, β の影響を示す。 |
|
実際の SFR の散らばり ある銀河の SFR が式2で記述されるメディアン SFR ψ(M*,z) の周りで 期間 τΔ の間大きさ σ* のずれを 経験する。散らばりの大きさはログノーマルと仮定する。こうして、ψ(M*,z) に N(t, τΔ, σ*) を掛けて、ずれた 星形成を表現する。 図4左 散らばりの効果を図4に示す。M* = 1010.75 Mo 銀河の場合に、 (この先全く分かんないんですけど ) |
図4右 図4右には τΔ = 14 Gyr とした時の星形成史とマス ロス史を示す。SFR(z=0) が低い場合には高 z で SFR が高くなる。それは現在 の銀河星質量を一定としているからである。この押し返しはまた、低 z で低い マスロスとなって表れる。というのは、星種族は若い時に多くのマスロスを行う からである。しかし、SFR(z=0) が低くなってもマスロス率は、即時放出近似で 仮定去れるようには、それに比例はしない。 というのは、古い種族がマスを放出し続けるからだ。実際には図4の低 SFR(z=0) ケースの場合、マスロスと星形成のラインは非常によく似ている。これはそのよ うな銀河ではマスロスが星形成のほぼ全ての原料を賄っていることを示している。 逆に、SFR(z=0) が高い銀河では同じレベルの星形成を維持するのにその原料と してより少量のマスロスで済む。 (ここも分かんない。 ) |
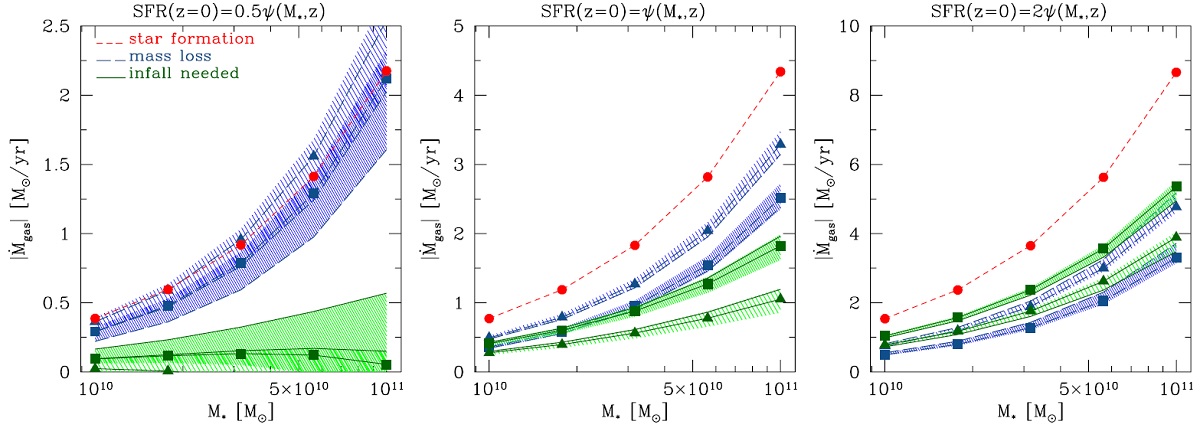
4.1.z = 0 マスロス降着ガス図5に、IMF に C03, stpC03 を仮定した場合の、現在のマスロス率を銀河 星質量の関数として示す。SFR とマスロス率との差を埋めるために外部ガスの 降着が要求される。それは図5での斜線部で示される。 (銀河内のガス量=一定が要求されている? ) 図5中央=stpC03 INF の場合 図5の中央は全恒星質量範囲に渡って、マスロスが降着をしのいでいること示す。 stpC03 INF の場合でも、マスロスが星形成のかなりを占めるが、降着ガスが SFR の 45 - 60 % を占める。 図5右= 図5両側は 現在の SFR が SFR-M* 関係から ± 1σ* 離れた場合の星マスロスを示す。左側は SFR が中間値より低かった場合で、星 からのマスロスが C03 でも stpC03 IMF でも外部ガス降着より大きい。右側は SFR が高かった場合で、SFR を維持するためにより多くのガス降着が必要で ある。 stpC03 IMF に対しては降着ガスは SFR を維持するのに必要なガスの 60 % に寄与する。 C03 IMF では 40 - 50 % になる。 4.2.再生期マスロス率が星形成率の半分を上回る見返り時期を図6に示す。この時期は 再生時期と呼んでよいだろう。その時期から先ではマスロスが星形成で消費さ れるガスを補う。図6を見ると、低 SFR 銀河では z = 0.7 - 0.9, メディアン で z = 0.3 - 0.6, 高 SFR で z = 0.05 - 0.2 が再生時期となる。 この時期は IMF に鋭敏である。 |
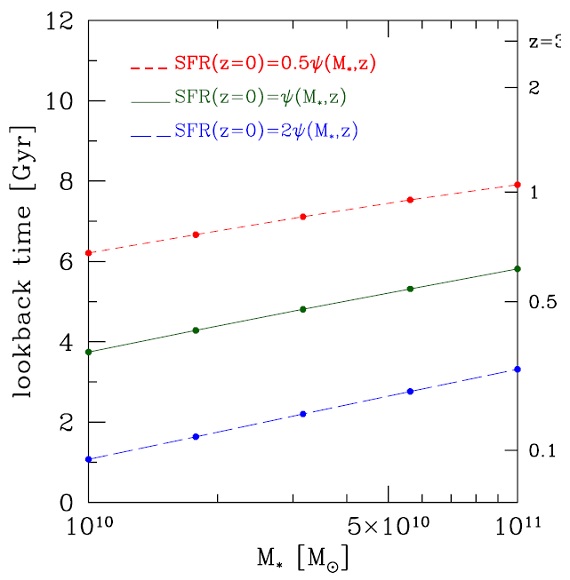 図6.マスロス率が星形成率の半分を上回る見返り時期。 C03 IMF 仮定。 短(長)破線=SFR(z=0) の 16 パーセンタイル(84 パーセンタイル)銀河の例。 実線=メディアン SFR-M* 関係の銀河。 |
|
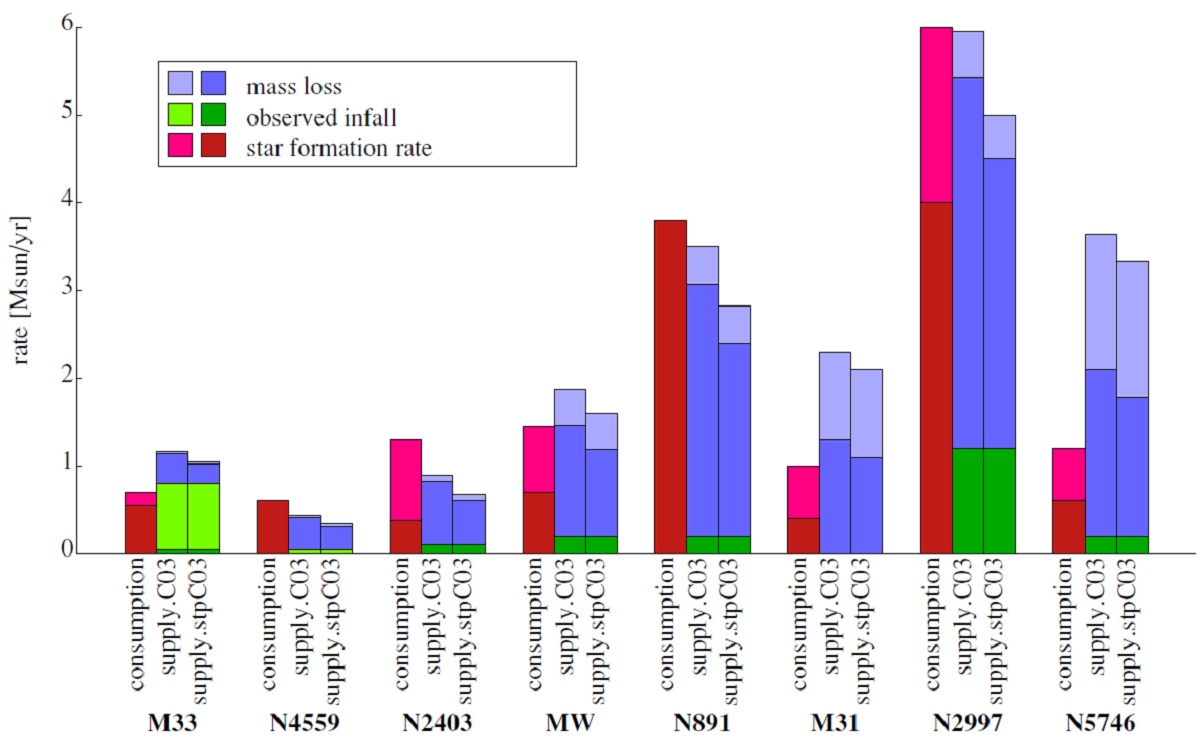
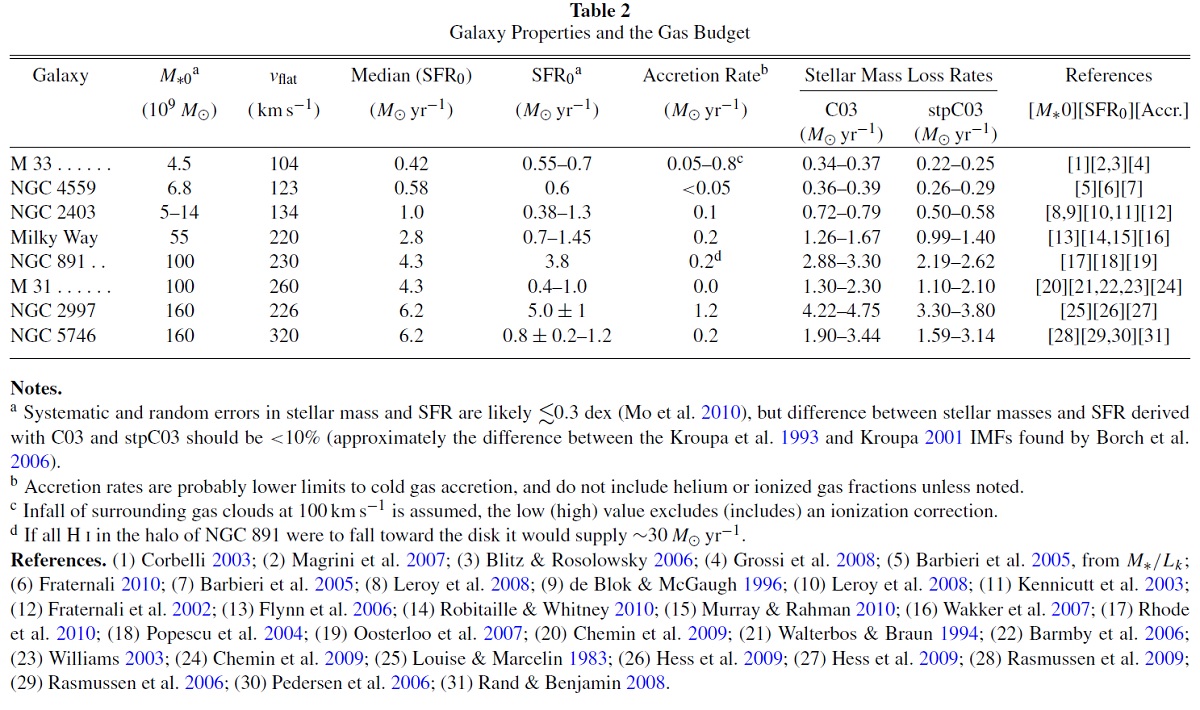
図7=ガス収支 冷たいガスの降着が観測できる銀河は数個しかない。しかし、得られた結果は 全て、母銀河における SFRs に比べるとかなり低い。これは多くの研究でガス 不足の懸念として表明されている。表2と図7には、降着ガス量が観測されて いる銀河におけるガス収支を示す。そこでのマスロス量は SFR(z=0) と M*o からの観測的拘束を入力して、モデル SFH によって現在の マスロス率を計算した。 マスロス+降着=SFR 表と図を見ると、マスロス+降着=SFR がほぼ成り立っていることが判る。 勿論、ヘリウム量の補正、電離ガスの割合などが降着ガス観測には必要で、 それらが不定性を生んではいる。 |
AGB マスロスの観測 Jackson et al. (2007a) Jackson et al. (2007b) Matsuura et al. (2009) Srinivasan et al. (2009) は LMC, Wolf-Lundmark-Mellote, IC 1613 などの近傍矮小銀河内の AGBs 観測 から AGBs マスロスの総計を求めた。その結果 AGBs からは SFR の 10 % (LMC), から 50−100 % (WLM, IC 1613) が供給されていることが判った。超新星や赤色 巨星からの追加ガス補給を考えると、これらの銀河で進行中の星形成に使われる ガスのかなりをマスロスが供給していることを示す。 |
|
マスロスが星形成を維持 異なった質量毎に観測的に決められた星形成史に恒星進化コードを合わせて、 晩期型銀河では星形成の材料の供給源としては星からのマスロスが最も重要で あることを示した。WLM, IC 1613 のような近傍銀河における星からのマスロス 観測はこの結論と合う結果を与えた。 重水素の問題 重水素は星に取り込まれると簡単に壊れる。したがって、星間空間での重水素 量は星間ガス内でマスロスによる再生ガスの割合に拘束を与える。しかし、 その観測結果は方向により差が大きく、またダスト吸着効果もあり、不確実で ある。 |
早期型銀河 早期型銀河ではマスロスがかなりなのになぜ星形成が起きていないのか? 楕円銀河の星から放出されるガスは高温希薄なハローとすぐに混ざり合う ためではないか?円盤銀河では星が一緒に回転する星間空間にガスを放出 するので上手くいくのであろう。 シミュレイション シミュレイションにマスロスを取り入れる必要がある。 |