Miller79

The Initial Mass Function and Stellar Birthrate in the Solar Neighborhood

Miller, Scalo

1979 ApJS 41, 513 - 547

　アブストラクト　

　太陽近傍での初期質量関数(IMF)と星形成史を調べた。現在の質量関数は光度関数から決めた。関連する観測量全て、光度関数、質量・光度関係、スケール高、非主系列星の補正、主系列星の光度増加、と不確定性を議論した。観測された総質量は力学質量=オールト質量とひどく矛盾はしない。従って、局所的に "隠された質量" を想定する必要はない。
　星形成史に対する主な拘束は、主系列星寿命が円盤年齢と等しくなる質量で、導いた IMF が非物理的な不連続を示さないことである。様々な不定性を考慮すると、過去の平均星形成率は現在の値に較べ、精々５倍大きいか、３倍小さいかである。我々は変動幅はファクター２程度と考える。星形成史に対する副次的な１２の拘束を与える。星形成率がガス密度の二乗に比例するという証拠はない。もし、星形成率がガス密度のべき乗としても、その指数は 0.5 以下である。

　連続性の拘束に矛盾しない幾つかの星形成史に対して、 IMF を求めた。得られた IMF は滑らかで、 log M に関しハーフガウシャン、つまりログノーマルである。IMF の勾配は dlogξ/dlogM = -(1 + logM) である。現在の質量消費は (3 - 7) 10^-9 Mo pc^-2 yr^-1 である。ガス消費のタイムスケールから、星形成はガスの落下率と釣り合っているか、または星形成率が超新星や銀河衝突によりストカスティックに制御されていることを示す。IMF の形は星団 IMF と大体合っている。

　１．イントロダクション　

　２．現在の質量関数　

　定義　

質量関数　φ_ms(logM)dlogM = dN (stars pc^-2)

光度関数　φ_ms(logM)=φ(Mv)|dMv/dlogM|2H(Mv)f_ms (Mv)

ここに、H = Mv 星のスケール高、f_ms(Mv) = 主系列星の割合。質量関数は円盤上の投影表面密度、光度関数は主系列星も含めた太陽近傍での空間数密度という違いがあることに注意。質量関数、光度関数のどちらも φ を使っていて紛らわしい。

図１．光度関数 φ(Mv)。黒丸＝McCuskey (1966), 白丸＝Luyten (1968), バツ＝Wielen (1974)。実線＝使用する関係。

図２．近傍の主系列光度関数 φ(Mv).黒丸＝実視連星。白丸＝食連星。バツ＝分光連星。破線＝理論。実線＝使用する近似線。 　

　スケール高　

表１．使用した関係量

図３．Mv とスケール高 H の関係。黒丸＝Schmidt 1963, 白丸＝Schmidt 1959, バツ＝Upgren 1963, 三角＝McCuskey 1966. W=Weistrop, B = BokmMacRae 1941, E = Elvius 1951,1962, A = Allen 1973.

表２．f_ms(Mv) = Mv における主系列星の割合。

　

　PDMF = 現在の質量関数　

表３．主系列星の PDMF (stars pc^-2 logM^-1) 　

図４．φ_ms(logM) = 主系列星の PDMF (stars pc^-2 logM^-1) 　

図５．φ_ms(logM) = 主系列星の PDMF (stars pc^-2 logM^-1) 　

表４．PDMF の不定性

　３．太陽近傍の星形成史　

　定義　

C(logM, t)dlogMdt = 円盤単位面積当たり dlogMdt 内に生まれる星数

T_ms = 主系列寿命、To = 銀河系年齢

　　　φ_ms(logM) = ∫_To-Tms^To C(logM,t)dt　　　Tms<To (3)
　　　φ_ms(logM) = ∫₀^To C(logM,t)dt　　　Tms≥To (4)

⟨C⟩ = 単位ログ質量当たりの時間平均星形成率
　　　　　 = ∫₀^ToC(logM,t)dt/To= ξ(logM)/To　　(5)

ξ(logM) = 単位面積、単位ログ質量あたり、今までに生まれた星の総数

B(t) = 絶対総星形成率 = ∫_-∞^∞ C(logM,t)dlogM　　(6)
⟨B⟩ = 絶対時間平均関数 = ∫₀^To B(t)dt/To

　星形成率を質量部分と時間変化部分に分解　
C(logM,t) を次のように、時間部分と質量部分の掛け算と仮定する。
C(logM,t) = ξ(logM)b(t)/To
ここに、相対星形成率 b(t) ＝平均星形成率を単位にした相対星形成率

b(t) は Schmidt 1959 が最初に用いた。すると、(3),(4) は
φ_ms(logM)=(ξ(logM)/To)∫_To-Tms^To b(t)dt　　Tms<To　　　(10)
φ_ms(logM)=(ξ(logM)/To)∫₀^To b(t)dt　　Tms<To　　　(12)
　　　 = ξ(logM)
これは、∫₀^Tob(t)dt = To だからである。

　初期質量関数 IMF　
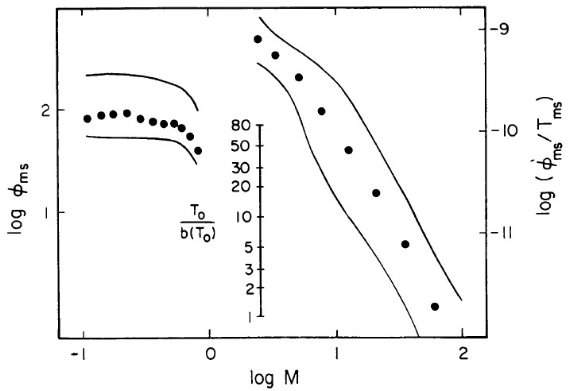
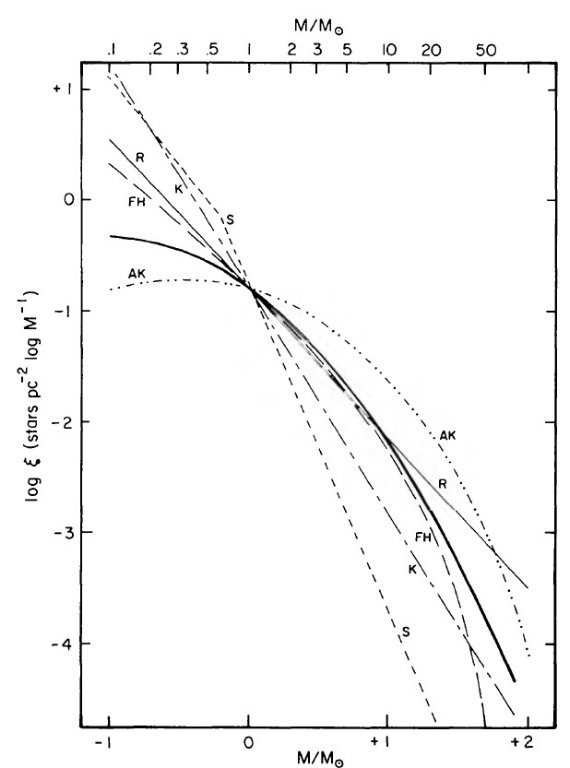
　図７からすぐ分かるが、IMF の大質量星部は星形成史の形に依らない。これらの星の数は現在の星形成率を直接反映し、過去の星形成史と無関係である。

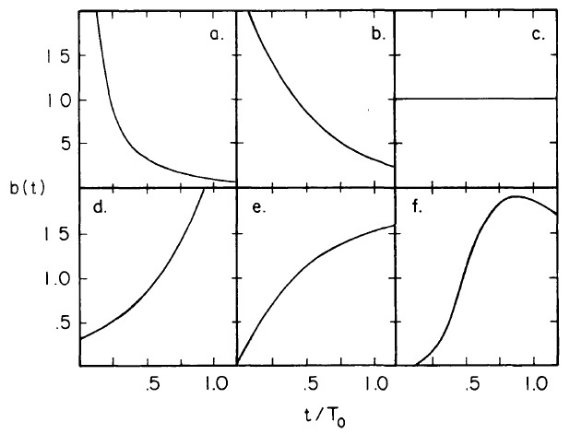
図６．テスト用形成率。(a): Schmidt n=2, (b) 減衰指数関数型, (c) 一定、 (d) 増加指数関数型、(e) 漸近増加型、 (f) 多項式型 　

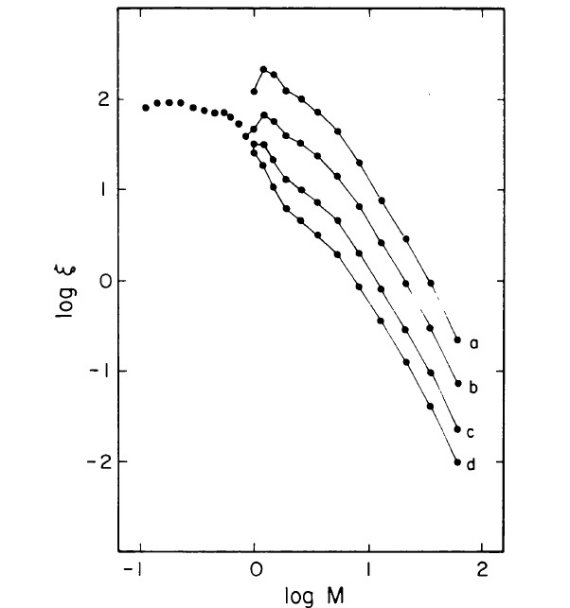
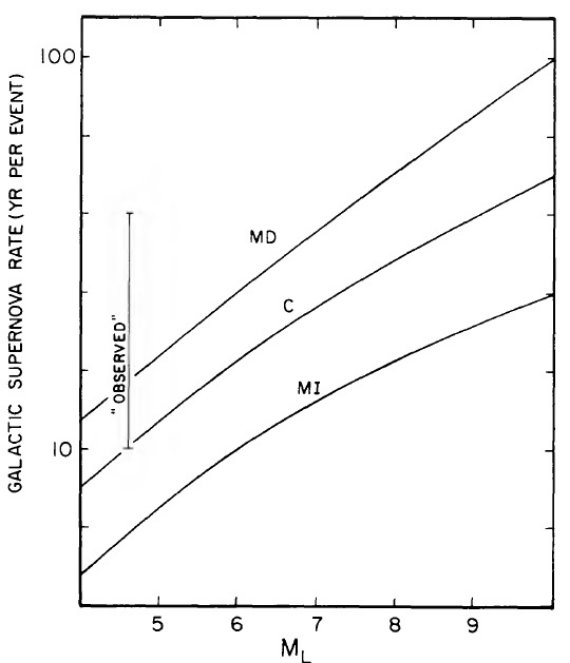
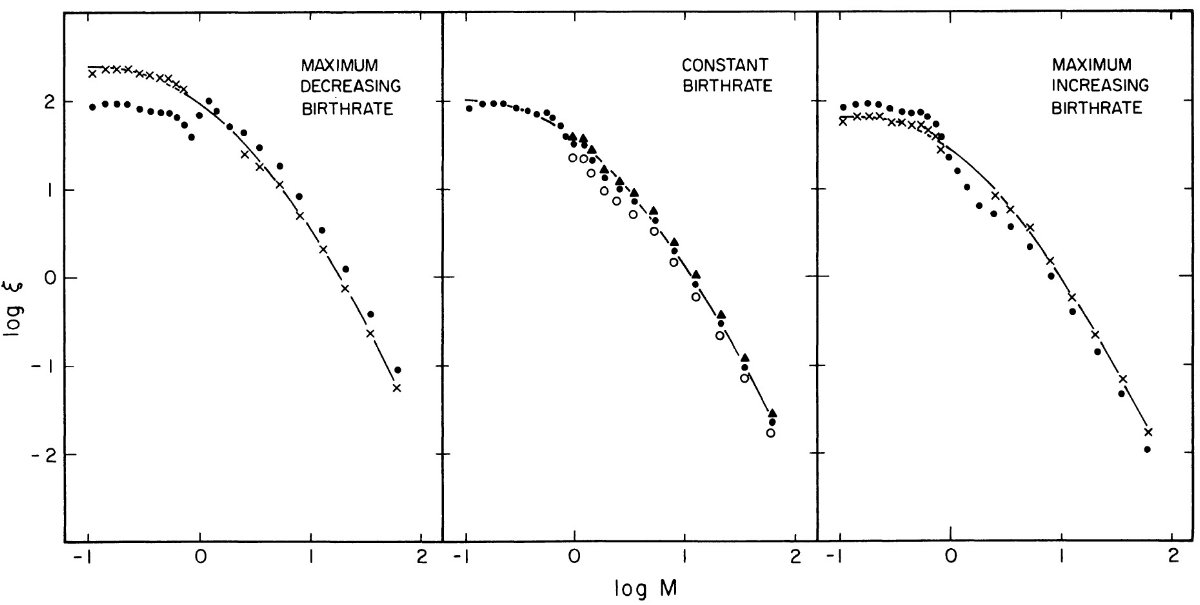
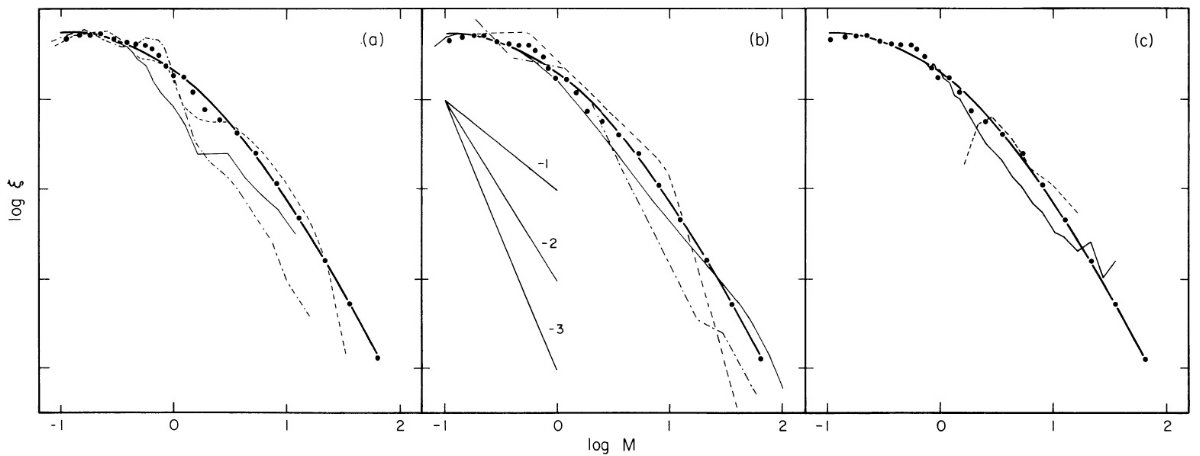
図７．幾つかのテスト b(t) に対する式 (10), (12) から導いた IMF. 漸近増加型と多項式型は曲線 c と d の中間に来るが図示を省いた。

図８．連続性の拘束から導かれる現在の星形成率への制限。左側は Tms > To の星の PDMF φ_ms. これ等の星では IMF = PDMF である。右側は Tms << To の星の PDMF/Tms を示す。これらの星では IMF は (φ_ms/Tms) と (To/b(To)) の積で与えられる。　

　IMF に不連続　

　また、仮定 (b) のように急激に星形成率が下がるモデルでは、主系列星寿命が銀河年齢と等しくなるところで、 IMF に不連続を生じる。これは、そのような星では既に消えた星の補正が非常に大きくなり、過剰補正が生じるためと思われる。

表６．急増、急減星形成率での拘束。 　

表５．現在の相対星形成率 　

図９．超新星発生率と超新星限界質量の関係。 　

図１０．IMF のモデルによる変化。

表７．ＩＭＦへの解析フィットパラメタ―

表８．ＩＭＦの総星数と総質量。

表９．Fn と Fm。

図１１．文献からの IMF の比較。

図１２．様々な分裂過程による質量関数の比較。 　