Giant M Stars in the Galactic Anticenter

　２．観測データ　

観測領域の中心は (RA, Dec)1950 = (6h00m, 24.2°:), (l, b) =(186, +1) で、b = [-1, +3] をカバーする 8 deg2 である。 McCuskey 1967 はもっと広い、 18.55 deg2 で OB-星と V = 12.5 等より明るい B5 - M8 星の分布を調べた。この論文ではそれより狭い領域で 暗い M-型巨星の分布を調べる。 　２．Ａ．スペクトル　 　フィルター 　分類に用いたスペクトルは Warner-Swasey Obs. Burrell Schmidt 望遠鏡 に 1-N 乾板/Wratten W89 フィルターの組み合わせで得た、 λ6800 - λ8800 A のものである。A-バンドでの分散は 1700A/mm である。 これは M5 より晩期用。103-F/OG2 で λ5900 - λ6900 を もっと早期用に撮った。限界等級は M2 - M4 で V = 15, M5 より晩期で V = 16 である。 　分類基準　 　Ｍ型星のスペクトル分類基準は Nassau, van Albada 1949, Cameron, Nassau 1955, Nassau, Velghe 1964 に述べられている。今回は Nassau, Velghe 1964 の Burrell Schmidt スペクトルをしばしば参照スペクトルとして使用したので、分類は Nassau, Velghe の Case システムに則る事になった。Mt. Wilson 分類システムへの変換は Blanco 1964 に従って行った。一般には エラーは ± 0.5 サブクラスである。 光度クラスはこの分解能では定まらない。しかし、Blanco 1963 は この程度の広がりと深さでは 矮星、準巨星、超巨星の M-型星は 殆ど含まれないことを示した。従って、今回は全てを巨星として 扱う。 　２．Ｂ．測光　 　ショットの GG11 フィルターが V 測光に用いられた。そして、 8 deg2 観測領域内の V = 16.5 より明るい 493 M-型星と 16 炭素星の V 等級を測った。 内部エラーは 0.05 等級である。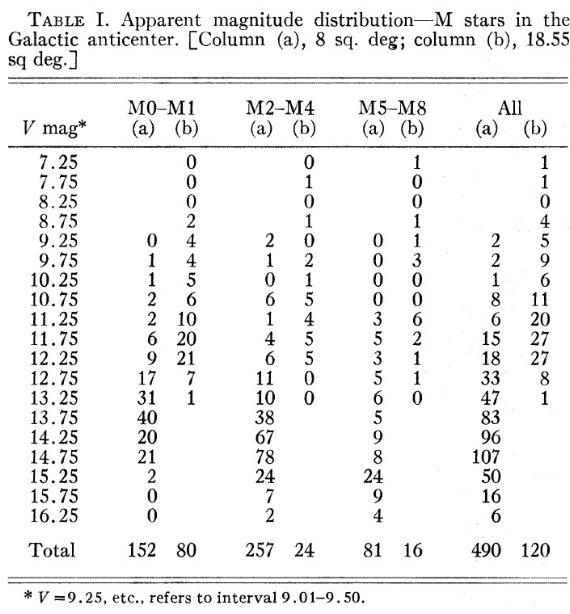

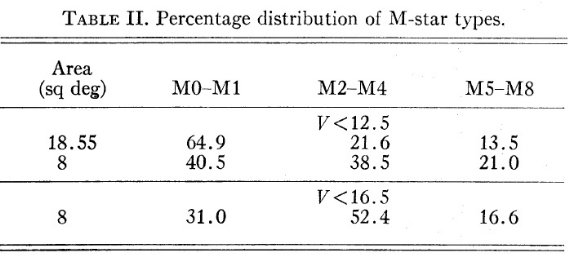
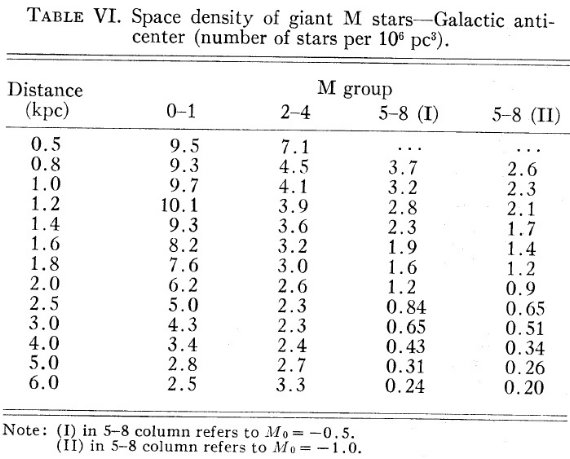
表１．反中心方向 M 型星の見かけ等級分布。(a) は 8 deg2 領域、 (b) は 18.55 deg2 領域を指す。

　３．データ解析　

表２．M-型星のサブグループ分布 　M-型星の分類　 　表１には銀河系反中心方向 8 deg2 と 18.55 deg2 領域での M-型星の等級分布を示す。光度クラス Ia と Ib の４星は大領域から、 ３つの特異星を小領域から除いた。M-型星は M0 - M1, M2 - M4, M5 - M8 の ３集団に分けて数えた。 Blanco 1965 は低分散スペクトルで M0 と M1 への サブ分類は難しいことを指摘した。しかし、スペクトルを広げ、103a-F を使用 することによりこの問題は改善されたので、M0 - M1 グループを統計に加えた。 しかし、解析の主力は M2 - M4, M5 - M8 グループを対象としている。 　中間グループ星数の揺らぎ　 　表２は 8 deg2 と 18.55 deg2 領域とで 相対的等級分布を比べた。晩期 M-型星の比率は変わらないが、早期 M-型星の比率は異なる。Vlimit が上がると M2 - M4 グループが 増える原因の一部は低分散では M0 - M1 グループに分類することが難しい ためかも知れない。しかし、表１に見られるように　Vlimit = 12.5 にして分類エラーを下げても M0 - M1 グループと M2 - M4 グループ の相対比の差は依然存在した。したがって、 M-型星種族の揺らぎが実際に この差に反映しているのであろう。 ( 揺らぎでなく、例えば b-勾配 が反映したのかも知れない。)

表３．他の反中心方向探査との比較 　他の探査との比較　 　表３では、 M2 - M4 星と M5 - M10 星の平方度当たりの数を様々な 探査で比較した。Sanduleak 1957 は低減光の小領域に限定した探査であり、 星密度が高いのはその結果である。しかし、それ以外の探査でも星数の 揺らぎは存在しているらしい。

表４．M-型星グループ毎の log A'(V)。 A'(V) = [V-1/4, V+1/4] 区間内の 星数/100 deg2. 　見かけ等級関数の平滑化表示　 　表１の星数計数は A'(V) = ΔV 0.5 等区間内にある 100 平方度当たり の星数、に変換された。log A'(V) を V に対してプロットし、それを平滑化 したものを表４に示す。 　平均絶対等級　 　表５には星の空間数密度を計算するために用いた平均絶対等級 (単位体積当たりとあるのが意味不明？)とその分散を載せた。値は Blanco 1965 とそれに Malmquist 1927 バイアス補正をしたもの である。 　星間減光 Av　 　Av の距離による変化は McCuskey 1967 から採った。Av(1kpc) = 1 mag, Av(5kpc) = 2.4 mag である。 　空間密度　 　空間密度は Schwarzschild 1912 の解析的方法で求めた。この手法は Crowder 1959 によって採用されたものである。表６にその結果を示す。表の最後の ２列は使用する絶対等級を 0.5 等変えるとどう変わるかを示している。 　直接計算した密度と較べる　 　M5 より晩期の星の数は少ないので密度の決定精度は低い。数の小ささが どのくらい影響するかを見るため、個々の星の距離を決定して、密度を 直接に決めてみた。各星に Mv = -1 という絶対等級を与え、 McCuskey 1967 が決めた星間減光を適用して距離指数を計算した。こうして 81 星 を適当な距離区間に分布させ、密度を計算した。図１がそれである。 0.5 kpc おきに 8 deg2 と 18.55 deg2 に対して 密度変化が得られた。実線曲線は計算機で得た密度変化である。 両者の一致は大変に良い。

表５．平均絶対等級と分散 表６．銀河系反中心方向での空間密度分布(星/106pc3) 図１．M5 - M8 星の数密度変化。実線＝モデル。丸、バツ＝個々星の距離 計算に基づく観測値。

図２．M0 - M1 星の空間密度変化。曲線 A は Blanco 1965 の表。

図３．M0 - M1 星の空間密度変化。データ点と実線＝この論文。 破線 A ＝ Hidajat, Blanco 1968. B = Blanco 1965.C = Neckel-Blanco 1965。D = Westerlund (1965). E = Wehinger 1965.

　４．討議　

　４．Ａ．早期 M-型星　

　４．Ｂ．晩期 M-型星　

M5 - M8 巨星数密度　 　図４には、 M5 - M8 巨星数密度の反中心方向距離依存を示す。 図中には他研究で得られた値もプロットした。大部分はシグナスー カリーナ局所腕方向に対する値である。 (それだと銀河中心距離では変わら ないが？ ) 図から明らかなのは、r = [1, 4] kpc の間に急激な密度低下が起きている ことである。注意しておくが、 r = [1, 2] kpc での高い密度はサンプル数 を考慮すると不確実である。類似の密度の負勾配が M2 - M4 星密度 でも観察されている。N(M2-M4)/N(M5-M8) = 2(r=1kpc) - 7(r=4kpc) である。 Westerlund 1965 は渦状腕でこの比が 10 -1 と述べている。 　r > 4 kpc では　 　Westerlund 1965 によれば、 局所腕に沿っては M5 - M8 星の空間密度が　 r > 4 kpc でほぼ一定である。その値は D(r) = 0.2 - 0.3 星/106pc3 であった。反中心方向に関しては 遠距離で密度増加の兆候はない。 　銀河系中心方向　 　Wehinger 1965 は、銀河系中心方向　r = [2, 5] kpc で、D(r) = 1.1 星/106pc3 (図４ B) とした。つまり、晩期 M 型星 の r = [3, 5] kpc での密度は、銀河中心方向では反中心方向の 2 - 4 倍大きいということである。 　密度勾配　 　Hidajat, Blanco 1968 は M5≥ 星の反中心方向空間密度を 次の式で表した。 　　　　　D(r,z) = [202/(R2+102)]exp(-5.1z2) ここに、(R,z) は銀河中心からみた円筒座標系(単位 kpc)である。 Ro = 10 kpc とした。表７の数字はこの式から計算した。 "Obs" 列は表６から採った。 明らかに反中心方向での密度勾配はこの式で計算されるより急である。 r < 2 kpc では上の式は Wehinger のデータ(図４B) と一致する。 もし、D(r=1kpc) = 2.3 という我々のデータを無視すれば、我々のデータも 合うと言ってよい。

図４．M5 - M8 星空間密度の反中心方向距離変化。実線＝この研究。 A = Hidajat-Blanco 1968. B = Wehinger 1965. C = Neckel,Blanco 1965, 他の点 = Westerlund 1965. 表７．Hidajat-Blanco 1968 との比較。