アブストラクト光度関数の導出南銀極方向 18.24 deg2, I = 18 mag. より明るい星 12,500 個の 絶対等級を測光視差から求めた。それらから、太陽近傍星に対する絶対可視等級、 絶対輻射等級の光度関数と質量を導いた。 太陽近傍での星質量密度は 0.083 Mo pc-3, 質量光度比は 1.2 (Mo/Lv,o) である。 密度の高度変化 我々はまた銀河面からの高さに応じた密度変化を、各絶対等級毎に求めた。 光度関数は高さにより規則的に変化する。 Mv < +4 の星は暗い星に比べ 銀河面への集中度が著しい。Mv ≥ +4 の星の密度則は、 100 ≤ z ≤ 1000 pc ではスケール高 300 pc の指数関数則、1000 pc ≤ z ≤ 5000 pc ではスケール高 1450 pc の指数関数則に従う。この第2のグループ星は太陽近傍で 2 % を占める。 「厚い円盤」 スケール高 300 pc 成分は古い円盤であり、1350 pc 成分は「厚い円盤」と考える。 「厚い円盤」の光度関数と密度則は楕円体等密度面が銀河系円盤の重力で平坦化した と考えられる。 |
1.イントロ測光視差でミッシングマスを探す論文I(Reid 1982)では対物プリズムで決めた低光度矮星にカラー光度関係を適用して、 光度関数を決めた。その結果求めた太陽近傍密度は運動学的手法から決めた 密度とよく一致した。ミッシングマスを説明できるほどの低光度、低速度分散 の主系列星グループの証拠は見つからなかった。ただし、このサンプルは ただし、 +7 ≤ Mv ≤ +12 で、太陽から 50 pc 以内の領域に限られている。 もっと暗い星にもなかった 論文 II (Reid, Gilmore 1982)では、 I = 17.0 までの自動測光により、 Mv = +19 まで伸ばした。やはり、測光による光度関数は運動学による光度関数と 一致した。これで星の質量領域にはミッシングマスはないと結論される。 「厚い円盤」 この論文では 太陽から 100 pc 内に位置する 12500 星の絶対等級を求める。 そして、光度関数の変化、数密度勾配を銀河面から 5 kpc まで求める。その結果 「厚い円盤」の存在を導いた。 |
2.1.写真観測観測とデータ整約観測の詳細は Reid, Gilmore 1982 に述べられているのでここでは簡単な紹介をする。 我々の主データは UK シュミットで撮った V (IIaD + GG495) 3 枚と、 I(IVN + RG715) 3 枚の乾板である。中心位置は RA 00h53m, Dec -28°03' で SGP に 非常に近い。乾板の測定は COSMOS で行った。等級較正には 250 光電測光標準星と、 1500 写真測光標準星が使われた。 絶対等級ーカラー関係 この観測で得た測光結果と誤差 10 % 以下の三角視差の両方が揃った 202 星に 対して, 絶対等級ーカラー関係を導いた。視差エラーによる絶対等級への Lutz-Kelker 補正も行った。 12,500 星サンプル Reid, Gilmore 1982 では小質量星の光度関数を調べた。そのため、我々は I ≤ 17.0, V - I ≥ 2.4 (Mv ≥ 14.5) の完全サンプルを作り、それらの JHK 測光を実施した。そこにも述べたが、 Pickering プリズム乾板から得た 二次標準星を使い、V ≤ 19.0, I ≤ 18.0 の完全サンプル 12,500 星を作った。 それらの V - I カラーも同時に得た。赤化のない近傍主系列星には Mv - (V-I) 関係が成立する。 2.2.空間密度メタル量勾配低メタル星が系統的に光度が下がることは良く知られている。従ってもしも平均 メタル量と他の量、例えば高度、との間に相関があると、系統誤差が生じる。 ∂[Fe/H]/∂z = -0.225/kpc (Janes 1979), から -0.8/kpc (McClure, Crawford 1971, Jennens 1975, Joss,Hartkopf 1979) まで散らばるが、 -0.30/kpc が最近の典型的な値である。しかし、状況が混乱しているので、二つの式を考えた。 |
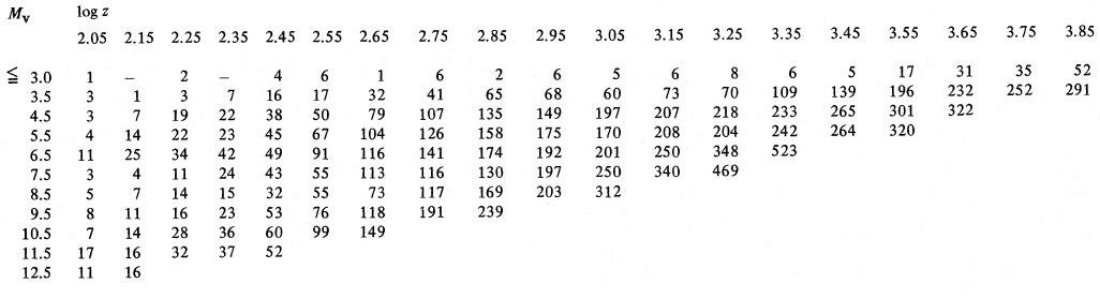
である。第2の場合 5 kpc < z では, [Fe/H] = -1.5 である。 次にメタル量が絶対等級に及ぼす影響が必要となる。Hansen 1979 が準矮星から ΔMv = 太陽メタル主系列から何等下がるか、δ(U-B)0.6 = B - V = 0.6 で規格化された紫外超過、とした時、導いた関係は ΔMv = -0.35 + 5.41 δ(U-B)0.6 この関係式を Carney 1979 の δ(U-B)0.6 と [Fe/H] との関係を 結び付けるのだが、この関係式は非線形である。しかし、最終的には ΔMv = 0.23 z 0 ≤ z ≤ 2 kpc = 0.46 + 0.13(z - 2) 2 ≤ z ≤ 5 kpc = 0.85 5 kpc ≤ z Mv - カラー関係から導いた Mv は上の補正式を適用される。実際には補正なしで 距離を求め、補正して新しい距離を求めという繰り返しが収束するまで行う。 赤化 SGP 方向では Av < 0.1 であり、無視できる大きさなので, Av = 0 と仮定する。 距離と密度 こうしてメタル量勾配、赤化を考慮して絶対等級から個々の星までの距離が求まる。 マルムキストバイアスも考え、与えられた絶対等級と距離に対する数密度が直接 求められる。表1と表2には上で決めた二通りのメタル量勾配に対する数密度が 表で与えられている。表の行に沿っては光度関数が、列に沿っては密度則が読み取れる。 |

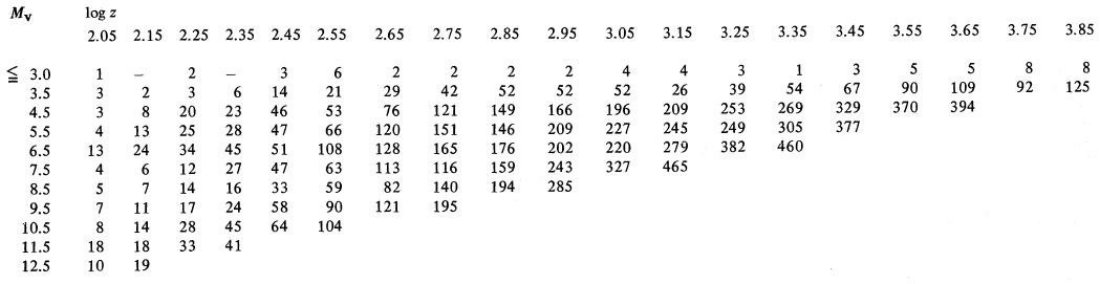
3.1.太陽近傍の光度関数3.1.1.銀河面への補正100 pc 以内の星の完全サンプルに基づく主系列光度関数論文II では 100 pc 以内の星の完全サンプルに基づき、9 ≤ Mv ≤ 19 の主系列光度関数を導いた。4.2. 節ではこれを z = 0 での関数に戻す方法を 研究する。 それらの結果から、3 ≤ Mv ≤ 11 の主系列星は z = 100 pc から z = 1000 pc の間でスケール高 300 pc の指数関数則に従うことが判っている。これは、 メタル変化の様子に関係なく成立する。この規則が z = 0 まで、また Mv = +19 まで 伸ばせるなら、z = 0 での光度関数は容易に求まる。しかしながら、非常に低質量 の星までこの規則に従っているかどうか疑わしい。 絶対等級でスケール高が変化しないか? Mv ≥ +11 の暗い星でも明るい星と同じスケール高を有しているという仮定は、 この等級より明るい方でも暗い方でも初期質量関数が銀河系円盤の年齢程度の時間 では変化しないことを意味する。これは物理的に尤もらしい。 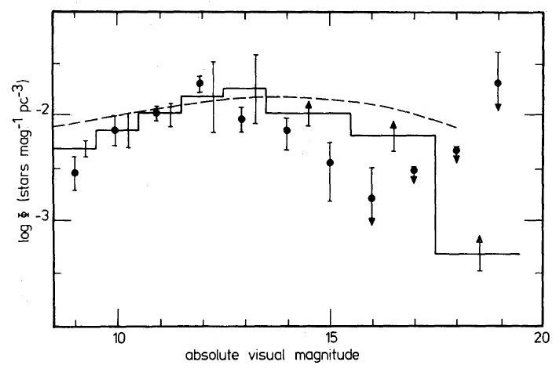 図1.黒丸=テキストの方法で修正した z=0 光度関数。実線 = Wielen 1974, 破線 = Luyten 1968 光度関数 |
z = 0 での光度関数 指数関数を z = 0 まで延長して良いかどうかは疑問の余地がある。4.1.節で 論じるが、Mv ≤ +3 の星はスケール高 100 pc で普通「若い円盤」と呼ばれている ことを知っている。この密度則は光度関数にも反映されるべきであるといって面倒 くさい議論が展開されるが略。修正された光度関数はWielen 1974, Luyten 1968 光度関数と共に表3、図1に示した。関数の不確実性は主系列星の不確実性である。 この論文は意味の取りにくい記述が多い。 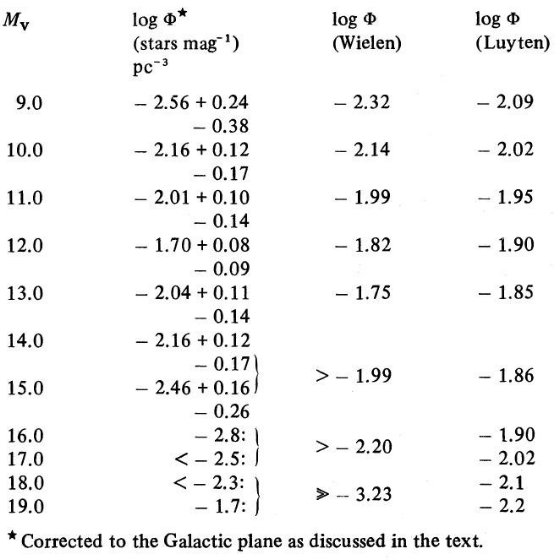 表3.銀河面での光度関数 |
3.1.2.輻射等級光度関数輻射補正Mv ≤ +9 の星に対する輻射補正は Allen 1973 から得られる。より暗い星に 対しては Veeder 1974, Greenstein, Neugebauer, Becklin 1970 から得た。その結果を 図2a に示す。 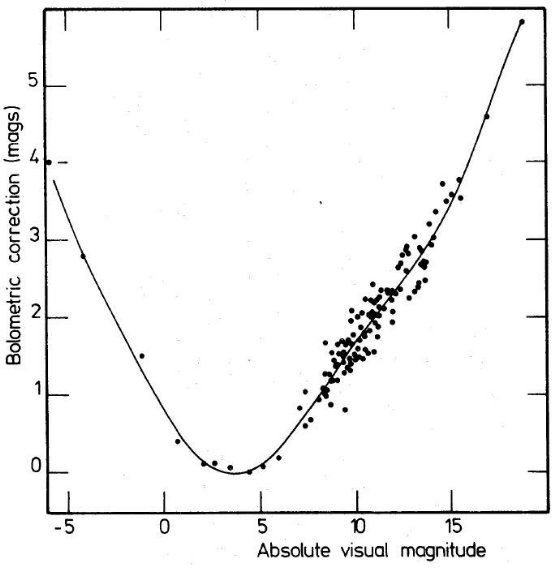 図2a. 輻射補正と絶対等級の関係 |
輻射等級光度関数 輻射等級光度関数を得るために、-6 ≤ Mv < +2 ではMiller,Scalo の可視等級 光度関数を用い、+2 ≤ Mv ≤ +10 では Wielen の表、+10 < Mv には 3.1.1.節の結果を用いた。最終結果は表 4(a) に載っている。 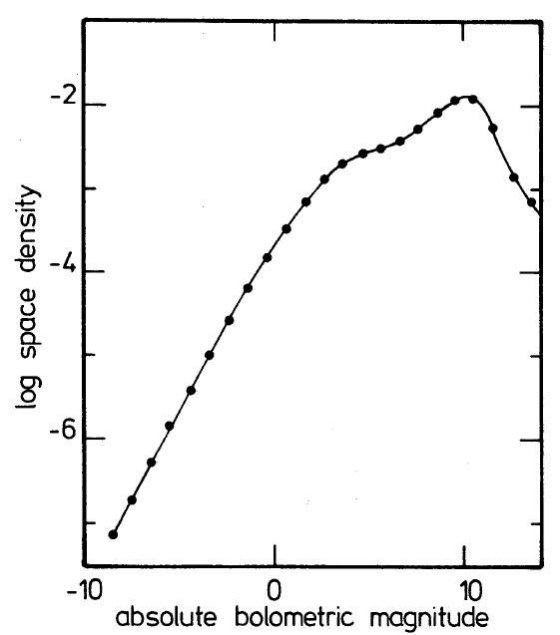 図2b. 輻射絶対等級の分布(光度関数) |
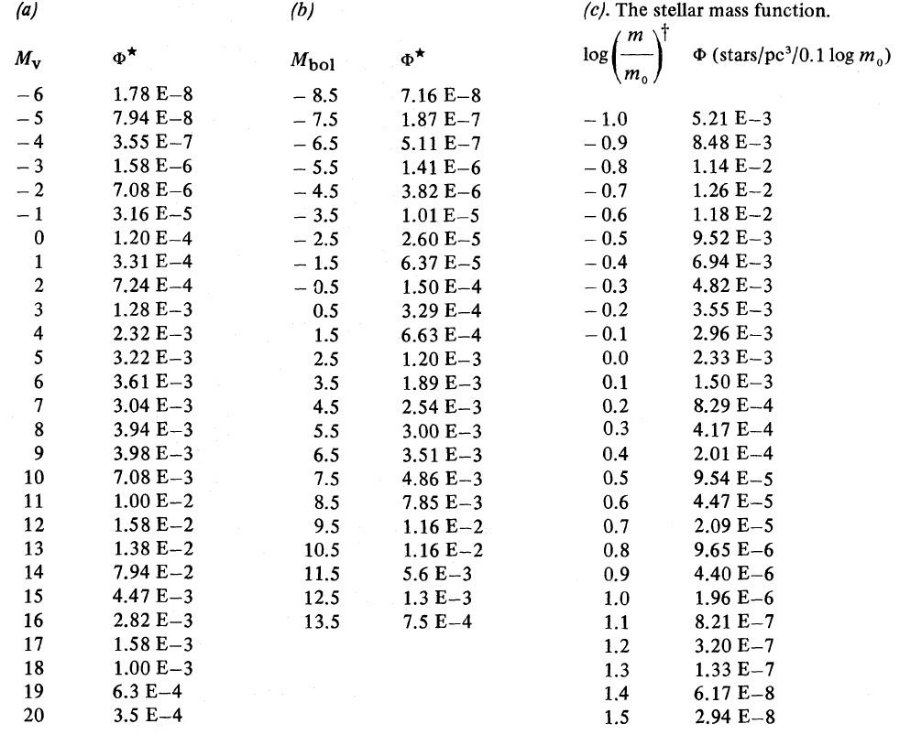
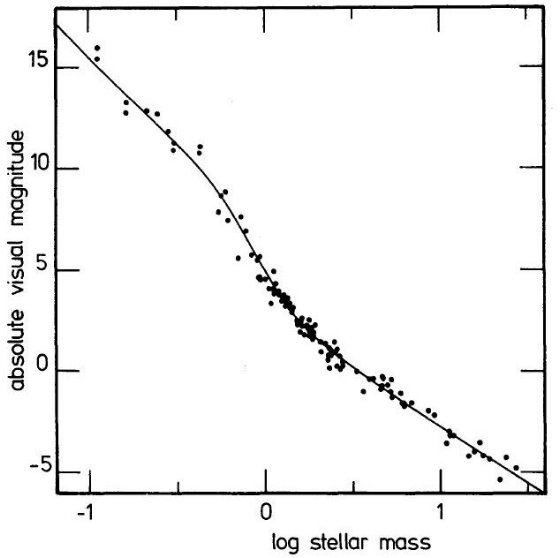 図3a. Popper 1980 の質量光度関係 質量光度関係 主系列星の質量光度関係は Popper 1980 がまとめていて、図 3a に示した。 これを表 4a の光度関数と組み合わせて質量関数が得られる。 |
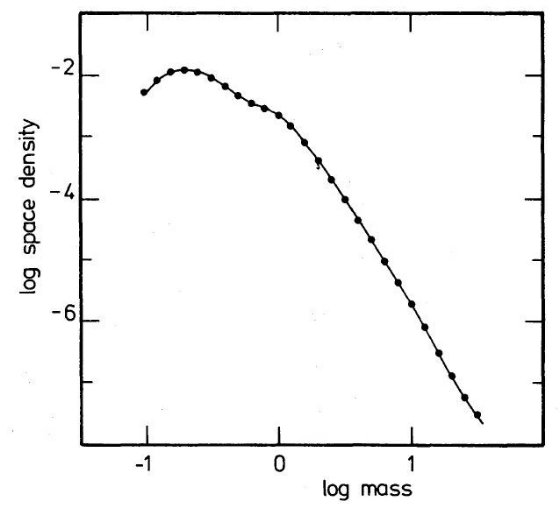 図3b. 質量関数 質量密度 この関数を積分すると、-1 ≤ log(M/Mo) ≤ 1.5 範囲での、太陽近傍での 質量密度が得られる。その値は 0.038 Mo pc-3 である。 |
|
光度関数の高度変化 高度が上がると Mv ≤ +3 の星が減ってくるため、光度関数が変化して行く 事は以前から知られていた。しかし、これまでは十分に深いデータによる研究は なかった。今回得られた光度関数は高度変化を良く示している。図4(a) と (b) に二種類のメタル量変化の仮定に応じた光度関数変化が示されている。 図の著しい特徴は Mv ≤ +4 での光度関数が高度と共に系統的に 急落して行くことである。この急落は表5にはっきり示されている。表には Mv ≤ +3 の相対的な星の割合が減少していることがはっきり示されている。 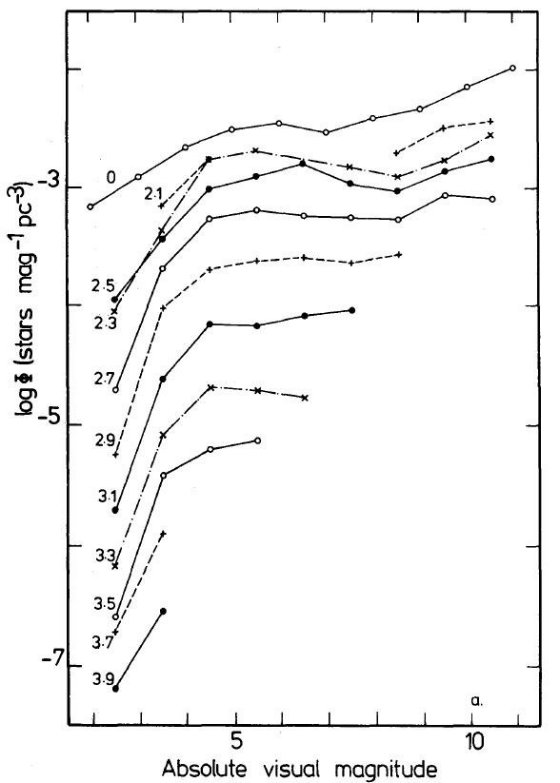 図 4 a. 光度関数の高度変化。メタル勾配なし。 |
 表5.絶対等級での数比 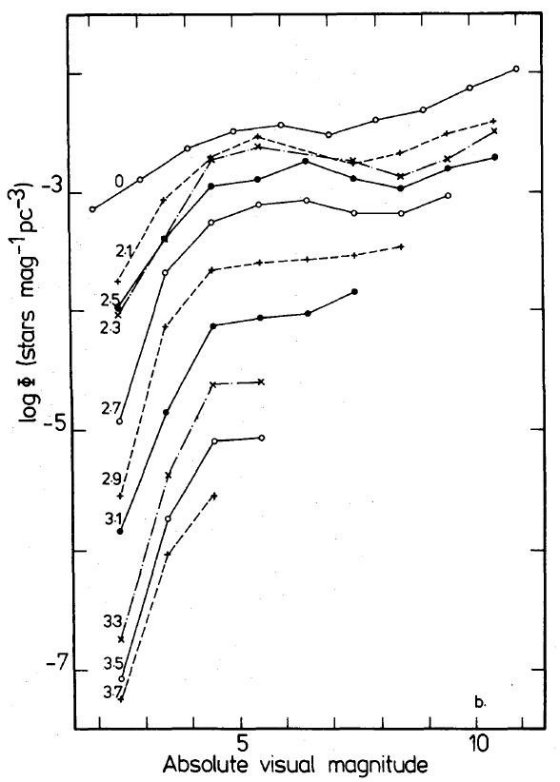 図 4 b. 光度関数の高度変化。メタル勾配あり。 |
4.1.証拠A - F 矮星の密度則Hill, Hilditch, Barnes 1979 は A - F 矮星の密度則を北銀極方向で定めた。 その結果は指数関数には良くフィットしない。しかし、無理に合わせると、F 型星は z = 500 pc まではスケール高 125 pc で、A 型星はたった z = 300 pc までしか合 わせられずスケール高 90 pc である。そこより高くなると、A 型星の状況はより はっきりしなくなる。Woolley, Stewart 1967 は A 型星の解析から z = 300 pc まで スケール高 90 pc で良く合うとした。その上は z = 500 pcまでは スケール高 150 pc が合う。 |
Mv ≤ +8 Eriksson 1978 は南銀極方向の Mv ≤ +8 の巨星と矮星に対する密度則を 導いた。彼によると、z < 1 kpc, z = 1 - 3 kpc、3 kpc < z でそれぞれ 異なるスケール高を必要とする。この結果は Bok, Basinki 1964, 本論文と一致する。 暗い星 暗い星 Mv > +5 に対しては Faber et al 1976, Sandage,Katem 1977, Chiu 1980 の解析がある。Faber et al 1976 によると、 Mv = +17 でスケール高 300 pc である。 Sandage, Katem 1977 は M15 領域での M 矮星 +8 ≤ Mv ≤ +12 のスケール高を 470 pc とした。かれらは z = 2 kpc までは円盤星が楕円体星より多いとコメント した。Chiu は暗い固有運動星の解析から +4 ≤ Mv ≤ +13 に対し、スケール高 300 - 500 pc を得た。 |
表2を使い、スケール高を定める。その際、V > 18.5、V ≤ 14 の
K 型星、100 pc ≤ z ≤ 1000 pc の外のデータは捨てる。これらの
前準備は銀河の混入、GK 矮星への遠い巨星の混入を最小化し、単一指数関数則
が妥当する範囲に限定するために必要である。表5に我々の結果を示した。Mv >
+3 の平均はメタル勾配なしで 302 pc, ありで 303 pc である。これは古い円盤の
スケール高に合っている。
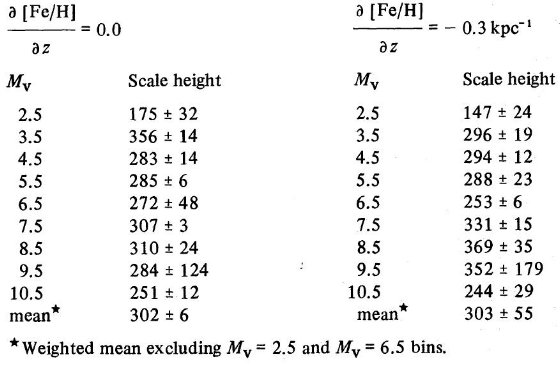 表6.円盤スケール高 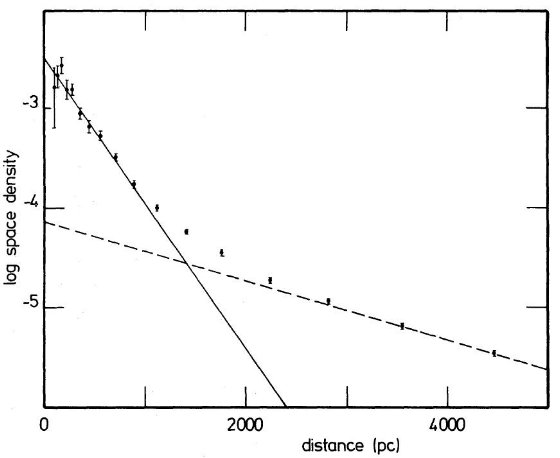 図 6 a. 4 ≤ Mv ≤ 5 星の質量密度の高度変化。フィット直線はスケール高 300 pc と 1350 pc. |
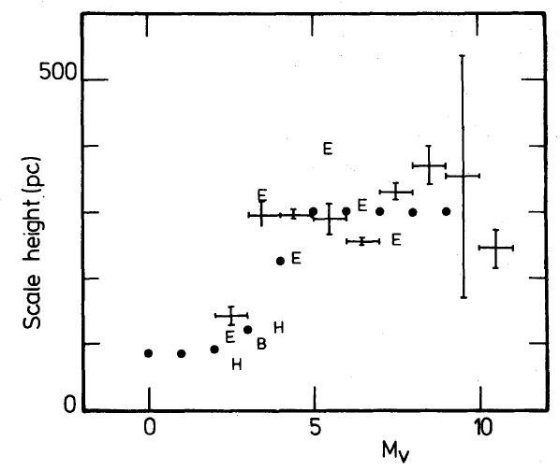 図 5 . 100 pc < z < 1000 pc での絶対等級による円盤スケール高の変化。 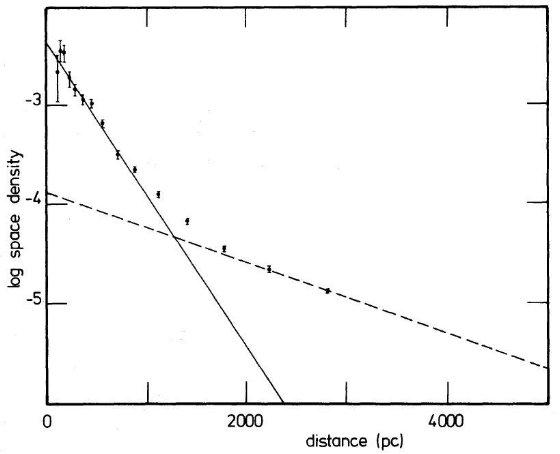 図 6 b. 5 ≤ Mv ≤ 6 星の質量密度の高度変化。 |
5.1.現在の標準モデルの証拠5.1.1.球状星団球状星団の分布は ρ(r) ∝ r-3.26±0.23 で 表わされる。5.1.2.RR LyrKinman et al 1966 は ρ(r) ∝ r-3.4±0.23、 Oort, Plaut 1975 は ρ(r) ∝ r-3.0±0.23で 表わされるとした。5.1.3.フィールド星Weistrop 1972Weistrop 1972 は北銀極付近 13.5 deg2 14000 星の UBV 観測 を行った。彼女のデータは精度が低いが、 M 92 光度関数を使った∼r -3 モデルとは合致する。ただ、精度の点で重みは低い。 |
Chiu 1980 Chiu 1980 は 0.3 deg2 で V = 20.5 までのデータを用いた。 星数が少ない。 Becker 1980, Fenkart 1980 Basle グループの 10 deg2 RGU 写真測光を用いた。ただ、初めから 種族IIを仮定している。 ようするに、 今までの結果は 1 kpc の先の密度則を一意に決定できなかった。現在ある データはスケール高 ∼ 4±2 kpc の円盤でも、指数則の 球でも合う。 |
|
べき乗型密度則 図7は図6と同じデータだがスケールを log - log にしてある。1 kpc より内側は データはスケール高 300 pc の指数関数型で良く合う。その先は2種類のフィット が同じくらい良く合う。一つはスケール高 1450 pc の指数関数、もう一つは
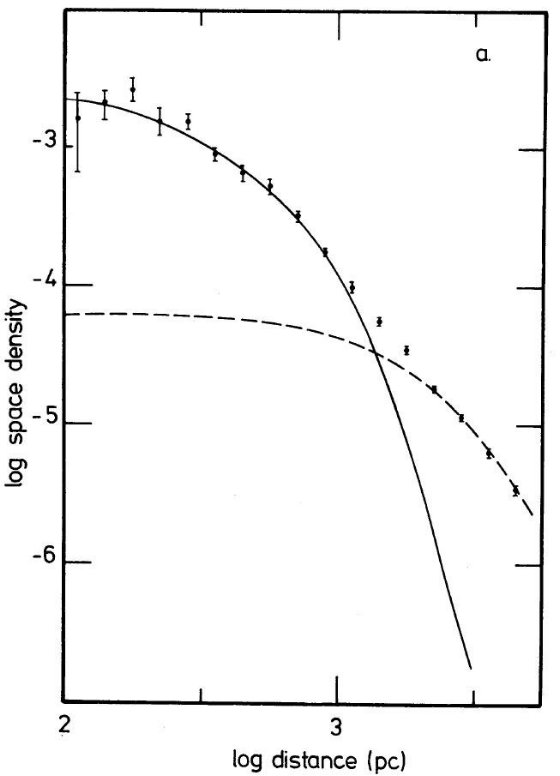 図 7a. 4 ≤ Mv ≤ 5 星の質量密度の高度変化。横軸を log スケールに変換。 実線は指数型フィット。破線はべき乗モデル。 |
Mv ≤ +4 の明るい星 しかしながら、Mv ≤ +4 の明るい星では、z > 1200 pc において、スケ ール高 1650 pc の指数関数か、べき乗則で K = 2 の方が 暗い星でのスケール高 1450 pc 指数関数や K = 4 のべき乗よりよくフィットする。 結論 結論としては、Mv = +4 での光度関数の折れ曲がりより暗い星の z = 1000 pc より遠くでは、スケール高 1450 pc の指数関数型か、指数 = -3.5 で 扁平度 a/c = 4 のべき乗型がよくフィットする。それより明るい星はスケール高 1650 pc 指数関数か、扁平度 a/c = 2 のべき乗でフィットする。どの場合でも 規格化は 2 - 3 % である。メタル勾配の影響は小さい。 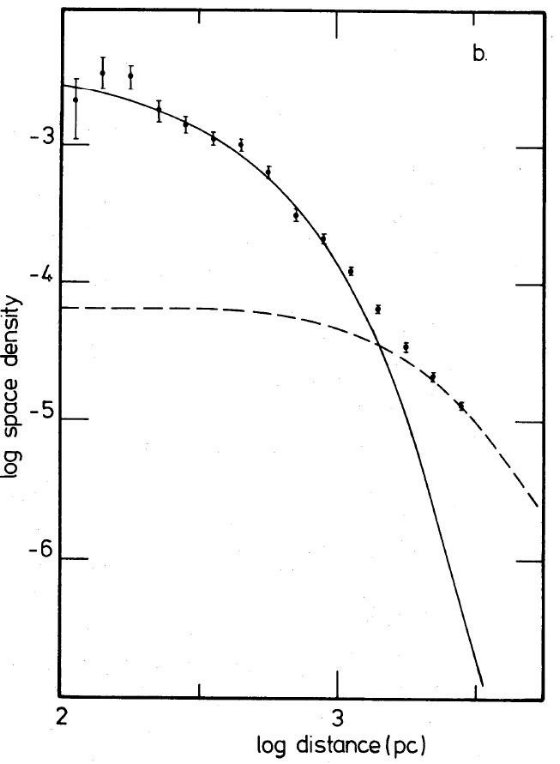 図 7b. 5 ≤ Mv ≤ 6 星の質量密度の高度変化。横軸を log スケールに変換。 実線は指数型フィット。破線はべき乗モデル。 |
6.1.質量関数最近、星の質量関数に二つの重要な特徴が発見された。(1)太陽から 300 pc 以内 M ≤ 1 Mo で勾配が変化する。Upgren, Armandroff 1981 (2)M ≤ 0.2 Mo で質量関数は平坦になる。 これらの特徴は、全ての星質量に単一の物理過程が働くという星形成モデルとは合致 しない。むしろ、低質量星の形成と大質量星形成とは異なる物理過程が働くという説 を支持する。 どういう理屈か? 6.2.B&S 銀河モデルとの比較B&S モデルと SGP データとの比較Bahcall. Soneira 1980b は銀河系のモデルを提案した。それは主に高銀緯での 20 ≤ B ≤ 22.5, B ≤ 16 データと比較された。それらのデータの幾つかは不確実性が大きい ので、ここで提出したデータとの比較は意味があるだろう。図8を見ると 明らかなように、データとモデルとの不一致は大きい。 Tritton, Morton 1982 も別の領域で同じ結論に達している。 不一致の理由 不一致は Mv ≤ +3 で大きいが、その主な理由は楕円体光度関数の形である。 彼らは若い円盤の光度関数を楕円体成分に使用していて、Mv = +4 から明るい方 での急激な低下を考慮していない。第3章で示したように、高度が上がるに連れて、 光度関数の勾配は急になる。これが彼らの採用した光度関数の限界を決めている。 楕円体星で Mv = 0 の星が V = 17 に寄与するのは銀河面から 40 kpc 離れた 所である。そのような遠方でその明るさの主系列星は観測されていない。図8の モデルに現れた青いピークは単に若い円盤と楕円体円盤との光度関数の差を 無視した誤りの産物である。 密度則の誤り B&S モデルの円盤スケール高はこの論文とよく合っているが、z > 1kpc では 我々が導いた密度プロファイルと一致しない。特に 1 kpc < z < 5 kpc では我々は指数関数型か扁平度の大きなべき乗型の密度則を見出したが、B&S モデル は球形の楕円体成分を仮定している。 | 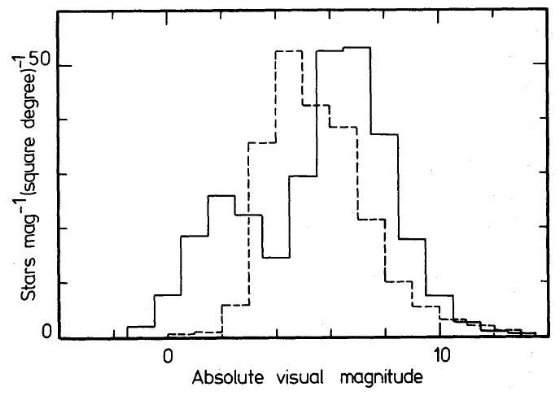 図8.破線=南銀極方向、見かけ等級 15 ≤ V ≤ 17 の星の絶対等級 分布。実線= B&S モデルの予想。 双峰性の原因 不完全な密度分布と不適当な楕円体光度関数の採用により、南銀極方向の 恒星分布データとモデルの予言との大きな不一致に導いた。図8に現れた 絶対等級分布は、しかし、Kron 1980, BS モデルの B > 20 での 星数ー 等級ーカラー分布の双峰性がもっと明るい等級では現れないことを意味しない。 実際、我々のデータも V > 16.5 で双峰性を示している。しかし、これは 絶対等級とカラーの関係の形のせいであり、等級分布の双峰性ではない。 |
|
極端種族 II は却下 極端種族 II の星の数は太陽近傍で円盤星に対して、 1.25 × 10-3 Schmidt 1975, (1±7) × 10-3 Harris 1976, (5±2) × 10-3 Fenkart 1980, 5 × 10-3 Chiu 1980 である。所が我々が 1 kpc < z < 5 kpc で見出した密度則を z = 0 に外挿すると 20 × 10-3 となる。従って「厚い円盤」は極端種族 II ではない。 中間種族 II しかし、中間種族 II なら可能性がある。Stromgren 1964, 1976, Crawford, Mavridis, Stromgren 1979 は測光メタル量パラメター, 0.045 ≤ δM1 ≤ 0.090, と中間的運動学特性を持つことに基づき、太陽近傍 F 型星 の 7 % が中間種族 II であるとした。中間種族 II 星は古い円盤種族の低メタル量 側の端の星とここで論じている「厚い円盤」星の和かもしれない。 中間種族 II を支持する証拠 光度関数の勾配が急になることとこの種族が多分やや低メタルであることは 古い円盤種族よりさらに古いことを意味する。したがって、中間種族 II を 銀河楕円体の太陽近傍成分でその運動学特性が円盤重力ですこし歪められていると 看做せる。最近、幾つかの横向き銀河で空間およびカラー分布が銀河系中間種族 II と矛盾しない成分が発見されたこともこの解釈を支持する。 |
速度分散からの推定 等温自己重力平面系の分布は ρ(z) = ρ(z=0) sech2P(z/z0) で、この式は z が z0 より大きい所ではスケール高 z0/2P の指数関数則となる。ここに P は円盤と考えている種族の 平均二乗速度分散の比である。我々が測ったスケール高は 1450 pc である。円盤の 速度分散を 20 km/s とすると、上式から中間種族 II の速度分散が 60 km/s で あることを意味する。Hartkopf 1981 が得た z 速度分散が 20 km/s([Fe/H]=0.0), 50 km/s([Fe/H]=-1.0)という結果はこれと合致する。Oort 1965 は[Fe/H] ≥ -1 の RR Lyr の速度分散を 50 km/s とした。Wielen 1974 は近傍準矮星に対し 65 km/s を得た。Eriksson 1978 は彼の SGP 方向視線速度分布を解釈するため 3 % の星が速度分散 70 km/s を有すとした。 太陽近傍の「厚い円盤」星 Oort 1965 は高メタル(ΔS < 5, [Fe/H] ≥ -1) RR Lyr と長周期 変光星を中間種族 II とした。それらは回転速度が速度分散より大きい。これに 反し、低メタル RR Lyr, 極端準矮星、球状星団は回転速度が小さく、速度分散の 非等方性が大きく、楕円率が小さい。これらが厚い円盤を作るとは思えない。 したがって、「厚い円盤」は普通の円盤・楕円体成分とは異なる成分である。 Rodgers et al 1981 が論じた 高メタル A 型星は別の問題である。 |
|
測光視差に基づく近傍光度関数の決定 南銀極 I = 18.0 までの 12,500 星に測光視差を与えて太陽近傍光度関数を定めた。 銀河面高度による光度関数の変化も調べた。その変化を z = 0 まで外挿して Mv = 19 までの光度関数を定めた。それから、輻射等級関数と質量関数も導いた。 どちらも低質量側での値が低く、M < 0.1 Mo 星をミッシングマス候補とする ことが困難なことを示す。 上の関係式を使い、近傍主系列星の密度 = 0.038 Mo pc-3 を導いた。 また、M/L = 1.2 である。 光度関数の特徴 光度関数の形は高度と共に変化する。Mv & lt; +4 の星の星は暗い星に比べ 銀河面集中が著しい。これは年齢と共に速度分散が増加して行くという標準的 見解と一致する現象である。光度関数の形は z > 1000 pc より上では Mv & lt; +4 の勾配が急になるという変化を示す。これはその付近で星種族に 大きな変化が生じ、それより遠くでは古い種族が支配的になることを意味する。 |
厚い円盤 z ≤ 1 kpc では密度則は Mv ≤ +4 星に対してはスケール高 100 pc の指数関数で、それより暗い星では 300 pc スケール高でよく近似できた。 z = 1 - 5 kpc ではスケール高 1450 pc がよい。これら3つの円盤を、若い円盤、 古い円盤、厚い円盤と呼ぶ。厚い円盤の密度則と光度関数の形から、これは楕円体 成分の中間種族 II の星からなると考えられる。 Bahcall, Soneira モデルは観測と大きな不一致をもたらす。その原因は楕円体 成分の光度関数と密度則が不適切なためである。 銀河面に垂直な構造の新しい描像 銀河面に垂直な構造は、スケール高 300 pc の古い円盤が z ≤ 1 kpc までの みつどを決めている。その先は古くて低メタルの種族が支配的になる。この種族は スケール高 1450 pc の指数関数型でも、指数 -3.5 で扁平度 1:4 のべき乗型でも 同じくらいフィットする。他の銀河との比較からは指数関数型の方がよさそうで、 「厚い円盤」と名付けることにする。この円盤の規格値は約 2 % である。太陽近 傍ではこの成分は中間種族 II と分類され、実際、単に円盤の重力ポテンシャルに 応答した銀河系楕円体成分である。第3の成分は極端種族 II 星と球状星団である。 これははるか遠くまで広がるが 5 kpc 以内では数 % 程度の寄与しかしない。単純 な2成分モデルはこれらの結果と合わない。 |