|
銀河系炭素星ミラの絶対輻射等級と視線速度を使ってその運動学を調べる。
銀河系微分回転から周期-輻射等級関係を導き、それが LMC からの P-L 関係と
合うことを確認した。銀河系ミラに対しては Mbol = -2.54 log P + 2.06(±0.24) を得た。ただし勾配は LMC 値を使用した。 | 速度散布度に Nordstrom et al の観測データとパドヴァモデルを合わせて 解析した結果、炭素星ミラの平均年齢 1.8±0.4 Gyr, 平均初期質量 1.8±0.2 Mo を得た。速度散布度の周期による変化が見出された。 周期が初期質量と年齢に依存することを示唆する。O-リッチと C-リッチミラ の関係を論じ、両者の比と様々な星系種族との関係を考察する。 |
| br> これは炭素星ミラ3部作の最後である。 炭素星の年齢と初期質量に関して、 Claussen, Kleinmann, Joyce, Jura (1987), Groenewege, van den Hoek, de Jong 1995 の仕事はあるが、観測による直接 証拠としては、Nishida et al 2000 と van Loon et al 2003 の LMC 星団 の観測くらいしかない。 | 未だに、年齢と初期質量が周期に関係するかどうかの証拠はない。 |

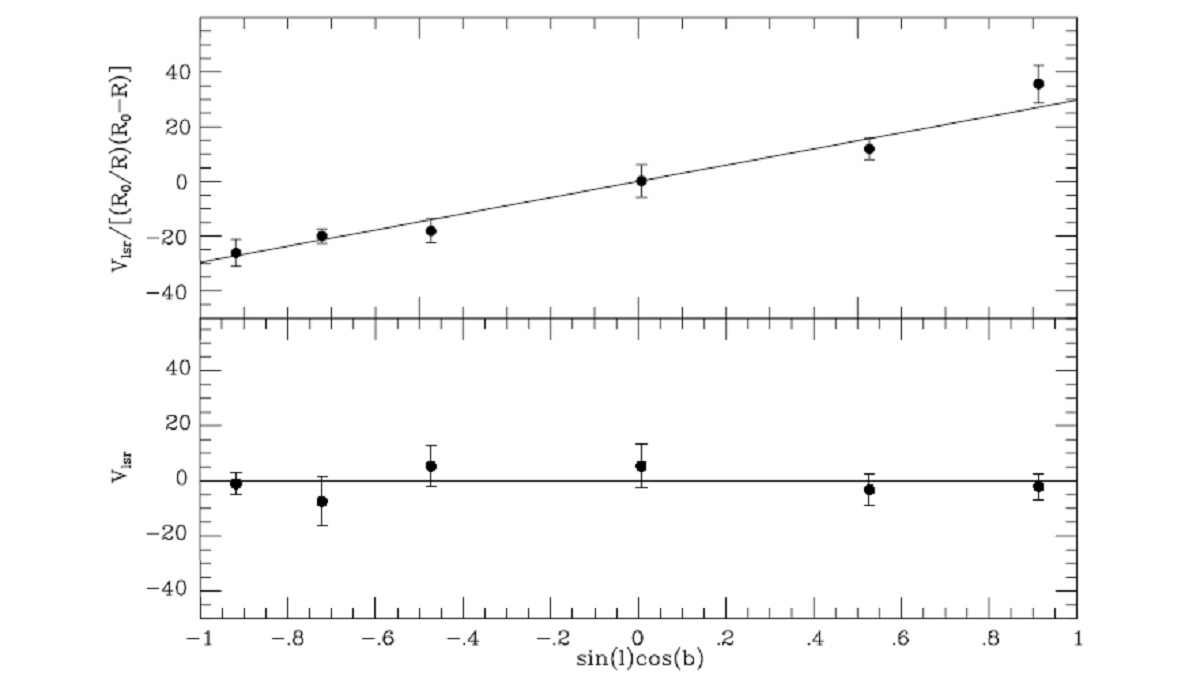
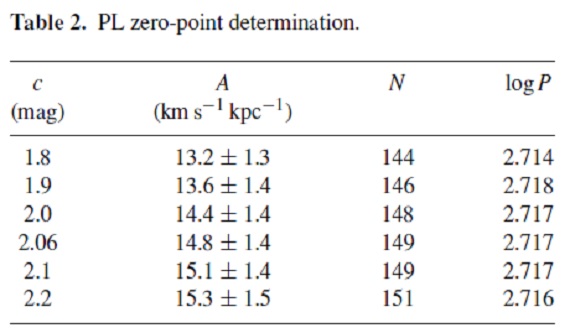 表2.PLR ゼロ点の決定 太陽運動 ここで用いる視線速度は論文II, Menzies, Feast, Whitelock (2006) から採った。使用した太陽運動は uo = +9.3 km/so vo = +11.2 km/so wo = +7.6 km/so である。Feast, Whitelock 1997, Feast (2000) u は GC 方向にプラスを取ることに注意。 距離 太陽からの距離は次の PLR から定めた。 Mbol = -2.54 logP + c DM(LMC) = 18.50 とすると c = 1.87 となる。この c を使った距離が Menzies, Feast, Whitelock (2006) に載っている。この論文の目的の一つは銀河系ミラに対し c を決めることで ある。 微分回転 銀河系微分回転は次の式で表される。 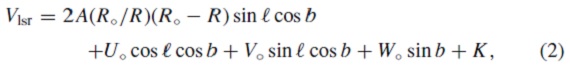 ここに、Vlsr = LSR に対する視線速度。Uo, Vo, Wo = 群運動の LSR に 対する速度成分。K = 可能性のある系統効果。 Ro = 7.62±0.32 kpc Eisenhauer et al 2005 を採用する。オールト定数 A = 14.82±0.84 km/s/kpc は Feast, Whitelock 1997 でヒッパルコスセファイドの固有運動 から導いた値である。 |
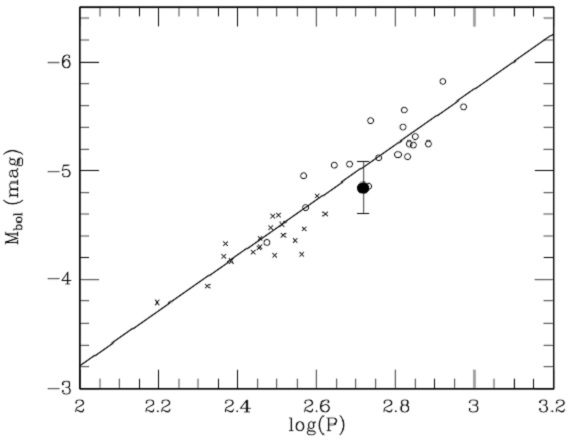 図2.PLR. バツと白丸=LMC C-ミラ。黒丸=銀河系炭素星、平均 log P =2.717に相当。 (MW は一点!しかもこの L は? ) 式2は、星群の運動が円盤状の各点 での微分回転と一定速度 (Uo,Vo,Wo)の足し算であると述べている。静止空間から 見て一定速度とか、別の独自変化則を示すというなら分かるが。これはちょっと? 図1上=オールト定数 A 図1上には銀河円盤の微分回転がはっきりと表れている。表1には式1を 最小二乗法で解いた結果を示す。表1の結果から Uo,Vo,Wo, K = 0 と置いて良い。 表2=ゼロ点の決定 セファイドから決めた A = 14.82 km/s/kpc を採用して、PLR のゼロ点は c=2.06±0.24 となった。 (A=14.82 になる c が 2.06 ってこと? ) 図2= PLR 図2の銀河系炭素星ミラのプロットを見ると、 LMC と有意に違っているようには 見えない。 |
|
速度散布度 c = 2.06 及び A = 14.82 を採用し、さらに Uo = Vo = Wo = K = 0 とすると、 149 サンプル星の各々に対し残差視線速度を計算できる。 あれ、残差視線速度 residual velocity というのは (U, Vo, Wo) + 残差速度=特異速度という意味だったのかな? それらから、α = 銀河中心方向に対する速度散布度と β = GC 方 向に直交する銀河面内方向の速度散布度、それに γ = 銀河面に垂直な 方向の速度散布度を解析できる。サンプル星の大部分は銀河面上に集中してい るため γ の決定は怪しい。 グループ グループ1 P < 470 d グループ2 470 < P < 570 d グループ3 570 d < P 表3に3種類の速度散布度が載っている。 計算条件が異なるのだろうが、本文中にも説明なし。Nordstrom et al. 2004 を 参考にしているらしい。 |
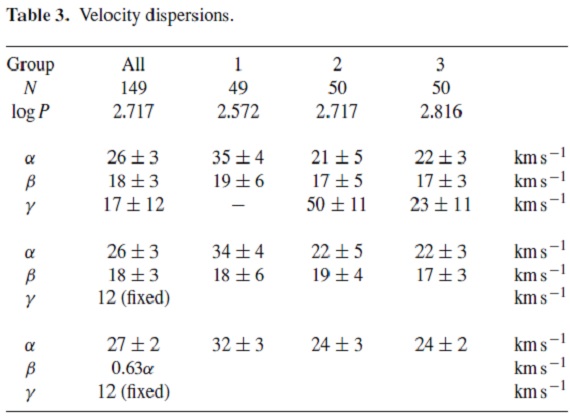 表3.速度散布度 |
|
速度散布度・年齢関係 Nordstrom et al. (2004) は F-, G-型矮星の解析から log σU - log Age 関係を導い た。ここで U 散布度は α に相当する。彼らの関係を直線でフィット し、表3のグループ毎に年齢を定めた。彼らも使用したパドヴァモデル Giraddi et al 2000 を用いて、我々は年齢を初期質量に変換した。その結果を 表4に示す。 年齢 こうして得られた年齢は Nishida et al 2000 の結果に近い。 彼らは TO 質量 1.6 Mo を採用した。これは我々が Girardi00 から得た 1.4 Mo に近い。スケール高から、それよりやや小さい初期質量 1.3 Mo を Olivier, Whitelock, Marang (2001) は得ている。 新しい等時線 Pietrinferni et al 2004 は Giradi00 と異なる新しい等時線を計算した。 その第6章と図8は Giradi00 とかなり異なる。Girardi の 1.8 Gyr 等時線は Pietrinferni 2.5 Gyr 等時線と酷似する。Pietrinferni モデルの TO 質量は 0.4 Mo 大きい。 |
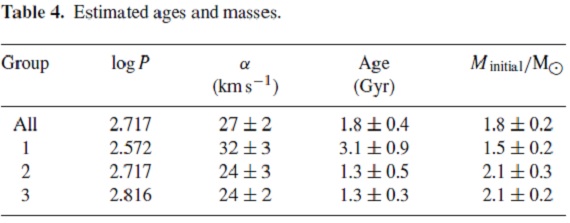 表4.炭素ミラ型星の年齢と初期質量 (よく分からない。等時線が似ているのに、 つまり HR図上で同じところにある TO がモデルにより 0.4 Mo も異なる質量に対応 するのか?しかも、 Piertrinferni の方が 2.5 Gyr で高齢なのに、TO 質量が大きい ってどういうこと?) この差は、Pietrinferni によると、入力物理とオーバーシューティングの扱いに 原因がある。 周期年齢関係 表4の結果からはグループ2と3の間に年齢の差はない。しかし、全体と しては周期が長くなると年齢は若くなるという傾向にはある。O-リッチミラ に関しても、同様の傾向は存在する。 Feast, Whitelock (2000) |
|
表5=O-ミラ Feast (1963), Feast, Whitelock (2000) は O-ミラの非対称ドリフトと速度散布度が周期と共に変化することを示した。 表5には速度散布度 α を O-ミラの周期グループ毎に示す。 C-ミラとの比較のため、α と β/0.63 の平均を取った。 O-ミラの年齢 高メタル球状星団の短周期ミラ Feast, Whitelock, Menzies (2002) も合わせると、O-ミラの年齢は短周期の端に当たる球状星団年齢から長周期 側では 450d 周期ミラに相当する 2 Gyr まで、それに OH/IR 星のもっと 若い集団に分かれるだろう。表5の最後の列は各周期グループに割り振った 年齢を示す。表4と比べると、 Feast, Whitelock (2000) で扱った O-ミラは C−ミラと較べ、高温で高齢の星であると分かる。 O/C 比と年齢:太陽近傍 Wood, Cahn (1977) は太陽近傍可視ミラのサンプルを調べ、O-ミラの数が C-ミラの 14 倍とした。 可視ミラは短周期ミラに重みが掛かる。より長周期のダスト星に関して、 Olivier et al. (2001) は O/C = 1 であることを見出した。ある星集団における O/C 比は年齢に依存 することは明らかである。従って、単純に O/C 比がメタル量で決まると 言うことは出来ない。 バルジの C/O 比 前の2段落での議論から、 C-ミラ/O-ミラ 比は年齢に依存することが示唆 される。しかし、この比に影響する他のファクターもある。バルジの O-ミラ の周期はバーデまでで 700 d にまで及び、 GC 付近ではさらに長周期のミラが 見つかっている。それに反し、C-ミラはない。過去にはそれはバルジが高メタ ルのせいであると考えられた。King 1993. しかし、現在ではバルジと太陽近傍 円盤のメタル量は似ていると考えられている。表4と表5を較べると、 C-ミラとグループ7O-ミラは同じ運動学特性を有し、 したがって、ほぼ同一の年齢と考えられる。 (何が分けるのか?メタル量? ) |
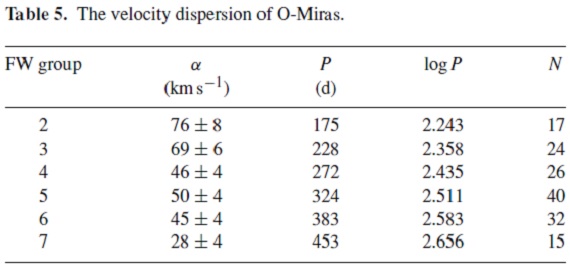 表5.O-ミラの速度散布度。 バルジにもグループ7と同じ周期帯の O-ミラがあるが、C-ミラはない。つまり、 メタル量も恐らく年齢も同じなのに、円盤には C-ミラがあり、バルジにはない。 [O/Fe] が決め手だった Glass et al. 1995 はバルジミラの JHK カラーが LMC と異なることを見出 した。これは Feast (1996), Feast, Whitelock 2000b によって、H2O バンドが強いためであると 説明された。さらにその原因は、バルジ星のO−組成(α 元素)が2.5 倍 大きいためである。Rich, Origlia 2005 は実際バルジ M-巨星で [O/Fe] = +0.3 であることを示した。それとは逆に LMC では [O/Fe] が低い。このように バルジの O-組成が高いことが TDU による O/C 比逆転を妨げているのである。 O/C の要因 ここまでの議論からミラ型星の、そして多分巨星で、 O/C 比は、メタル量、 年齢、 [O/Fe] の関数として決まると思われる。そして、銀河系の薄い円盤 では炭素星のメタル量はやや低い方に傾ているのかもしれない。 |
|
V CrB C-ミラ V CrB は (u, v, w) = (28, -67, -92) km/s で w の大きさで有名 である。この星はまた、[M/H] = -1.35, [Fe/H] = -2.12 という報告がある。 二つの間の差が大きいことは分光解析の困難さを物語る。それにも拘わらず この星の低メタル量は確かであろう。extragalactic interloper の 可能性がある。Ibata et al 2001 はハローにもそのような interloper が いると述べている。 バー運動? 表6には銀河回転からのずれが 50 km/s を越える星を載せた。興味深いのは GC 方向にある4つの炭素星と Anti-Center 方向の一つの星である。 それらは全て銀河中心から外向きの運動を示している。これが単なる統計効果 かどうか調べるのは面白い。 O-ミラのバー的な運動 Feast (1963), Feast, Whitelock (2000), Feast (2003) との関連も興味ある問題である。 |
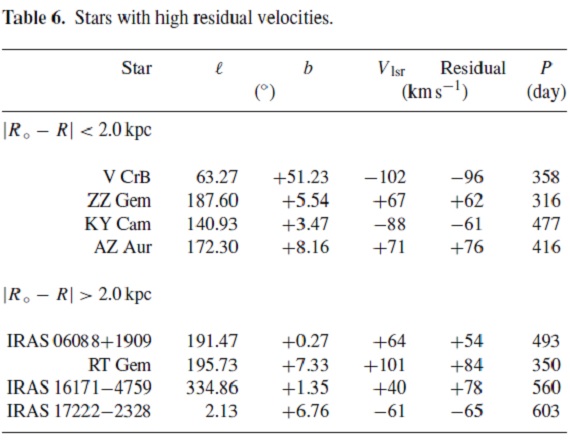 表6.高速炭素星 |
|
C-ミラの周期光度関係 LMC C-ミラと同じ勾配を仮定して近傍 C-ミラの周期光度関係のゼロ点を 定めた結果、誤差の範囲内で同じ値であった。この結果は銀河への応用で 重要である。場合によっては NIR データしか得られないがその場合輻射 補正が使える。 C-ミラの年齢と初期質量 我々のサンプルの範囲内で C-ミラの年齢と初期質量は限られた範囲に 限定されると分かった。我々が見出した低質量と中間年齢はマゼラン雲星団で 得られた値と合う。 星形成爆発? かなり高い初期質量が提案されたことがある。 Bergeat, Knapik, Rutily 2002 は 4 Mo と主張した。Raimondo et al 2005 は CMC の LPVs の大部分no 年齢が 0.3 - 0.5 Gyr であると述べた。これは我々の推定年齢よりかなり若い。 Raimondo et al 2005 はそれらが Harris, Zaritsky 2004 の提案する星形成 爆発の時に出来たと考えた。我々の C-ミラ年齢は敢えて合わせればむしろ 2.5 Gyr 前の星形成爆発に近い。 |
星形成史 我々の結果をマゼラン雲での結果と考え合わせると、C-ミラがそれらが生ま れた星種族、例えば系外銀河、の平均年齢を与えるようだ。さらに、初期質量 と年齢は周期の関数であるらしい。したがって、C-ミラの分布は 1.5 - 3 Gyr における星形成史を与えるであろう。 速度散布度 速度散布度から、与えられた同じ周期では C-ミラの光度は O-ミラより暗い。 ただし両者の SED は大きく異なり系統誤差が関与する可能性がある。 |