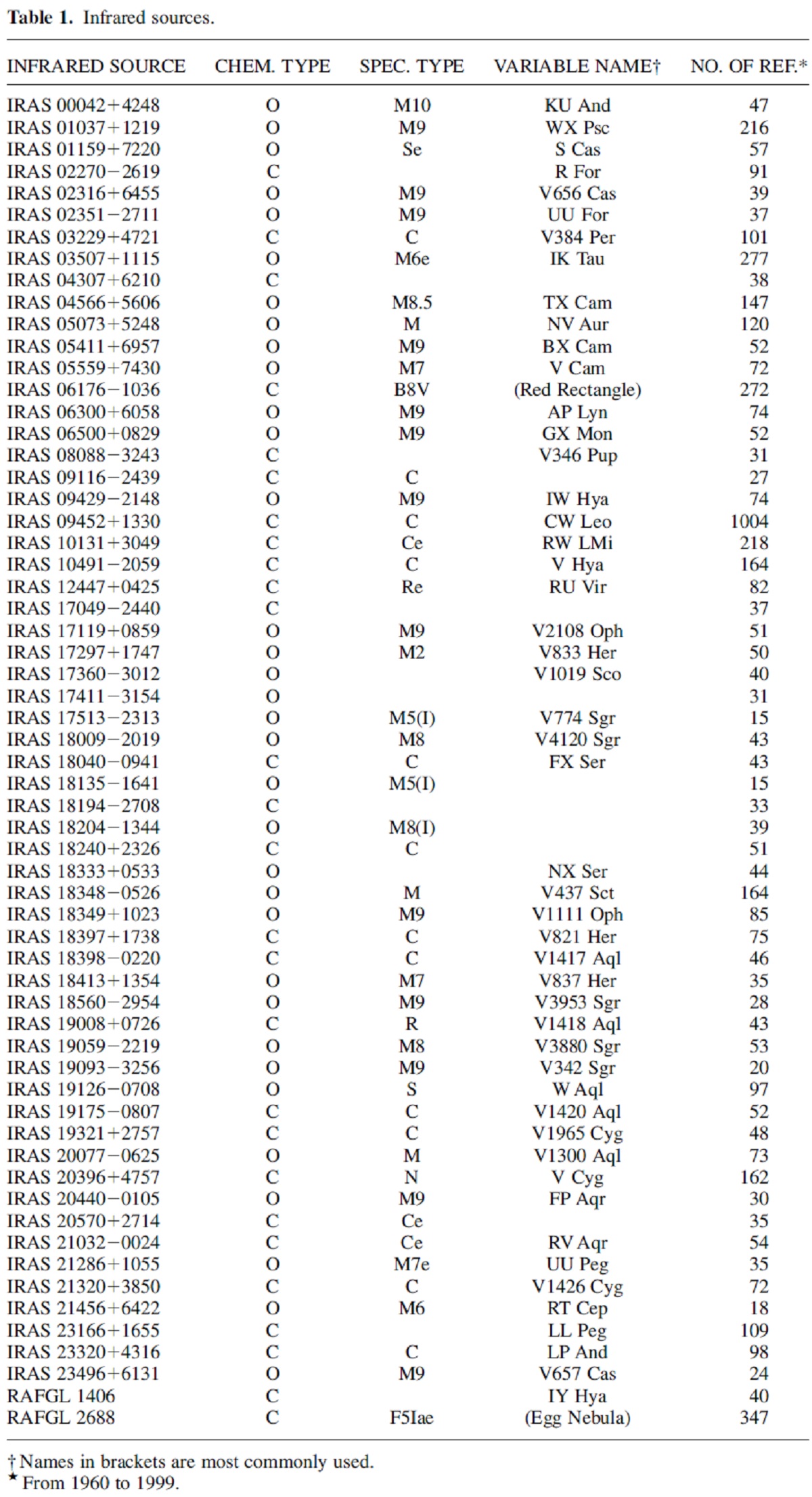
| ダストに埋もれた 58 個の AGB 星、内二つは post-AGBs の可能性がある、 を調べた。27 個は C-リッチ、21 個は O-リッチである。これらは、 Jura, Kleinmann (1989) の太陽近傍高マスロス AGB 星(dM/dt > 10-6Mo/yr)に載って いる星である。NIR 地上測光、IRAS、視線速度と流出速度データを合わせてこ れらの星の性質を解析した。NIR 変光振幅は周期と相関し、波長と共に減少す る。P < 1000 日での統計テストからは C-リッチと O-リッチで周期分布に 差があると考える根拠はない。 | 周期 1000 日を越える炭素星はない。PLR を用いて光度と距離を決めた。 F60 から決めたマスロス率は赤外カラーと周期に相関する。 相関が強いのはマスロス率と k-[12] カラーの関係である。サンプルの運動と スケール高は周期 1000 日以下の星は低主系列質量星であることが判る。 O-リッチで周期が 1000 日を超す3つの星は中間質量星かも知れない。他の 星の平均質量は 1.3 Mo で白色矮星質量は 0.6 Moであろう。高マスロス率期 間は 4 104 年と見積もられ、これらの星が AGB を離れる前に TP を経験するとしても精々1回である。 |
|
SAAO NIR モニタリング Jura, Kleinmann (1989) は 1 kpc 内のマスロス AGBs を定めた。SAAO では 1989 年からそれらの星で 観測可能なものの JHKL モニタリングプログラムが開始された。 |
この論文 この論文では SAAO 測光の結果を他の情報と合わせ、サンプル星の性質を 調べる。 |

|
JK89 の選択 Jura, Kleinmann (1989) の目的は近傍 AGB 星からのマスロスをより定量的に調べることであった。彼ら は 1 kpc 以内にあり、 δ = [-33, 82] の 10-6 Mo/yr 以上 の AGB 星を同定した。彼らは TMSS, IRAS, AFGL に基づいて 63 天体を選んだ。 見直し 3 Pup は超巨星である。 NGC7027 は AGB でない。 IRAS 17513-2313, 18135 -1641, 18204-1344 は M-超巨星、なので外す。 表1 C/O 区分は Loup et al 1993 から採った。51 星のスペクトル型は Simbad から採り、表1に載せた。04307+6210 は Simbad では M6 とされているが Groenewegen 1994 は炭素星であることを示した。超巨星は "I" を付けた。 |
最終サンプル 最終サンプルは 27 炭素星と 31 O-リッチ星から成る。O-リッチには 二つの S-型星が含まれる。 メーザー Benson 1990 のメーザーカタログには 20/28 で OH, 20/28 で H2O, SiO を探した 21 星中 19 で検出された。面白いことに SiO を探した 11 炭素星中 4 つで検出されている。 |
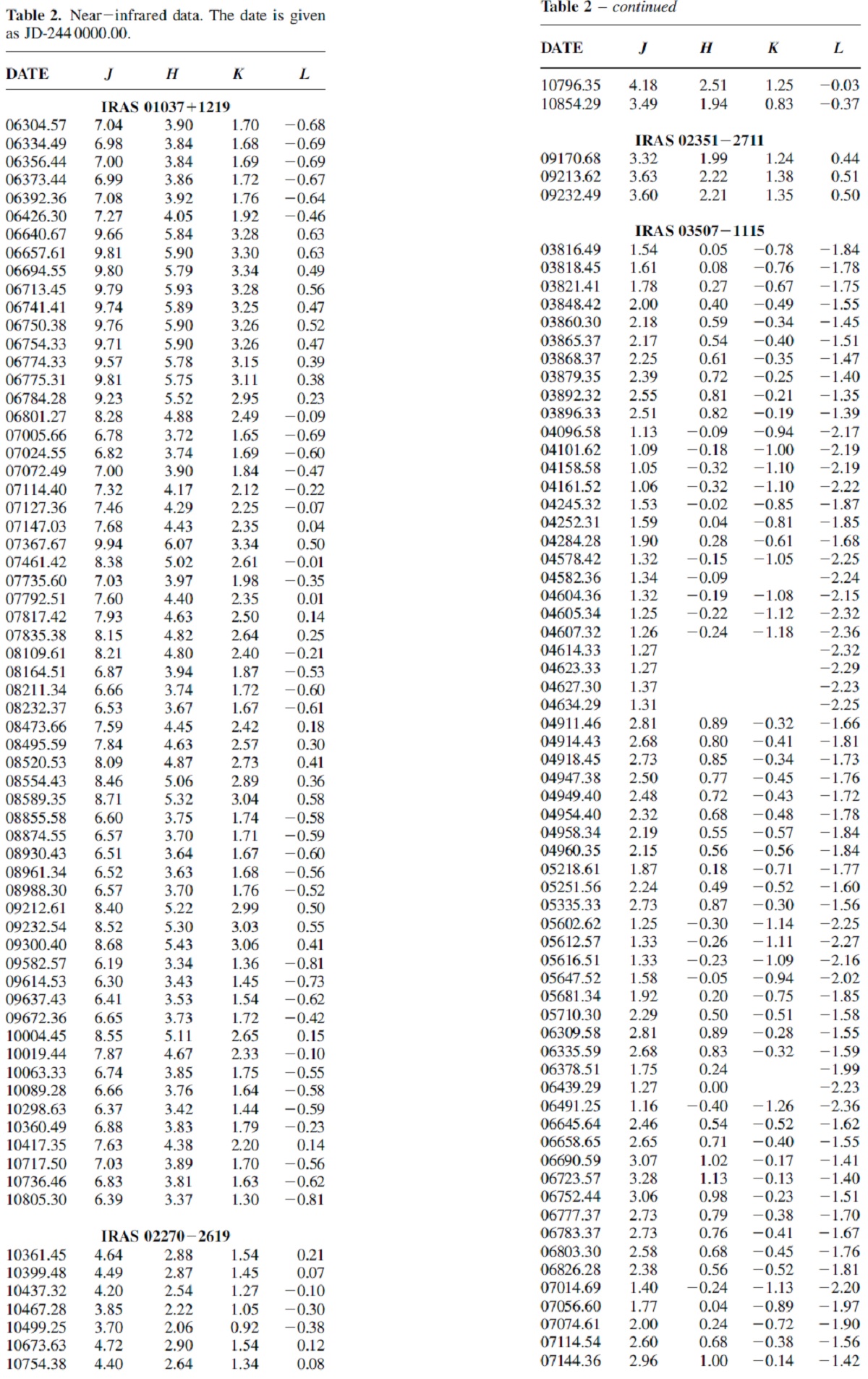
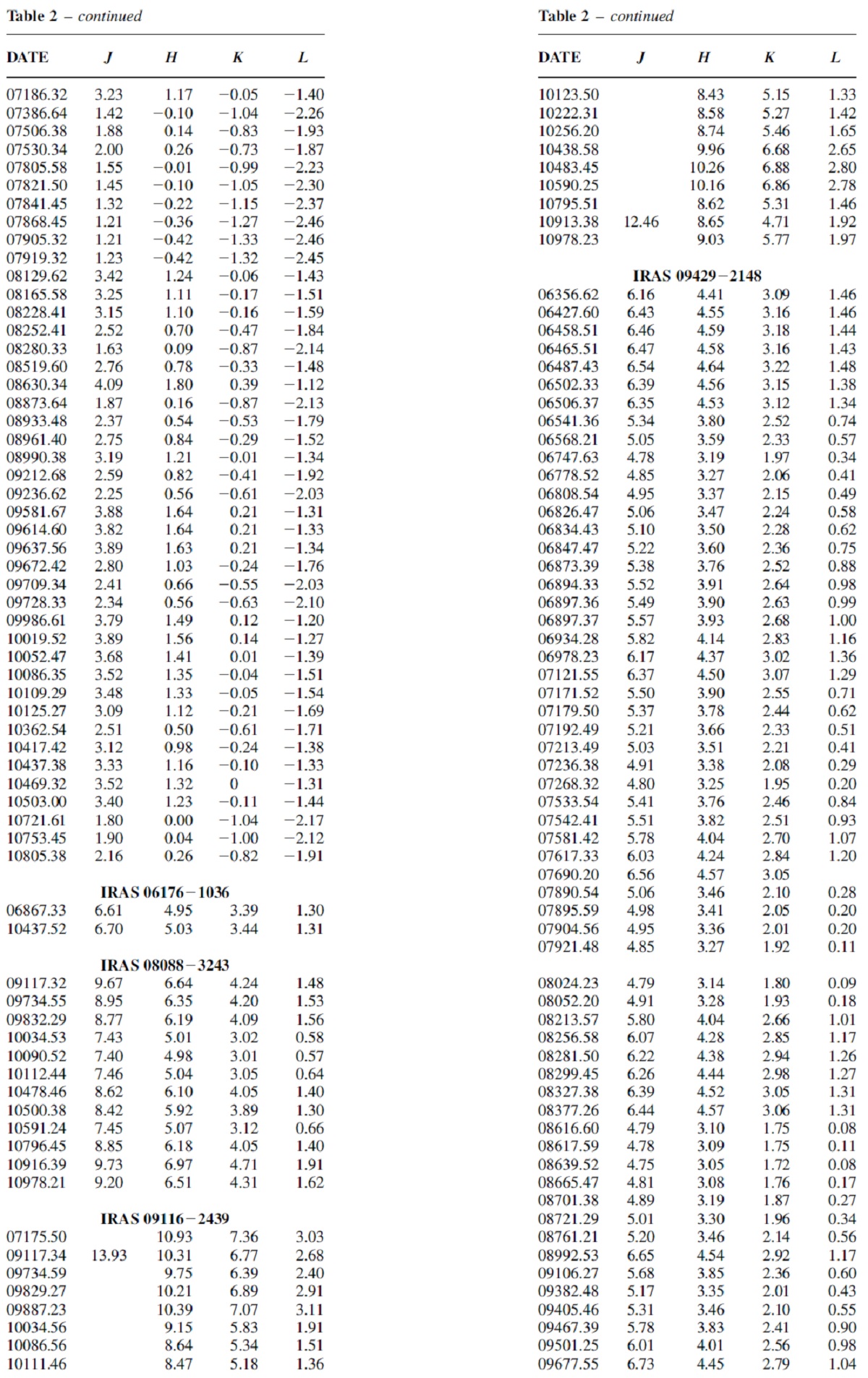
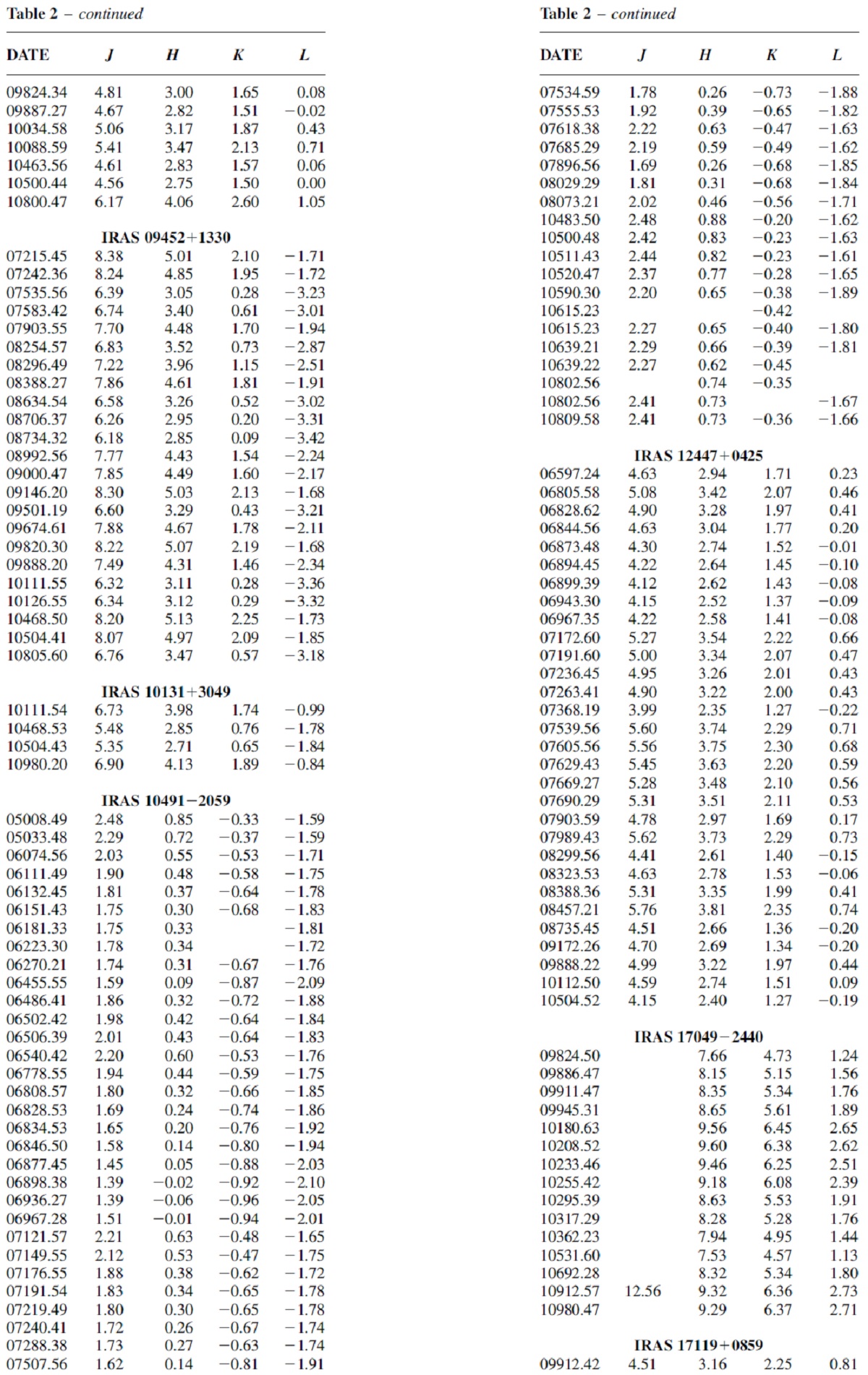
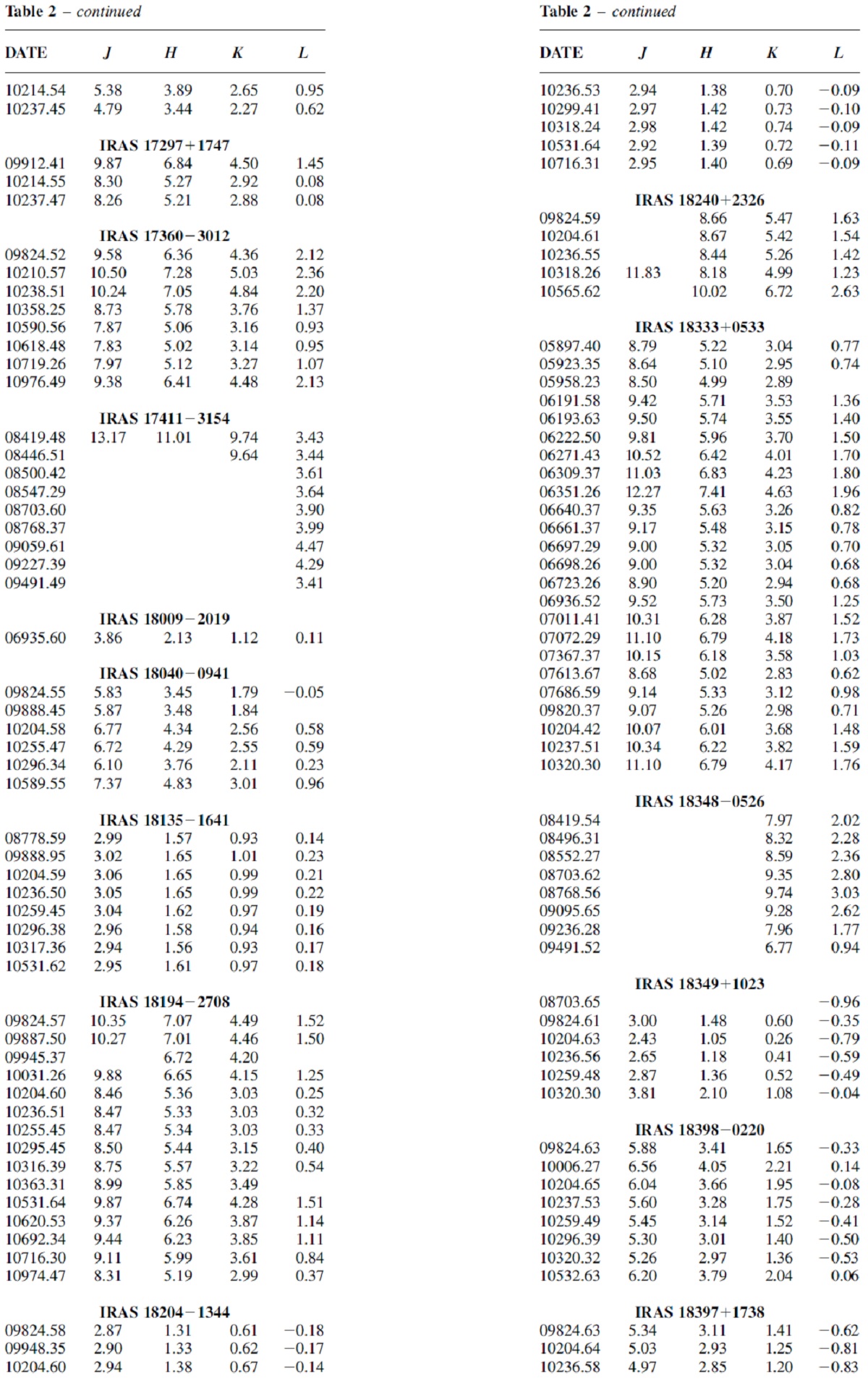
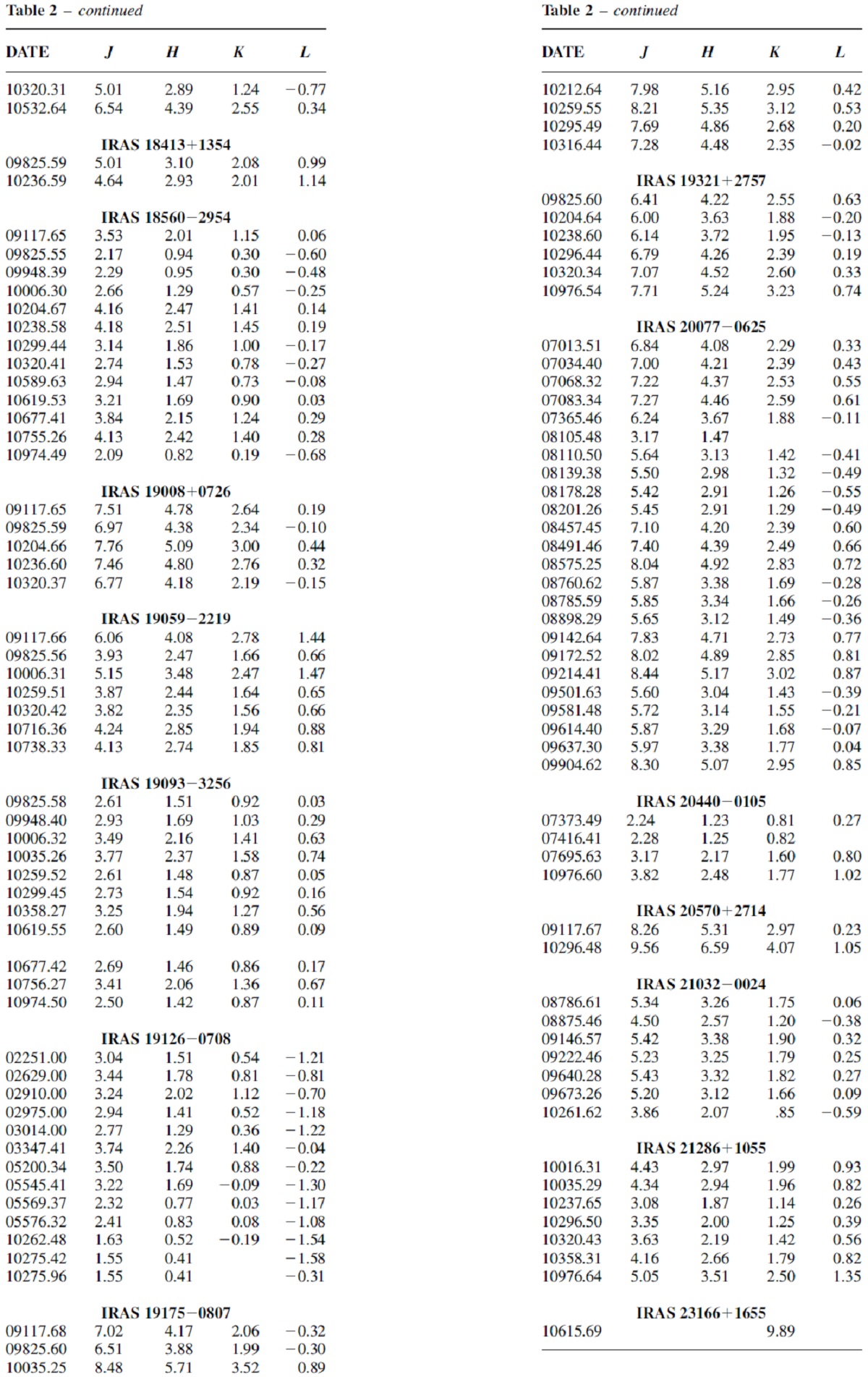
表3.平均 NIR 等級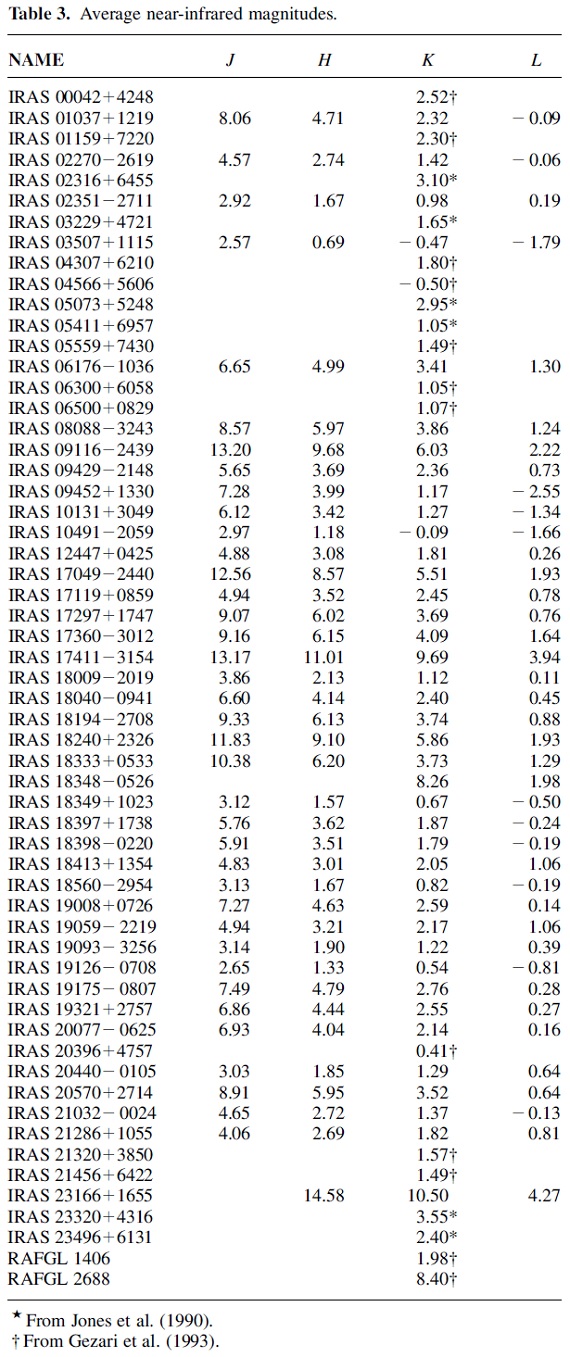 |
|
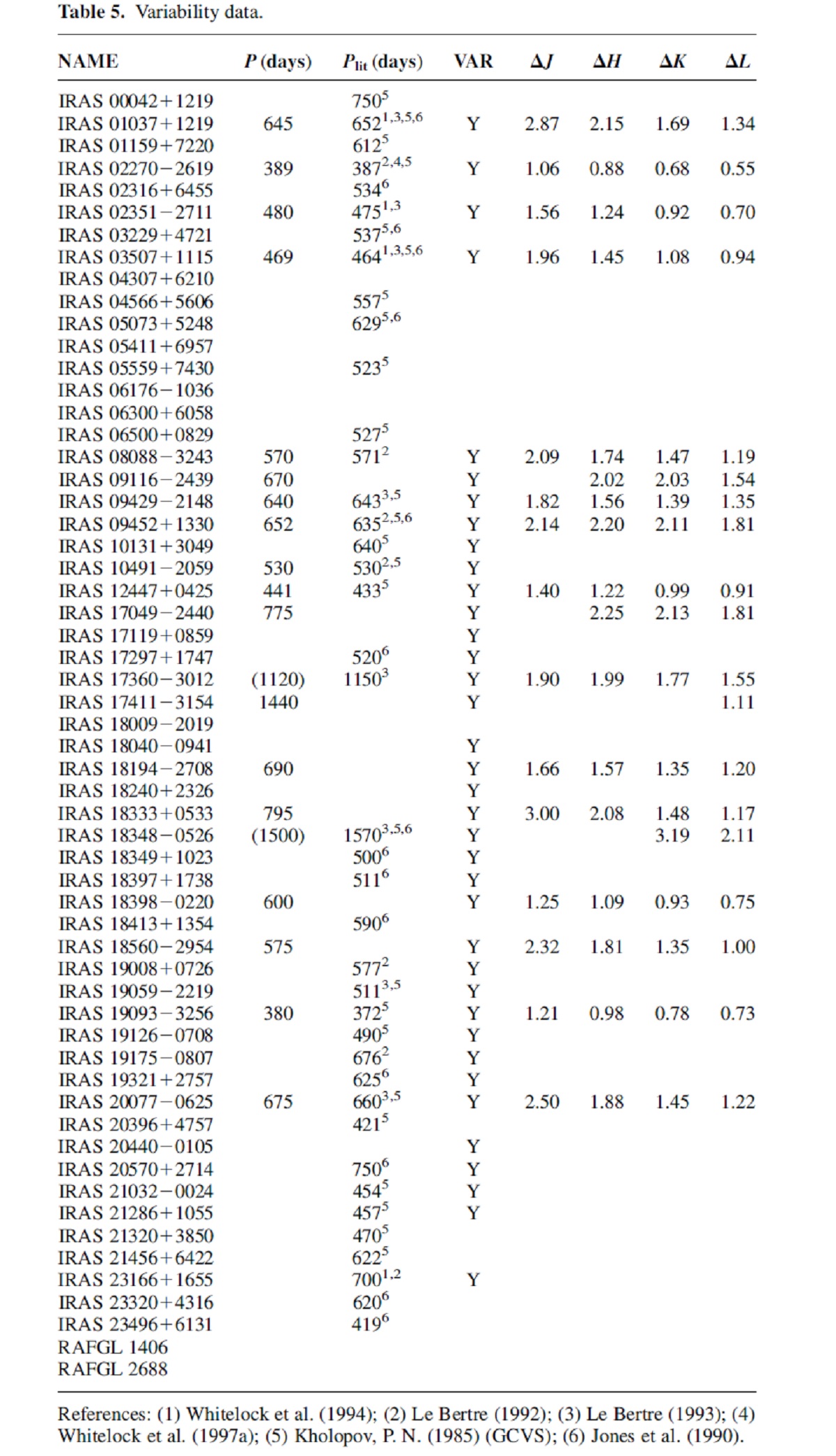
NIR 測光観測 南天 45 星中 42 星の NIR 測光観測を行った。IRAS 0650+0829, 17513-2313, RAFGL 1406 は混み合った星域にあり測光が出来なかった。 K で 0.1 mag 以上の変動があったら変光星と定義する。 IRAS 18135-1641 と IRAS 18204-1344 は非変光星であるが、超巨星でもある。 表5=変光のまとめ 表5に変光観測の結果をまとめた。 |
周期 10観測点以上のデータある星は K 測光へのフーリエ変換から周期を決め た。非常に赤い IRAS 17411-3154 の周期は L 測光から決めた。表5に あるように 20 天体の周期が決まった。それらの折り畳み変光曲線を 図1に示す。 |
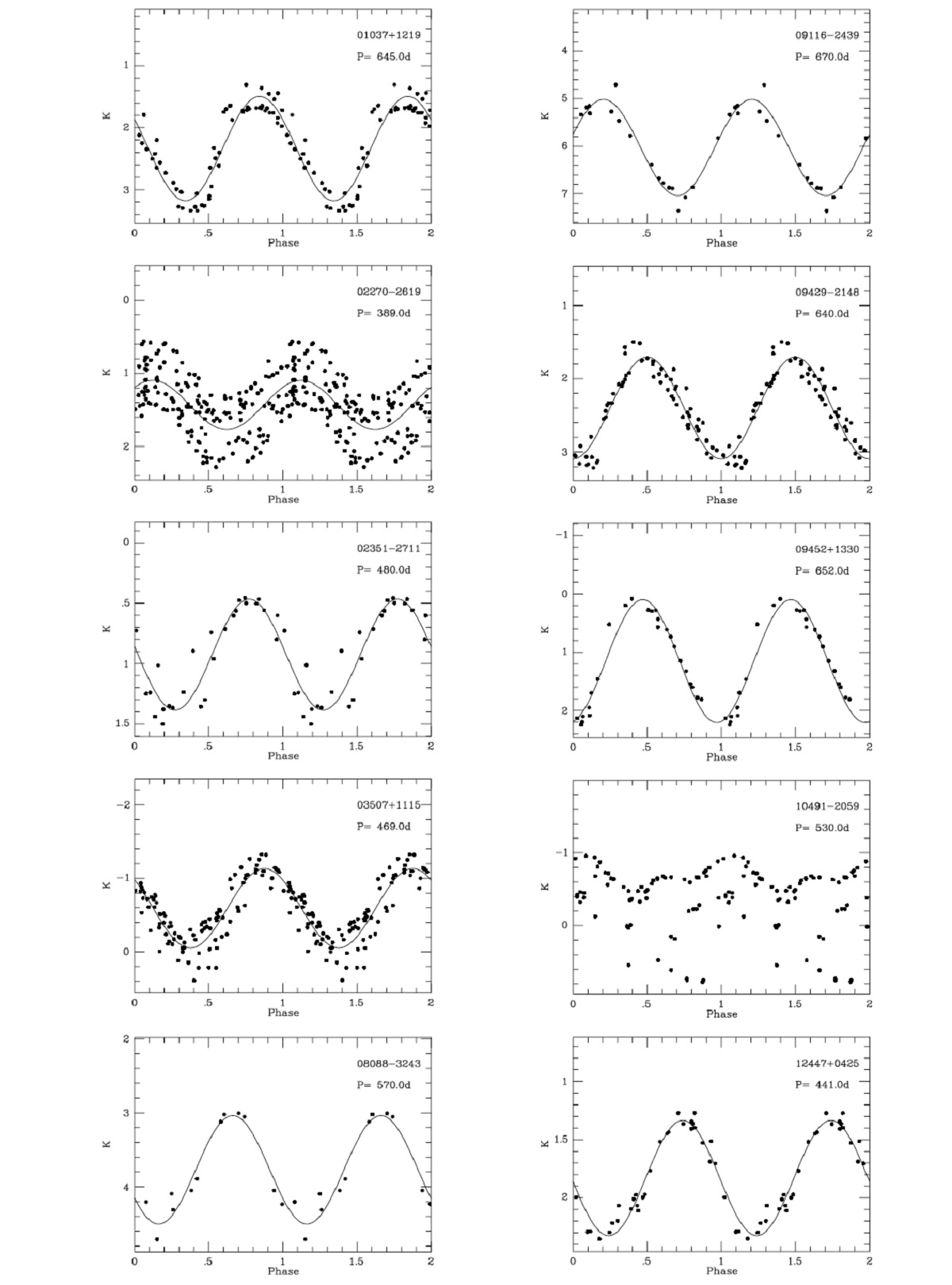
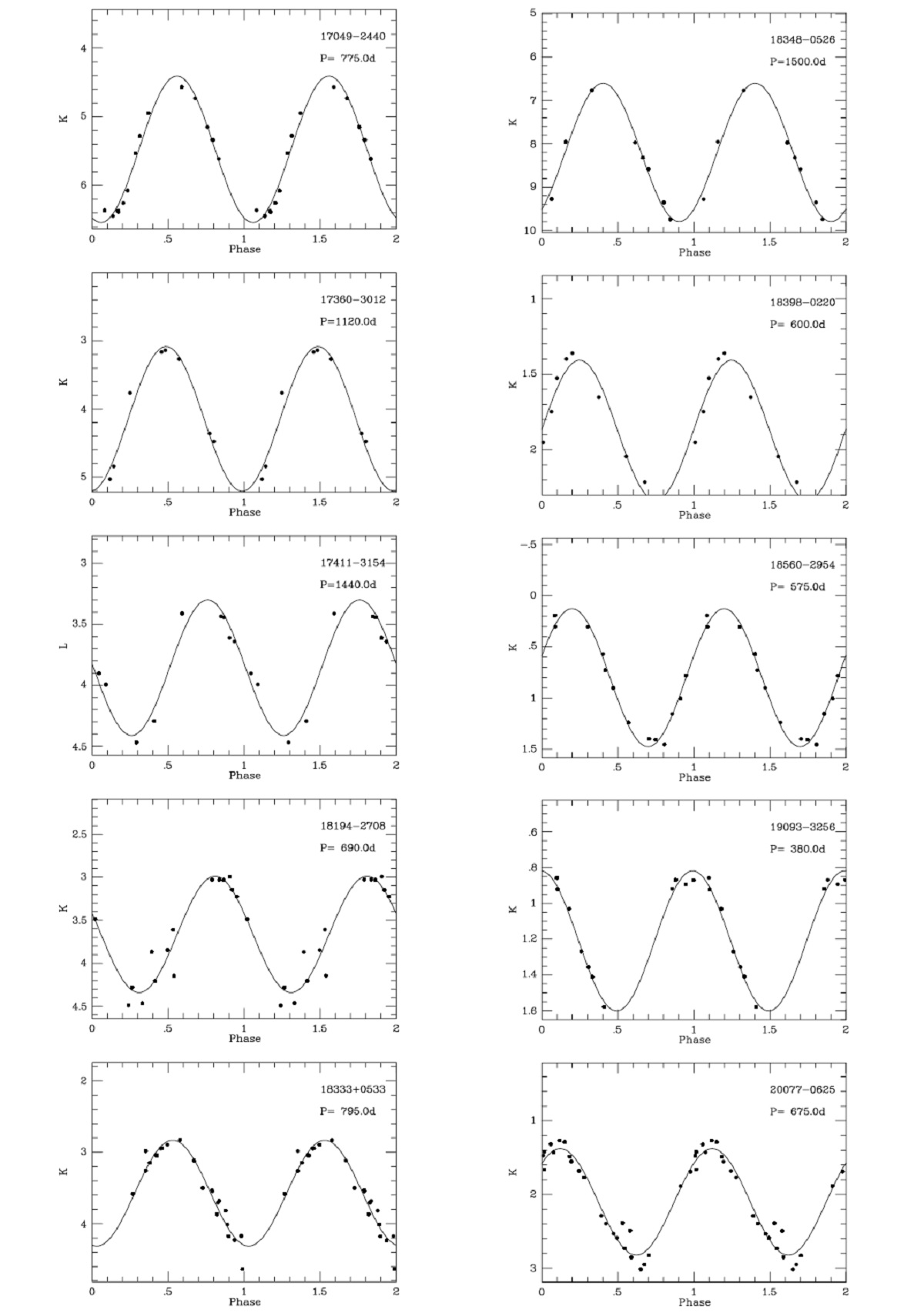
4.1.折り畳み変光曲線図1=変光曲線位相ゼロ点を JD 2440000.0 として、20星の折り畳み変光曲線を作成し、 図1に示す。次式で最小二乗フィットした。 M = (ΔM/2)sin(φ-φo) + Mav ただちに気付くように、ばらつきが大きい。理由はいくつかあるが、 (1) 変光が完全に規則的ではない。 (2) 特に炭素星では一時的減光現象が起きる星がある。Whitelock 1997 R For) を見よ。 (3) 非常に数少ない星では、光度、周期、振幅に長期変動が見られる。 4.1.1.V HyaV Hya図1の中で最もおかしな変光曲線を示すのは V Hya である。この星は双極型 の流出流を持ち、回転または連星が疑われている。 図2=変光曲線 図2aに V Hya の実時間変光曲線を示す。V Hya は JD 2443500 と 2449500 付近で減光現象を起こしている。 JD [2446000, 2448250] 期間のデータは P = 530 d を示し、 GCVS と一致する。図2b にはこの期間の折り畳み変光曲線を 示す。 超長周期変光 Knapp et al. 1999 は AAVSO の 3260 実視等級 (35 年間)を解析した。彼 らは Mayall 1960 が定義した 6160±400 d の超長周期を再確認した。 図2a に現れた二つの減光はこの超長周期 ΔK = 1.7 mag に整合する。 |
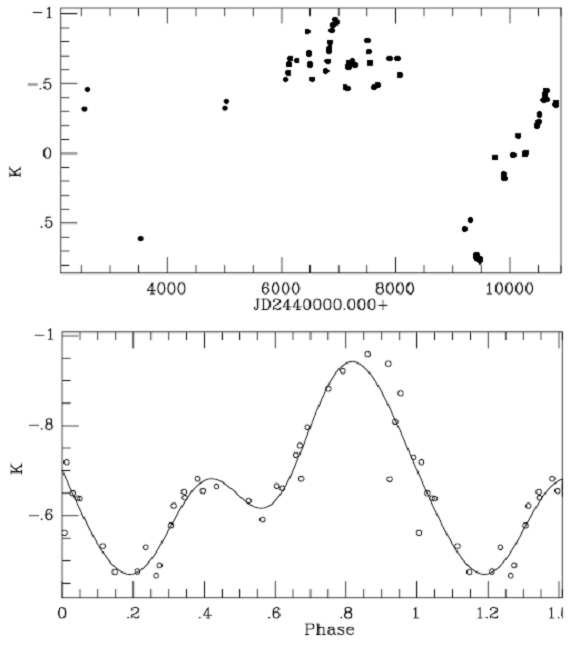 図2.(a) V Hya の実時間変光曲線。(b) 折り畳み変光曲線。JD =[2446000,2448250] |
4.2.周期分布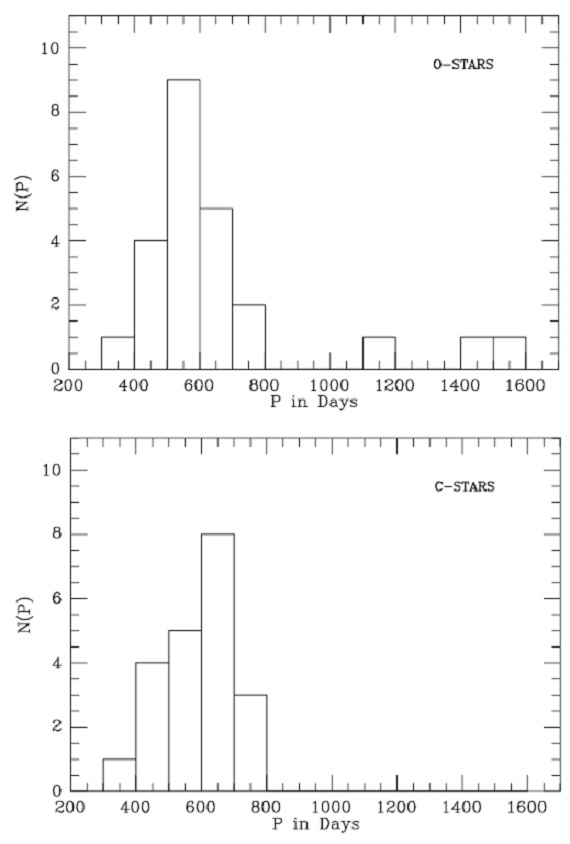 図3.周期分布 |
4.3.変光振幅図3に周期分布を示す。大部分は 500 - 700 d の間にある。 1000 d を超す OH/IRs が三つある。炭素星には 1000 d を超す星は存在しないのであるが、 周期のピークは O-リッチ星よりも長い側に位置する。ただし、コルモゴロフ・ スミルノフ検定の結果は両分布が同じ母集団からの確率は 0.4 であり、 0.05 以上なので炭素星と O-リッチ星が異なる母集団に属するというのは 有意な結果とはいえない。F-検定は分散が同じである確率は 2.5 10-5 と言う結果を与えた。つまりありそうにない。一方、分散も考慮した t-検定は 同じ確率 0.24 を与える。こちらからは違うとは言えない。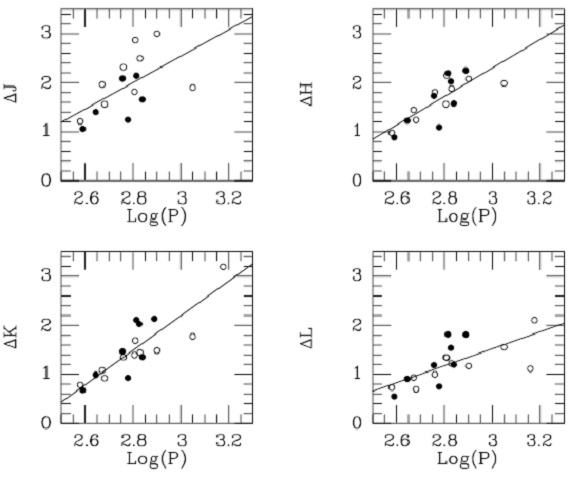 図4.振幅と周期の関係。黒丸=炭素星。白丸=O-リッチ星。 表5には振幅を与えてあり、その分布を図4に示す。明らかに振幅は 波長と共に低下して行く。図4から振幅と周期の相関も明らかである。 統計テストのどれも炭素星とO-リッチ星との間に振幅分布の有意な差を 見出せなかった。 |
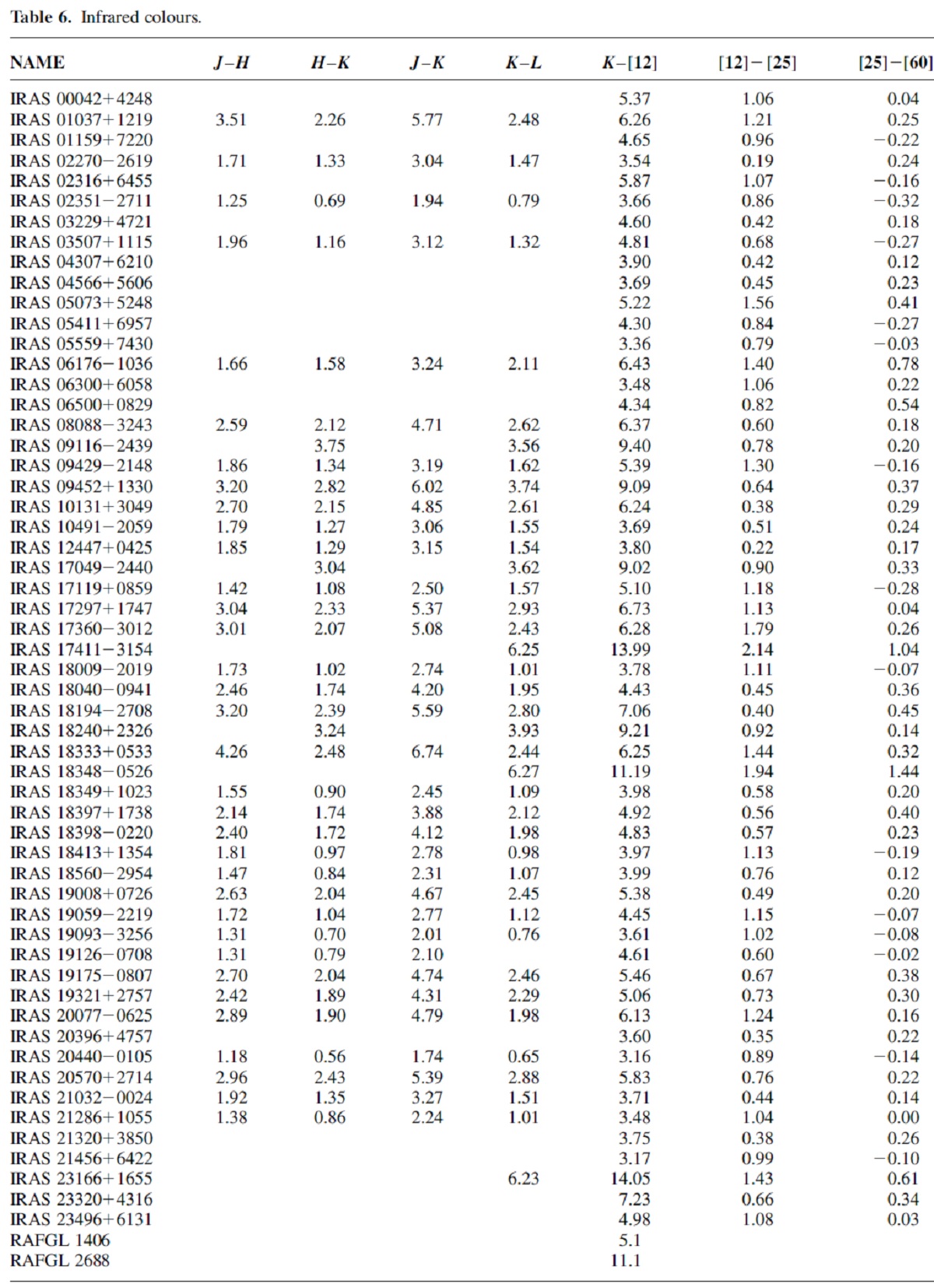
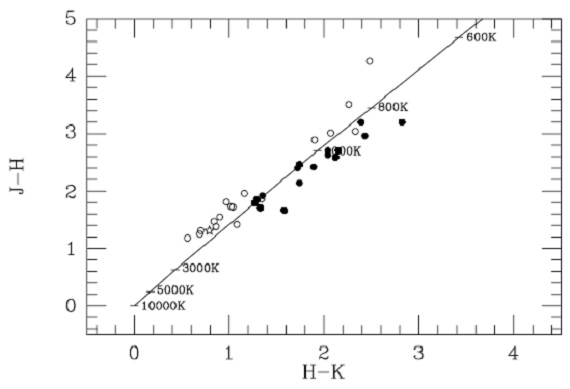 図5.(J-H) - (H-K) 二色図。 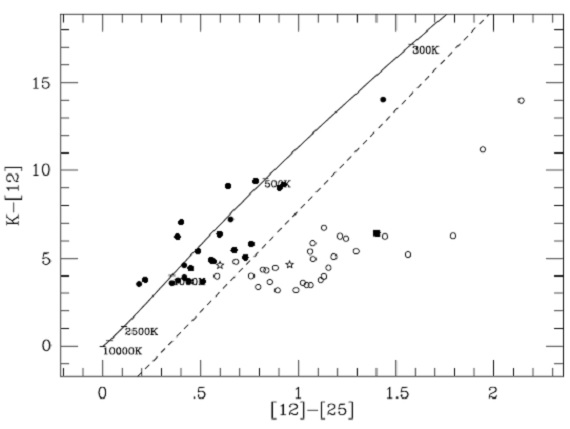 図7.(K-[12]) - ([12]-[25]) 二色図。 図5、7 NIR TCD (炭素星系列が O-ミラの間に 割り込んで見える。質量分離を表しているのか? ) |
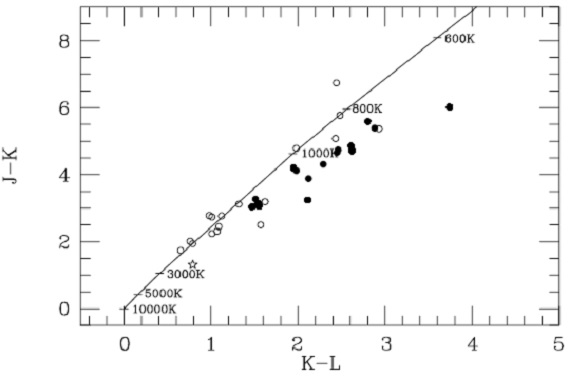 図6.(J-K) - (K-L) 二色図。 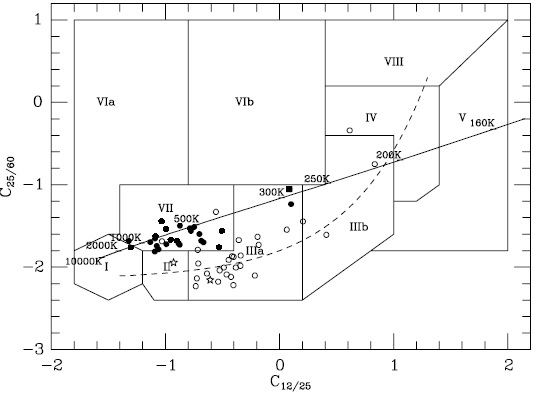 図8.C25/60=2.5log(F60/F25) - C12/25 二色図。 図7 (K-[12]) - ([12]-[25]) 二色図は炭素星と O-リッチミラがはっきり分かれていて 興味深い。この分離は Le Bertre et al. 1994 が既に注意していて、彼らは その原因をオパシティの NIR/MIR 比の差にあるとしている。 |
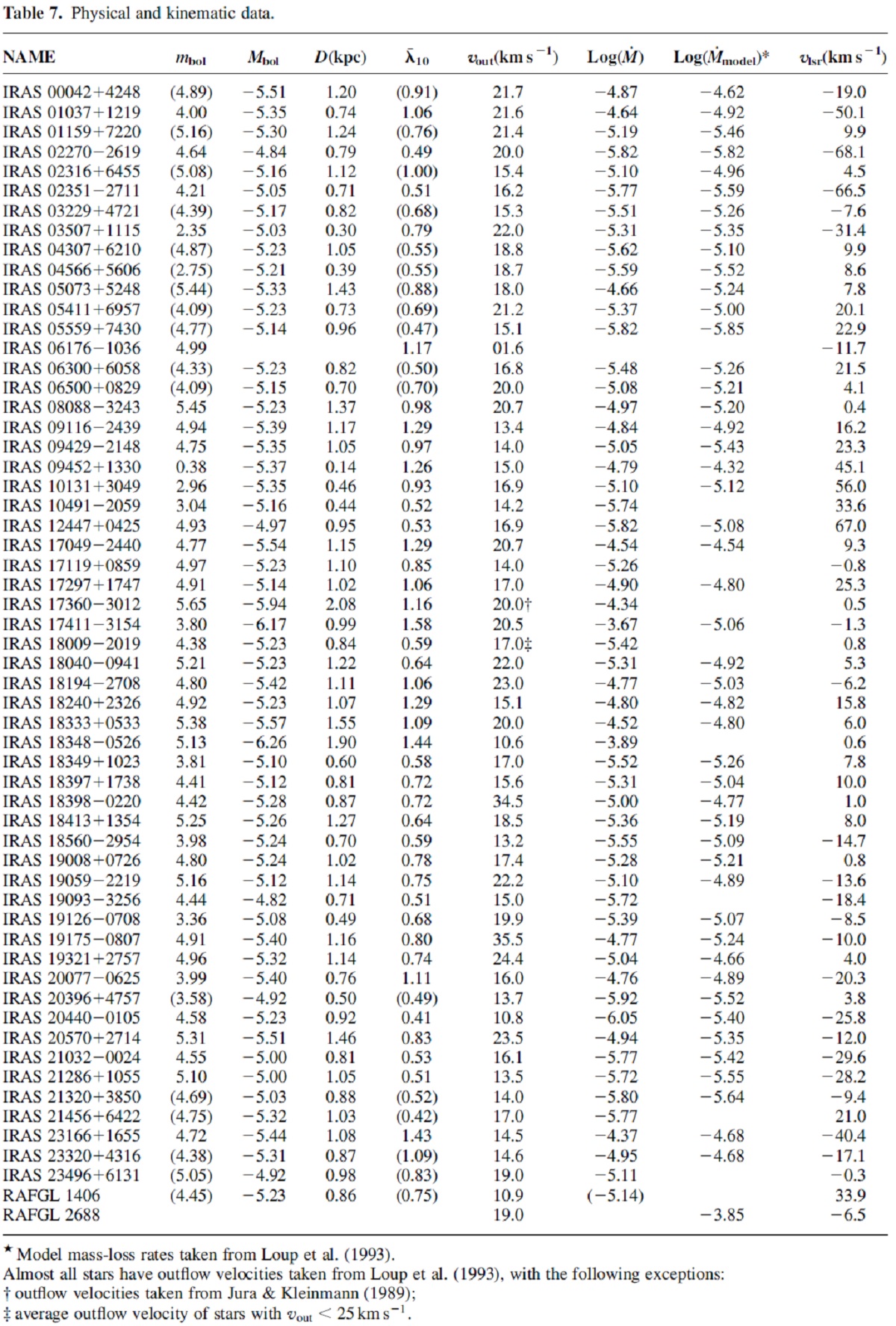
6.1.見かけ輻射等級スプラインフィットmbol の計算には、J,H,K,L,F12,F25 フラックスを ν 座標上で スプラインフィットして求めた。端点からは外挿線を伸ばした。J 点と H と K の中間点を結んだ。ゼロ振動数ではフラックスゼロとした。 輻射補正 O-リッチ(式4)とC-リッチ星(式5)に対する輻射補正を図9に示す。 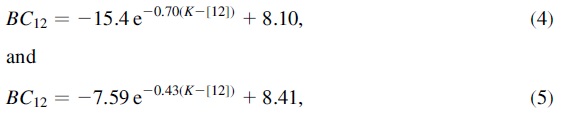 6.2.絶対輻射等級と光度PLR周期の分かった 47 星に対して LMC ミラの PLR と DM(LMC) = 18.60 を仮定 して Mbol を次の式で計算した。 Mbol = -2.34 logP + 1.26 周期 1000 d 以下の星の平均光度は 0.98 104 Lo である。 周期不明の星に対してはこの光度を仮定する。 |
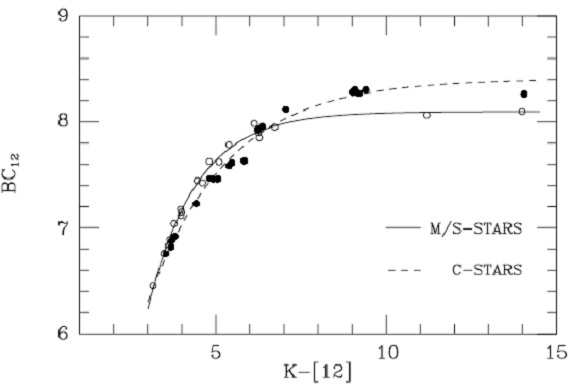 図9.BC12 と K-[12] の関係。 長周期星の光度 先の PLR は LMC P < 420 d のミラの観測から導かれたものであることを 忘れてはいけない。実際、 LMC には PLR より上に位置するミラ型星の例が 報告されている。しかし、それらは HBB による過剰光度のほしであり、一般には 長周期の星も同じ PLR に従うことが判っている。 |
6.2.距離PLR 距離 mbol と Mbol から距離が計算できる。それらを表7に示す。 それらの距離は一般に Jura, Kleinmann (1989) で与えられた距離より大きい。光度は大体同じなのであるが、見かけ光度 が今回の方が小さいことが主原因である。 |
OH メーザー距離 OH/IR 星では位相遅れ法により距離を定めることが可能である。ただそれは 非常に手間が掛かる。今回のサンプル中には二つ位相遅れ法で距離が定まった 星 Van Langevelde et al 1990 が含まれる。その一つ IRAS 01037+1219 (WX Psc) の 0.74±0.15 kpc は表7と同じである。もう一つの IRAS 18348-0562 (OH26.5+0.6) には 1.44±0.27 と 1.30±0.35 の二つの距離が 与えられている。表7の値は 1.9 kpc である。 |
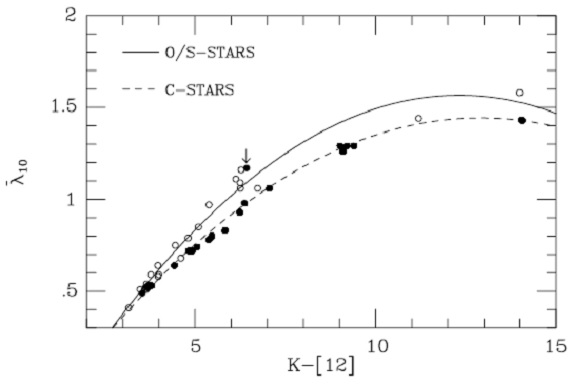 図10.λ10 と K-[12} の関係。 Jura 1987 のマスロス率 マスロス率は Jura (1987) から採った。それは 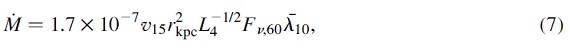  で、オパシティは 60 &mu:m で150 cm2gg, ガス/ダスト比 4.5 10-3 Jura 1986 を仮定している。 図10のフィットから、 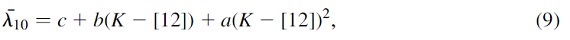 という近似式を用いた。O-リッチ星で (a, b, c) = (-0.01, 0.284, -0.392), 炭素星で (-0.0137, 0.338, -0.513) である。 星風速度 図11には星風と Mbol の関係を示す。相関はない。 マスロス率の比較 図11では、マスロス率を Loup et al 1993 の CO から決めたマスロス率と 比較した。 |
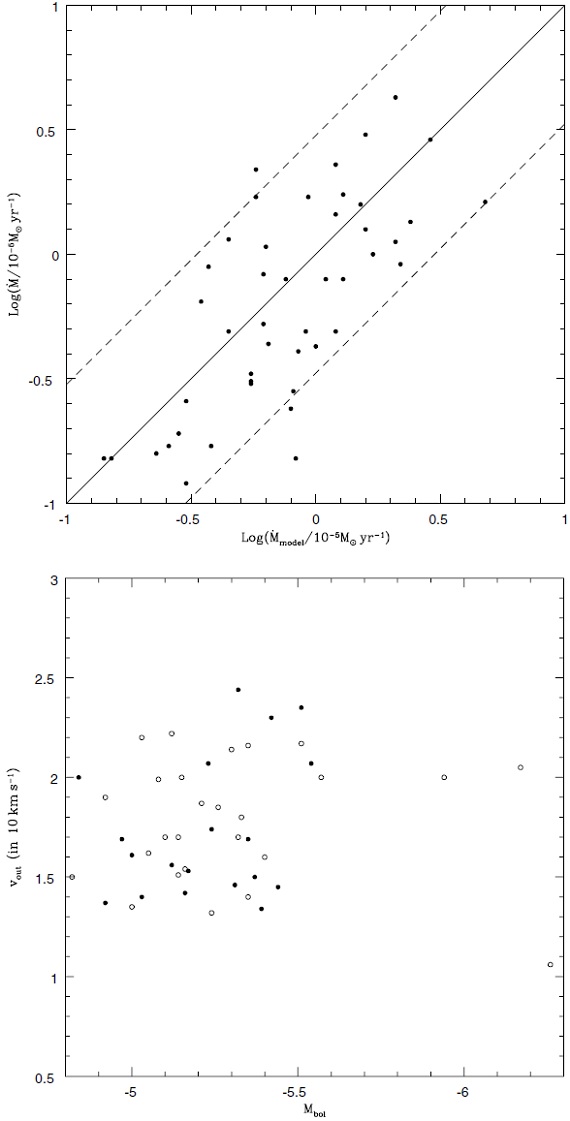 図11.上:Jura の式で決めたマスロスと Loup et al. のマスロスの比較。 下:星風速度と Mbol の関係。 |
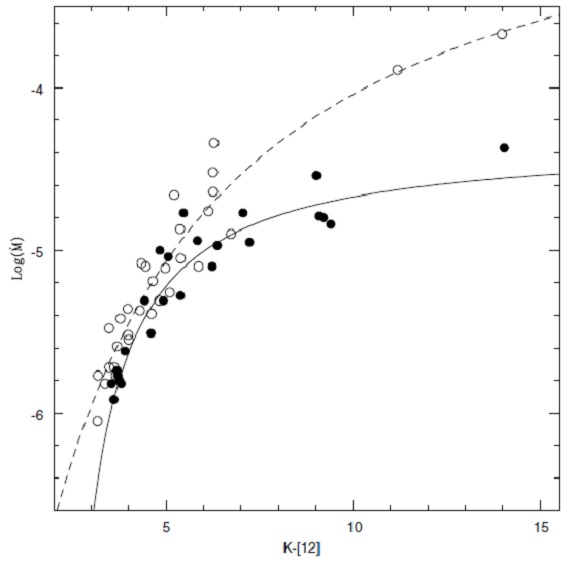 図12.dM/dt と K-[12] の関係。 図12= dM/dt と K-[12] の関係 図12にはdM/dt と K-[12] の関係を示す。この関係は Whitelock et al. 1994, Le Bertre, Winters 1998 が論じた。 図12を次の式でフィットした。 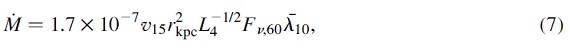 O-リッチ星で (a, b, c) = (-21.34, 3.00, -2.40), 炭素星で (-2.89, -1.79, -4.32) である。 |
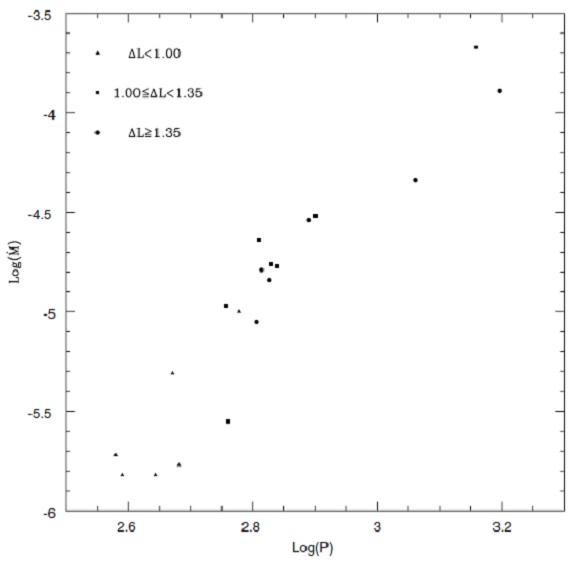 図13.dM/dt と P の関係。 図13=dM/dt と P の関係 図13には dM/dt と P の関係を示す。 平均マスロス率 後に示すが、 P > 1000 d の星は Mms が 4 Mo 以上である。 それら3星の平均マスロス率は 1.3 10-4 Mo/yr である。 P < 1000 d の星は Mms = [1, 2] Mo である。 C-リッチ星の平均マスロス率は (1.0±1.0) 10-5 Mo/yr, O-リッチ星の平均マスロス率は (2.0±1.2) 10-5 Mo/yr, である。ただし、同じオパシティと同じガス/ダスト比が使用されている。 この値の比較からはほぼ同じくらいと言う以上のことは言えない。 |
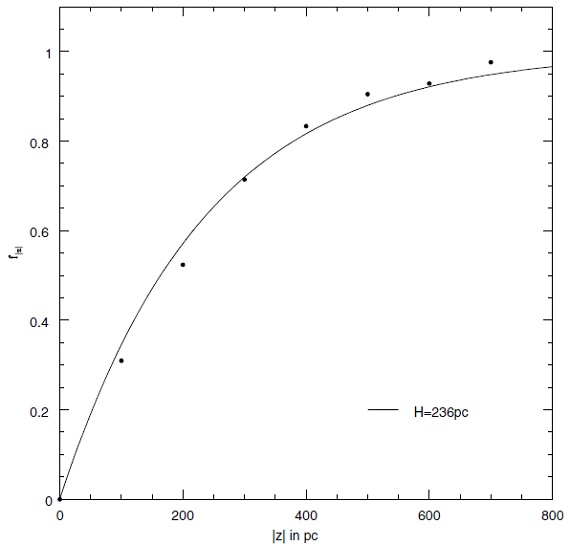 図14.関数 f|z| = |z| より内側にある星の割合。 8.1.スケール高平均 |z|星数密度の高度分布 ρ を ρ = ρo exp(-|z|/zo) と仮定する。その時、 ⟨z<⟩ = H である。対象とする空は l = [14, 230] である。 そこでの z平均から H = 235 pc が得られる。 |z| 内の割合 図14には |z| 内にある星の割合を示す。そのベストフィットから 得られる H = 236 pc で、前の結果と一致する。 8.2.前駆星質量(以下の議論はマスロス星の寿命と 主家列星質量の関係を無視しているので使えない。 ) スケール高から前駆星質量 上で求めたスケール高は前駆星質量の決定に使える。 Miller, Scalo (1979) の表1を見ると、サンプル星の初期質量は Mi = 1.2 Mo と分かる。 Mi に巾があると 別の方法として、同じ Miller, Scalo (1979) の表3=主系列星柱数密度 φ pc-2(logM)-1 を使ってみ よう。彼らの表1にはスケール高 H(Mi) が与えられている。 φ = αlogM + β とすると、α = -4.20±0.32, β = 1.20±0.14 となる。 |
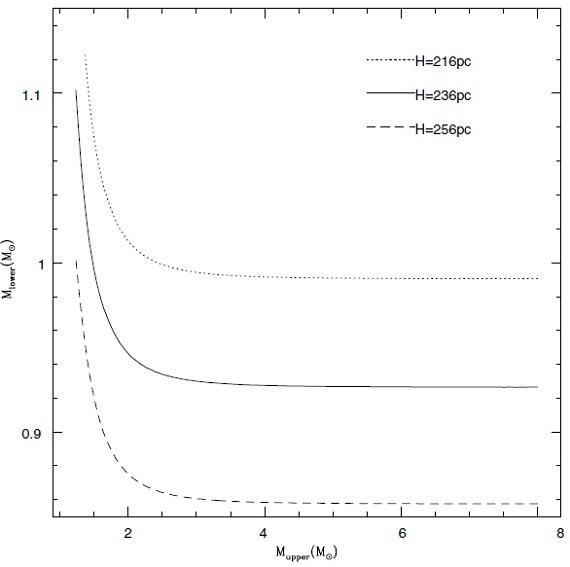 図15.異なるスケール高に対する質量上限と下限の関係。 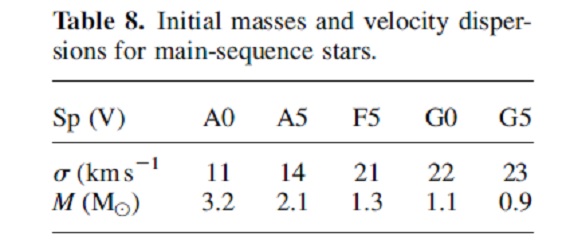 表8.スペクトル型と視線速度散布度の関係。 サンプル星の Mi の下限 = Mlower, 上限 = Mupper と仮定すると、  となり、平均 H を与えるとMlower と Mupper の関係が 図15の様に得られる。 平均質量もあわせると、 Mi = 1 - 2 Mo となる。 速度分散 P < 1000 d の星で視線速度が判っている星は 53 個 (Loup et al 1993) である。その散布度は σ = 24 ±2 km/s である。銀河回転の 補正を行うと σ = 19 ±2 km/s となる。表8を見ると、 Mi < 2 Mo と分かる。 |
8.3.表面密度求めた距離を使い、図16に銀画面上の分布を示す。大部分の星が 1.4 kpc 以内に位置する。第4象限の星が少ないのはサンプルの選択効果である。第1、 2、3象限の表面密度 σi (i = 1, 2, 3) は、σi = (Ni/(π/4) star kpc-2 で計算した。平均表面密度は σDE-AGB = (2σ1 + σ2 + σ3)/4 で計算し、σDE-AGB = 15 star kpc-2 を得た。 8.4.寿命主系列星数マスロス星の平均寿命は次式で与えられる。 τDE-AGB = (σDE-AGB/σMS) τMS σMS = (10β/αln10)( Mupperα-Mlowerα) ここに、Mupper=2, Mlower=1, α=-4,2, β=1.2 を代入する。 σMS = (15.8/4.2*2.3)=1.6. あれっ? とにかく、8.2.で使用した Miller, Scalo (1979) の主系列星表面密度関数を用いて、σMS = 2.22 star pc-2 また、同様に平均主系列寿命 τMS = 5.5 Gyr である。これらの 数字から、τDE-AGB = (3.7±1.9) 104 yr. |
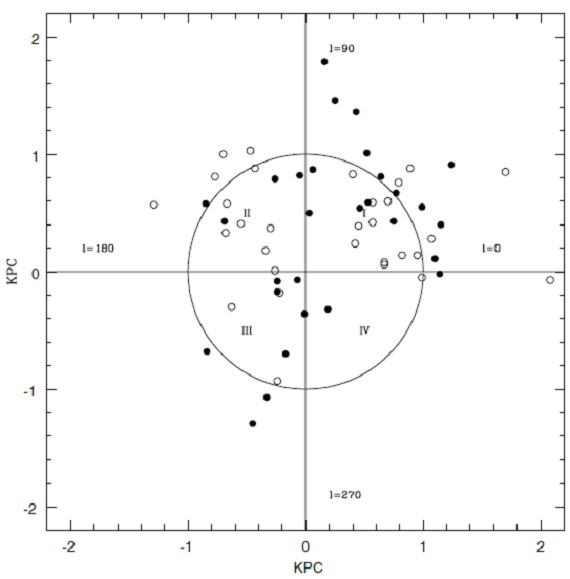 図16.銀河面上の分布。黒丸=炭素星。白丸=O-リッチ星。 |
|
熱パルス Boothroyd, Sackmann (1988) のコアマス-熱パルス間隔関係=式6を使うと、今回の低質量星サンプル では平均 Mc = 0.56 Mo, tif = 105 yr となる。 この値は DE-AGB 星の寿命τDE-AGB = (3.7±1.9) 104 yr の約2倍である。従って、 DE-AGB 期の星が熱パルスを経験するとしても 最大 1 回であろう。 |
質量還流 平均マスロス率 1.5 10-5 Mo/yr と寿命 τDE-AGB を掛けると、総マスロス Mlost = 0.5 Mo が得られる。 これは Mi-Mf 差に非常に近い。誤差は大きいが、外層質量の大部分が失われる のは高質量放出期であると思われる。また、総質量放出率は 平均マスロス率と星密度を掛けて、 (1.5 10-5 Mo/yr) (2.22 star pc-2) = 2.3 10-4 Mo kpc-2yr-1 である。 Jura, Kleinmann (1990) によると、M-超巨星からのマスロス率は (1 - 3) 10-5 Mo kpc-2yr-1 である。 従って AGB 星は星間物質への質量還流において重要な役割を担っている。 |