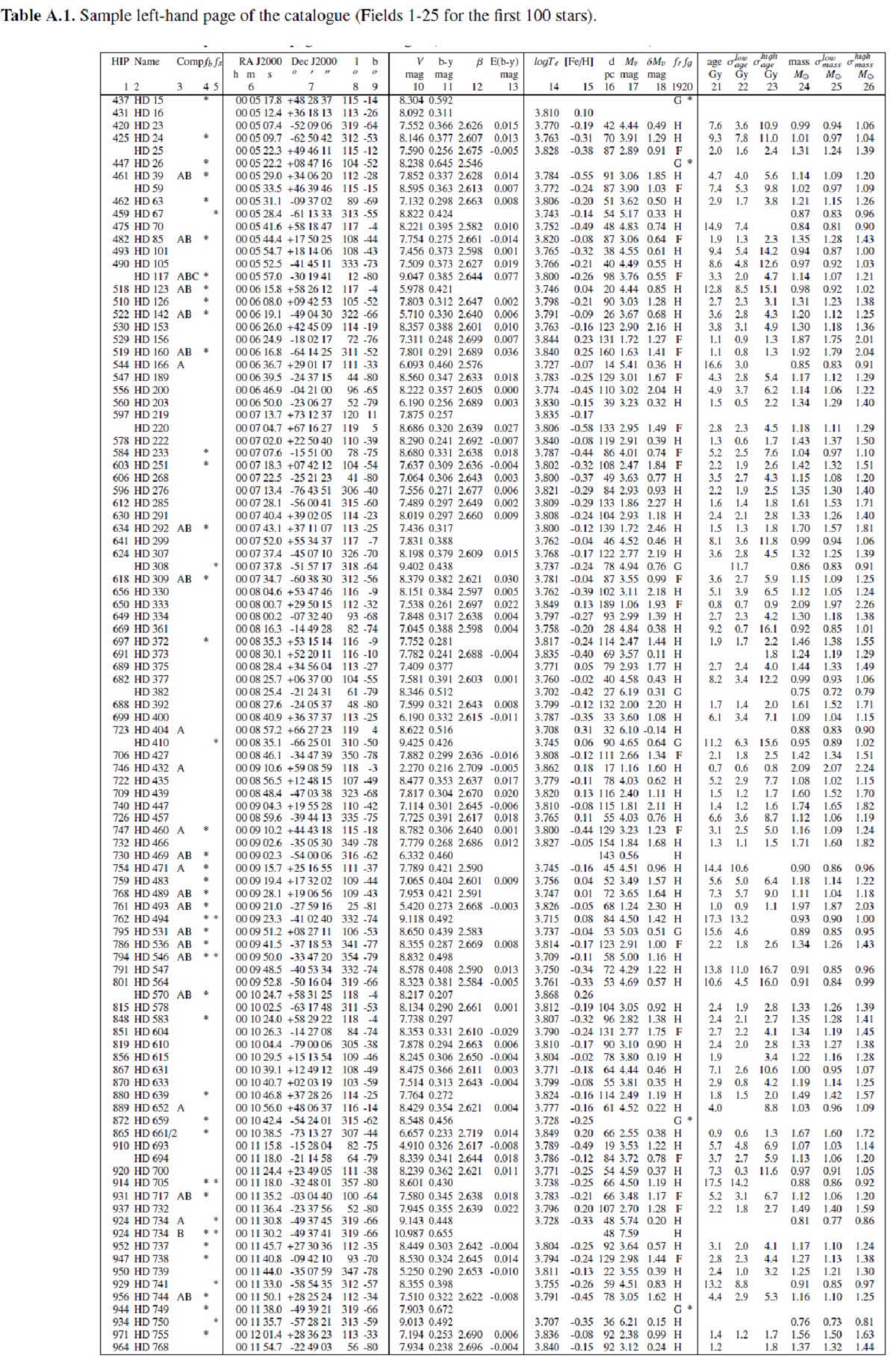
| 太陽近傍の F-, G-型矮星の等級限界完全サンプル 16,682 星のメタル量、 回転速度、年齢、運動学と銀河系内軌道を定めた。約 13,500 星に対する 63,000 回の視線速度観測から連星の大部分が検出された。それに合わせた uvbyβ 測光、ヒッパルコス視差、Tycho-2 固有運動観測から 14,139 星の運動学情報を得た。それに最近の較正を適用して有効温度とメタル量を 定めた。当時線年齢を可能な全ての星に与えた。特に統計的バイアスとエラー の評価には注意した。と言うのは通常の手法だと、それらを過小評価し、その 結果、年齢分布に偽の特徴が現れるからである。我々の結果は Edvardsson et al. 1993 と一致した。 | 太陽近傍星に対する、G 型矮星の年齢分布、年齢・メタル量、年齢・速度、 メタル量・速度関係を再調査した。まず、閉箱モデル(closed box) モデル予想 に比べ低メタル G-型矮星が欠乏している(G-dwarf 問題)ことを再確認した。 銀河中心動径方向にメタル量勾配が存在し、薄い円盤ではその形成時以来 平均メタル量の変化が少ない事、全ての年齢でメタル量の分散が大きいこと、 渦状腕と分子雲により薄い円盤の運動学的加熱が連続的に起きていることが 判った。空間運動の V 成分に見られる特徴は年齢とメタル量にわたって広が っている。これは渦状腕のストカスティックな効果で、古典的な運動群に 対応しない。さらにこれは厚い円盤の星を運動学的基準で見分けることを 面倒にする。 |


|
F-, G-矮星 F-, G-矮星の視差、固有運動が得られるようになったが視線速度データ が不完全であった。この研究ではその欠落を補った。重要なことは 繰り返し観測の結果連星が同定されたことである。13500 星に対し、 63000 回の観測が行われた。 |
物理パラメター 天体物理的なパラメタ― Teff, Mv, [Fe/H] も再較正されて与えられた。 それらの例を表1A に示す。 |
|
HD カタログ 全天から 40 pc 内の F-, G-矮星を完全に選び出したい。その為 に HD カタログを利用する。このカタログは A5-G0 星で mvis < 8.3 G0 星は mvis = [8.3, 8.40] G5 と只の G 星は mvis < 8.6 を全て採用。 A5 型は十分に早期なので、とても低メタルな F 型星でも含まれる。 ("とても低メタルな"F-型星が 誤って A 型とされていても掬い取る? ) 一方、HD カタログ中の K0 星は大部分巨星であり、それらの距離、光度、 接線速度、年齢の信頼できる決定は難しい。 ミシガン分光カタログ 古い高メタル矮星をサンプルに含めることは 「G-矮星問題」を再検討 する際の観測的基盤の準備に望ましい。しかし、多数の HD K-巨星を観測 することはそのような星の同定には非効率である。 (低メタルF−星と逆の状況? ) そこで、ミシガンスペクトルカタログから δ < -26° の 1227 G0V - K2V 星を加えた。それらは以前に観測されたことがなく、 スペクトル型から推定されたもので、 mpg から」 50 pc 以内 にいると考えられる。それらは距離からは 40 pc 全体を含むが全天の 28 % しかカバーしない。 2.1.測光サーベイほぼ全てを uvbyβ 測光した。それに既知の観測も合わせ、 総合 FG カタログには 30465 星が載った。2.2.サンプル星の定義基準 次の4つの内どれかに当てはまる星を選ぶ (i)Crawford 1975 と Olsen 1985 の F-型星較正が当てはまる。 (ii)β がない。 0.240 < b-y ≤ 0.460, [m (iii)0.205 < b-y ≤ 0.240, [m (iv)Olsen 1984 の G-, K-型星較正が当てはまる。 |
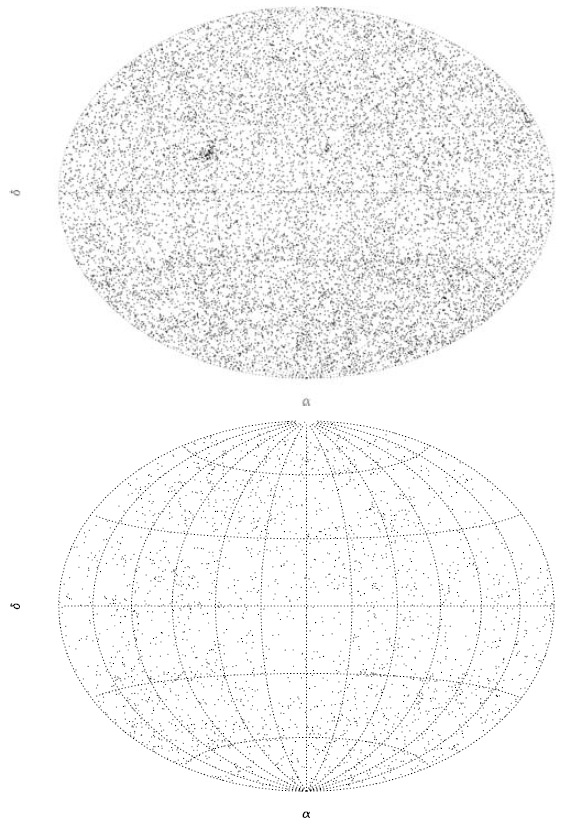 図1.上:視線速度を観測した 14,139 星の分布。ヒアデス星団と δ=-26° より南での密度超過に注意。 下:観測されていない 2543 星の分布。 基準の役割 基準 (iii) は F-型星の熱い辺りで低メタル星が F-型から落ちないことを 保証する。基準 (ii) と(iii) は β の代わりをさせている。 基準 (i) と(iv) と V < 9.600 は較正目的で観測した暗い星も含める。 リストに 16,682 星が残った。 分布 図1にそれらの分布を示す。較正のために丁寧な観測が行われた ヒアデス星団方向とミシガンカタログから晩期型のサンプル星の補充が あった δ -26° で密度超過が見られる。 |
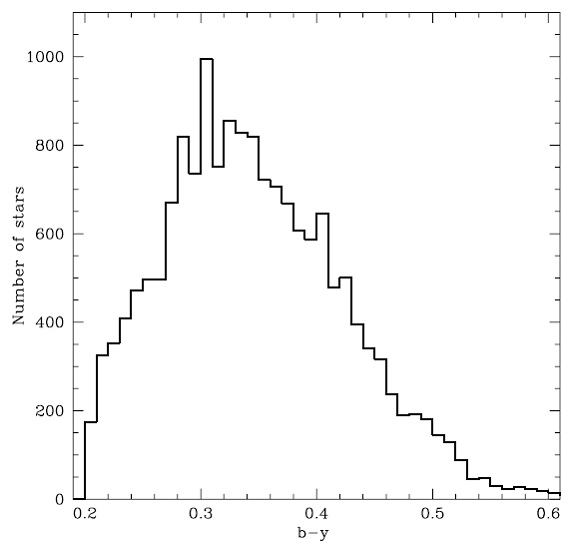 図2.b-y カラーの分布 3.1.ストロームグレン uvbyβ 測光3.2.視線速度3.2.1.CORAVEL 観測3.2.2. CfA 観測3.2.3. 文献データ3.2.4. 変動基準と連星の検出 |
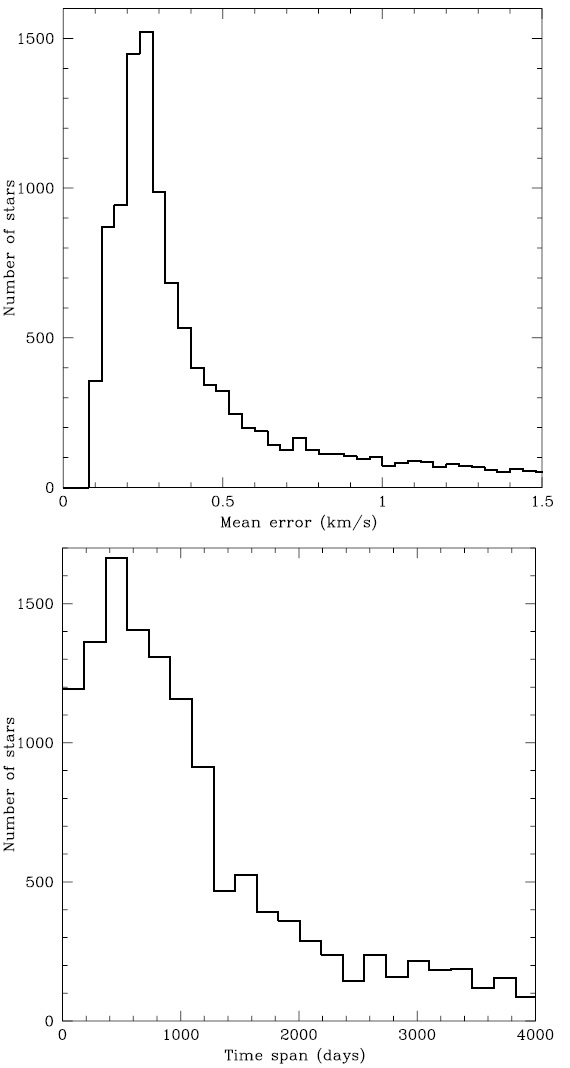 図3.上:平均視線速度のエラー分布。下:観測期間の分布 |
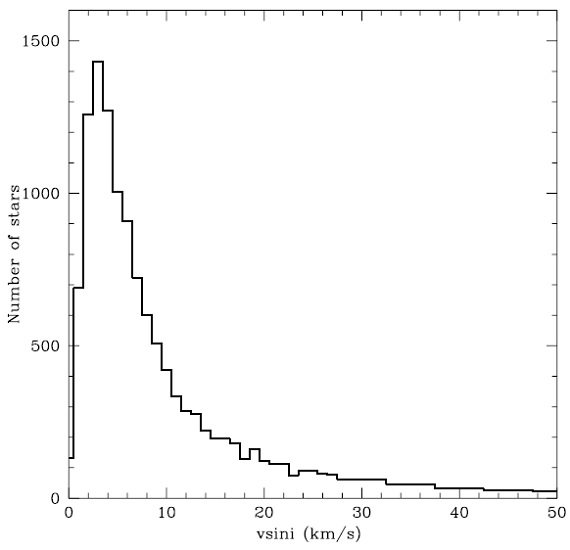 図4.回転速度の分布 3.3.回転速度3.4.視差3.5.固有運動 |
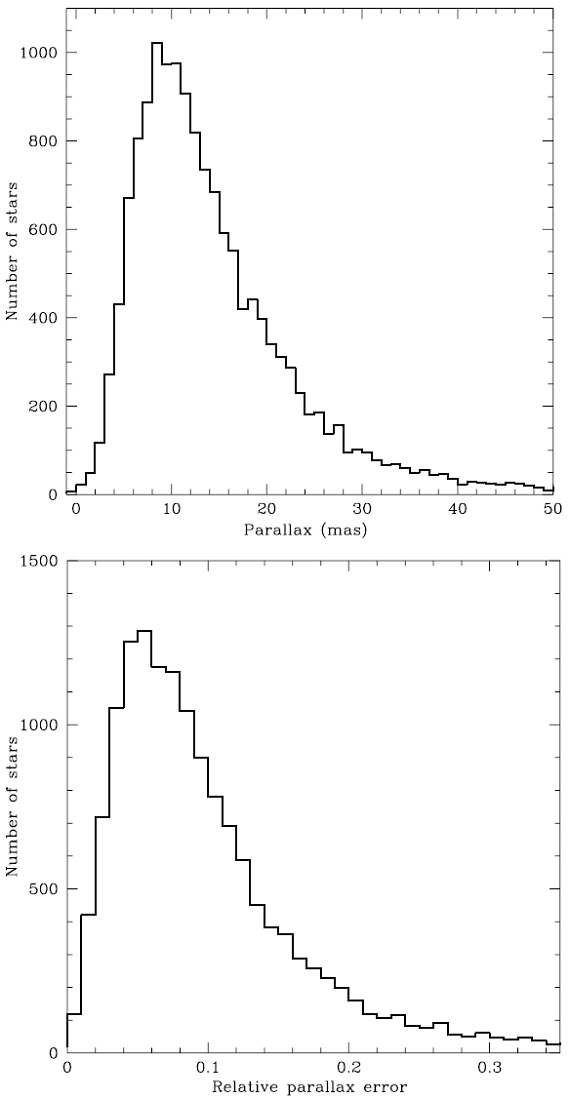 図5.上:ヒッパルコス視差の分布。下:視差エラーの分布 |
4.1.星間赤化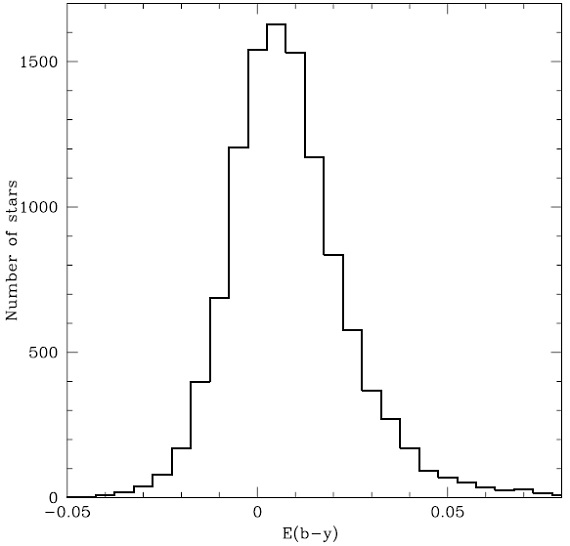 図6.赤化の分布 |
4.2.有効温度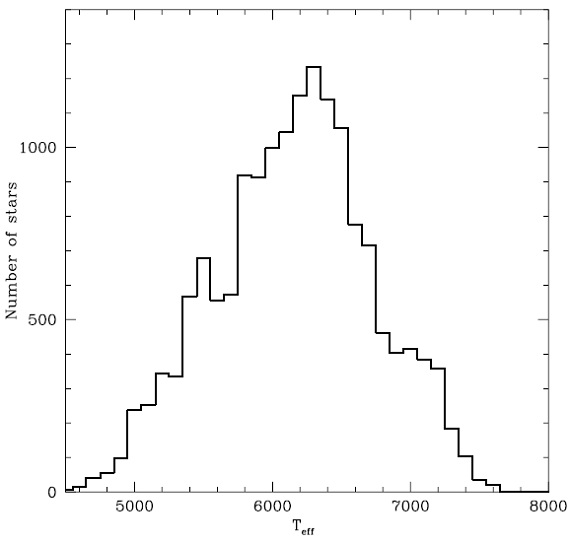 図7.有効温度 Teff の分布 |
4.3.メタル量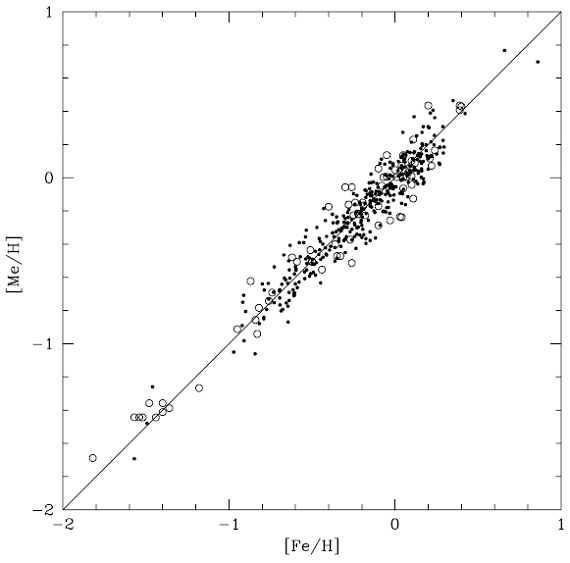 図8.較正に使った星の測光メタル量と分光メタル量の比較、白丸 = G, K 型星。黒点= F 型星 |
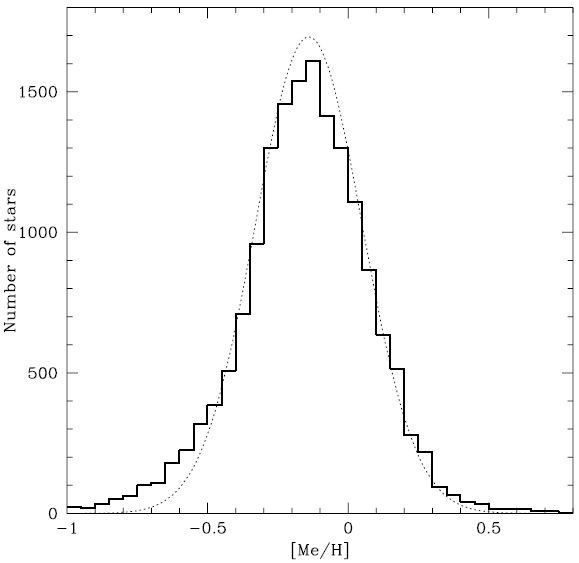 図9.実線=全サンプル星のメタル量分布。点線=ガウスフィット。 平均 -0.14, 散布度= 0.19 dex. |
4.4.距離と絶対等級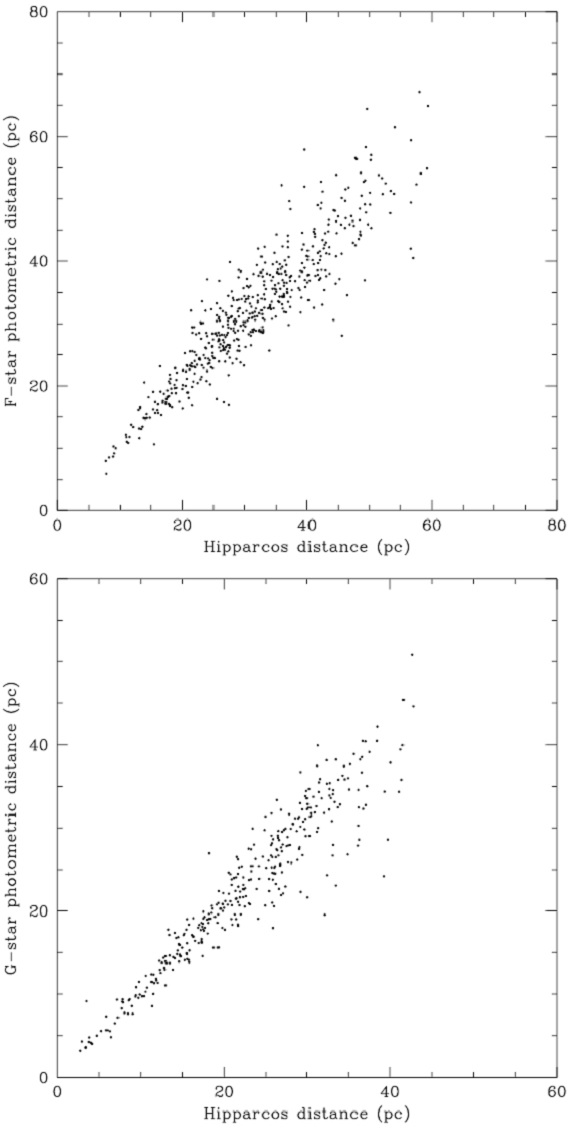 図10.測光距離とエラー 3 % 以下のヒッパルコス距離の比較。 上: F 型矮星。下: G 型矮星。 距離の不定性 図10から測光距離の不定性は約 13 % である。そこで、ヒッパルコス 距離のエラーが 13 % 以下の場合はそちらを使用することにした。 |
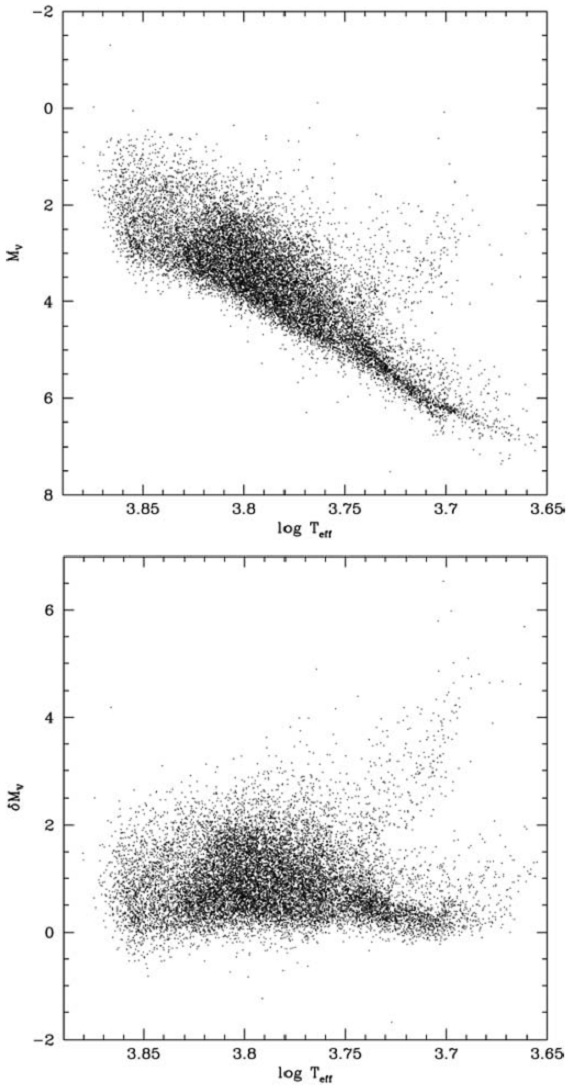 図11.上:Mv と, 下:δMv の Teff に対する関係。サンプル星は F-, G-型矮星。 絶対等級 採用した距離と見かけ等級から絶対等級を計算した。 (測光距離は絶対光度から求めるの では?その場合単に仮定した値が得られるだけではないか? ) δMv δMv = 星の観測 Mv と、同じカラー、メタル量を持つ ZAMS Mv との 差で、進化の低度を示すと見做される。 |
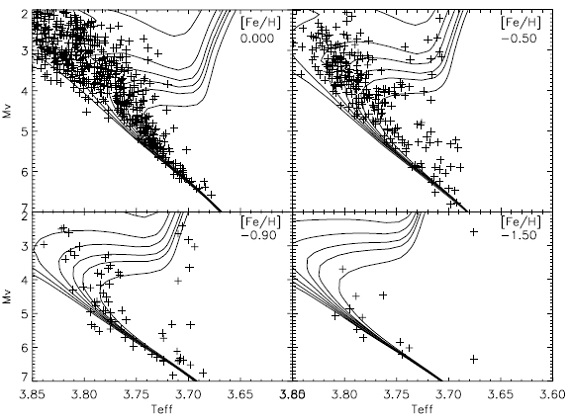 図12.メタル量で分けた HR 図上のサンプル星とパドヴァ等時線。 [Fe/H] は 左上=[-0.02, 0.02], 右上=[-0.45, -0.55], 左下=[-0.70, -1.10], 右下=[-1.25, -1.75]. α 過重と温度補正適用。 4.5.1.進化モデルの選択4.5.2.モデル組成の選択 |
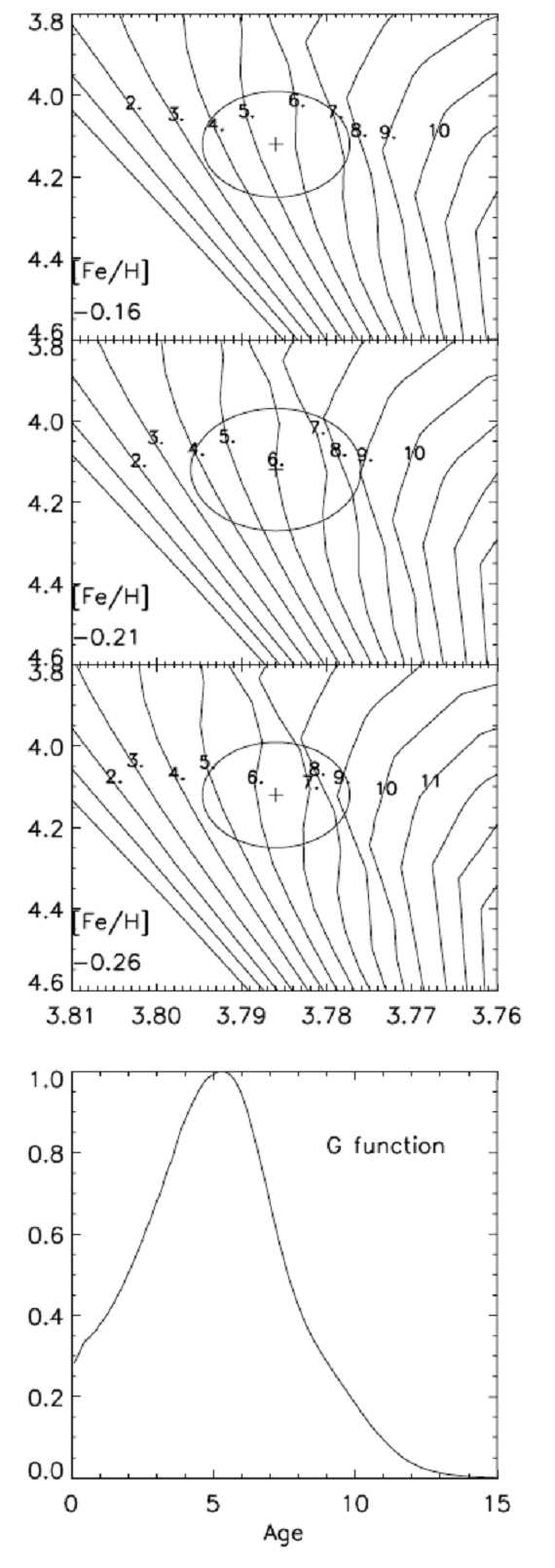 図13.上の三つ: HR キューブの3枚の切断面。中央パネルは観測点を、 それに 1-σ エラー楕円を通る3枚の切断面。下:等時線上の全ての点 を使った確率関数。 |
4.5.3.温度スケールの調整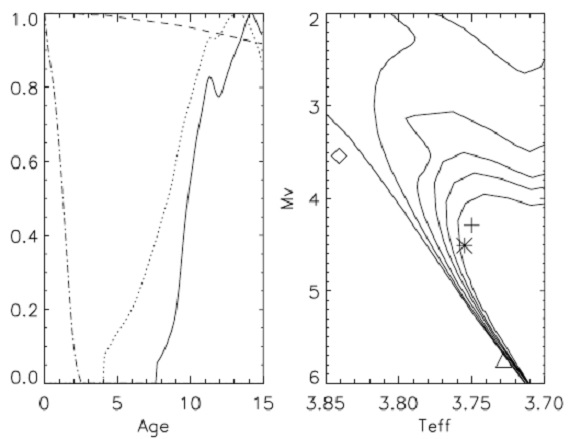 図14.右:年齢決定が怪しい HR 図上の領域にある星。左:対応する 確率分布。十字=実線、アステリスク=点線、三角=破線、菱形=一点破線 に対応。 |
4.5.4.年齢決定における統計的バイアス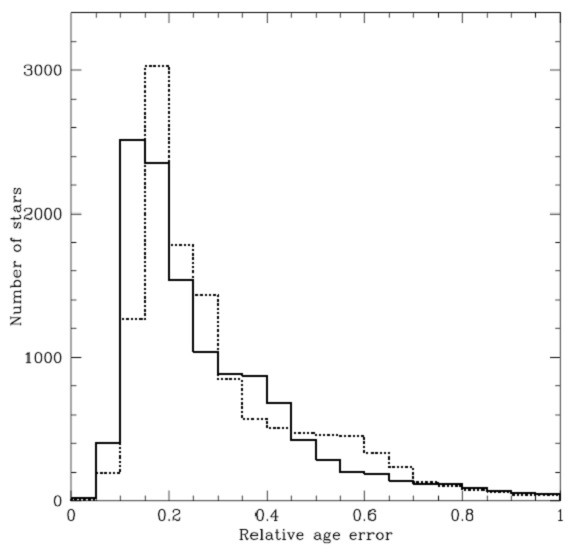 図15.カタログの年齢エラーの 1-σ 上限=点線、下限=実線ヒストグラム。 |
4.5.6.年齢エラーの推定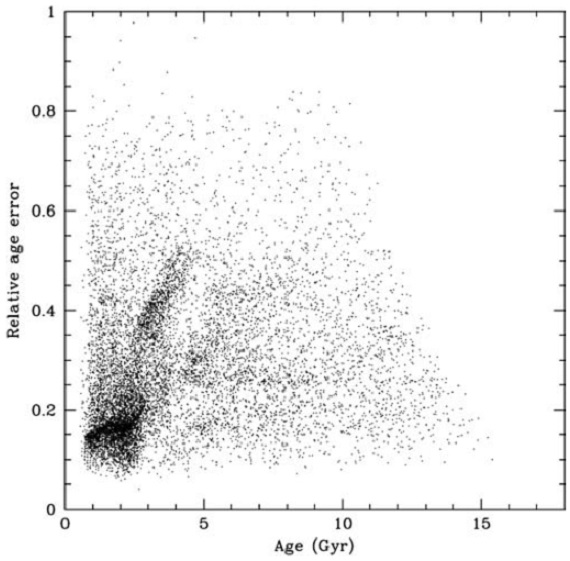 図16.年齢の相対誤差(下限と上限の平均)と年齢の関係。 |
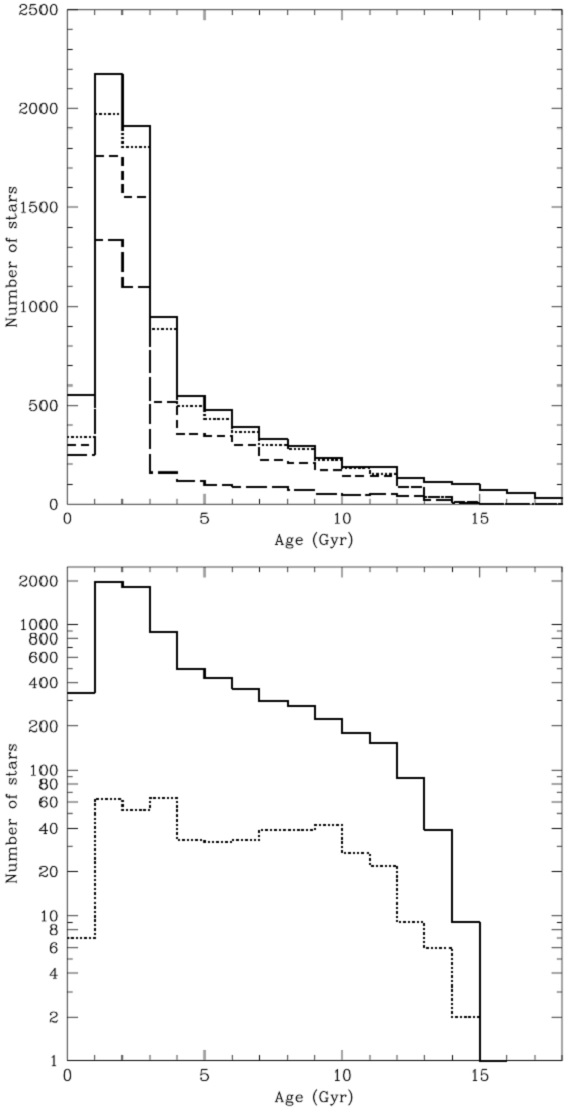 図17.上:年齢分布。実線=全サンプル。点線=年齢誤差の小さい星。 短破線=エラー 50 % 以下の星。長破線=エラー 25 % 以下の星。 下:実線=等級限界サンプル中の年齢が良く決まった星。点線= 40 pc 内の体積限界サンプル中の距離エラーが小さい星。 精度に対する要求がきつくなるにつれ古い星が消えて行くことに注意。 |
4.5.7.結果のチェック |
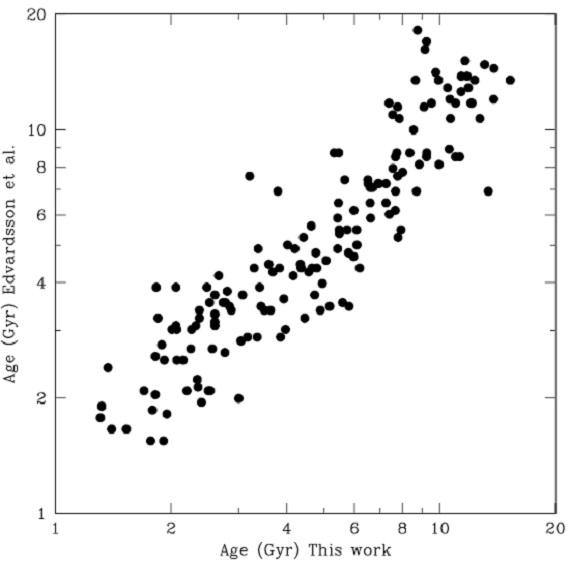 図18.Edvardsson et al 1993 の年齢との比較。 |
4.6.星質量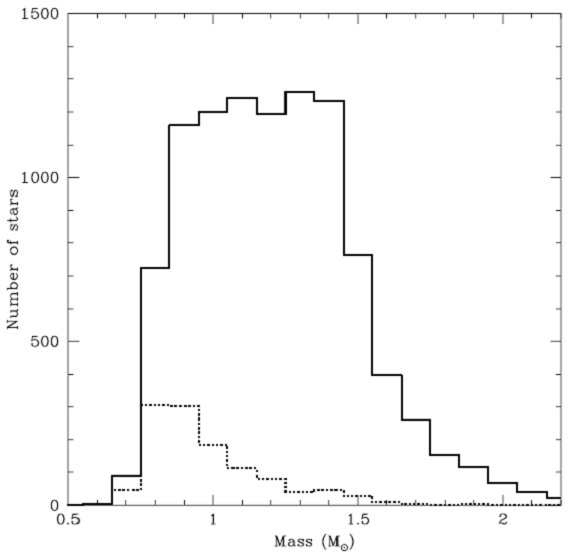 図19.サンプル星の質量分布。実線=全サンプル。点線= 40 pc 以内の星。 |
4.7.空間速度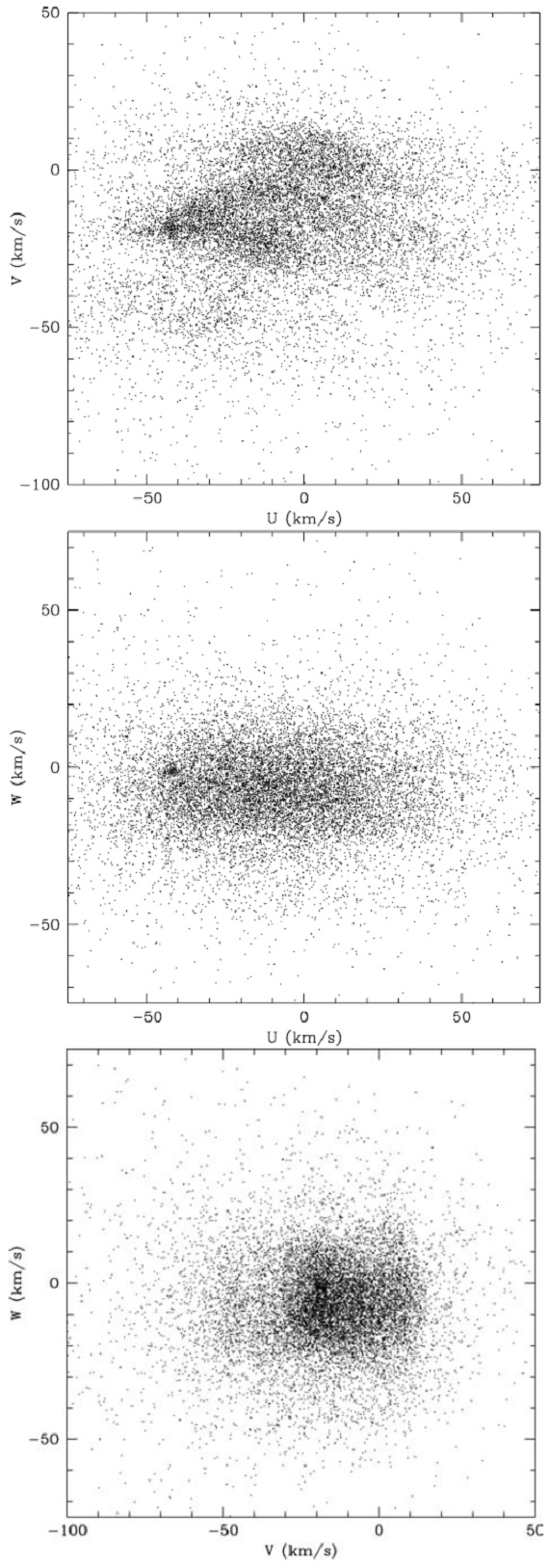 図20.全サンプルの速度分布。 |
4.8.銀河系内軌道 |
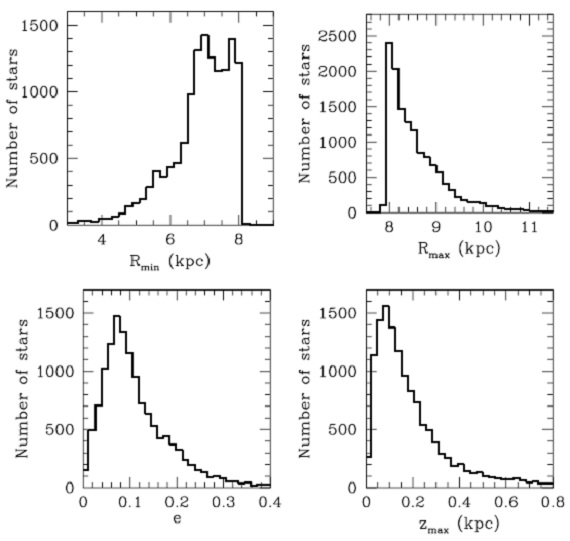 図21.円盤内軌道のキーパラメターの分布。 |
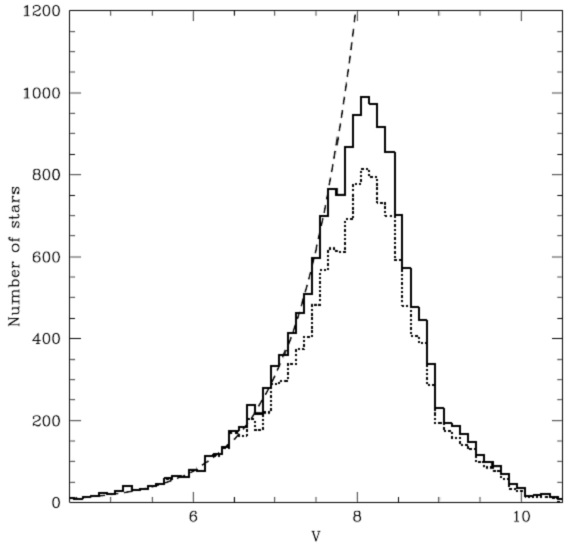 図22.観測 V 等級の分布。実線=全サンプル。点線=視線速度測定アリ。 破線=一様で体積制限サンプルに予想される分布。 5.1.連星5.2.等級完全性5.3.体積完全性5.4.質量完全性5.5.年齢完全性 |
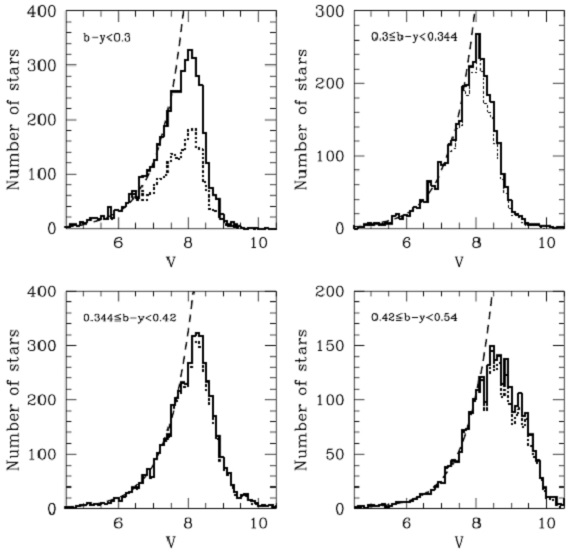 図23.b-y カラー別の V 等級分布。 実線=全サンプル。点線=視線速度測定アリ。 破線=一様で体積制限サンプルに予想される分布。 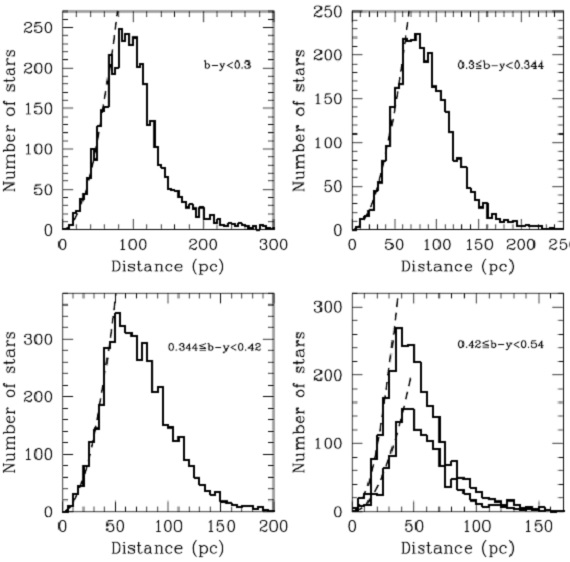 図24.b-y カラー別の 距離分布。 破線=一様で体積制限サンプルに予想される分布。 右下の下側線= δ -26° より南の星。 |
6.1.メタル量分布 (G 型矮星問題)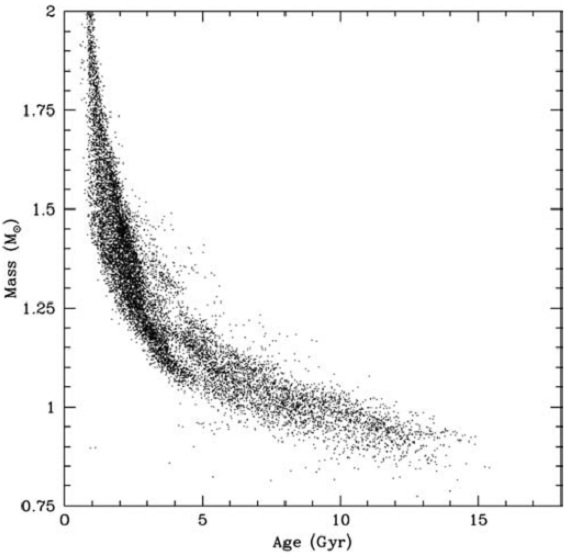 図25.「良く決まった」年齢の星に関し、年齢と質量の関係を示す。 年齢と質量の見掛けの相関は進化した星による強調された効果と 進化していない星では信頼できる年齢が得にくいことによる。 |
6.2.年齢 - メタル量関係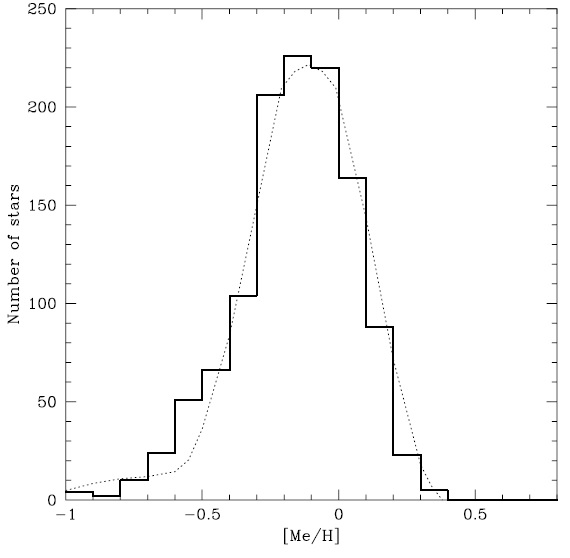 図26.実線=体積完全サンプルのメタル量分布。 点線= Jorgensen2000 の G 矮星再構築分布。 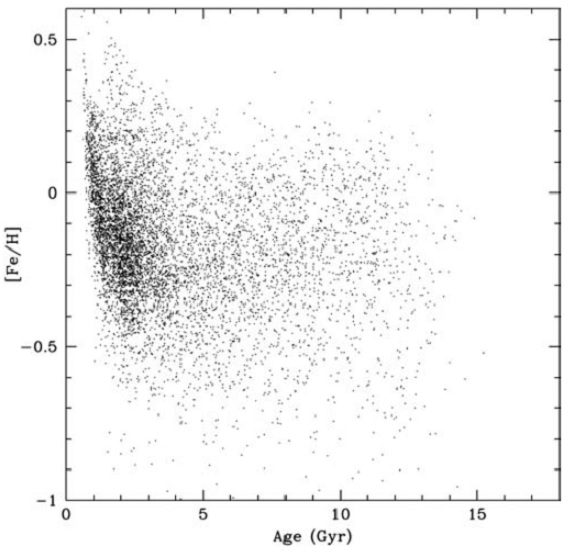 図27.等級限界サンプル中の「良く決まった」年齢の 7566 星の年齢 - メ タル量関係。個々の星の年齢エラーは 50 % を超す。 |
6.3.円盤におけるメタル量の動径に沿った勾配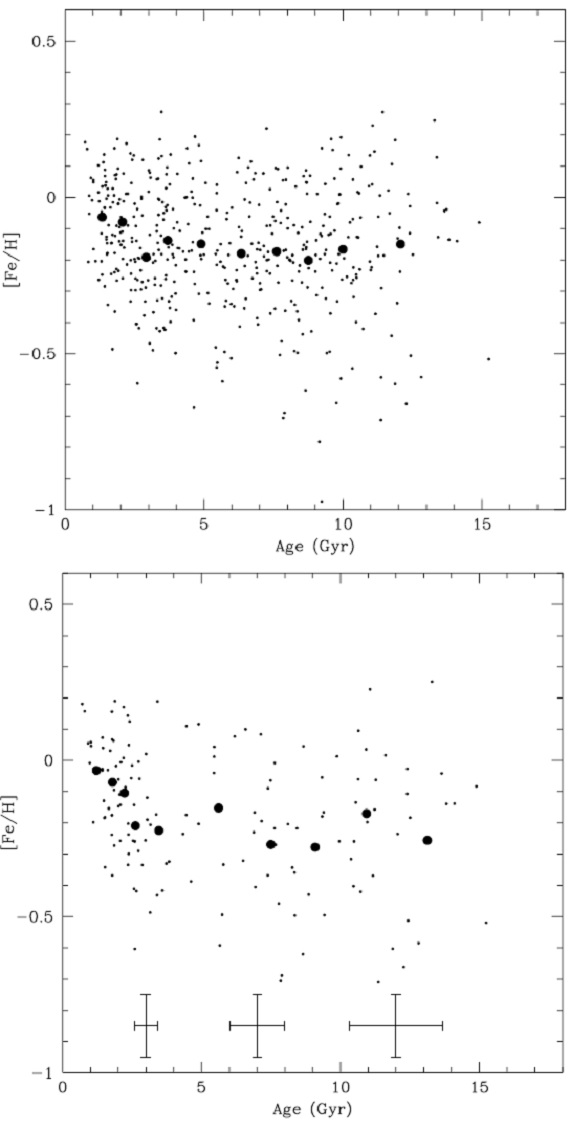 図28.年齢-メタル量関係。サンプルは 40 pc 以内、大きい黒丸=平均。 上:「良く決まった」年齢の 462 星。下:年齢エラー 25 % 以下の 142 星。 |
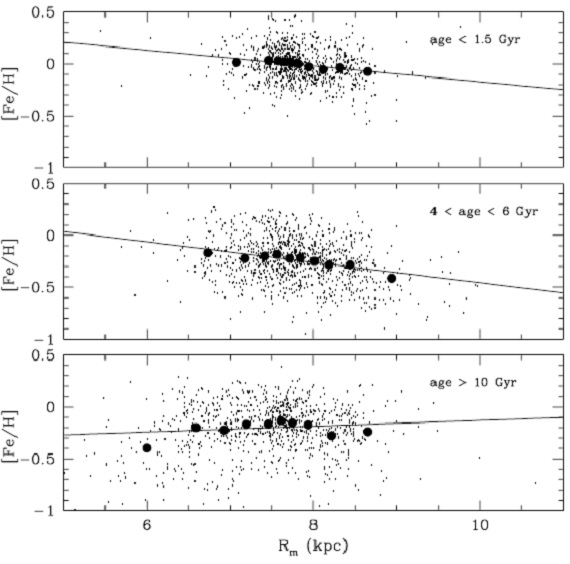 図29.動径に沿ったメタル量の勾配。Rm = 軌道の平均半径。 |
6.4.年齢・速度関係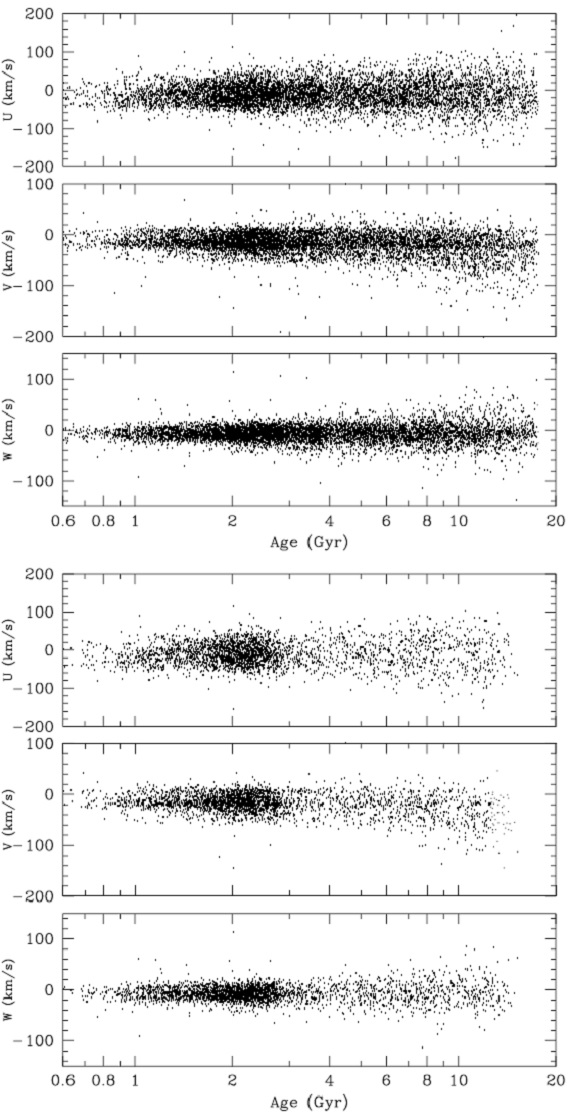 図30.U, V, W と年齢の関係。上側:年齢が「良く決まった」7237 星。 下側:年齢エラー 25 % 以下の星。 |
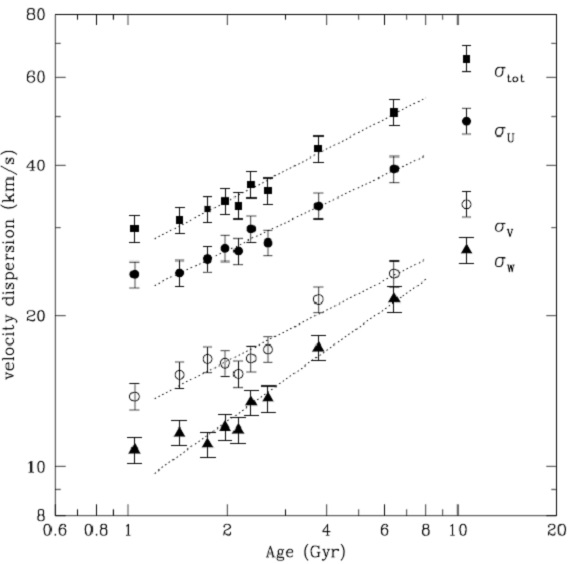 図31.年齢エラー 25 % 以下のサンプル星の U, V, W 散布度と年齢の関係。 点線=フィットの際、最も古い年齢グループ(厚い円盤星混入)と最も若い 年齢グループ(運動が緩和していない)は外した。 |
6.5.メタル量・速度関係 |
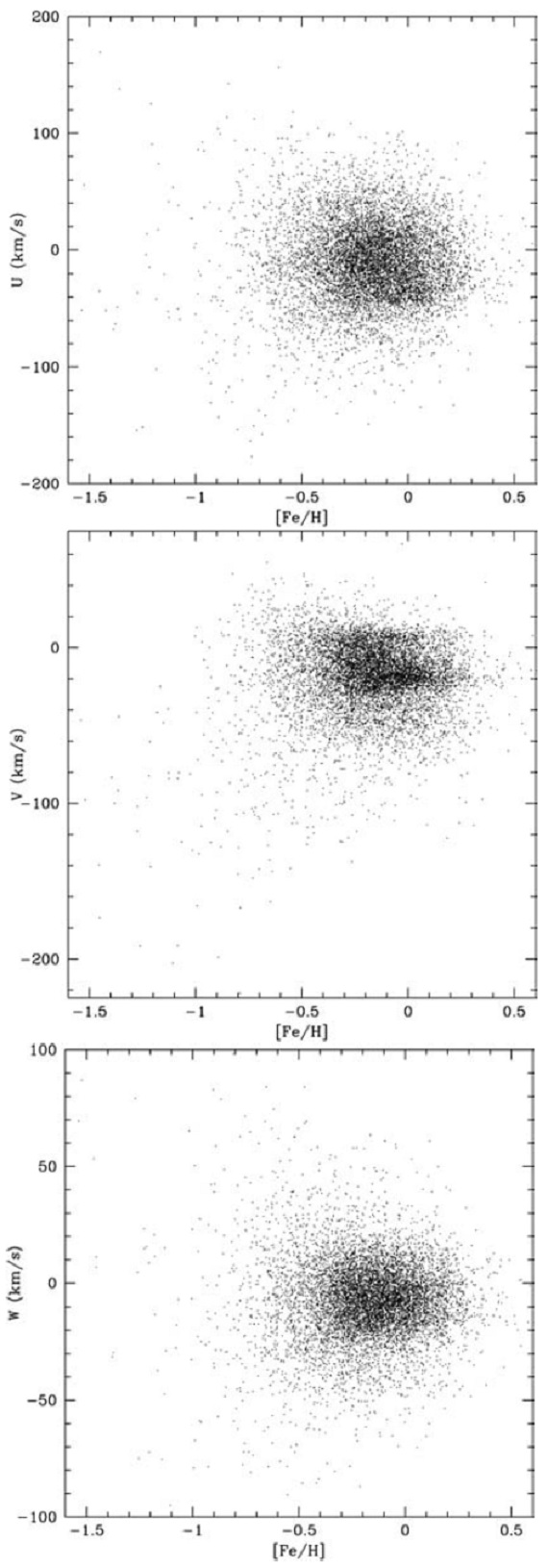 図32.U, V, W とメタル量の関係 |
|
年齢-メタル量関係 図27、28の年齢-メタル量関係は、閉箱モデルまたは一意な関係が銀河 円盤の進化に十分であるという考えに終止符を打った。薄い円盤の全期間を 通じて低メタルと高メタルの星が並存することを許すモデルが必要である。 (ある時期に様々なメタル量の分子雲が 存在するということ?それともメタル勾配があるガスから生まれ後で動径混合? ) |
年齢-速度関係 今回の新しい年齢-速度関係は力学的加熱のモデルに強い拘束を掛ける。 また、それは星団の生き残り率にとっても重要である。また、バーの力学効果 の検出に繋がるかも知れない。 |

|
|
|

|
|
|

|
|
|

|
|
|
