Galactic Structure towards the North Galactic Pole Based on an Analysis of UBV Star Count Data


Yoshii, Y., Ishida, Stobie
1980 AJ 92, 323 -



　アブストラクト

　ＮＧＰ方向の星計数　

　NGP 方向 21.46 deg2 V = 19 より明るい 18,000 星の UBV スター カウントを報告する。メタル量グループ毎に光度関数、色等級関係、二色関係 を適用して、円盤と楕円体成分の間にあるかもしれない中間種族に対して最も 厳しい制限を与える銀河系モデルを構築した。モデルパラメター間の結合を 考え、モデルの決定には最小二乗法を用いた。 		　中間種族はあった　

　モデルから規格値 2 % で、スケール高 1 kpc の中間種族の存在が明らかと なった。この成分は V = 15 - 17 では約 20 % を占めている。メタル勾配は d[Fe/H]/dx = -0.5 ±0.1 kpc-1 (z ≤ 2 kpc) である。


　１．イントロ　

　B&S モデル　

　B&S モデル Bahcall, Soneira 1980b は円盤と楕円体の２成分に同じ太陽近傍光度関数を適用している。 円盤はスケール高 325 pc 指数関数密度則に従い、楕円体はドボークルー型 r1/4 則, 有効スケール高 5 kpc、に従っている。楕円体規格値は 0.00125 Schmidt 1975 である。双峰性カラー分布のピークは夫々が円盤と楕円体によるものと された。 Bahcall, Soneira 1984 では銀河系 5 方向の V ≤ 22 星計数データがこの 2 成分モデルでフィット できることを示した。

　吉井 1982 で厚い円盤を検出していた！　

　興味深いことに、 V = 18 等までのデータから中間種族が必要かどうかを 判定できるのである。 Yoshii 1982 は銀極方向方向 G ≥ 19 の Basel SA 57 データを解析し、円盤と別の 第２成分 　（彼の言い方では「ハロー成分」）　 を分離した。この第２成分の光度関数には球状星団のそれを採用し、巨星の 存在も考慮した。そのスケール高は 2 koc で、規格値は 1 - 2 % である。

　厚い円盤　

　 Gilmore, Reid 1983 は南銀極 I ≥ 18 の星計測に測光視差を適用した。彼らは全ての星が主系列星 であると仮定した。こうして彼らもまたスケール高 1.45 koc, 規格値 2 % の 第２成分を見出した。彼らはそれを「厚い円盤」と名付けた。この命名は Burstein 1979 が横向き S0 銀河の第２成分に付けたことに倣っている。 		　Bahcall の批判、Gilmore の統合案　

　 Bahcall, Soneira 1984 は円盤と中間成分のみでは V ≥ 20 のカラー分布を説明できないことを示した。 この批判を取り入れて 　 Gilmore 1984 は３成分銀河モデルを提案した。Bahcall et al 1985 は G ≤ 19 の バーゼル星計数 は B&S ２成分モデル（1980, 1984）、Gilmore 1984 ３成分モデルと合うことを 示した。 （ G ≤ 19 なら円盤＋中間成分で B&S では カバーしきれないんじゃなかったのか？）

　低メタルの効果　

　V = 16 - 18 での B-V, U-B カラー分布は銀河モデルにより厳しい制約を 与える。この等級帯では中間種族の比率が高いからである。 同じ B-V カラーに対し低メタル矮星は暗く、低メタル巨星は明るくなる。 従って、測光距離はメタル量に大きく影響される。低メタル星は円盤から 遠くまで拡がっている Sandage 1980, Yoshii 1984 ので、円盤から遠い 星の分布はメタル量分布と合わせて解く必要がある。

　メタル量と紫外超過との関係　

　メタル量と紫外超過との関係は分光観測による較正の結果、高い精度で 知られている。[Fe/H] = 0 から -2 への変化の結果、ターンオフでは Δ(B-V) ∼ 0.1, Δ(U-B) ∼ 0.3 が生じる。(U-B) の 大きな変化はブランケッティング効果によるもので、実際 (U-B) 分布は メタル量決定に有用な道具である。
　銀極方向は円盤から垂直な分布を調べるに最適である。そこで新しい UBV データ を使って　Yoshii 1982 の方法をさらに発展させたい。


　２．観測と測定　

　木曽観測所で行われた U 6枚, B 5 枚, V 5 枚の 乾板を COSMOS で測定した。 等級は Purgathofer 1969, Chiu 1980 光電測光を標準に較正した。較正結果を 外挿することはしなかったので、V = 19 より暗い星は捨てた。 V = 19 まで で B - V もある星は 18,000 個であった。 　V = 18 より明るい等級では平均等級のエラーは 0.04 等である。それより 暗いと星と銀河の分離が完全でないので使用しない。星計数データは 第４章 (f) に述べるように銀河モデルの結果と並べて示す。データの詳細は Stobie,Ishida 1987 に述べられている。


　３．データ　

　星計測の基本式　

　星計測の基本式は、

　　　　　　　A(V) = ω Σi,j∫z φ j,z(Mv) Di(z) z2dz　　　　(1)

　　　　　　　V - Mv = 5 log z - 5 + av(z)　　　　　　　　　　(2)

ここに、 i = 1 (円盤), 2 (中間), 3 (楕円体) で、 j = 1 (主系列), 2 (巨星) を指し、 φj,z(Mv) は 高度 z での 1 pc3 内での Mv = Mv -１/2 から Mv + 1/2 内の j = 1 (主系列), 2 (巨星) 星の数。 Di(z) は z = 0 pc で 1 に規格化した各成分の密度。 av(z)は無視する。

式(1)は i と j で積分結果を足している。したがって、n(i,j,z,Mv) = φj,z(Mv) Di(z)　は、i-種族で、j-クラスの星の単位体積、 単位見かけ等級当たりの星数である。Di(z)　の上の定義は間違って いる。
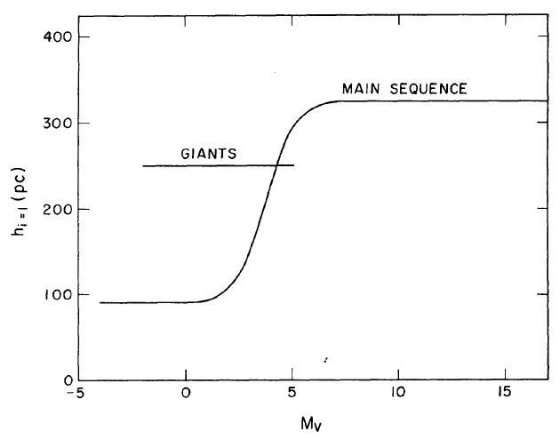
Di(z) は各種族(i = 1, 2, 3)の数密度 ni(z) を円盤 星の銀河面での値で割ったものである。つまり、 Di(z) ≡ ni(z)/n1(z=0)

　すると、φj,z(Mv) は、 i-種族に対する光度関数、 Mv で積分した総数(j=1 + j=2) は z = 0 での円盤星数密度に規格化、を主系列 (j=1) と 巨星(j=2)とに分割したものである。だから本当は φi,j,z(Mv) と書くべきなのである。

　色・等級関係　

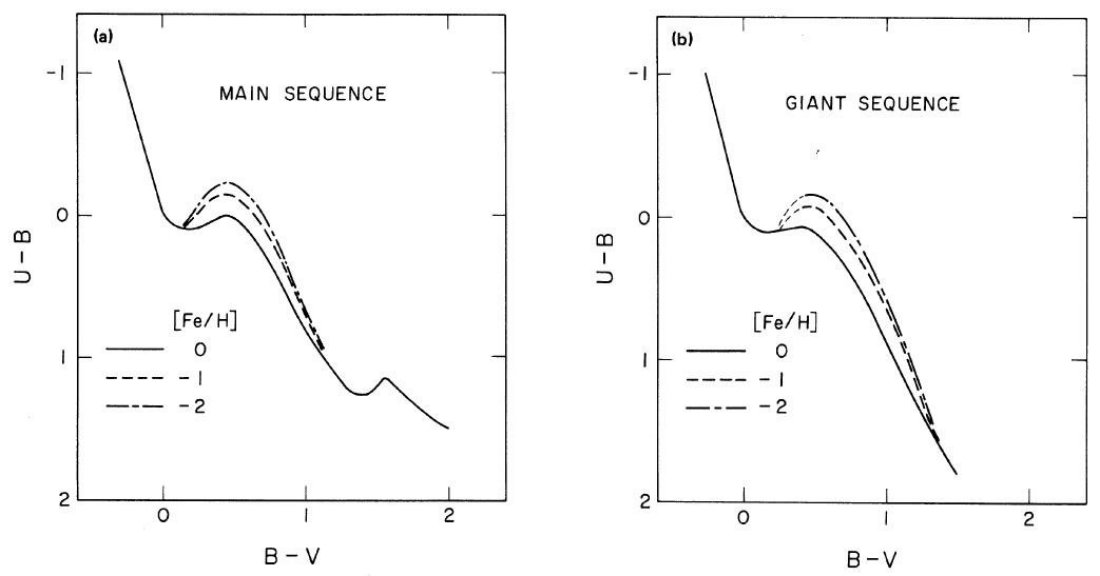
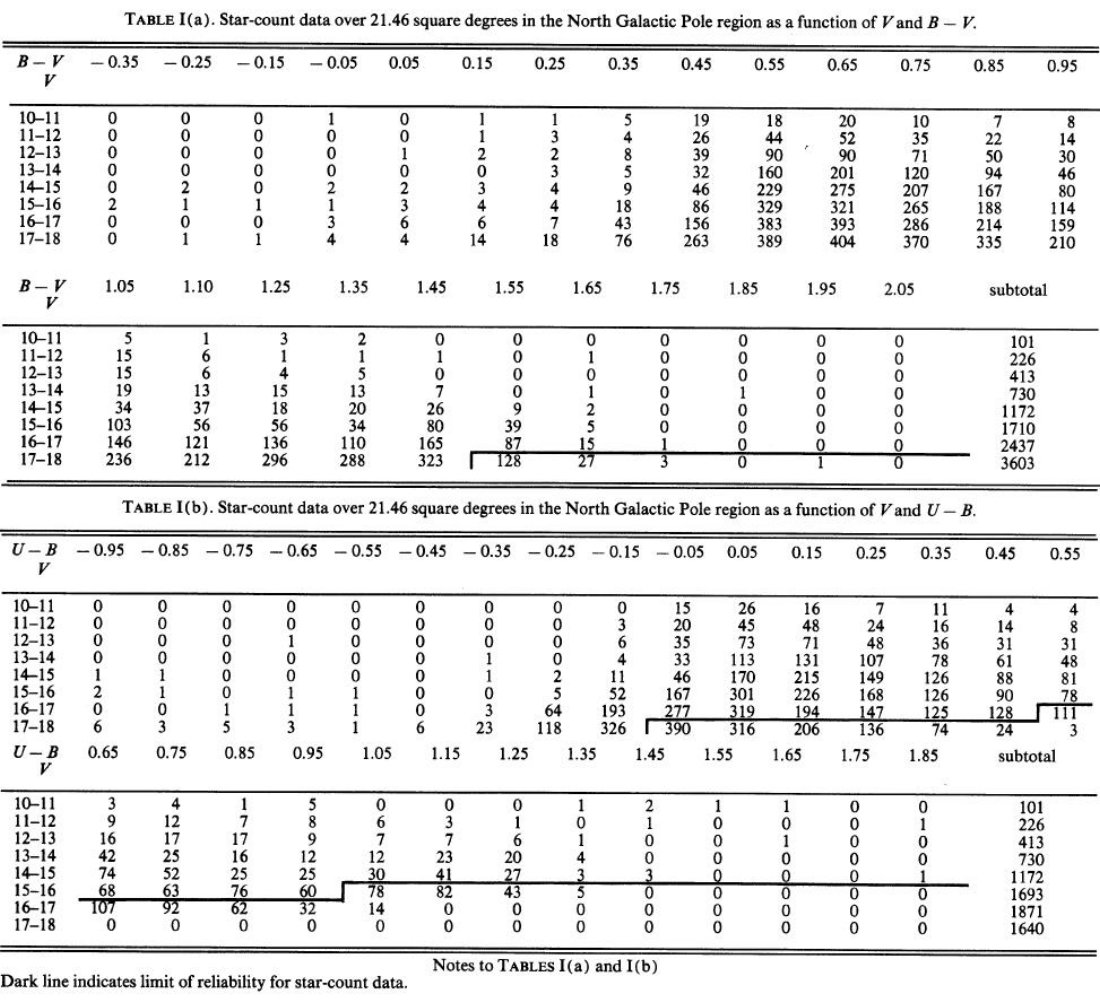
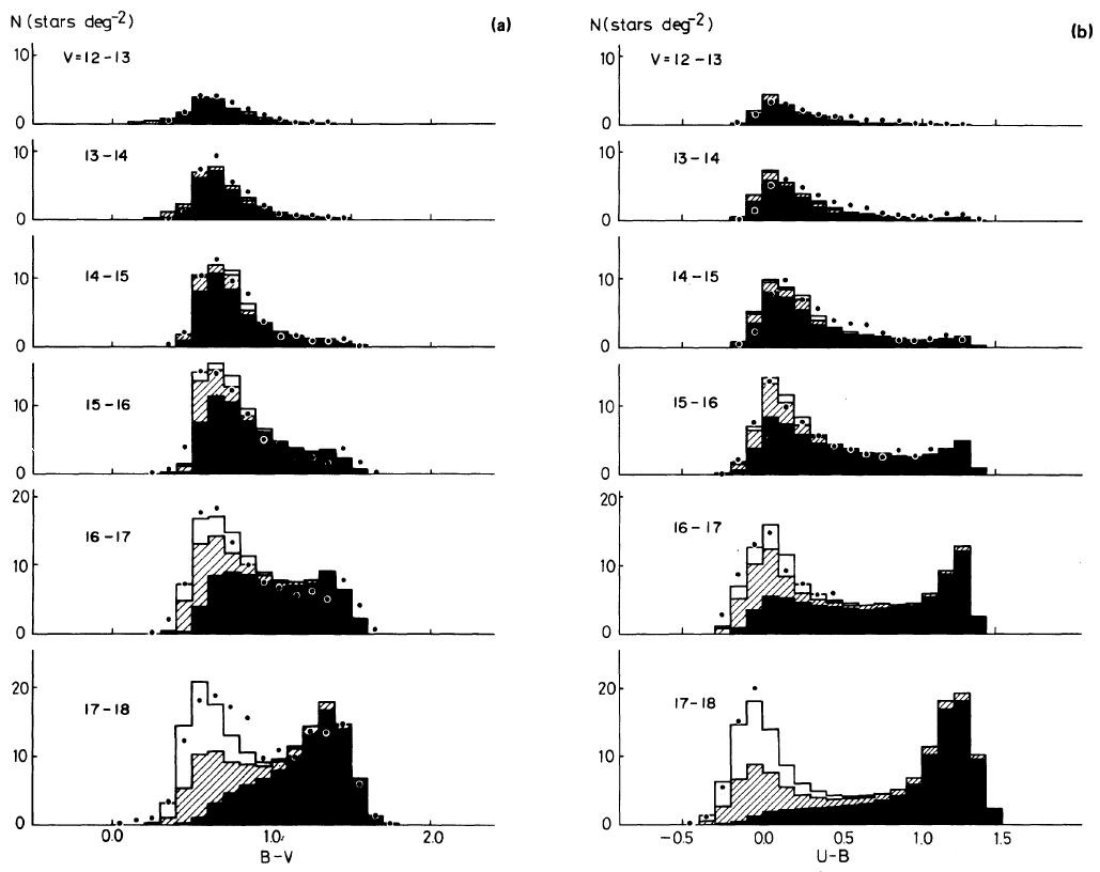
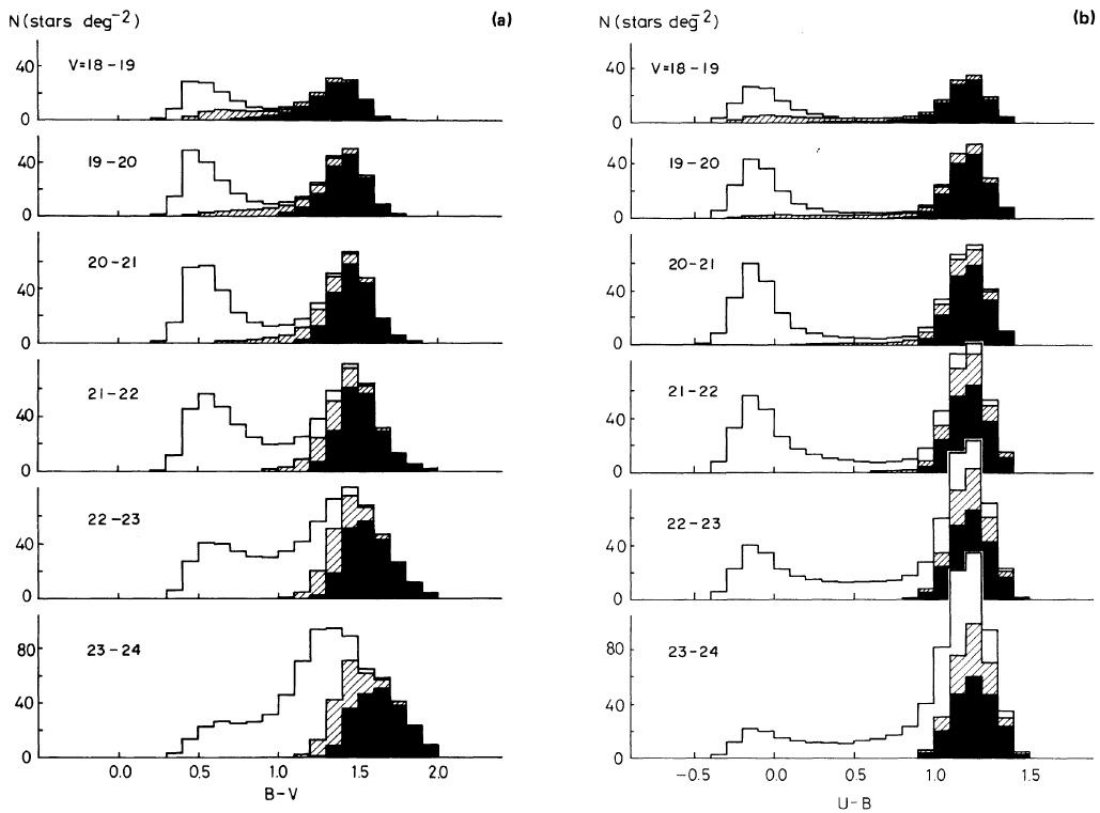
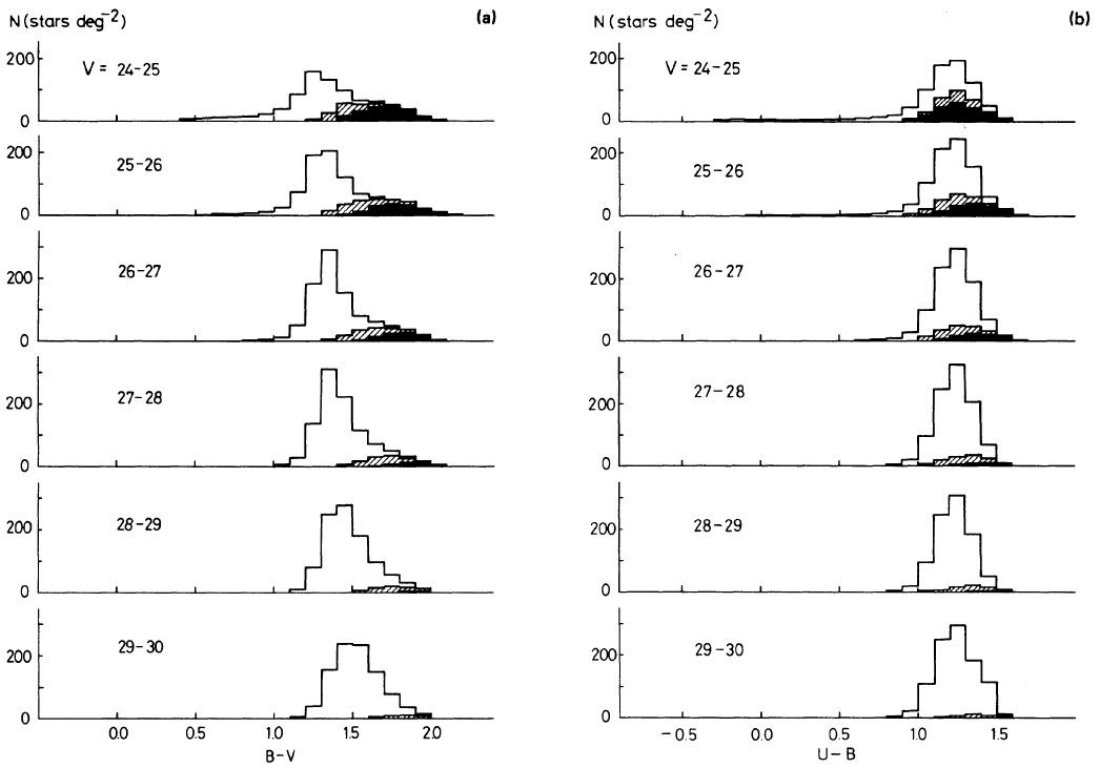
　B-V 分布は Mv - (B-V) 関係から計算された。 U-B 分布は そこに、主系列星（j = 1）と巨星　(j = 2) の二色図を適用して決めた。二色図の 関係はメタル量に依存する。そしてメタル量は高度 z の関数と考えられる。

　　　　　　　CB-V = Gj(Mv, [Fe/H])　　　　　　　　 　　　　　(3)

　　　　　　　CU-B = Hj(CB-V, [Fe/H]) 　　　　　　　　　　　(4)

　　　　　　　[Fe/H] = g(z)　　　　　　　　　　　　　　　　　　　(5)

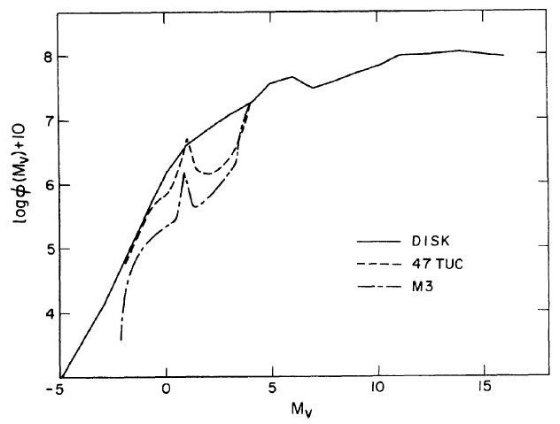
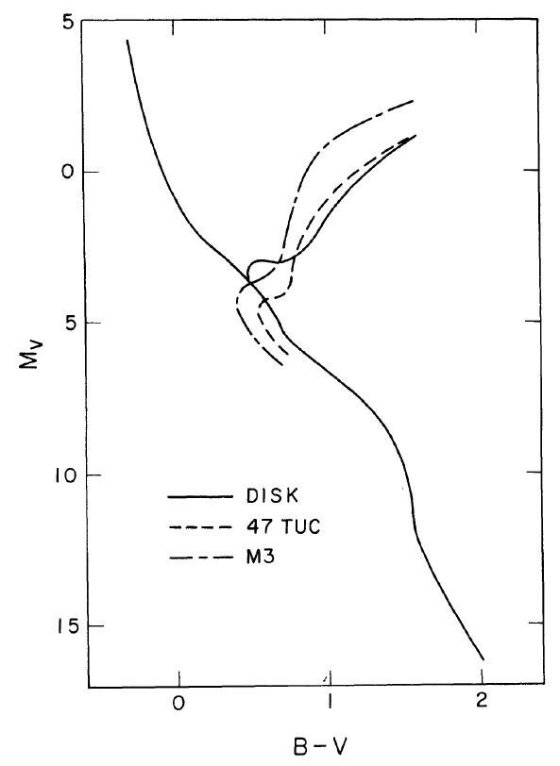
図１．太陽近傍([Fe/H]=0.0)、47 Tuc([Fe/H]=-0.64), M 3([Fe/H]=-1.69) の光度関数。 球状星団光度関数が Mv = +4 で近傍光度関数と滑らかにつながることに注意。
　光度関数のメタル量変化 φz(Mv) は図の３本を内挿して作った。




超巨星と準巨星は j = 2 系列に含ませる。白色矮星は考えない。水平枝星のカラー 分布も無視する。すると、星計数は

　　　　　　　A(V, C) = ω Σi,j∫zj (V,C) φj.z(Mv) Di(z) z2dz　　　　(6)

ここに、zj(V,C) は方程式 (2) の解である。

　３．a．銀河面 z = 0 pc での入力データ　

　光度関数　

　円盤光度関数 φz=0pc(Mv) の主要部 Mv = -4 ∼ +14 は McCuskey 1966 の図６を採用した。図１を見よ。この関数は 0.093 星 pc-3 で、Wielen et al 1983 の 0.11 星 pc-3 より少ない。少ない方を選んだ 理由はシュミット乾板では連星や多重星が分解されないからである。光度関数は Mv = +7 付近に浅い窪みを有する。これは、 Wielen 1974 にも現れて、"Wielen dip" と呼ばれている。Mv = +14 付近の反転は本当のようである。 我々は Mv = +20 までゆっくりした低下を仮定した。明るい方では Mv = -4 を最高 光度とした。

　主系列星と巨星の割合　

　z = 0 pc における、等級毎の主系列星の割合 F(Mv) は Miller, Scalo 1979 から 採った。その F(Mv) を用いて、

　　　　　　　φj=1, z=0pc(Mv) = F(Mv)φz=0pc(Mv)　　 　　　　　(7a)

　　　　　　　φj=2, z=0pc(Mv) = [1 - F(Mv)]φz=0pc(Mv) 　　　　　(7b)

図２のHR図上では、[Fe/H]=0 に対し、j = 1 主系列と j = 2 巨星系列が実線で 示されている。主系列星は -4 ≤ Mv ≤ +20 に渡って存在する。一方、 巨星枝は Mv ≤ +3.7 のターンオフより明るい側にのみ存在する。

　図３では同様のラインを２色図上に引いた。

図２．実線＝M 67 巨星枝＋ Wielen 1974 太陽近傍主系列。
　　　点線＝ M3, 47 Tuc の HR 図


　　　　　図３．[Fe/H] = 0(観測値), -1(モデル), -2(モデル) に対する２色図。 (左)： 主系列星　(右)： 巨星。

　３．ｂ．低メタル星の入力データ　

　[Fe/H] ≥ -0.64 星の光度関数　

　ある場所での平均メタル量は平均年齢と銀河平面からの高さの二つの関数と 考えられる。しかし、低メタル星の光度関数は良く分からない。そこで、 平均メタル量が 47 Tuc の値 [Fe/H] = -0.64 まで下がるまでは、 前節で求めた銀河面の光度関数を代用する。

　-1.69 ≤ [Fe/H] ≤ -0.64 星の光度関数　

Schmidt 1975 によると、高速度星を用いたより低メタルの星の光度関数は、+5 ≤ Mv ≤ +12 では 円盤と同じ形である。そこで、+4 ≤ Mv ≤ +20 では銀河面の光度関数と同じ と仮定した。 Gilmore, Reid 1983 は z = 5 kpc までは、Mv < +4 の明るい星の数が高度と共に減少して行くこと を示した。この傾向は図１に示された球状星団において見られるものとよく似ている。 [Fe/H] ≤ -0.64 (47 Tuc) では主系列星光度関数は σm = 0.7 で コンボルブして、 F(Mv) を調整し、主系列星の数がターンオフで巨星枝につながる ようにした。

　　　　　　　F(Mv) = exp[-(Mv - Ma)2/2σm 2],　　(Mv < Ma)　　　(8a)

　　　　　　　F(Mv) = 1 　　　　　　　　　　　　　　　　　(Mv ≥ Ma)　　　 (8b)　　

ここに、 Ma = Mv(TO) + (2ln2)1/2σm である。 図１の説明にもあるように、 -1.69 ≤ [Fe/H] ≤ -0.64 間での任意のメタル量に対する光度関数は、 47 Tuc と M 3 の光度関数の間の内挿で決まる。

はっきりしないのは、ここで決めた光度関数は式(6) の何に当たるのか？特に円盤光度関数と楕円体光度関数を足したものなのか どうか？ 		　(B-V) - Mv 関係　

　M 67, M3, 47 Tuc の (B-V) - Mv 関係を内挿することで、任意のメタル量に対する 色等級関係を導いた。 （内挿する際、B-V 一定でやるのか、質量一定でやるのか、 光度一定か？） 我々は TO より明るい主系列星、巨星を棄てないので、（式(8) 参照）色等級関係は TO より先、青い領域まで、ΔMv/Δ(B-V) 一定で外挿される。赤い方にも (B-V) ∼ 2.0 まで Wielen 1974 の関係と等級差一定のままでなぞることで外挿した。

　二色図のメタル量による変化　

　主系列星と巨星の (U-B) - (B-V) 関係がメタル量でどう変化するかが図３に示さ れている。[Fe/H] = 0.0 は観測値、-1.0, -2.0 はモデルである。よく知られて いるように、低メタル F - G 型矮星はブランケッティング効果により強い (U-B) 超過を示す。(Wildley et al 1962) δ(U-B)0.6 , Sandage 1969, は B-V = 0.6 での値に修正した(U-B) 超過値である。ブランケッティングラインの勾配 Δ(U-B)/Δ(B-V) を使って （？）　 δ(U-B)0.6 一定の線を二色図上に描いた。図３に [Fe/H] = 0.0, -1.0, -2.0 のラインが引いてある。このラインは Garney 1979 による δ(U-B)0.6 と [Fe/H] の関係を用いて作ったものである。この 等メタル線は B-V ≤ 0.2 では一本に融合する。高温星ではメタルがオパシティに 効かないからである。B-V ≥ 1.4 では不確定さが大きいのでこの部分は無視する。
　低メタル巨星のモデル二色図は Arimoto.Yoshii 1986 により作られた。本研究で 特に重要な準巨星の二色図は観測に基づいて得られた。準矮星は矮星の二色図を U-B でプラス方向に 0.02 等ずらして作った。



　４．銀河系モデルの構築　

　４．a. 円盤成分 Di=1(z)　

　円盤密度分布は下の形をとる。図４に示すように、スケール高 hi=1(Mv) は Mv によって変化する。巨星のスケール高は 250 pc としたがこれはあまり結果に 影響しない。

　　　　　　　Di=1(z) = exp[ - z/hi=1(Mv)]　　　　　　　(10)

　４．a. 中間成分 Di=2(z)　

　中間成分はあるのか？　

　中間成分は幾つかの S0 銀河、円盤銀河 NGC 4565, バルジの大きな幾つかの 円盤銀河で見つかっている。また、Blaauw 1965 によるといくつかの変光星は中間種族 に属する。それにも拘らず、銀河系の中間種族の存在は決着がついていない。反対論 については、 Bahcall、Soneira 1984 を見よ。

　中間成分の密度関数は円盤と同じ指数関数型を仮定する。

　　　　　　　Di=2(z) = fi=2 exp[ - z/hi=2] 　　　　　(11)

fi=2 に関しては、 Bahcall、Soneira 1980b が 5 % 以下とし、Pritchet 1983 は 5 % としている。 Yoshii 1982, Gilmore,Reid 1983 は hi=2 = 1 - 2 kpc とした。

図４．Mv による円盤スケール高変化。矮星データは Miller,Scalo 1979 より。


　４．c. 楕円体成分　 Di=3(z)　

　Di=3(z) はドボークルーの r1/4 則に従う。

　　　Di=3(z) = fi=3 exp[ - b re-1/4(s1/4 - ro1/4)] (s/ro)-7/8 (12)

　　　s2 = ro2 + z2/q2 　　　　　　　(13)

ここに q は軸比、b = 7.669 は定数、ro = 8 kpc は太陽の銀河系中心距離、 re は遠方から観測した時の半分光度半径で銀河系では ro/3 程度である。 Bahcall、Soneira 1980b は (12) 式の密度分布で V = 20 - 22 mag の (B-V) 分布を上手く説明できることを 示した。我々は彼らの結果を参考に、 q = 0.9 とする。

最後に残るパラメターは fi=3 である。べき乗型密度則は銀極方向では （１２）式とよく似ているのでここでは扱わない。

　４．d. メタル分布 g(z)　

　メタル分布は３つの折れ線で表わす。

　　　　　　　g(z) = max (g1, g2, g3)　 　　　　　　(14)

　　　　　　　g1 = α z

　　　　　　　g2 = β - (β - γ)z/7000

　　　　　　　g3 = γ

g1 は z = 0 pc から 1000 - 2000 pc までの領域を表わす。 α は -0.8 から -0.3 の範囲で星毎に様々な値が様々な研究者により得られ ている。g2 は z = 1000 - 2000 pc 領域の中間領域を示す。 g3 = -1.5 は z = 7000 pc より先を示す。

　４．e. モデルの作り方　

　大事な四つのパラメター　

　決めなければいけない大事なパラメターは、中間成分の規格値 fi=2, と スケール高 hi=2 である。メタル量勾配 α は主に円盤成分と 関係し、漸近値 β は中間成分と関係する。

　その他のパラメター　

　その他に、円盤晩期型矮星のスケール高 hi=1(Mv > +5) と 楕円体成分の規格値 fi=3 も補助パラメターとして必要である。 我々はまずこの補助パラメターに尤もらしい値を入れ、次に α を順次 変えながら残りの主要パラメター三つを決めて行くという手法を採用する。

　４．f. 星計数データ　

　銀河モデルでシミュレートする等級帯は V = 12 - 18 である。ここは数も十分あり、 銀河の混入が少ないからである。この等級区間を ΔV = 1 に分割し、それを カラー (B-V) = -0.4 ∼ +2.0 で Δ(B-V) = 0.1 の 24 ビンに分ける。 10,065 観測星 を 6 × 24 = 144 ビンに振り分けると、 33 ビンは空であった。 一方、 36 ビンには 100 個以上の星が含まれる。B - V ≥ 1.5, V = 17 - 18 の ビンの星数は精度が低い。同じ V ステップは U-B に関して同様に -0.8 ≤ U-B ≤ 1.6 を 0.1 刻みにビンが区切られた。ただし、U ≥ 18 ではデータが不完全 なので V = 15 - 16, U - B ≥ 1.1 の 5 ビン、 V = 16 - 17, U - B ≥ 0.5 の 11 ビン、 V = 17 - 18, U - B ≥ -0.1 の 17 ビンは除外した。その結果、112 ビンに 6238 星を配布することになった。内、23 ビン は空、 21 ビンは 100 以上の星を含む。モデルフィットは、

　　　　　ρ2 = ΣB-V(Nobs - Nmod) 2 + ΣU-B(Nobs - Nmod) 2　　　(16)

を極小化することで決める。

　　　　　表１．銀極方向 21.46 deg2 の観測星計数データ


　５．結果　

　５．a. 二成分銀河系モデル　


図５．二成分モデルでの最小二乗和 ρ2。横軸はメタル量勾配 α。 モデル(1)＝ 円盤＋中間(矮星＋巨星)、モデル(2)＝ 円盤＋中間(矮星)、 モデル(3)＝円盤＋ハロー

　モデル(1)＝ 円盤＋中間(矮星＋巨星)　

　fi=2 = 0.0142, hi=2 = 1512 pc, α = -0.50 kpc -1, β = -0.615 で極小値 ρ2 = 255 を得た。 Yoshii 1982, と似ている。

　モデル(2)＝ 円盤＋中間(矮星)　

　このモデルは 主系列星のみを含む。 fi=2 = 0.0204, hi=2 = 1335 pc, α = -0.40 kpc -1, β = -0.363 で極小値 ρ2 = 319 を得た。 Gilmore,Reid 1983 と似る。

　モデル(3)＝円盤＋ハロー　

fi=3 = 0.00197, α = -0.70 kpc -1, β = -0.711 で極小値 ρ2 = 365 を得た。 Bahcall、Soneira 1980b と似る。

図６.(上)二成分モデルの密度分布。z = 0 pc で太陽近傍 Mv ≥ 4 密度。
　　 (下)二成分モデルのメタル量分布。実線＝モデル(1), 破線＝モデル(2), 一点鎖線＝モデル(3)


　モデル間の比較 - 1　

　図５で明らかなように、モデル(1) が最もフィットがよい。中間成分に巨星を 含ませた効果は、

(i) 　巨星系列を考慮しないと、進化した星を主系列星と看做すため fi=2 が大きく見積もり過ぎ、 hi=2 を小さく見積もり過ぎる。なぜなら、 モデル (i),(ii) がシミュレーションする中間成分の対象は同じ観測データだからである。

(ii) 　(B-V) カラー分布はターンオフ B-V ∼ 0.5 mag 付近にピークを持つ。 ピークの青い側は主系列星、赤い側は大体同じ等級の準巨星からの寄与が効いている。

したがって、準巨星の寄与を無視すると、ピークの赤い側にいた星が青い側に移り、 ピーク位置が青い方に移る。この青方移動を埋め合わせるには、ターンオフカラーを メタル勾配を緩くして赤くする必要があり、α を小さくして最小二乗を極小化 するのである。

　モデル間の比較からの結論　

　ρ2 極小に関してはモデル (1) が良好である。これは巨星を考慮 することが重要であることを示す。V = 12 - 18 データのフィットから次の３点が浮かび 上がってきた。

（A).　中間成分は定量的に評価できる。
（B).　メタル量勾配は 0.5 ≤ z ≤ 5 kpc の星から決められる。
（C).　準巨星の役割が大きい。

さらに楕円体成分は V ≥ 20 mag. で主要な寄与をすることが知られている。だから、 銀河全体では三成分モデルが必要になる。


　５．b. 三成分銀河系モデル　

　最良フィット解　

　スタートモデルは前節のモデル (1) である。そこから、 fi=3 を 0 から 0.0025 まで順次増加させていく。こうして得た最良解は

　　(fi=2, fi=3, hi=2, α, β) = (0.0224, 0.001, 952 pc, -0.50 kpc-1, -0.762)

であった。



図７．三成分モデルにおける最小二乗和のメタル量勾配による変化
　　　晩期型星円盤スケール高 = 325 pc(実線), 345 pc(破線)を固定して、異な
　　　る fi=3 に対し fi=2, hi=2, α, β を変化させてフィットするモデルを探した。
　　　適用 fi=3 はカーブの横に書いてある。最も良いフィットは
　　　 fi=3 = 0.001, hi=1(Mv > +5) = 325 pc で得られた。 		そのときの ρ2 = 231 である。 fi=3 = 0.001 は Schmidt 1975 の得た fi=3 = 0.00125 に近い。

　円盤スケール高の影響　

　適用した円盤スケール高が小さいために存在しない中間成分を産み出したの かも知れない。ところが、円盤スケール高を 325 pc から 345 pc に増加させると ρ2 極小値は 231 から 268 へと増加する。それにも拘らず、 中間成分の解はあまり変化しなかった。これは円盤スケール高を間違えた値に したため中間成分が産み出された説を否定する。

　メタル量勾配　

　図７を見ると、メタル量勾配 α = -0.5±0.1 程度であることが 判る。メタル量勾配が変わると中間成分にどう影響するかを見るため、 α = -0.6 に対してフィットした結果は、 fi=2 = 0.0173, hi=2 = 1040 pc で、最良解とあまり 変わらない。したがって、中間成分のパラメターとして、 fi=2 = 0.02, hi=2 = 1 kpc 程度は安全に言える。




図８．三成分モデルの密度、メタル量分布。


　６．最良フィットモデルの特徴　

　(B-V), (U-B) カラー分布の最良フィットを最小二乗法で定めた結果が表２に 示された。表では以前の結果との比較もされている。

　６．a. 星計数　

　モード距離　

　図９には星計数を示した。細線は各成分からの寄与で、太線が総計である。V = 10 - 18 で観測との一致は良い。Jarvis, Tyson 1981 の V = 14 - 24 の結果ともよく 合っている。 注意するのは、星計数に最大の寄与があるのは D(z)z2 が モード値を採る付近である。指数関数型の密度分布ではメジアン距離が 2.67 h, モード 距離が 2.0 h である。

　Wielen の窪み

図９を見ると分かるように Wielen の窪み Mv ∼ +7 は 星計数の勾配を V = 17（円盤）, 19（中間）, 22（楕円体） で緩めている。これらの 値は距離指標 distance modulus = 9(=17-9), 12(=19-7), 15(=22-7) に相当する。 ただし、総星計数に影響するのは円盤の Wielen の窪み のみである。したがって、 実際に中間成分と楕円体成分が Wielen の窪み を有するかどうかは確かでない。

V = 16 - 20 で観測星計数の勾配が緩むのは Bahcall, Schmidt, Soneira 1983 では、光度関数の勾配が現れるからである。まさにそれなのか？


表２．最良フィットモデルのパラメター

　６．b. カラー分布　

　中間成分が円盤と楕円体の間に独自に現れることは ない。

　図１０，１１、１２は B-V, U-B カラー分布を示す。図１０には 12 &le, V ≤ 18 での観測分布も黒点で示した。一致は良い。分布の最も大きな特徴は双峰性である。 等級変化に対してカラー変化が小さい所でカラー分布はピークを示す。 B-V に関して は B-V ∼ 0.5 （Mv ≈ ４−６）と 1.5 (Mv ≈ 9 - 13)付近である。 前節に述べた通り、円盤、中間、楕円体でモード距離指標は数等づつずれている。 中間成分の 16 < V < 18, 楕円成分の 19 < V < 21 は B-V ∼ 0.5 付近に集中する。一方、円盤星の 18 < V < 22 は　B-V ∼ 1.5 付近に 集まる。したがって、三成分が同時に寄与するのは V = 19 - 21 の間のみである。 そこではカラー分布は双峰性で中間成分が円盤と楕円体の間に独自に現れることは ない。

　楕円体成分を円盤成分から分離する　

　U-B の場合には二つの峰は U-B = -0.1 と 1.2 ではっきりと現れる。これらの カラー分布は楕円体成分を円盤成分から分離するのに有用である。V = 19 - 21 では 楕円体星の 90 % は　B-V ≤ 1.0 か U-B ≤ 0.5 であり、V = 21 - 22 では 　B-V ≤ 1.2 か U-B ≤ 0.9 である。そして、 V > 24 では楕円体星が 支配的となる。


図９．星計数。太い実線＝最良解。薄い実線＝円盤、中間、楕円体寄与。
　　　黒丸＝本論文の観測。白丸＝Jarvis,Tyson 1981



図１０．各等級区間での (a) (B-V), (b) (U-B) 分布モデル。黒点は観測値 (表１参照)。　黒＝円盤、斜線＝中間、白＝楕円体



図１１．より暗い（観測データなし）等級でのカラー分布



図１２．さらに暗い（観測データなし）等級でのカラー分布





 　巨星の役割　

　巨星の役割はカラー分布ではっきりしている。V ≤ 12 の円盤星、V ≤ 18 の中間成分、楕円成分では Bahcall, Soneira 1984 が示したように巨星の割合が高い。図１３にその様子を示した。図 13(a) にあるように 円盤成分では巨星枝星が、。図 13(b), (c) にあるように中間成分と楕円成分では 準巨星が最も重要である。特に準巨星は (B-V)分布のピークを赤い方にずらす働き をする。楕円体 B-V 分布ピークはメタル量勾配があっても中間成分と似た位置にくる。

　赤色巨星　

　球状星団の光度関数（図１）に現れる Mv ∼ +1 のコブには水平枝星が含まれる。 しかし、われわれは Mv ∼ +1 の星全てを赤色巨星とした。しかし、中間成分と 楕円体成分中の赤色巨星の割合は小さいのでこの扱い方による影響は無視できる。 観測された青い星 B-V ≤ 0.2 の星の数が少ないこともこの措置を支持する。




図１３．モデルのカラー分布。斜線＝主系列星。白枠＝巨星。
　　　　(a) V = 10 - 11 円盤星の (B-V) 分布。
　　　　(b) V = 17 - 18 中間（上）と楕円体(c) の (B-V) 分布。
　　　　(c) （b）と同じ。ただし、 (U-B) 分布。


　６．(c). 光度、質量、星数の表面密度　

　表面光度　

　光度、質量、星数の表面密度を図１４に示した。最良フィット銀河モデル の表面光度は 25.3 Lo pc-2 で、内 89.5 % は円盤、8.9 % は 中間成分、1.5 % が楕円体である。円盤の内でも -1.0 ≤ Mv ≤ 2.0, 0.5 ≤ B-V ≤ 1.0 の巨星が光度の大部分に寄与している。

　星数柱密度　

　星数は 66.0 星 pc-2 である。円盤、中間、楕円体がそれぞれ 92 %, 6 %, 2 % 寄与している。図１４を見ると、 Wielen のこぶが σN, σM にはっきりと現れている。

　６．(d). メタル量　

　三成分の それぞれに一定メタル量を付加するモデル　

　最良フィットでは d[Fe/H]i=1 = -0.5 kpc-1, d[Fe/H]i=2 = -0.1 kpc-1 である。しかし、三成分の それぞれに一定メタル量を付加するモデルも可能である。そのようなモデル で試してみた結果、ρ2 は非常に悪かった。 　従って、中間成分の星は一定のメタル量を持つというよりは、銀河面から の距離に応じてメタル量が変化すると考えるべきである。

　中間成分の起源　

(i) 原始円盤のなかで中間成分星が発生した。原始円盤は星形成を継続し、 メタル量を上げながら収縮して現在の円盤になった。そのため低高度ほど 高メタルになった。円盤と中間成分は一つ過程の別の段階での生成天体である。

(ii)　銀河系は二段階で形成された。その一つの説は分子雲による重力散乱で 弾かれた星が集積して中間成分を作った。別の説はバルジが円盤の重力場に 反応して変形し厚い円盤となった。

　現在の段階ではどれが正解か判断できない。しかし、中間成分のメタル量が 一定というモデルの ρ2 が大きいことは重大な手掛かりである。

図１４．表面光度密度 σL(Lo pc-2), 表面質量密度 σM(Mo pc-2),
　　　　表面数密度 σN(stars pc-2)。
　　　　破線は Wielen のコブを入れないモデル。
　 　　　　σLは表面輝度とは異なる。 これいいのか？


　７．結論　

　 色―見かけ等級図を (B,V), (U,B) の組で合わせたことになる。三次元で合わせたら もっと分かりやすいか？赤外を入れたら？


　 中間成分が支配的（頭を出す）等級、カラー区間はないのはこの成分を文句なく 認めるには弱い原因だ。