Density Distribution of Faint Stars in the Direction of the North Galactic Pole

　２．観測データ　

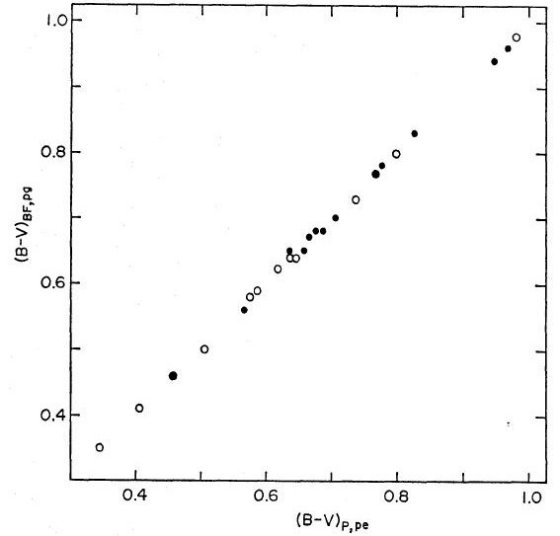
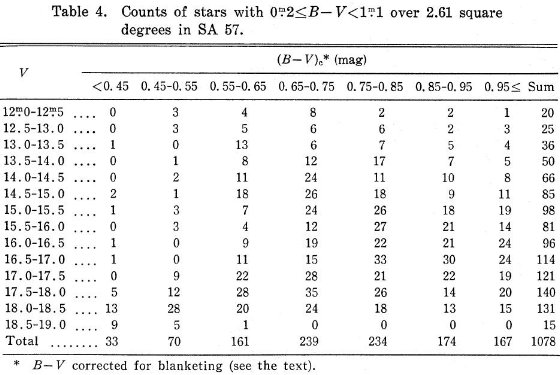
図１．写真カラー (B-V)BE, pg Becker, Fenkart 1976 と光電カラー (B-V)P, pe Purgathofer 1969 との比較。黒丸＝δ(U-B) < 0.1, 白丸＝δ(U-B) > 0.1 の星。 　SA 57 データ　 　SA 57 データは Becker, Fenkart 1976 の３色測光カタログを使用した。カタログ には 2.61 deg2 内 1816 星の RGU 等級が G = 19.5 mag まで載っている。 これらの星は次の６種類に分類された。Ｄ＝円盤星、Ｈ＝ハロー星、Ｗ＝白色星、 Ｒ＝赤色星、Ｎ＝拡がった像、ｂｌ＝重なった星。我々はＤとＨのみを用いる。これ らは良く定義されたＦ，Ｇ，Ｋ型星である。W はおそらく、白色矮星か QSO であり、 R は G-R=1.6 (B-V=1.2) より赤い星である。 　バンド変換　 　SA 57 標準星の UBV 光電測光の結果 は Steinlin のアイリス・等級曲線を 用いて RGU システムに変換されている。これらの星は紫外超過の少ない 種族 I 主系列星である。そこで、問題は上の変換を用いて逆変換により RGU システムから UBV システムに移った時、紫外超過の大きい星の誤差がどのくらい になるかということである。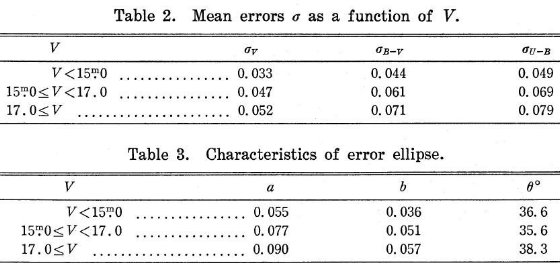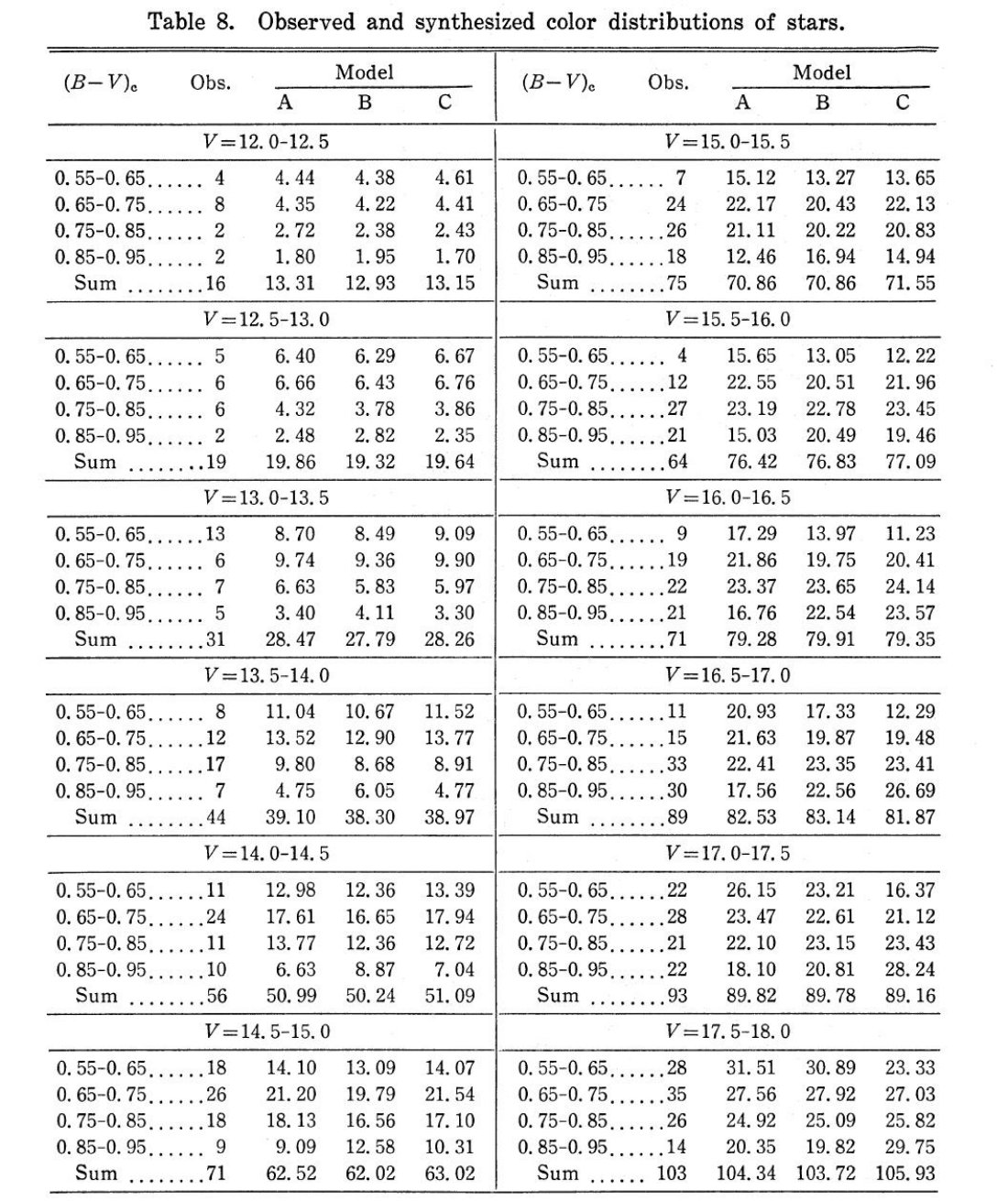 　表１には標準星 B-V ≤ 1.0, V ≥ 12 の データを載せた。 　第３列＝写真等級 VBE, pg 。第４列＝ 写真カラー (B-V) BE pg。第５列＝写真カラー (U-B)BE, pg。 第６列＝ Purgathofer 1969 カタログ番号。第７列＝光電等級 VP, pe 第８列＝光電カラー (B-V)P, pe。第９列＝ 光電カラー (U-B) P, pe。第１０＝ は紫外超過 δ(U-B) である。 　紫外超過の大きな星の変換式　 　図１では写真カラー (B-V)BE, pg Becker, Fenkart 1976 と光電カラー (B-V)P, pe Purgathofer 1969 とを比較した。黒丸＝δ(U-B) < 0.1, 白丸＝δ(U-B) > 0.1 の星。黒丸も白丸も 0.01 等の範囲で 一致しており、紫外超過が大きくても URG から UBV への同じ変換式が使えることが わかった。

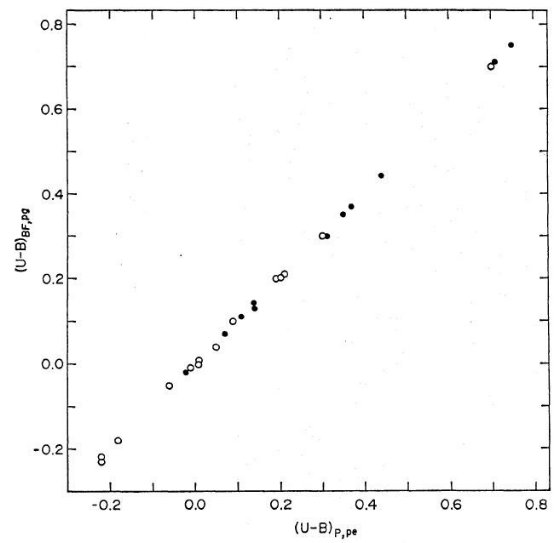
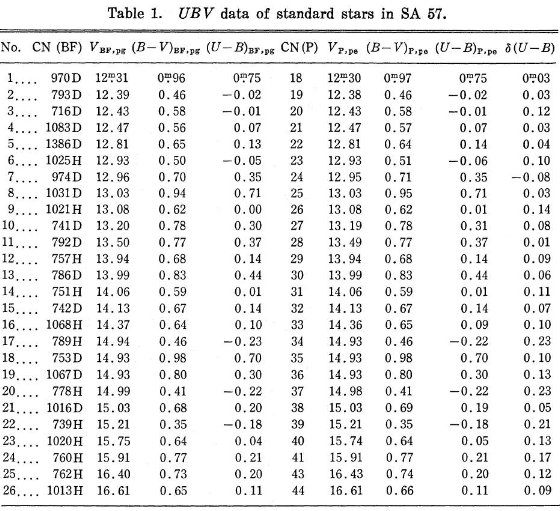
図２．写真カラー (U-B)BE, pg Becker, Fenkart 1976 と光電カラー (U-B)P, pe Purgathofer 1969 との比較。黒丸＝δ(U-B) < 0.1, 白丸＝δ(U-B) > 0.1 の星。 表１．SA 57 標準星の UBV データ

表２．等級 V による平均誤差 σ の変化 表３．誤差楕円の特性 　誤差分布　 　UBV のエラーは観測エラーと変換エラーから生じる。観測エラーと比べると変換 エラーは無視できるほど小さい。表２に V, (B-V), (U-B) の平均誤差を載せた。 以下では、観測エラーにより観測等級はその平均等級の周りに正規分布すると考える。 ２次元正規分布は以下のように表わされる。 f(x,y) = 1 exp [ - 1 E(x,y) ] 2πσxσy (1 - ρ2)1/2 2 E(x, y) = 1 [ (x-⟨x⟩)2 -2ρ (x-⟨x⟩)(y-⟨y⟩) + (y-⟨y⟩)2 ] 1 - ρ2 σx2 σxσy σy2 ここに ρ は相関係数である。表２の σB-V, σU-B を適用して、図３に E(B-V, U-B) = 1 で定義される誤差楕円 を描いた。星がこの中に入る確率は 39 % である。表３には誤差楕円の主軸と副軸の 長さ、及び主軸が B-V 軸と成す角 θ を載せた。 　ρ をどう決めるのか？　U, B, V エラーが与えられた時に、 U-B と B-V のエラーには相関が生じるからか？すると σU, σB, σV から ρ を得る式が存在するはずだが。

図３．太い実線＝ヒアデス主系列。細い実線＝ブランケッティング線。それぞれは (B-V)e = 0.45, 0.55, 0.65, 0.75, 0.85, 0.95 を持ち、V < 15.0, 15.0 < V < 17.0, 17.0 <: V の３本の支線に分かれる。これは、等級により 観測誤差の影響（表２，３）が異なるためである。図中に挿入した略図は細線がどう 計算されたかを示す。

　３．星計数（Star Count）　

２色図をブランケッティングラインで区分する　 　２色図上、低メタル星はヒアデスラインの上にくる。主系列星はブランケッティング ラインに沿って絶対等級が変化しない Widley et al 1962 ことが知られている。そこで、２色図上の星をブランケッティングラインで区分する。 そしてその区分内の星は同じ絶対等級を持つと考えて星計数を行うという手法を採用 する。 　観測誤差とメタル効果を考慮した絶対等級 一定ライン　 　星がヒアデスラインから、観測エラーでずれる確率を p, メタル量の違いで ずれる確率を 1-p とする。図３の略図で星が観測エラーのため点 Q にいたとする。 その場合、絶対等級はＱ点を中心とする誤差楕円がヒアデスラインに接する点 (B-V)1 に対応する量となる。その接触楕円を E(B-V, U-B) = ct と表わす。(B-V)1 点にいる星が観測誤差で Q 点に ある確率は 　　　　　p = ∫Outside E(x,y)=ctf(x,y)dxdy = exp( -ct)　　　(4)　 である。一方、もし Q 点がブランケッティング効果のための ズレであるなら、その絶対等級はブランケッティングラインがヒアデスラインと 交差する点 (B-V)2 に対応するだろう。 　絶対等級区分けの結果　　 こうして、観測誤差とブランケッティング効果の両方を考慮した絶対等級一定の ラインは 　　　　　(B-V)c = p(B-V)1 + (1-p)(B-V)2 　で表わされる。（疑問多い）

図３には (B-V)c = 0.45, 0.55, 0.65, 0.75, 0.85, 0.95 ラインを 示した。各ラインは V < 15.0, 15 < V < 17, 17 < V の３本の線を 引いた。このラインで分けられた各区分のサンプル星の数を表４に示した。 　星計数のターンオフ不連続　 　V ≥ 13.0 の星計数は (B-V)c = 0.55 で不連続となる。これは ハロー星の年齢効果であろう。これより青いハロー星は既に主系列進化を 終えており、観測される青い星は円盤主系列星か水平枝星であろう。V ≥ 18 に なると観測誤差が大きくなり不連続が目立たなくなる。これは V =18 より暗い 星は統計に使えないことを意味する。 表４．SA 57, 2.61 deg2 での 0.2 ≤ B-V ≤ 1.1 星の星計数

　Mv = 一定線への疑問点　

　４．密度関数の決定　

４．１．統計方程式　 　星計数を行った　 　0.55 ≤ (B-V)c ≤ 0.95 の星を V = 12.0 - 18.0 の間で 半等級区分で星計数を行った。このカラー巾はハロー星の年齢効果が効かず、 円盤星とハロー星が共存している部分である。半等級区間は σV の 数倍ということで決めた。 　星計数の表式　 　星計数 A(mV±l1/4) は光度関数と密度関数の双方に関係する。 したがって、適当な光度関数を採用すれば密度関数を得ることができる。 A ( mV± 1 ) = ωΣi,j ∫ gijφij ( MV± 1 ) Dl(z)z2dz 4 zj 4 ここに、 gij = 1 ∫ 0.95 exp { - [C-Cij(Mv)]2 } dC (2π)1/2σB-V 0.55 2σB-V2 　ここに ω は領域の立体角、φ(Mv±1/4) は pc3 当たり、Mv±1/4 内の星数、C(Mv) は絶対等級 Mv とカラー C の関係、D(z) は密度関数である。添字 i は円盤星かハロー星か、j は主系列星か巨星かを示す。 　密度式　 　光度 z と等級 mV は次の関係で結ばれている。 　　　　　　　mV = Mv + 5 log z - 5 + AV 対象とする星は 200 pc 以上の高度を持ち、従って等しい星間吸収 Av = 0.02 を 受けていると考える。密度関数は次の形を考えた。

表４．ハロー主系列星のカラーと絶対等級の関係 　　　　　　　Ddisk = exp(-αd z)　　　　　　　(7) 　　　　　　　Dhalo = α exp(-αh z)　　　　　(8) 　A(Mv±1/4) に表４の星計数を入れ、３つのパラメター α, αd, αh に対する　12 本の式を得る。 この式を最小二乗法で解くことにより、各種族の割合も決まる。

４．２．光度関数　 　円盤光度関数 φdisk(Mv±1/4) には van Rhijn 型光度関数 を McCuskey 1966 から採った。ハローの光度関数 φhalo (Mv±1/4) は確立していない。Mv = 3 - 4 mag. より明るいハロー星は主系列 から進化している。このためハローの光度関数は一般に急である。そこで、３種類の モデルＡ，Ｂ，Ｃを考えた。それらは M 3(Sandage 1957), M 92(Hartwick 1970), φdisk である。ハローの光度関数 φhalo は Mv ≥ 7 では φdisk と一致させる。 　４．３．(B-V)c : Mv 関係　 　(B-V)c : Mv 関係　 　0.55 ≤ (B-V)c ≤ 0.95 での (B-V)c : Mv 関係が 必要である。円盤星は二色図上ヒアデスラインに近いので、 (B-V) = (B-V)c とする。円盤主系列星の Cdisk,MS(Mv) はGliese 1971 を用いる。円盤準巨星、巨星に対する Cdisk,giant(Mv) は Chiu 1980 の M 67 赤色巨星枝を用いた。準巨星の絶対等級は B-V では殆ど変わらないので 準巨星のカラー分布は Weistrop 1972 の M 67 の B-V 分布を用いた。 　ハロー主系列　　 　ハローモデルＡ，Ｂ　に対してはChalo,MS(Mv) と Chalo,g(Mv) が必要である。M 92, M 3 の UBV データから ブランケッティング効果を補正した (B-V)c が計算された。この (B-V)c に Mv を対応させてプロットし、眼視により、主系列の 暗い端から赤色巨星に至る平均ラインを引いた。V ≥ 18.5 に関しては データが少なく不確定なのでSvhmidt-Kaler 1965 の主系列星を用いた。結果は 表５に与えた。この関係はメタル効果が補正済みなので M 3, M 92 双方に 使用される。 表５．ハロー主系列星のカラー対絶対等級関係

ハロー巨星　 　Bell 1972 によると、巨星には重力効果があるため、二色図上でメタル量効果 による移動方向はブランケッティング効果とは異なる。この理由で、 M 92 と M 3 の赤色巨星の関係は別々に導かれ表６に示された。夫々のメタル量 をハローに仮定して密度分布が求められる。 表６．ハロー準巨星・巨星のカラー対絶対等級関係

４．４．結果　 　密度分布の比較　 　密度分布 (7), (8) のパラメター ad, ah, α は 表７に、そして各等級毎のカラー分布は表８に示した。密度分布は図４に図示した。 表８でモデルの差が出るのは楕円体成分が優勢になる V ≥ 17 である。モデルＣ は観測と合わないことはすぐ分かる。モデルＡ，　Ｂ　は比較的よく観測を再現する。 したがって、ハロー星の光度関数を種族 I で代行させるのは不適当である。 モデルＡ，　Ｂ　は密度勾配 dlogD(z)/dz は円盤星で -1.4, ハローで -0.2 である。 表７．密度分布式のパラメター。

図４．円盤とハローの密度分布。実線＝Ａ、破線＝Ｂ，一点鎖線＝Ｃモデル。

　５．議論　

表９．近傍でのハロー密度とハロー星の W 速度。 　円盤密度勾配 -1.4 　 　上の結果は Sandage, Katem 1977 と似ている。彼らは球状星団 M 15 周辺の Mv = 8 - 12 前景矮星の数を説明するために d logDdisk/dz = -1.4 を導いた。今回の円盤密度勾配 -1.4 は Oort 1960 の K 型巨星、Weistrop 1972 の円盤主系列 Mv = 3 - 9 に対する結果と　z ≤ 1 kps で一致する。 　z = 3 kpc までの密度分布　 　図５には z = 3 kpc までの密度分布を下の式で導いた。 　　　　　D(z) = Ddisk(z) + [⟨φhalo,ms(Mv) ⟩/⟨φdisk,ms(Mv)⟩] Dhalo(z) ここに、 ⟨φdisk,ms(Mv)⟩ と ⟨φhalo,ms(Mv)⟩ は Mv = 4.5 - 7.0 での平均値である。 これはカラーでは (B-V)c = 0.55 - 0.95 に相当する。上式の角括弧 内の比はモデルＡで 0.61, モデルＢで 0.69 である。 　ハロー密度勾配　 　ハローの勾配 -0.2 は フィールド RR Lyr (Plaut 1970) の -0.1 から -0.3　 と近い。これに対し、 Fenkart 1969, Becker 1970 はずっと急な -0.7 を導いた。 その原因は彼らが巨星を無視し、それらの星を誤って近距離に置いたためである。

図５．円盤密度分布の比較。太実線＝Ａ、破線＝Ｂ，細実線＝ Oort, Weistrop