アブストラクト固有運動が大きく、三角視差も得られている星の完全サンプルに基づき、近傍 光度関数を求めた。低メタル RR Lyr 星の空間運動に基づき、その内で楕円体成分 に属する星の割合を決めた。ハロー星の局所密度は 1.7 × 10-4 Mo pc-3 で、質量比としては 6 % である。これは Ostriker, Peebles が提案したマッシブハローの一桁下である。 |
1.イントロOstriker, Peebles 1973 は銀河系のかなりの質量がハローにあるという提案をした。 重いハローは冷たい円盤がバー不安定を起こすのを防ぐだろう。Ostriker 1974 は さらにこの重いハローが銀河の外側に広がっていれば、宇宙を閉じるのに十分な質量 を与えるだろうと述べた。この論文はハロー星の局所密度を求め、Ostriker, Peebles ハローと比べる。光度関数を決める新しい方法を提案し、運動特性からハロー星を 選択する。 |
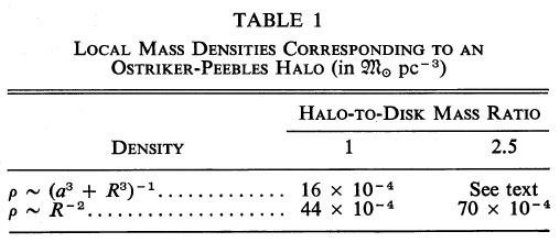
| Ostriker, Peebles 1975 は太陽半径 Ro 内のハロー質量が円盤の 1 - 2.5 倍 あると提案した。Schmidt 1965 の円盤モデルによると、Ro 内の銀河系質量は Ro = 10 kpc として、 0.90 × 1011 Mo である。 ハローと円盤の質量比を 1 - 2.5 とし、ハロー密度則を適当に仮定してハローの 局所密度を求めると右の表1のようになる。 |
 |
|
極大距離 μ = 固有運動、 μ0 = 固有運動サンプル下限値 m = 等級、 m0 = 等級サンプル上限値 p = 年周視差 β = サンプルした天域の割合 とした時、次の極大距離を定義する。 r1 = (1/p)(μ/μ0) = その速度でそこまで遠ざかると固有運動が下限値に達する。 r2 = (1/p) dex [0.2(m0 - m)] = その絶対等級でそこまで遠ざかると見かけ等級が上限値に達する。 rmax = Min(r1, r2) Vmax = (3/4)πβrmax3 ある星 (m, μ,p) に対する極大体積 Vmax はそのような星がこのサン プル内に入る確率が 1/Vmax であることを示す。従って光度関数は Σ (1/Vmax) で構成される。 |
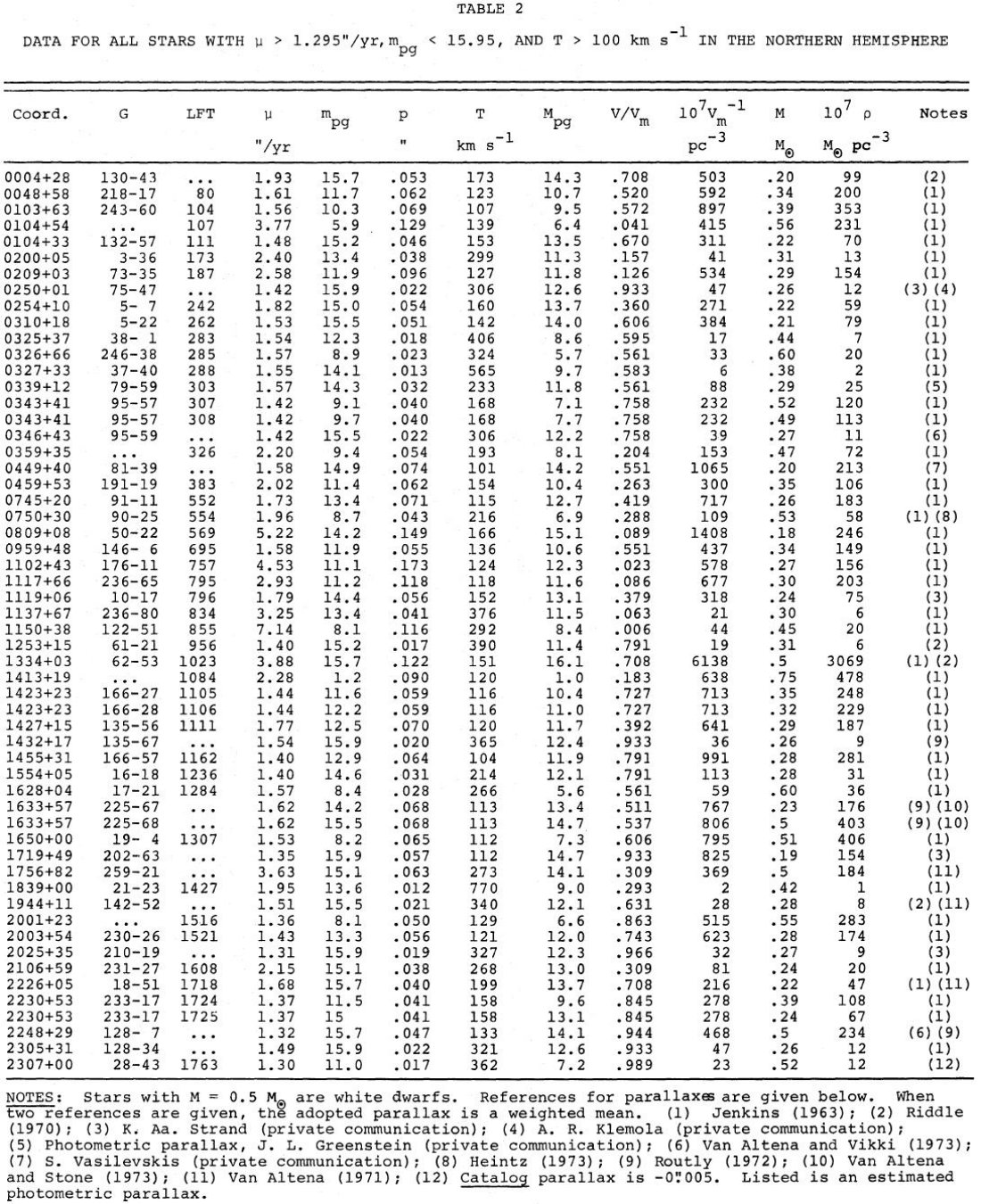
データ 固有運動と年周視差の双方を備えた星の最も広範なカタログは Giclas et al. 1968 である。カタログには写真等級 17 等までの星が収められている。我々は 15.95 等 までの星を使用した。固有運動の完全性を求め、カタログの下限より5倍大きい μ ≥ 1".295 /yr の星を採用した。その結果 126 星が残った。内 111 星は 公表された年周視差データが、残り 12 星は未公表視差があった。 一様性のチェック 各星に対し V/Vmax を計算する。この比は 0 - 1 の区間で一様に 分布するはずである。 126 星の平均は 0.528±0.026 で一様性を支持する。 視差と固有運動から直交速度を計算し、 100 km/s 以上の星 56 星を選んだ。 |
|
高速度星の光度関数 サンプルは直交速度 250 km/s 以上の18星から成る。これらの星の 空間密度は Σ (1/Vmax) = 0.95 × 10-4 pc-3 である。ハロー星の空間密度はこれを2倍して、 1.9 × 10-4 pc-3 である。図1は (1/Vmax)のヒストグラムを示した。図1と同じであるが横軸を 星質量に変えたのが図2である。 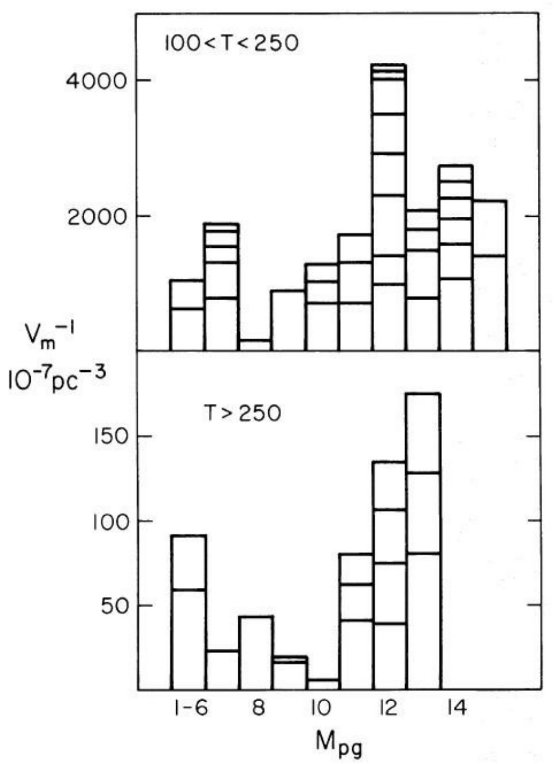 図 1 .1/Vmax のヒストグラム。ハローの光度関数は下図の値を2倍 にして与える。 |
小質量星の寄与 図2は M > 0.25 Mo のハロー星に対しては十分な情報を与えている。それより 小さな星の寄与に対し、サルピータの初期質量関数を仮定して推定するのがよい。 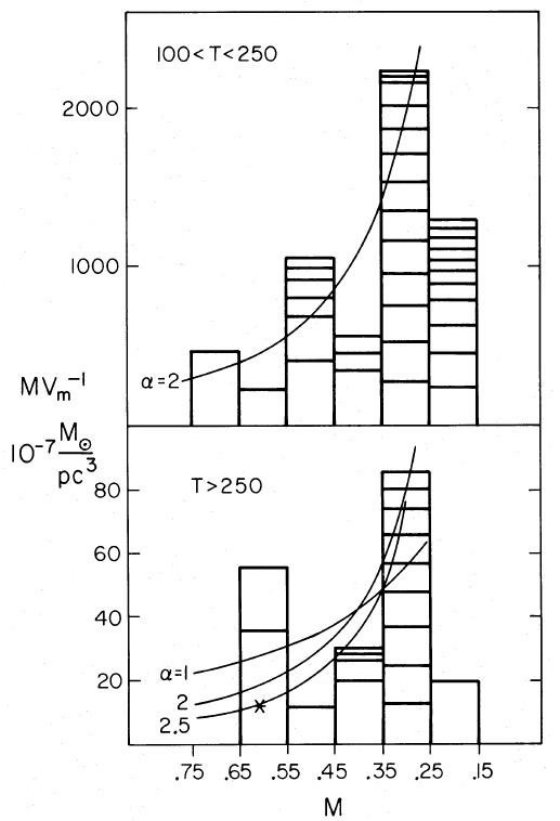 図 2 .1/Vmax のヒストグラム。ハローの質量関数は下図の値を2倍 |