1.イントロ
グリーゼカタログは 1957 年に 20 pc 以内の星のカタログとして発表され、 1969 年の改訂でそれより少し先まで伸ばされた。このカタログは 20 pc 以内 では Mv = +7 より明るい星で完全性が確認されている。それより暗くなると、(a). 南半球は不完全
(b).暗い星は高速度星の場合に検出された。直交速度が小さいと見つけにくい。
(c).検出率低下の影響で、暗い星の見かけ密度は距離と共に急落する。
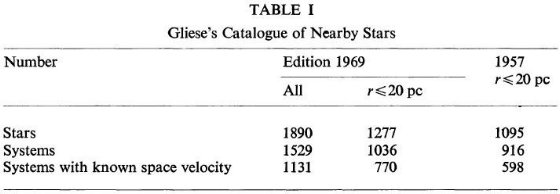
表1.グリーゼカタログの中身
1.イントログリーゼカタログは 1957 年に 20 pc 以内の星のカタログとして発表され、 1969 年の改訂でそれより少し先まで伸ばされた。このカタログは 20 pc 以内 では Mv = +7 より明るい星で完全性が確認されている。それより暗くなると、(a). 南半球は不完全 (b).暗い星は高速度星の場合に検出された。直交速度が小さいと見つけにくい。 (c).検出率低下の影響で、暗い星の見かけ密度は距離と共に急落する。 |
 表1.グリーゼカタログの中身 |
|
グリーゼカタログから以下の星を選んで、光度関数 φ を作った。 Mv < 7.5 r ≤ 20 pc Mv = 7.5 - 9.5, r ≤ 20 pc, δ > -30° Mv = 9.5 - 11.5 r ≤ 10 pc, δ > -30° Mv > 11.5 r ≤ 5 pc, δ > -30° Mv > 13.5 では下限が得られたのみである。φ の単位は (星数/mag/ 20 pc 球) である。光度関数は Mv = 5 - 9 で平坦である。極大が存在するかどうか 不明確だが、Mv,max ≥ 13 らしい。20 pc 内に予想される星の総数 3600 個の うち 3300 (91%) は主系列星、巨星は 27 星(0.7 %), 300 白色矮星が予想されている。 近傍数密度は少なくとも 0.11 星 pc-3 である。 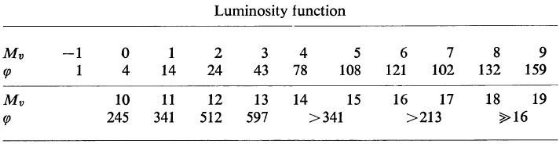 表2.グリーゼカタログから得た光度関数 |
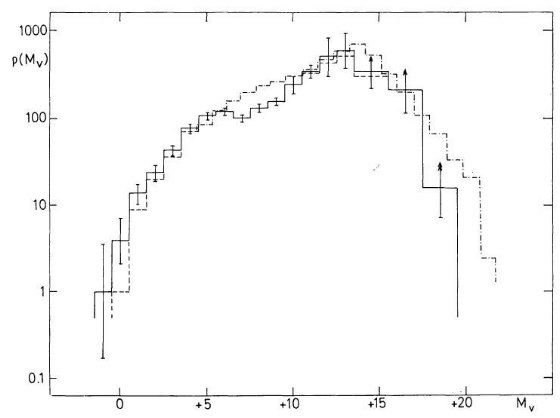 図1.光度関数 φ(Mv) 実線=全 φ, 破線=主系列星の φ, 一点破線=Luyten 1968 |
|
他の光度関数との比較 図1で Luyten の光度関数との一致は驚くべきことだ。方法が全く異なるからで ある。Luyten は固有運動データを使い、星の運動に統計的な仮定を加えて 光度関数を導出したのに対し、今回のは直接星の距離から導いたのである。 Luyten は光度関数のピークが Mv = 13.9(1968), 13.6 (1974) にあると主張した。 図1で Mv = 14 の先の低下はリアルなのかも知れない。明るい方では McCuskey 1966 がより大きな体積から得た値とよく一致している。 質量密度 表3のデータを使い、近傍密度として 0.046 Mo pc-3 を得た。 Mv > 13.5 に Luyten の光度関数を援用しても、 0.049 Mo pc-3 にしか上がらない。この値は力学的に決めた 0.15 Mo pc-3 (Oort 1965) よりずっと小さい。 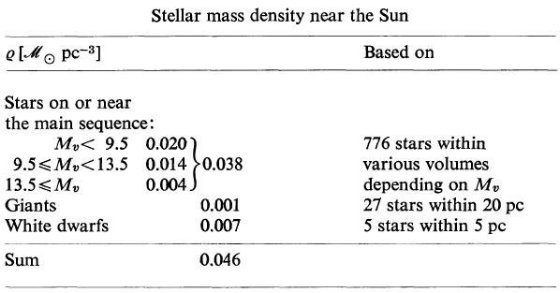 表3.近傍の質量密度 |
運動特性(年齢)との相関 Mv = 5 より明るい星は評価しにくい進化の影響を受けているので対象から外す。 それより暗い星は主系列星と考える。それらの星の光度関数は基本的には星形成時 の光度関数を反映している。 表4は運動特性で分けたグループ毎の相対光度関数である。空間速度と年齢との 強い相関により、このグループは異なる平均年齢を表わしている。表の数字は Mv と |W| または S の組み合わせを持つ星の数で、5.5 ≤ Mv ≤ 7.5, つまり Mv = 6, 7 の数字の和=2となるよう規格化した全光度関数との相対値が載っている。 だから、もし光度関数に年齢効果が無ければ全ての欄は1になるはずである。Mv = 5 の行は進化効果の影響があるようだが、他の欄は1に近い値をしめしており、誕生時の 質量分布が保存されているようだ。 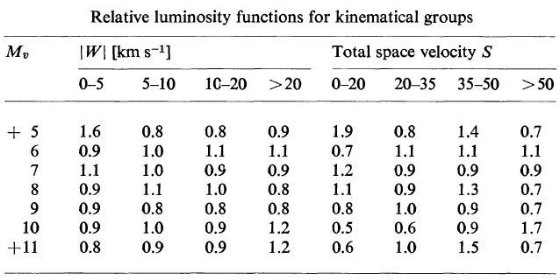 表4.運動特性で分けたグループ毎の相対光度関数。Wは銀河面垂直方向速度。Sは 速度の絶対値。 |
|
B - V グループ分け グリーゼ星の年齢は色等級図の位置や、CaII輝線強度から判る。しかし、 年周視差が精度良く測られて、進化が進んだ星の数は図2から判るように 少ない。したがって、各運動グループの平均年齢を決めることが大事になる。 図2でグループ 1 - 5 と 6a - d は主系列に載っているか、近くにある星を B - V で分けたものである。平均年齢は単純に主系列年齢の半分とした。 グループ 7 は古い巨星を表わす。 運動グループ 図3には、 B - V < 0.50 (F6 より早期型), r ≤ 20 pc のグリーゼ星 の速度分布である。U 軸は銀河中心方向を、V 軸は銀河回転方向を向いている。 空間速度は太陽運動、Uo = +9 km/s, Vo = +12 km/s を補正してある。図3で 最も目立つ特徴は、運動方向偏差 (vertex deviation) である。運動群の徴候は 見えない。表5には速度分散の結果をまとめた。ここにはグリーゼカタログ中の McCormick K+M 矮星を含めた。それらが、太陽近傍で一般的な星の代表と看做 されるからである。表 5 の V☉ は太陽運動の V 成分とグループ 平均運動との差である。速度分散と非対称ドリフトは年齢と共に増加する。 古い巨星と白色矮星の運動は McCormick の K+M 矮星のそれと近い。 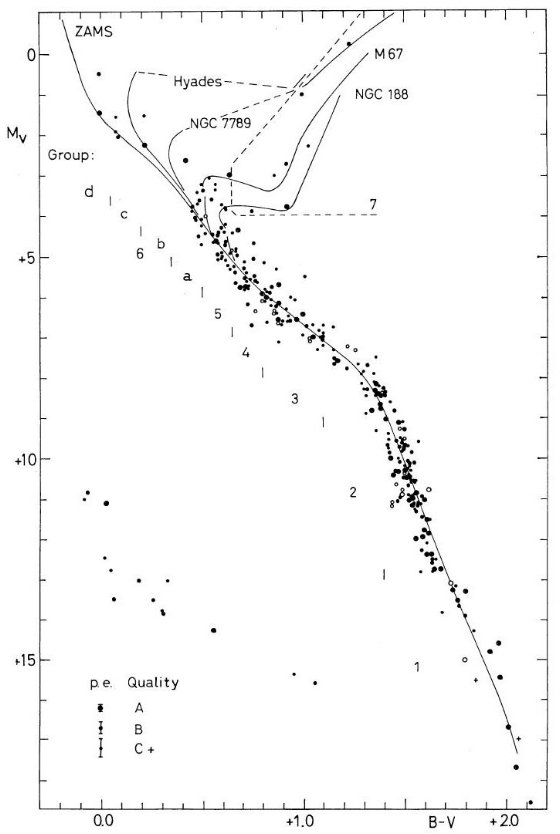 図2.年周視差を持つグリーゼ星の色等級図 |
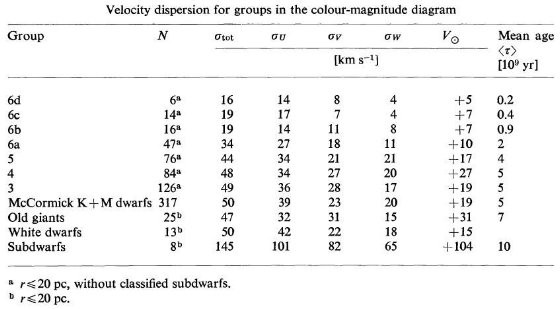 表5.色等級図で分けたグループ毎の速度分散 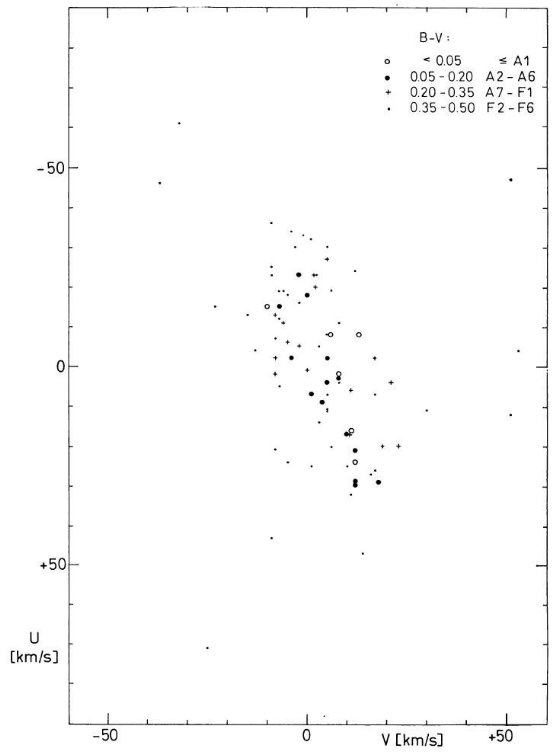 図3.B - V ≤ 0.5, r ≤ 20 pc のグリーゼ星の速度分散。 |
|
速度分散の年齢による増加 図4から速度分散の年齢による増加は、銀河面に平行な成分 U, V でも垂直な 成分 W でも同じことが判る。フィールド星の速度分散は巨大分子雲との遭遇で σ ∝ τ1/3 で増加して行く。これは図4の結果と 一致する。同様の結果は重力波による散乱の数値シミュレーションからも得られ ている。 |
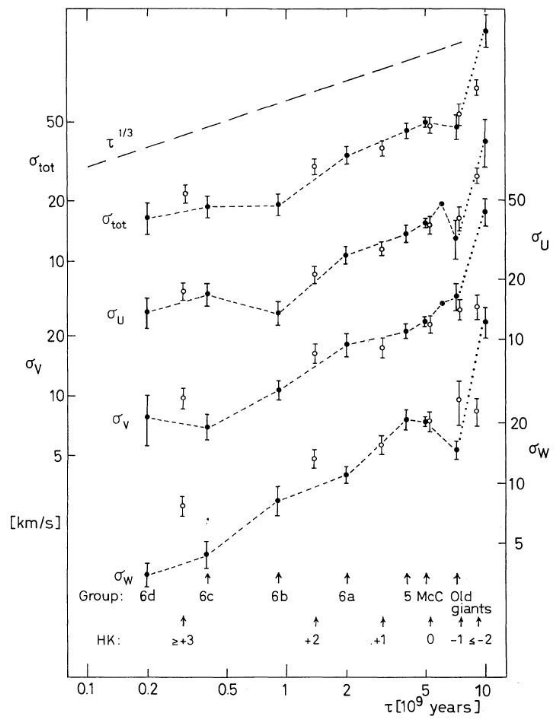 図4.速度分散の年齢変化 |
|
HK 線強度が強いと若い Wilson は HK 線強度を +8(非常に強い)から -5(ない)までに分類した。 表6では、マコ―ミック K + M 矮星に対し、HK 強度が速度分散にどう関係 するかを示している。HK 強度が低下するに連れ、分散は単調に増加していく。 これは HK 強度が年齢と強く相関していることを物語る。したがって、HK 強度 をまだ進化していない晩期型矮星の年齢指標として使用できるだろう。 年齢較正 年齢の較正法には、 (1)第3章でやった星形成率一定として考えた速度分散と年齢の関係を、 HK 強度と年齢の関係に移す。 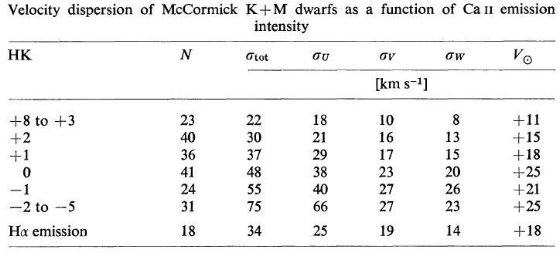 表6.マコ―ミック K + M 矮星の輝線強度と速度分散の関係 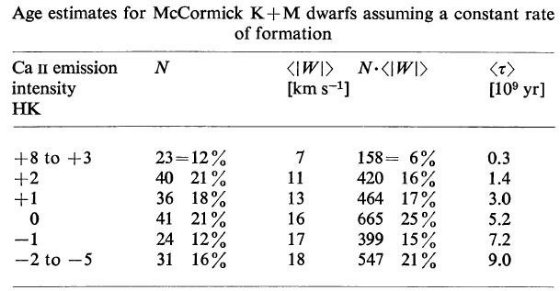 表7.星形成率一定を仮定した K + M 矮星輝線強度と年齢関係 |
(2) HK 強度の累積頻度ダイアグラムを作り、星形成史を仮定して年齢に直す。 表7では星形成率一定の仮定で銀河面に垂直な円筒中の HK 強度に対する年齢を定めた。 星形成は 1010 年間続いたと考えている。円筒内星数の相対値は一定体積内 の星数に |W| を掛けて出した。こうして出した年齢は粗いものであるが、これは σ と τ の関係に驚くほどよく合う。その上、ヒアデス、HK = +3 (Wilson 1966) は等時線フィットからは 0.9 Gyr であり、表7と良く合う。 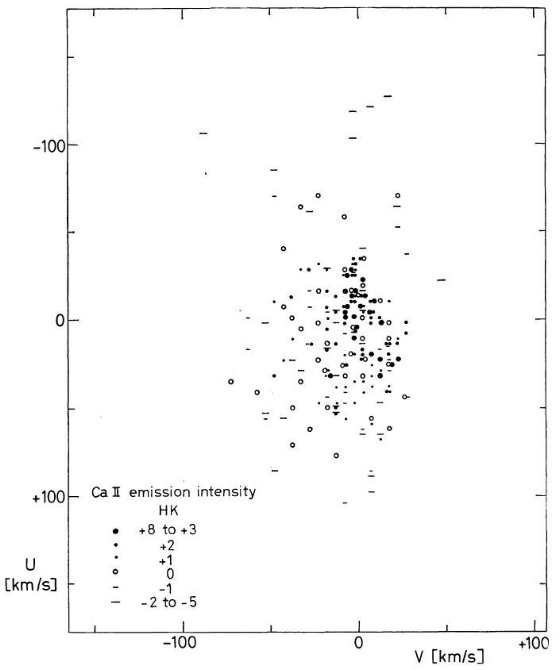 図5.K + M 矮星の HK 輝線強度 と 速度変化 |
|
方向偏差と年齢の関係は最近多くの研究がある。それらは皆方向偏差 ψ が
若い星で大きく、古い星で小さいかゼロになると結論している。しかし、著者らの
データ選択にはその結論に有利になるバイアスが掛かっている。例えば、しばしば
サンプルは軌道離心率が e ≤ 0.15 となる星から選ばれている。しかし、
速度空間でこれは大雑把には軌道楕円の主軸が銀河中心方向を向く領域なのである。 若い星の場合、速度分散が小さいので、ψ ∼ 0 へのバイアスは小さい。 しかし、古い星では分散が大きく、 e ≤ 0.15 で指定されると、仮に 実際には方向偏差が若い星と同じように大きくても ψ ∼ 0となる確率 が上がる。バイアスを避け、同時に低速度の星を選ぶために UV 面内に円形の サンプル領域を設けた:(U2 + V2)1/2 ≤ 40 lm/s, |W| ≤ 15 km/s とした結果を表8に示す。 サンプリングが円形な為に ψ のエラーが大きい。若い星の方向偏差は 確かに大きく 20° に及ぶ。しかし、低速度星の方向偏差が年齢と共に 減少するかどうかははっきりしない。 |
 |
|
マコ―ミック K + M 矮星 グリーゼカタログは全体としては選択効果が効くので近傍星の代表には出来ない。 しかし、その一部のマコ―ミック K + M 矮星は近傍星速度分布を表わすのに 使える。これらは対物プリズム乾板から選ばれている(Vissotsky 1963)ので運動 バイアスはない。そしてそれらは様々な年齢の星の混合物と看做せる。 グリーゼカタログ中のマコ―ミック K + M 矮星の速度分散は表5に示されている。 これらの星の速度分布は良く知られたVの非対称性を持ち、低速度で強い方向偏差 を示す。 |W| 対 σU, σV 関係 マコ―ミック K + M 矮星を |W| 別に分けると、|W| が大きくなると σU, σV も増加することが表9から判る。 表9には到達平均光度も示した。σU, σV の増加は年齢効果であろう。 |
銀河面に垂直な筒中の速度分布 銀河面に垂直な筒中の速度分布を得るにはどうしたらよいだろう?滞在時間 の逆数で重みを付ければよいから、|W| の重みで速度分布を求めればほぼ正しい。 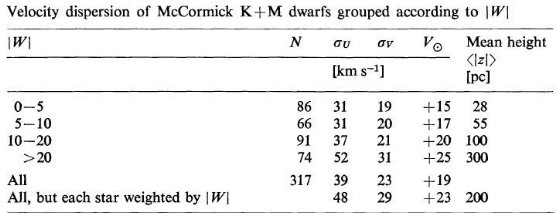 表9.マコ―ミック K + M 矮星の |W| 別の速度分散 |
|
|
|

|
|
|

|
|
|

|
|
|
