| Parker, Humphreys 2003 で見つかった厚い円盤/ハローの非対称性に伴う運動学的な特徴を報告する。 同一のカラーと等級基準で選んだ 741 星の視線速度を観測した。対象星は 非対称性が見出された領域とそれに対応する第4象限の比較域に属している。 我々は視線速度、スペクトル型、メタル量を求めた。我々は二つの領域の間で VLSR 分布の非対称を見出したばかりでなく、第1象限の星の 角速度 ω は、それらの有効角速度が第4象限に較べ遅いことも見出した。 VLSR と ω には銀経 l に対する興味深い依存性があり、 それは第1象限で最も著しい。[Fe/H] 測定結果から星を3つのグループ、 ハロー、厚い円盤、薄い円盤に分けると、厚い円盤の星が第1象限では遅い回転 速度を示す。 | 厚い円盤の星は観測された VLSR と ω の銀経 依存性を生み出す原因にもなっていた。 VLSR の動径、横向き(?)、 銀河面に垂直方向成分から、第1象限の厚い円盤星は銀河回転方向に 800 - 90 km/s の遅れがあることが判った。一方、第4象限の星は 20 km/s の遅れしか 示さない。これは二つの方向間での運動学的非対称性である。 Parker, Humphreys, Larsen 2003 では、星計数の非対称性は3軸不等の厚い円盤か、薄い円盤中のバーと厚い円盤 /ハロー星との相互作用のどちらでも説明可能と述べた。今回の結果は、バーとの 重力相互作用により生じた厚い円盤の回転遅れが、星計数と運動特性の非対称性 の原因であることを示す。しかし、最近発見された大犬座ストリームか類似の マージャーデブリと関係するかも知れない。 |
|
非対称の発見 Parker, Humphreys, Larsen 2003 は中銀緯帯での星計数が銀河系の南北に関し非対称であることを見出した。 3軸不等の厚い円盤 3軸不等の厚い円盤は薄い円盤とは明白に異なる回転速度を持つであろう。 実際、Reid 1998, Beers, Chiba 2000 は厚い円盤星が、薄い円盤に較べ 30 - 50 km/s の遅れを持つことを示した。 |
回転バーとの相互作用 銀河系中心から 3 - 4 kpc で共回転する円盤内の高速回転バーは重力ウェイク を引き起こし、それがバーの後方に星を捕えてため込むだろう(Hernquist, Weinberg 1992, Debattista, Sellwood 1998)。 バーに反応して、星の超過だけ でなく、回転速度の遅れも見られるであろう。 運動による原因の特定 どちらの場合でも、構造特性を反映する運動特性が観測される筈である。 |

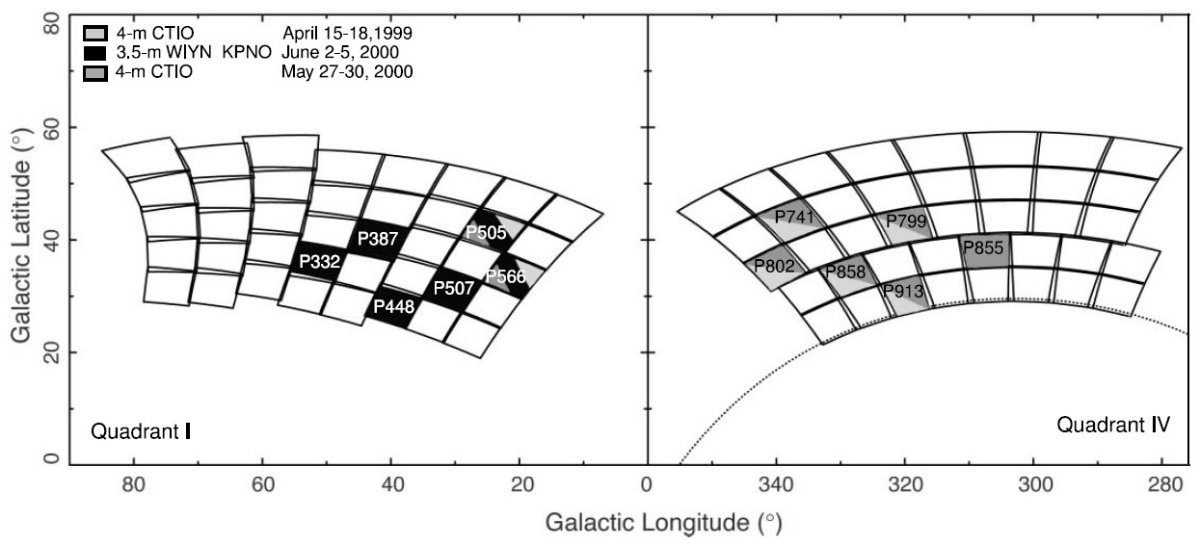
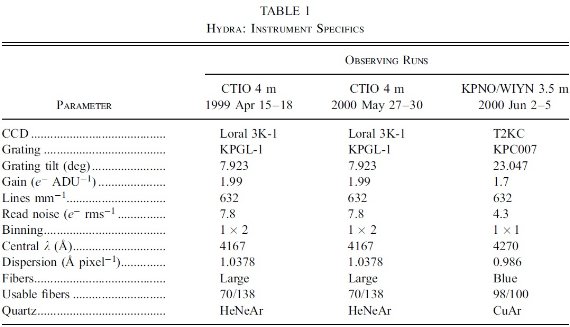 表1.HYDRA の諸元。 観測装置 観測には CTIO 4m BLANCO望遠鏡と KPNO WYNN 3.5 m 望遠鏡の他天体分光器 HYDRA を使用した。WYNN HYDRA は視野角 1° で 3000 - 7000 A のスペクトルを 98/100 星に対して取得した。CTIO HYDRA は視野角 40′ で 3000 - 11000 A のスペクトルを 70/138 星に対して取得した。どちらも分解能は 1 A である。 星の選択 対象星は第1象限の星超過が強い4領域と二つの渡過域、それに第4象限の それらの比較領域が選ばれた。図1にはそれらの分布を示す。O = 16 - 18 mag で、カラー (O-E) は (O-E)peak と [(O-E)peak -1] の間の星をランダムに選んだ。この条件だとハロー/厚い円盤の星の割合は 80 % を越えていると期待される。 |
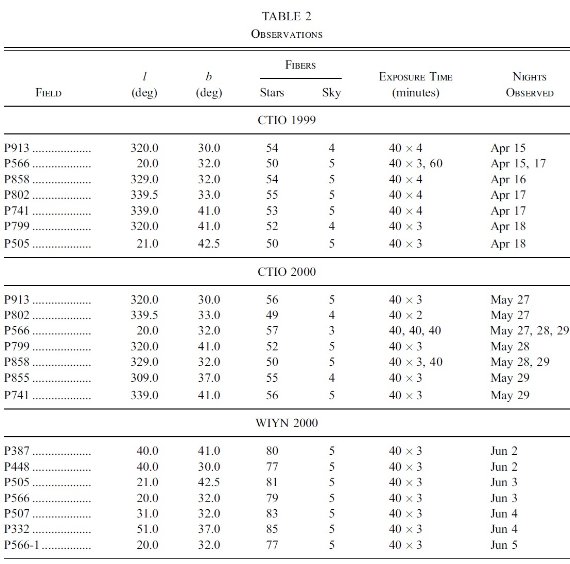 表2.観測記録 フィールドの情報 表2には観測したフィールドの情報を載せた。 |
| データ整約は IRAF/DOHYDRA で行った。約 1000 個のスペクトルをこのソフトで 処理した。視線速度は IRAF/RVIDLINES で求めた。最終結果として、 741 星、内 418 は第1象限、 323 は第4象限の視線速度を求めた。表4に 太陽中心速度を示す。 |
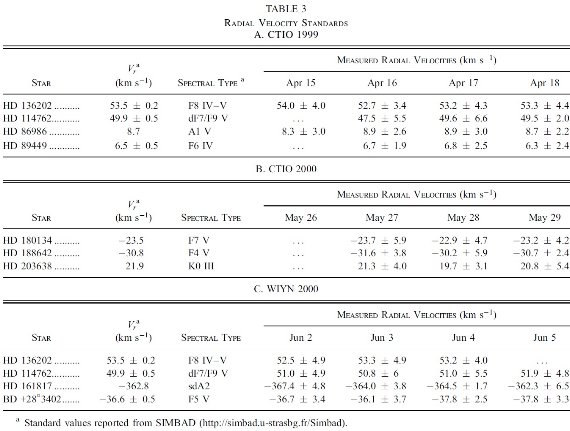 表3.視線速度標準星 |
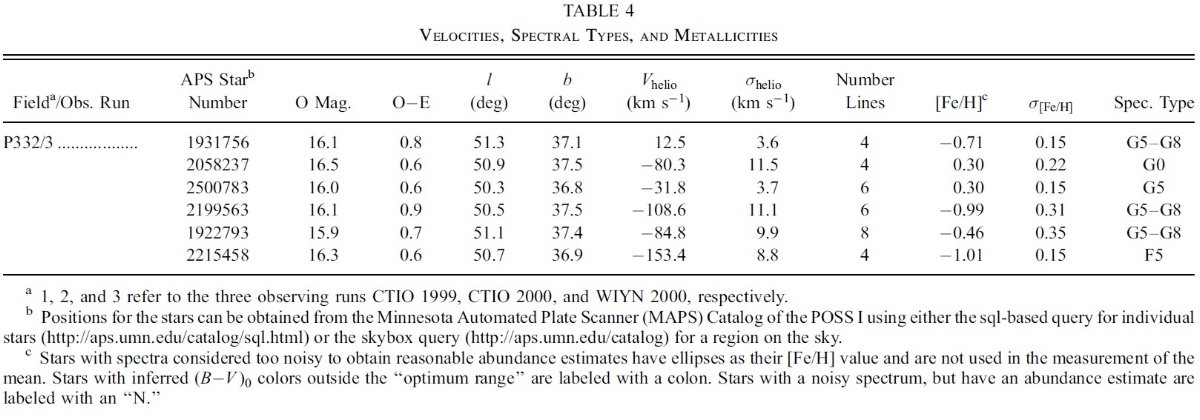
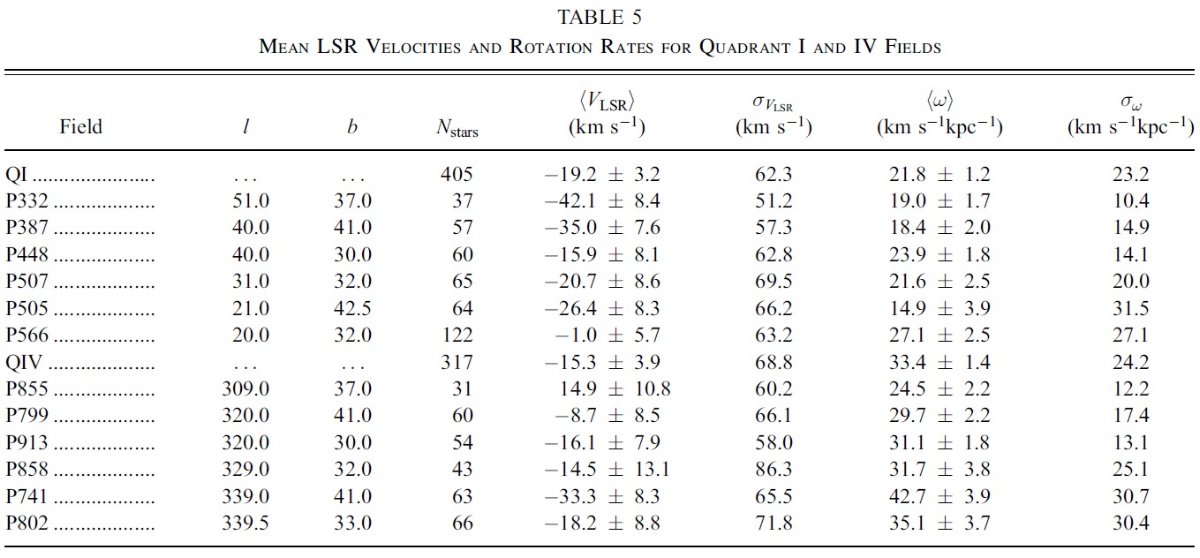
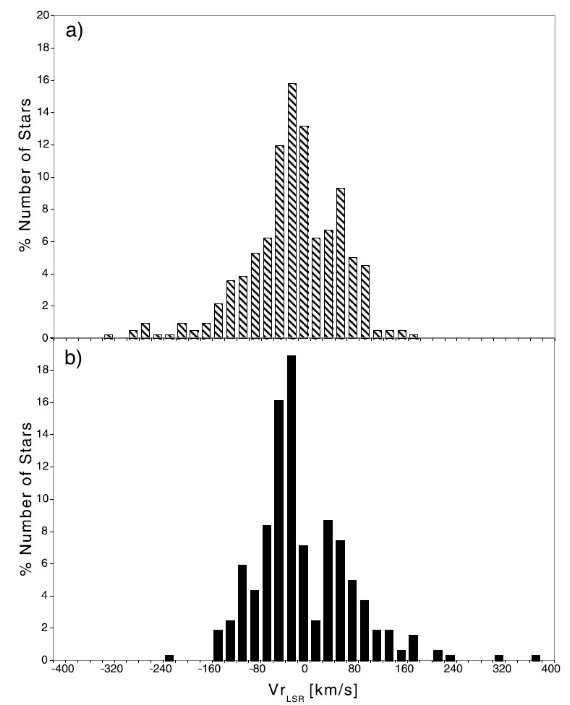 図2.LSR 速度の規格化分布。(a) 第1象限 (b) 第4象限 4.1.運動特性視線速度が負?図2に LSR 速度の規格化分布を示す。図2(a) 第1象限が負速度側に尾を引き、 図2(b) 第4象限が正速度側に尾を引くのは期待通りだが、驚いたことに どちらもネットでは負速度である。明らかに種族II の視線速度が ± 200 km/s を越す星を除いた後の平均 LSR 視線速度は第1象限で -19.3±3.2 km/s, 第4象限で -15.3±4.0 km/s である。標準偏差は σ = 65.3 km/s と 68.8 km/s である。 なぜ? もし軸対称の厚い円盤が薄い円盤と同じくらいの速度で円回転していると 仮定すると、LSR で動いている観測者からは第1象限の星は正、第4象限の星 は負の視線速度で観測されるだろう。しかし、厚い円盤は薄い円盤より約 30 - 50 km/s 遅い速度で回転していることが知られている。したがって、厚い円盤 の視線速度は第1象限では負方向に、第4象限では正方向にずれるはずである。 勿論サンプルには薄い円盤、厚い円盤、ハローの星が混ざり合っている。しかし 予想された円盤速度 10 - 25 km/s に対して、観測速度はずっと大きくずれて いる。これは二つの象限の星の間で運動に非対称性が存在する証拠である。 おそらく、速度の遅れがもっと大きく、異なる運動をする星種族が存在するので あろう。 |
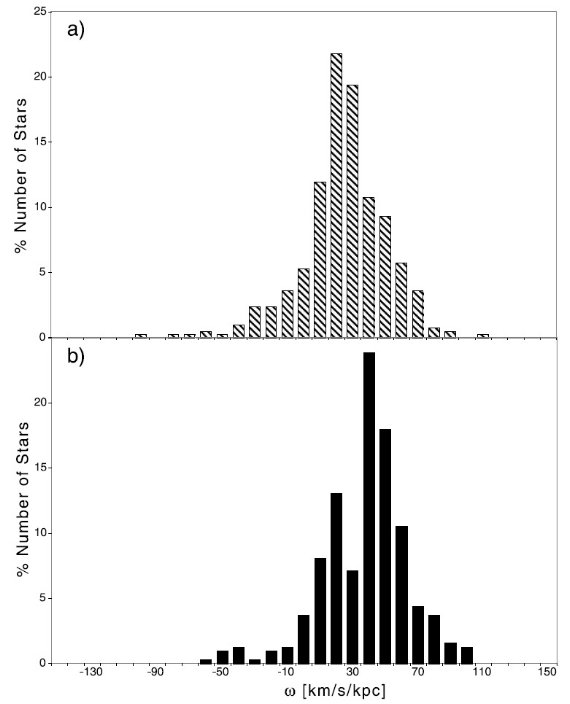 図3.回転速度の規格化分布。(a) 第1象限 (b) 第4象限 回転率の非対称性 ωo = 27.5 km/s/kpc, ωs = 個々星の回転速度、 Ro = 8 kpc, Vo = 220 km/s とすると、 VLSR = (ωs - ωo) Ro sin l cos b この式を使って、求めた個々星の回転率 &omega:s のヒストグラム 図3には、回転率のシフトが現れている。それは第1象限の星と第4象限の星とで 運動特性が異なることを示している。この方向で、太陽から 1 - 2 kpc の距離 だと、銀河中心距離は 6.4 - 7. 5 kpc となる。Brand, Blitz 1993 の近似式を 使うと、そのあたりの銀河系回転率は,ω = 30 - 38 km/s/kpc である。 高速度星を除去したサンプルでの回転率を求めると、第4象限では ωs = 33.4±1.4 km/s/kpc となり、予想と一致する。 しかし、 第1象限での平均値は、 ωs = 21.8±1.2 km/s/kpc で 低い回転速度を示している。 絞込みにはまだ不足 しかしながら、これらの情報だけでは、厚い3軸円盤の主軸に沿った星流の効果 と回転の遅れとを区別することはできない。しかし、表5にある個々の区分域での 視線速度を見ると、興味深いことに、 銀経が大きくなるほど VLSR は より負方向に動くことが判る。この傾向は二つの仮説の間を区別するのに使えるかも 知れない。 |
4.2.スペクトル型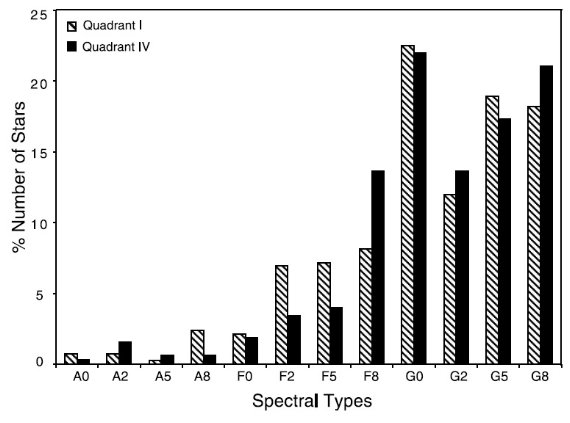 図4.第1象限と第4象限でのスペクトル型の分布。 スペクトル型の決定は「近似的」である。主に Jones 1996 ftp://ftp.noao.edu/catalogs/coudelib を用いて行った。大体、低メタル星の標準スペクトルが少ない。 図4を見ると、第1象限と第4象限とでは大体同じ割合でスペクトル型が 分布しているようである。 |
4.3.メタル量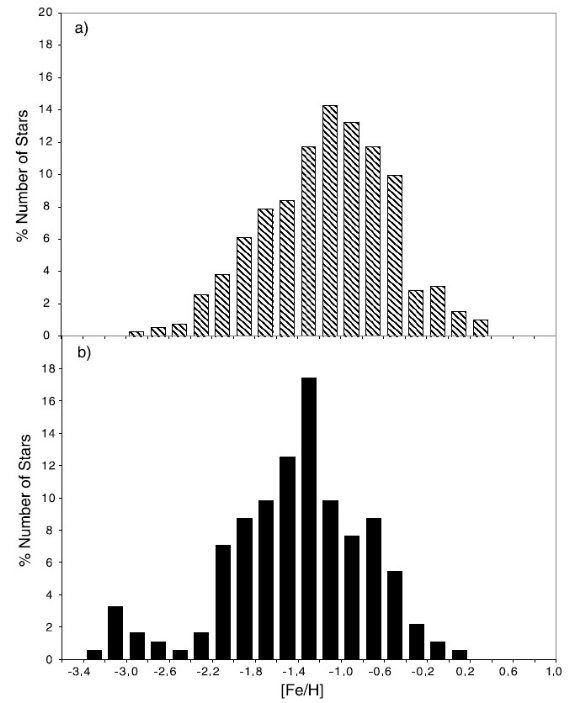 図6.メタル量の分布。(a) 第1象限 平均 [Fe/H] = -1.06。 (b) 第4象限 平均 [Fe/H] = -1.27。 メタル量の評価には Beers et al 1999 の方法を用いた。それは Ca II K 線 指数 KP と (B-V)o カラーとの関係に基づいている。ただし、我々は (B-V)o を持っていなかったので, 代わりにバルマー線指数 HP2 を使った。 この方法で我々は 581/741 星のメタル量を決定した。図6にあるように、 第1象限サンプルは第4象限より少し高メタルである。 |
|
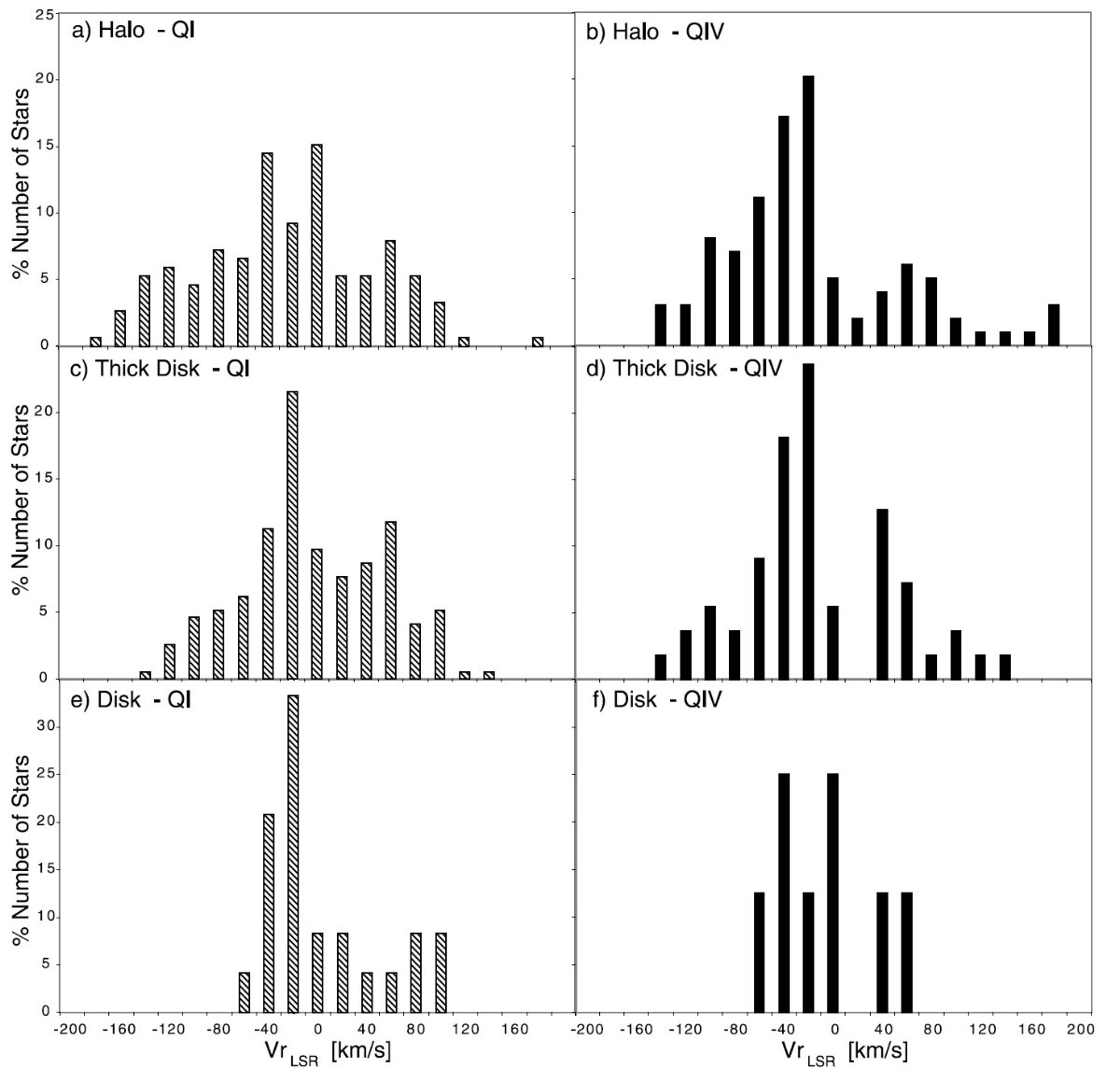
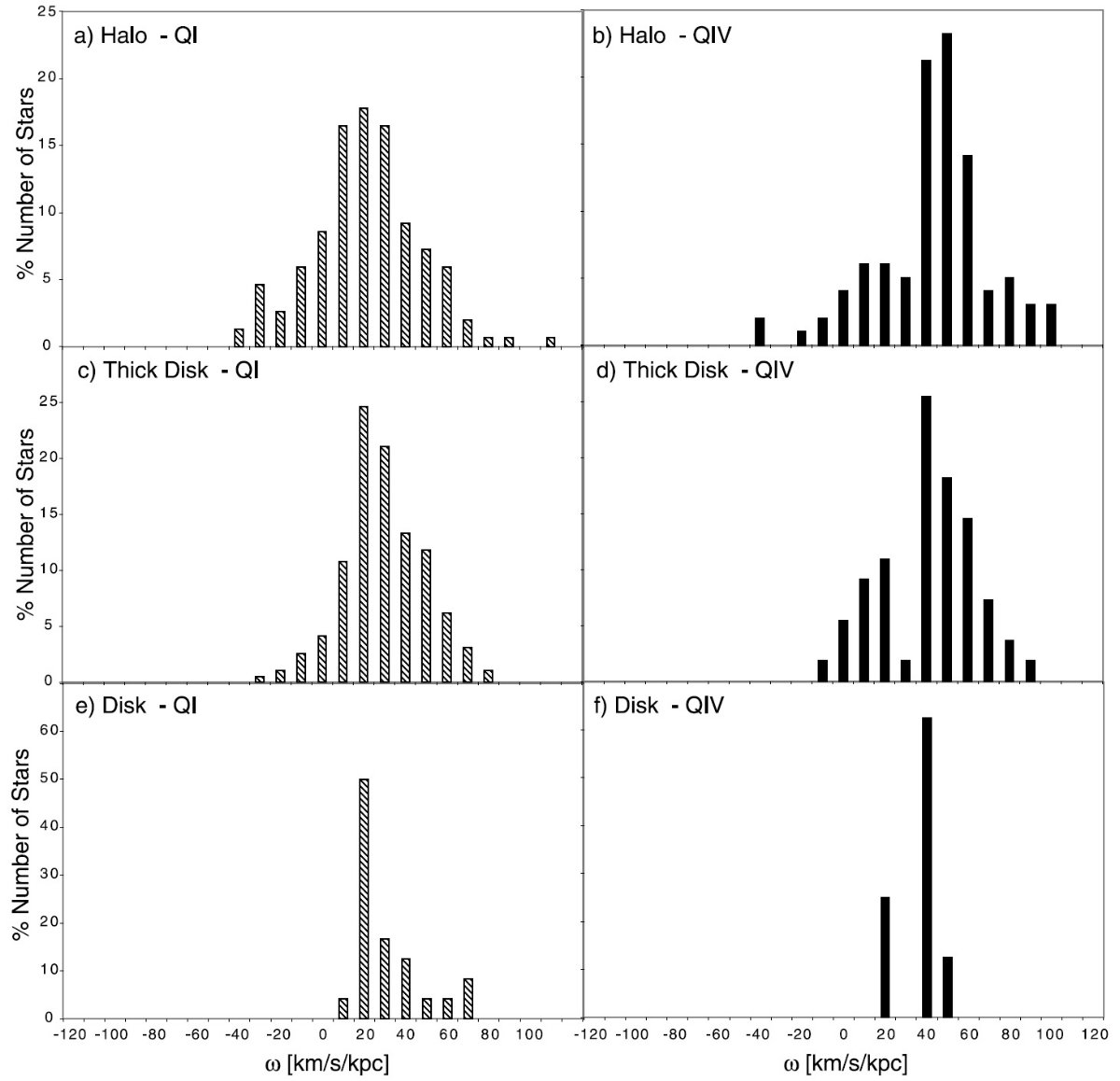
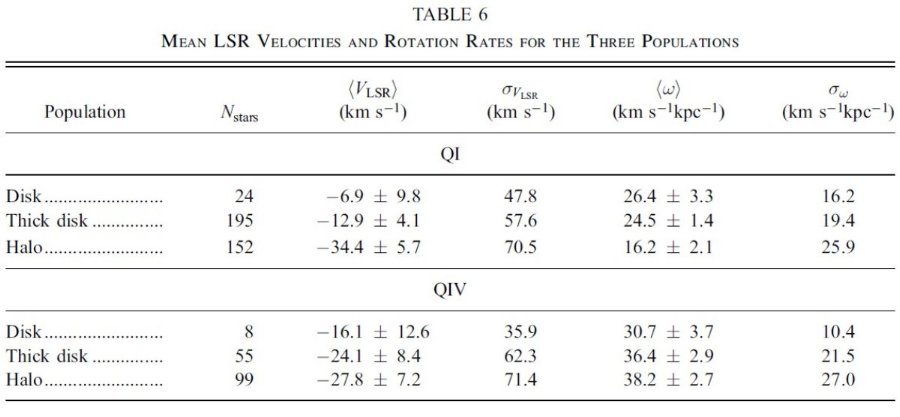
VLSR と [Fe/H] による種族分離 薄い円盤 [Fe/H] = [-0.3, 0.3] 厚い円盤 [Fe/H] = [-1.2, -0.3] ハロー [Fe/H] = [-2.2, -1.2 ] しかし、|VLSR| ≥ 150 km/s ならばハローに再分類と言うチューニングは 行う。表6に、その結果を示す。図7と図8には結果をヒストグラムにして示した。 ハロー ハロー種族の VLSR 分布は大きな散布度が特徴である。このため 二つの象限の結果を区別することができない。第1象限の回転角速度は第4象 限より僅かに小さいようである。 厚い円盤と薄い円盤 厚い円盤と薄い円盤では二つの象限の間の差は、第1象限の星は第4象限より ゆっくり回っているという以前の結論を確認するものである。期待されていた VLSR は、第1象限では正、第4象限では負であったことを思い出 して欲しい。その方向と距離では、その値は 10 - 25 km/s 程度であった。 第4象限の薄い円盤と厚い円盤の平均 VLSR は予測とほぼ一致する 値であった。ただし、厚い円盤の星は第4象限では VLSR が正方向 に大きくずれる、つまりもっとゆっくり回転するというこの種族に期待された 傾向は示さなかった。第1象限ではもっと負方向にずれるという現象がはっきり 示された。これは第1象限と第4象限の間での運動学的な非対称性を明白に示す 結果である。 速度分散が大きい理由 厚い円盤では両象限で、また薄い円盤では第1象限で速度分散が、厚い円盤の 通常の値 45 km/s、薄い円盤の G-型主系列星の 30 km/s より大きな値である ことも注目すべきである。これは他の種族の混入の結果である可能性が高い。 |
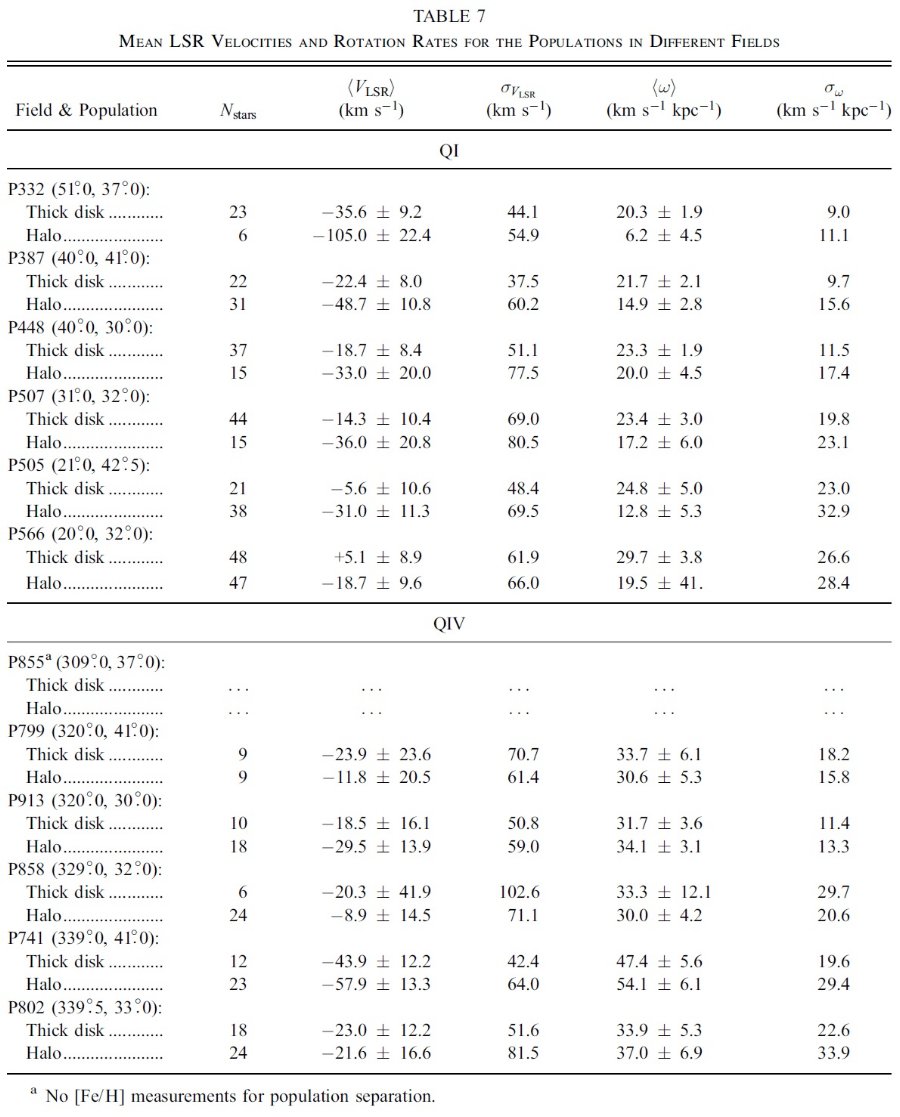
VLSR に銀経による勾配がある 4.1.節で VLSR に銀経による勾配があることを指摘した。 [Fe/H] と言う新しい情報を得て、種族別に VLSR と ω の 変化を調べ、表7にまとめた。第1象限の厚い円盤星、それとある程度まで だがハロー星は VLSR に銀緯依存性を示す。これに対し、第4 象限星はそのような傾向を見せない。 vr, vφ, vz を最少二乗フィットで決める 星の速度成分 vr, vφ, vz は星の位置に応じて、それぞれ VLSR への寄与度が異なる。例えば l = 20 では、 vr が重要だし、 l = 40 - 50 では vr と vφ が同じ くらい寄与する。異なる領域の間で星種族が一様であると仮定すると、銀経依存 から、速度の3成分を分離して評価できるだろう。 (vr, vφ, vz が場所に依らないという意味? ここまでは VLSR は vφ が決めているという前提 で解釈していたようだったが?)
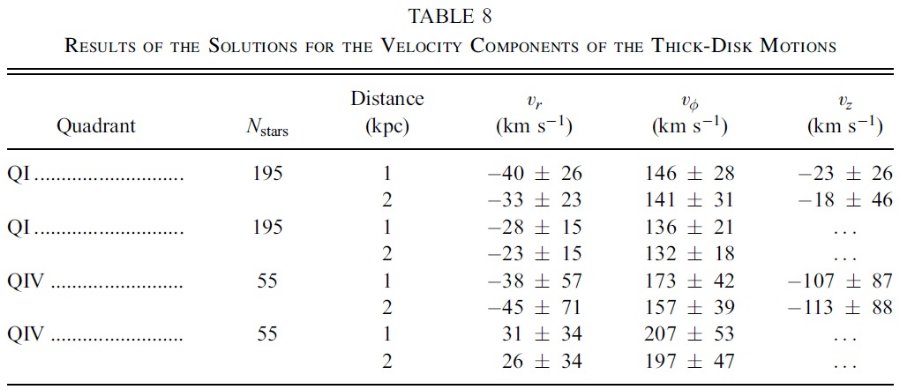
ここに、θ = 太陽から星への視線と銀河中心から星への線のなす角度で、 Rs は銀河中心と星との距離、 sin θ = Ro sin l /Rs である。星までの距離を 1 - 2 kpc と仮定して、上式を最少二乗フィットして vr, vφ, vz を求めた。その結果を表8に示す。驚くべきことではないが、 解の不定性は非常に大きい。そうではあるが、解は第1象限星の vφ が銀河円周回転速度より 80 km/s 遅く厚く、厚い円盤に想定される回転方向 速度よりも 40 - 50 km/s 遅れていることを示す。動径方向速度成分は銀河中心方向に 落ち込んでいるが誤差を考えると有意とは言えない。同じことを第4象限の星に 対しても行った。サンプル数が 55 と少ないが、結果は第1象限とはっきりと 異なる。vz は非常に大きな値を示し、多分意味がないので、 vz = 0 と仮定した場合も計算した。 結論として、第1象限の厚い円盤星は銀河回転速度に 80 - 90 km/s の遅れを 有し、一方第4象限の星は遅れが僅か 20 km/s である。この差が運動特性の 非対称性の表われなのである。 |
|
マージャーの残余構造 ありそうにないと結論済み。 バーと OLR 銀河面内の恒星バーの存在は、 Weinberg 1992 Lopez-Corredoira et al 1999, Feast, Whitelock 2000 Hammersley et al 2000 はバルジを越えた先、半径 3 - 5 kpc まで伸びた恒星バーの存在を明らかに した。 Weinberg 1994 は円盤上に回転する構造が3つの共鳴点、内側と外側リンドブラッド共鳴 (OLR), 共回転、を持ち、速度分布に著しい特徴を生み出すことを示した。 彼のモデルでは、3軸バルジは銀河中心から 4 - 5 kpc 離れた OLR 付近で 著しい速度分散を生み出す。我々の観測で見出された大きな速度分散はこの OLR 現象かも知れない。しかし、バーの角運動量ロスが速度分散を生み出す 可能性もあり、 Weinberg 1994 自身はそれの方がありそうと考えている。 |
デブリ Martin et al 2004 は Canis Majoris マージャー残存構造の発見を報告した。 それは銀河面に比較的近い。これが我々の非対称性に影響している可能性もある。 |