Detection of a Large Scale Stellar Bar in the Milky Way

　アブストラクト

　１．イントロダクション　

　２．天体選択　

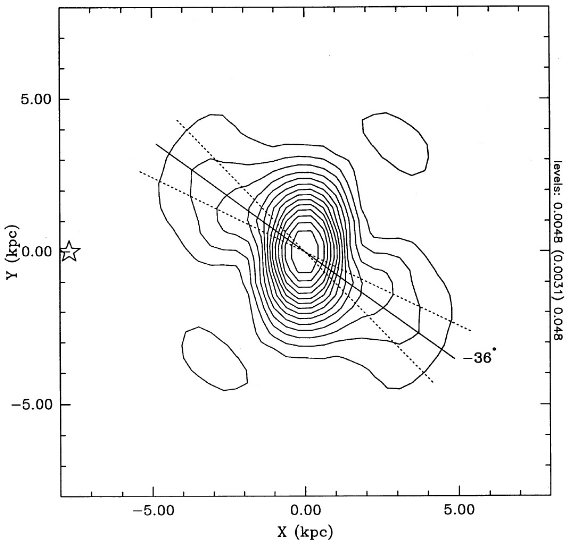
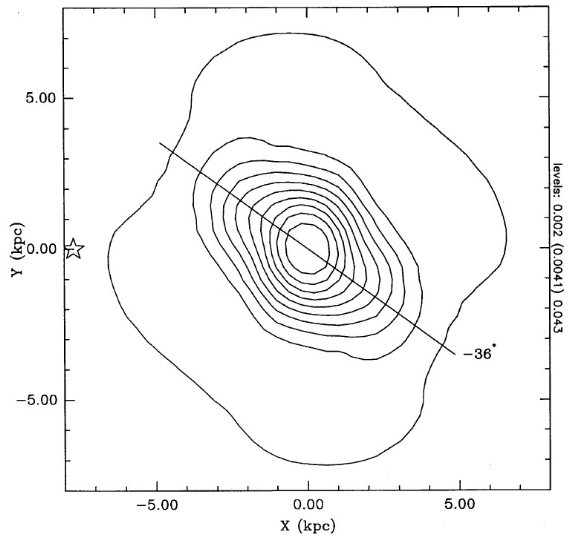
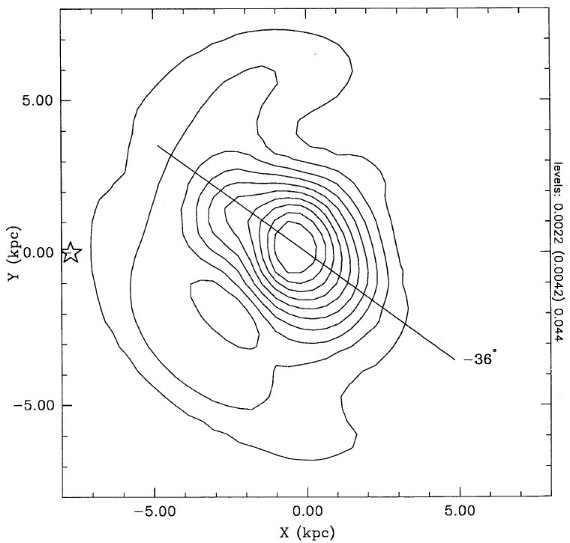
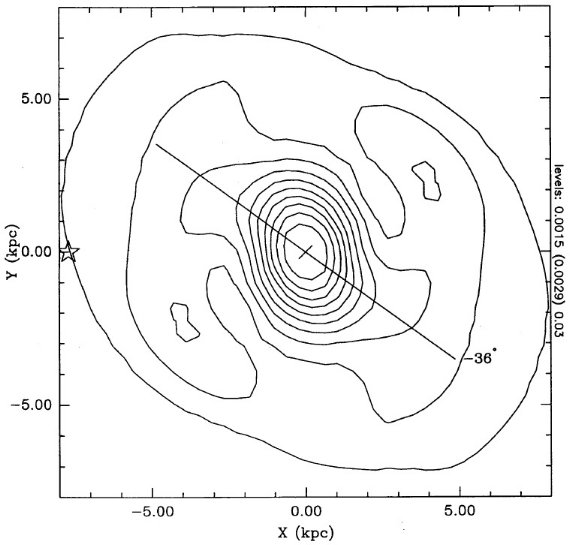
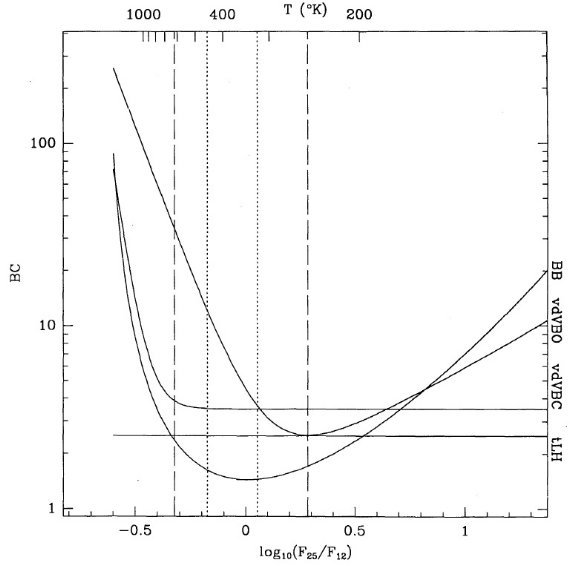
サンプルの選択　 　追跡天体を選ぶためには一様性が重要である。IRAS PSC から変光 AGB 星を 選ぶ。そのためにフラッグ VAR を使用する。問題点が二つある。 （１）観測回数が場所により違う。 （２）コンフュージョン。 これらを避けるため、次の制限を設けた。 （１）F12 > 2 Jy　　　38,004/158,000 12μm 検出 （２）VAR > 98 %　　　　 5736/38,004 （３）|b| < 3　　　　　　3170/5736 98 % は 12, 25 で検出。F60/F25 > 1 の 143 は星形成域天体 であろうが、 全体の 5 % なので無視する。またそれらは天空上を 等方的に分布している。 　サンプルのカラー　 　図１にカラー C = log10(F25/F12) の分布を示す。ピークは C = -0.12 にある。そのカラー温度 = 380 K である。最も青い区分は C < -0.174, 最も青い区分は C > 0.053 である。

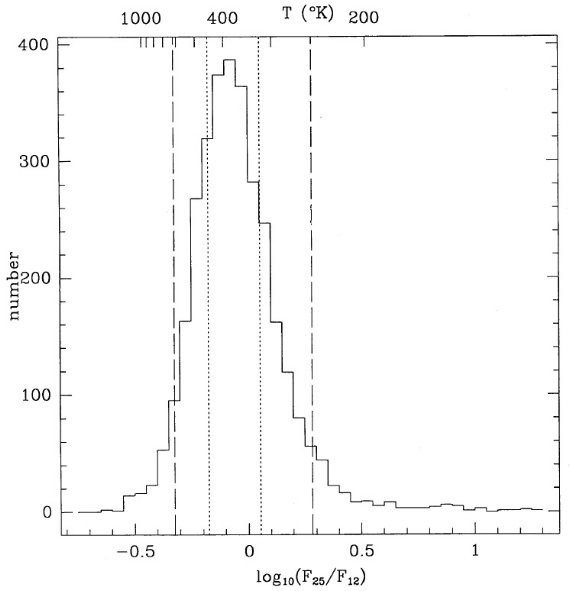
図１．IRAS PSC から選んだ 3170 天体の C = log10(F25/F12) 分布。 点線は最少４分線(C < -0.174)と最大４分線(C > 0.053。 破線は 90 % の境界線。

　３．マップ方法　

３．１．測光距離　 　１．固有光度を決める　 　仮定として、前章で選んだ天体は分散ゼロの一定光度を持つと考える。バル ジの OH/IR 星は平均光度 8 103 Lo で、散布度は距離の違いのみ で期待される大きさに過ぎない (te Linkel Hekkert 1990). Claussen et al. 1987 は炭素星のフラックス限界サンプルを調べ、その光度を 3 103 Lo - 4 104 Lo としたが、平均値は 8 103 Lo で、 標準偏差は 1 103 Lo であった。このように OH/IR 星は 炭素星と同じくらいの光度を持つようである。IRAS 変光星を OH/IR 星と 炭素星の集合と考えると全体のっ標準偏差は Claussen et al. 1987 の図５から判断して 0.5 等以下であろう。平均光度のエラーは距離の スケールを変えるだけなので容易に修正可能である。散布度の影響に関して 言うと、0.5 等以下ならこれから述べる結論に影響しない。１等になると 全体の形態は同じだが少し歪みが生じる程度である。このように、赤外で 明るい AGB 星 = IRAS 天体の光度散布度は標準光源と見なせるほどに 狭い。 　２．輻射補正　 　図２から分かるように、O-リッチと C-リッチな AGB 星では SED が異なる。 様々なグループの星に対し BC が提案されてきた。この論文では、 C = log10(F25/F12) の黒体輻射に対する輻射補正を採用する。 　３．減光補正　 　A12 = k(mag/kpc) d(kpc) と考える。銀河中心　d = 8 kpc で Av = 30 mag, A12 = Av/15 - Av/20 と考えると、 k = 0.18 - 0.24 mag/kpc である。

図２．輻射補正のカラー指数 C による変化。BB = 黒体輻射への 補正。vdVBO = van der Veen, Breukers O-リッチ星。 vdVBC = van der Veen, Breukers C-リッチ星。tLH = te Lintel Hekkert の輻射補正。

　３．２．フーリエ法　

　４．結果　

　４．１．ＢＢ輻射補正一定によるモデル　

密度ピーク距離　 　減光率として A12 = 0.21 mag/kpc を採用した。これを 0.16 mag/kpc にすると中央密度ピークの距離が 8kpc となった。この一致は 方法が大体良いことを示している。 　スタートサンプル　 　初めは C > 0.053 の最も赤い 793 天体を第３章の方法で処理した。 この範囲は te Lintel Hekkert 1990 が多数のバルジ OH/IR 星を発見 した領域である。密度分布を求める際には A12 = 0.16 mag/kpc を 使用した。 図３．C > 0.053 サンプルの分布。目盛は kpc. 太陽は (X, Y) = (0, 0)、 銀河中心は (8, 0) である。等高線はピークの 5 % から 100 % まで等間隔。 である。

分布の特徴　 （１）中心集中が高く、比較的軸対称である。 （２）一本腕が方位角 -30° 方向に伸びる。向こう側が見えないため？ 向こう側の構造　 　図３では片側のみに噴き出るジェットに見える。向こう側に距離を伸ばすため、 フラックス限界を 2 Jy から 1 Jy に下げて同じ解析を行った結果が図４である。 明らかに向こう側にも少し弱い腕が見える。これはサンプルの不完全性が原因 であろう。 図４．F12 ≥ 1 Jy, C > 0.053 サンプルの分布図。 ピークの 5 % から 100 % まで 10 % 刻み。

図５．図３と似ているが、サンプルが抜けている方向を ３．２．節の方法で埋 めた。等高線間隔は図３と同じ。 　m = 0 項補正の分布図　 　図５にはサンプルが抜けている方向を ３．２．節の方法で埋めた時の分布図 を示す。図２（３の間違い？）と図５を比べると、全体の構造は変わらない。

図６．偶数次調和項のみで構成した銀河中心周りの分布図。 10 & から 100 % までを等間隔の等高線を引いた。実線＝位置角 - 36°。点線＝位置角 -26°, -46°。 m = 0, 2, 4 項による合成分布　 　図６には、m = 0, 2, 6 の項のみから作った分布を示す。現れたバー構造は 系外銀河のバー構造とよく似ている。バーの長さは 5 kpc で位置角は -36 で ある。角度と長さについて、3.8 , 5.4 kpc, 24°, 46° と色々な数値が 出てくるが理解できなかった。

図７a．m = 0, 2, 4 を使った、表面密度。(図６との違いがよく分からない)

図７b．偶数、奇数次項を合わせた m = 4 までの分布。

　４．１．２．全てのカラー　

全てのカラー C　 　図８には全てのカラー C を用いた分布図を示す。我々は腕の青い種族と バーの古い種族の二つが混ざった構造を見ているのかも知れない。また カラーが光度と関係している可能性もある。特に青い天体では。 　種族の特定が必要　 　種族を特定する必要がある。 　リング？　 　図には渦状腕またはリングに見える構造が存在する。これは人為的な現象では ないだろう。これは Sanders 1984 が述べた 5 kpc 分子リング (Ro = 8 kpc) に 対応するのかも知れない。

図８．図５と同じだが、全てのカラーを用いた。実線＝方位角 -36°.

　４．２．他の輻射補正を使ったモデル　

　５．まとめ