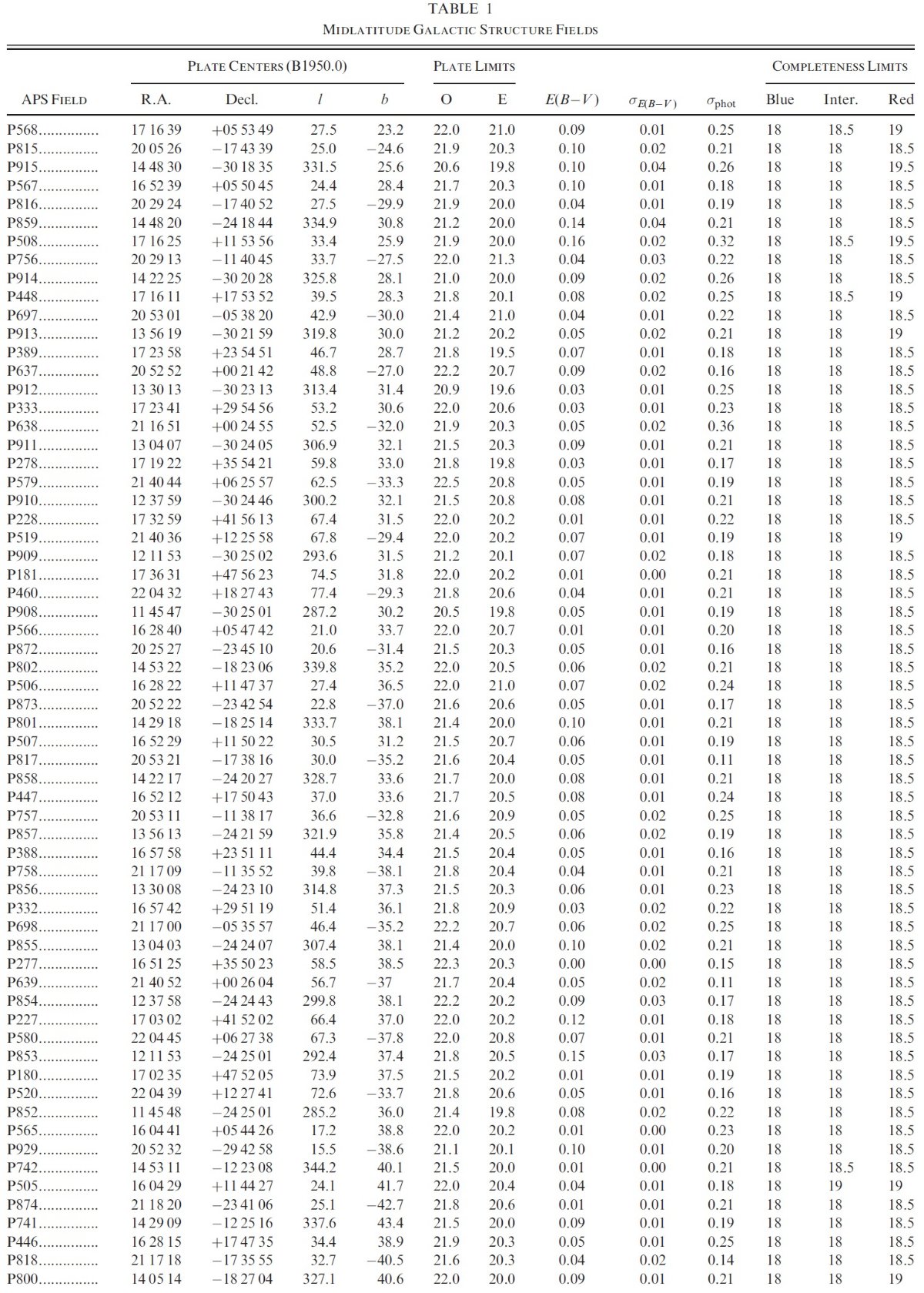
| 厚い円盤と多分内側ハローの太陽から 1 - 2.5 kpc 内側の恒星分布に統計的に有意な 非対称性が存在する。 第1象限では銀河面の上下それぞれで40領域、第4象限で銀河面の上側40の補助領域 で計120の POSS I 領域を比べた。第1象限に、青から中間カラーの星数で 20 & - 25 % の超過を示す広がった領域を見出した。非対称分布を示す領域の形はやや不規則である。 | しかし、超過領域はかなり一様で、数百平方度に渡っている。したがってそれは厚い円盤 や内側ハローの小さな密度揺らぎを越えた大きな構造である。この論文では、 観測と、星計数の結果とその統計的解析を示す。超過の原因としては、(1)マージャーの 残存構造、(2)3軸不等の厚い円盤またはハロー、(3)厚い円盤・ハローが円盤内の バーと相互作用した結果が考えられる。 |
|
POSS I 領域における超過の発見 Larsen, Humphreys 1996 は POSS I の Automated Plate Scanner (APS) カタログから、b = 30 - 40 で4つの対となる各 16 deg2 領域を 選び出し、星計数を行った。彼らは第1象限 l = 20 - 40 にある4領域全てで、 暗くて青い星の数に、l = 0 面に関して逆側と較べ 30 % の超過を見出した。 半中心方向ではそのような超過は認められなかった。彼らの結論はこの超過が 内側ハローまたは厚い円盤は3軸不等形状をしているか、厚い円盤と薄い円盤内 の恒星バーとの相互作用によるというものであった。 |
超過領域の広がりの決定 我々は、|l| = [25, 85], b = [15, 55] の 40(x2) POS I 領域で星計数を行った。 その結果、 超過領域が l = [20, 55], b= [25, 45] の 700 deg2 を越す 領域に広がっていることが判った。銀河面の下の領域 l = 25 - 80 にも探索を広げた 結果、こちら側にも同様の非対称性が見つかった。 |

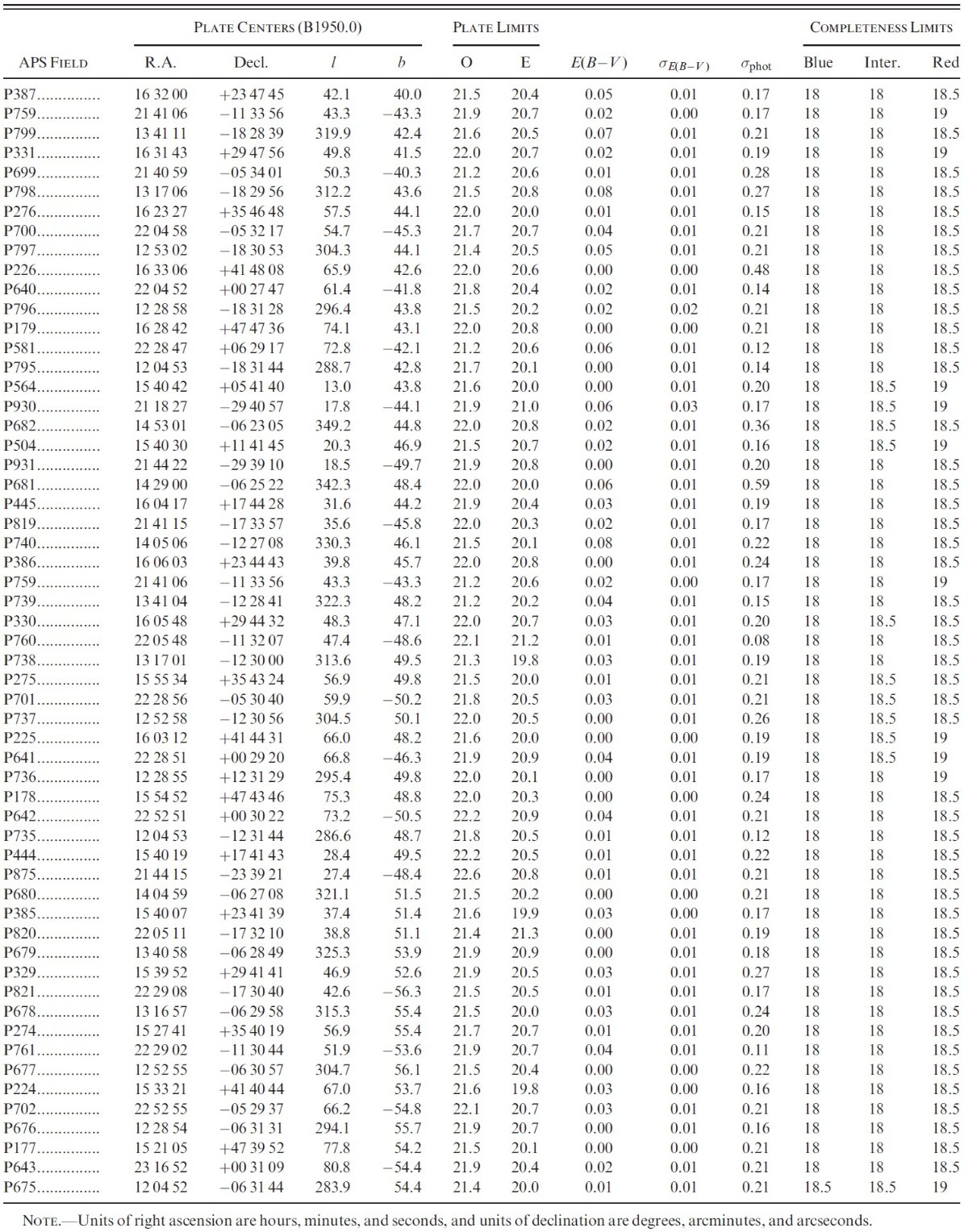
2.観測データ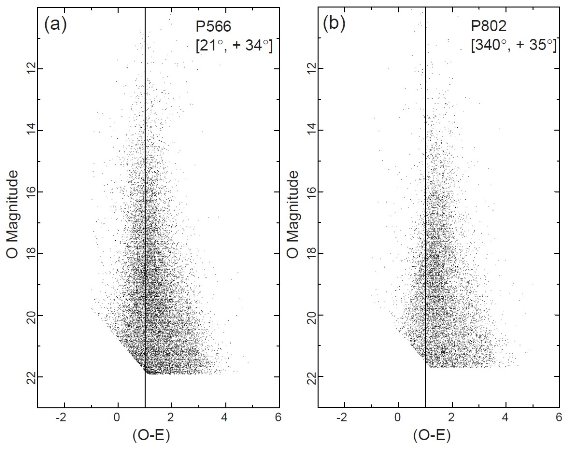 図1.CMD 例。左:P566(21°, +34°) 右:(-20°, +35°) |
3.星計数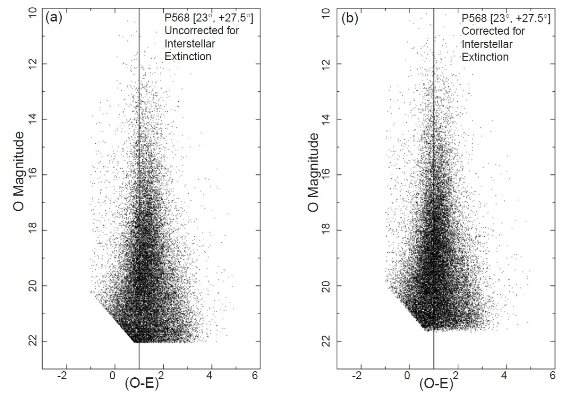 図3.P568(23°, +27°)減光補正の例。左:補正前。右:減光補正後 |
|
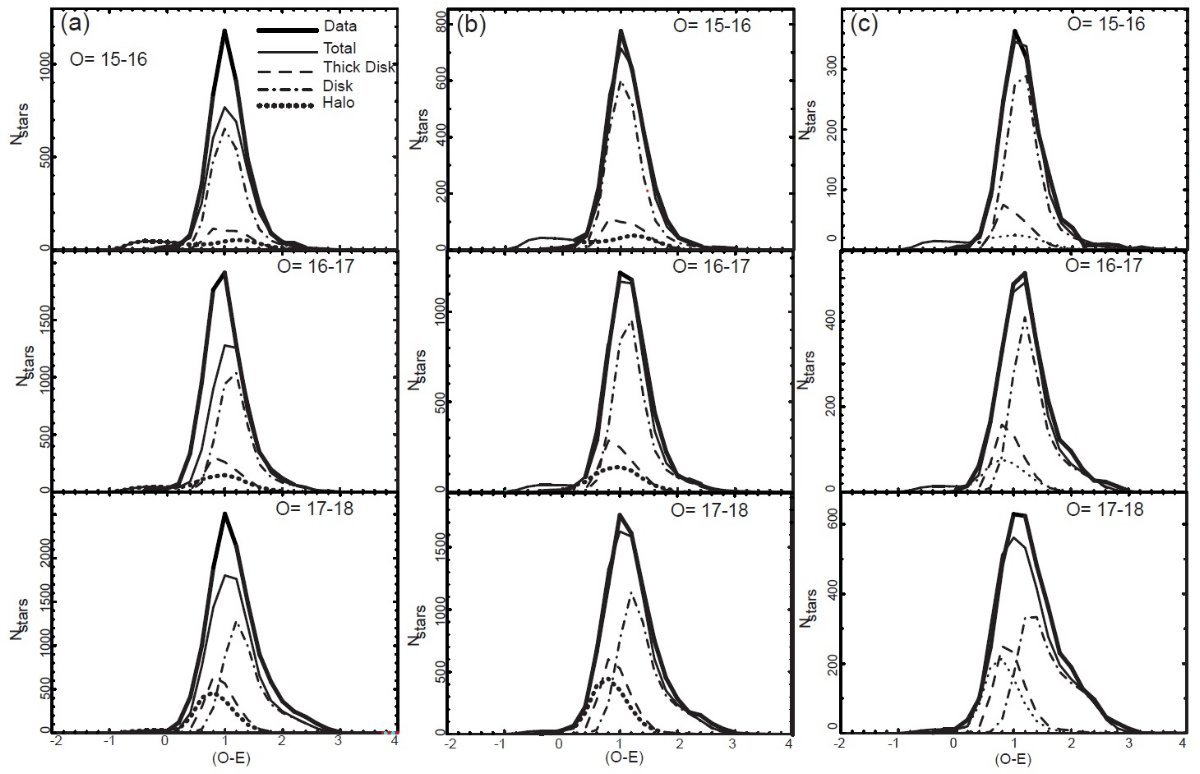
減光補正 減光補正には Schlegel et al. 1998 を用いた。その E(B-V) を乾板の E(O-E) に変換して用いた。各乾板位置の 平均 E(B-V) は表1に載せた。殆どの領域で赤化の影響が小さいことが判る。 図3には赤化補正による見かけ等級とカラーの変化を減光が比較的大きな P568 領域について示した。 非対称性を生む星は何か? 非対称性を生む星は何かを確認するため、銀河系の構成要素、薄い円盤、 厚い円盤、ハローを区別しなくてはいけない。このため、3次元銀河系モデル GALMOD (Larsen, Humphreys 2003) による各成分の星計数への寄与を計算した。 図4には観測カラー分布をモデルと比較している。 カラー分布だけから特定の銀河系成分を分離することは不可能だが、ある成分 がどのカラー範囲に最も寄与しているかは分かる。 カラーによるグループ分け カラーのゼロ点は乾板ごとに揺らぐので、カラーの絶対値でグループ分けをすると 星計数が狂う可能性がある。そこで、カラー分布のピークを基準点にとり、それに 基づいて相対的なカラー分類を行った。このピークは円盤 G-型主系列星に相当し、 準矮星のターンオフにあたる。図5にはカラー分布を放物線でフィットして求めた ピーク位置を示している。このピーク位置 T = (O-E)peak を基準にした分類は以下の通り。 青: (O-E) = [T-1, T] mag 中間:(O-E) = [T-0.5, T+0.5] mag. 赤: (O-E) = [T+0.5, T+1.5] |
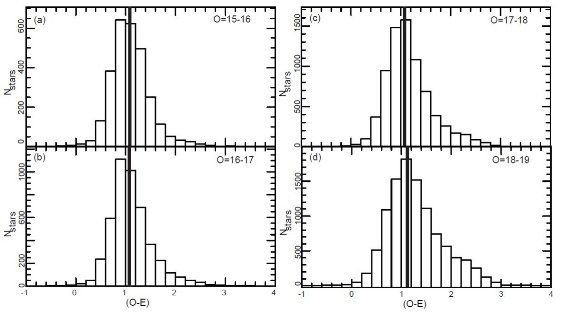 図5.P505 (24, +47) のカラー分布。O-等級で分別した。(a) 15 - 16. (b) 16 - 17. (c) 17 - 18. (d) 18 - 19. (O-E) のピークは黒縦線で示す。 O-等級が 17 mag より暗いところでは青領域の星は厚い円盤とハローの星が多い。 中間カラーでもハローと厚い円盤からの寄与は大きいが、明るい星では薄い円盤星 が支配的である。それでも 17 等より暗くなると、ハローと厚い円盤星が薄い 円盤とほぼ同じくらいになる。赤い領域では等級に関係なく、薄い円盤星が 圧倒的である。 |
3.1.ブレンドした星像の補正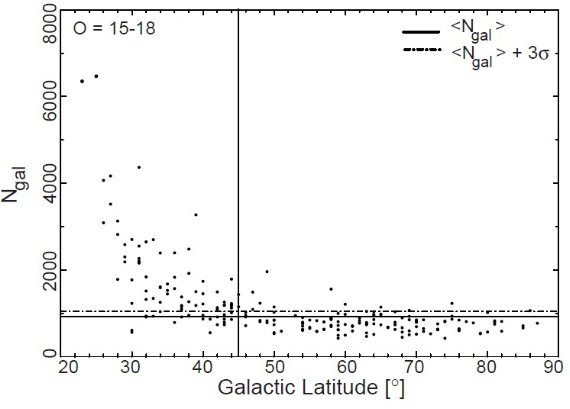 図6.銀河、非恒星の数と銀緯の関係。|b| ≥ 45 の乾板を使って平均を計算した。 3.2.完全性テスト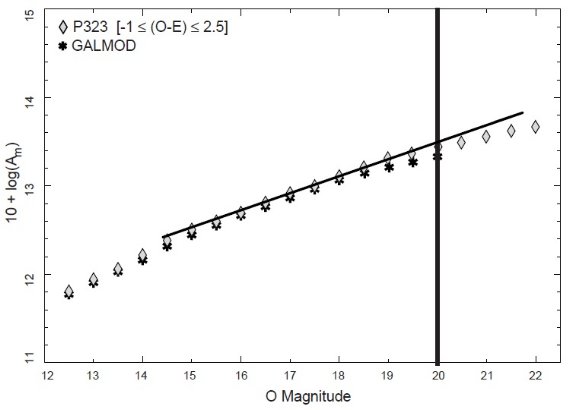 図7.P323 (65, +86) の光度関数。最少二乗フィットで完全性限界を決める。 O = 20 付近で "turns over" するのでそこを限界値とする。アステリスク= GALMOD による予想値。観測と平行することに注目せよ。 3.3.星計数比とその不定性星計数比の定義減光補正を行った後、O = 15 - 完全性限界まで1等区間で星計数を行う。 これは 120 領域内の 560 万星に対して行われた。星計数比は単に、各乾板 における星計数を、対応するペアの領域での星計数で割った値である。 |
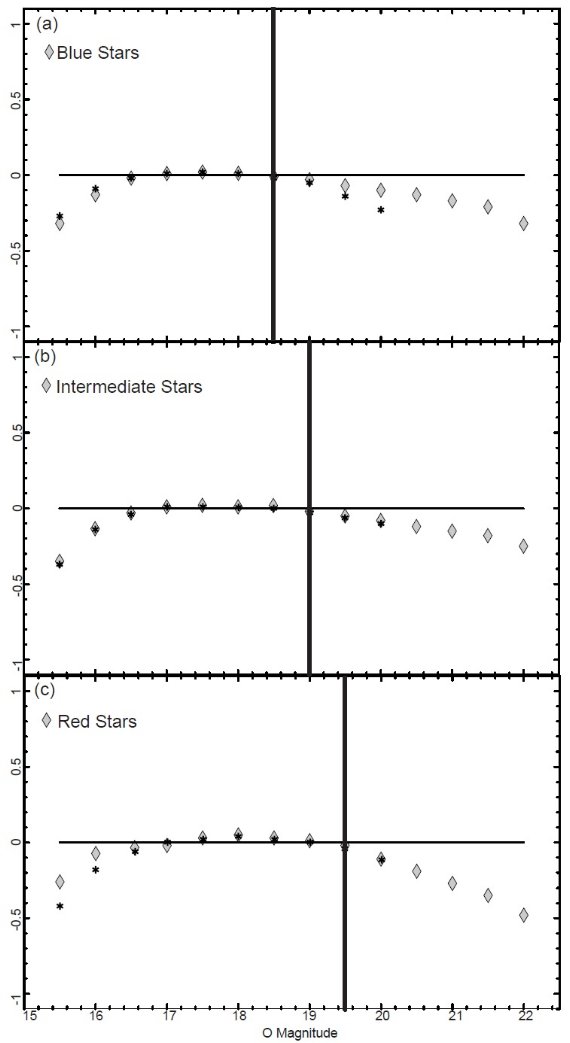 図8.光度関数に対する最少二乗フィットからの残差を用いて完全性限界を 求める。アステリスク=GALMOD 予測に対するフィットからの残差。 星計数比=1 銀河系が対称ならこの比は1である。もちろんペアが完全におなじ対称位置 ではないので実際には1の周りに揺らぐであろう。 |
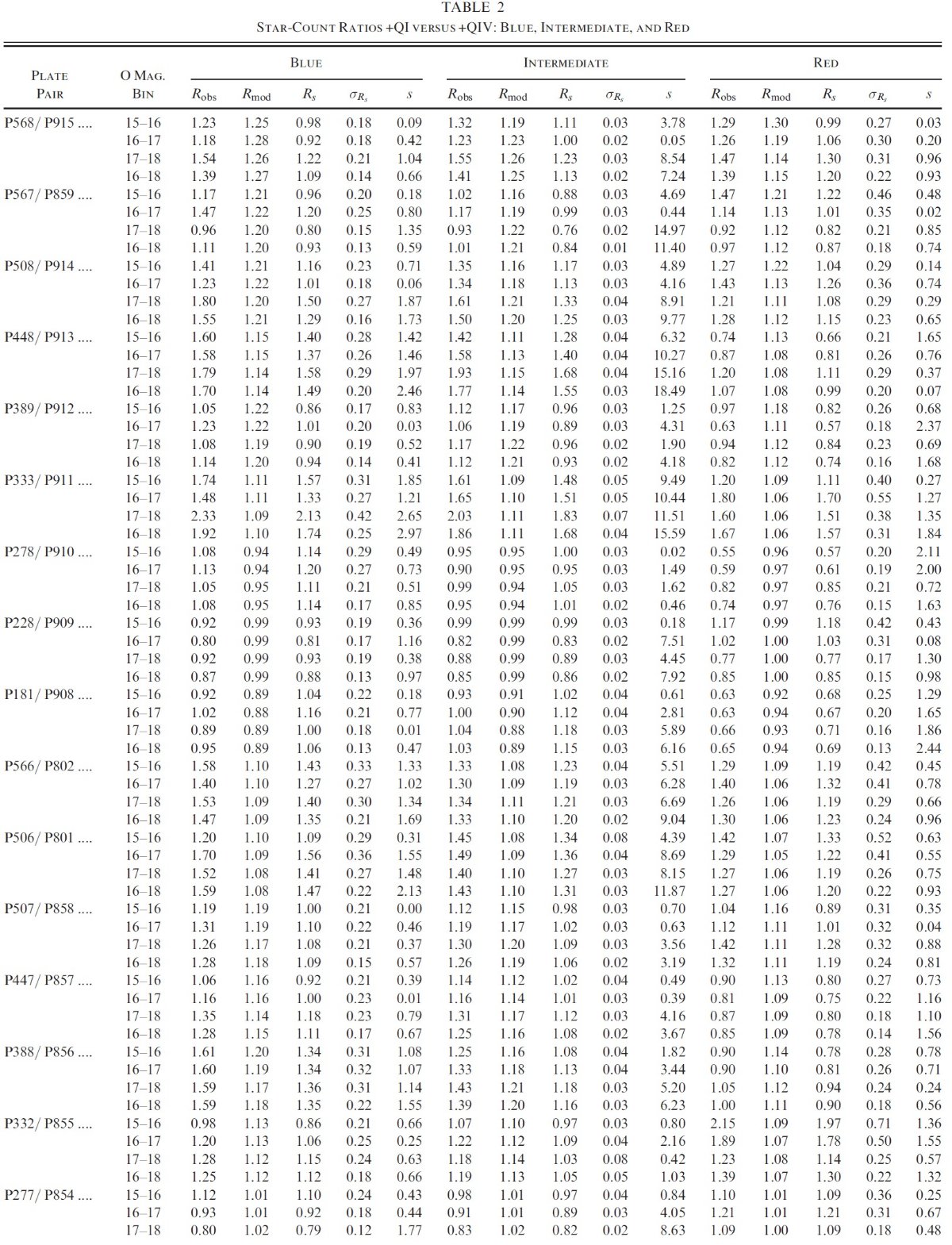
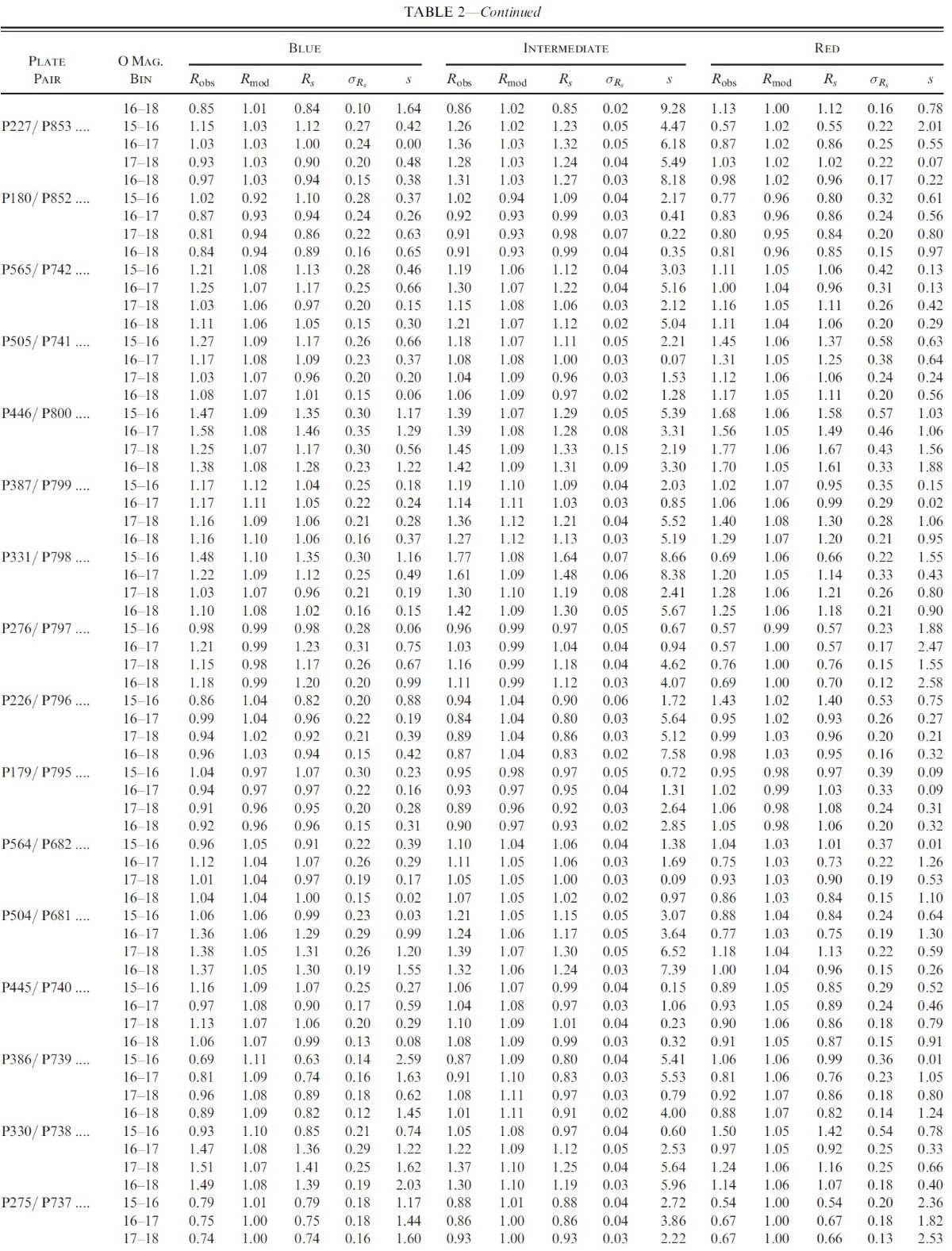
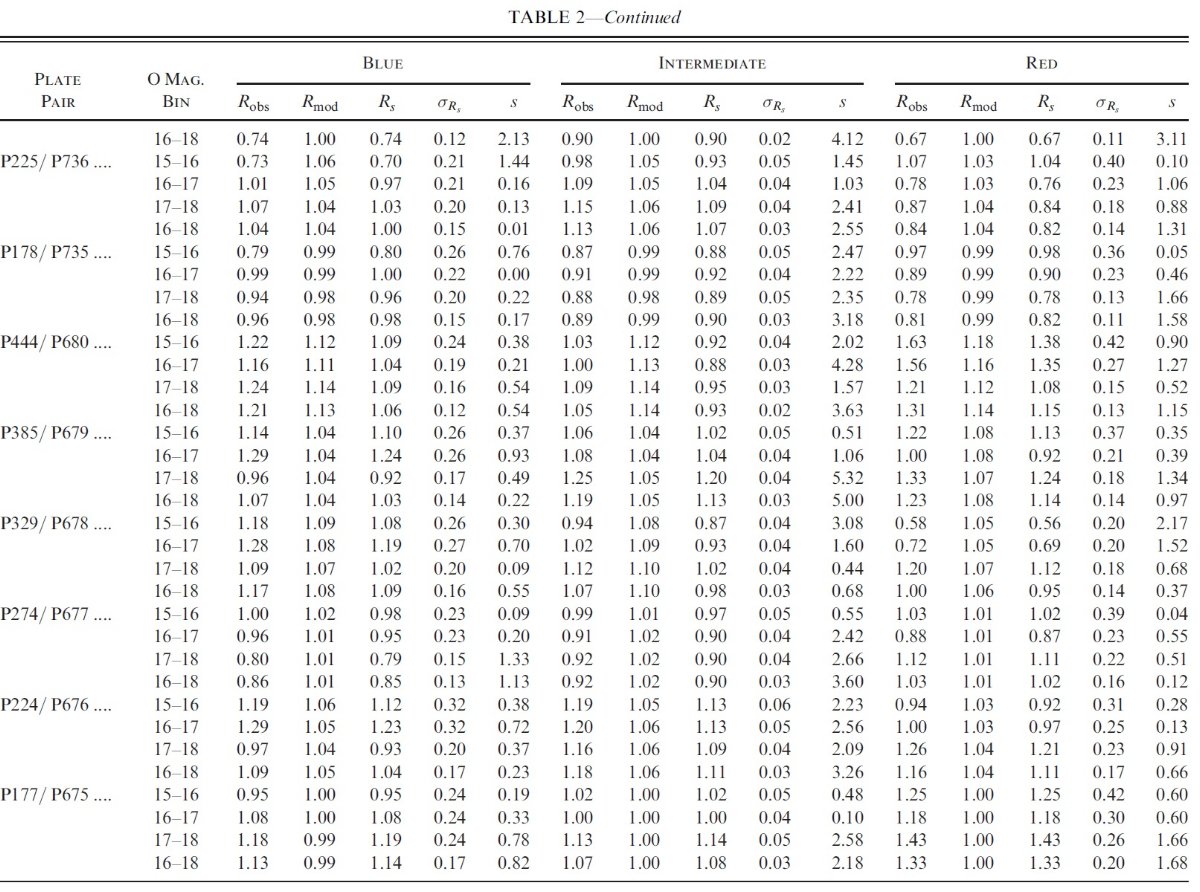
4.1.第1象限対第4象限。銀河面上側s パラメタ―16 等より暗い青グループ星は、ハロー/厚い円盤 星が彼らとしては最大の 貢献度を示している。多くの領域で、 15 - 16 等帯ではハロー/厚い円盤 星 はほんの僅かしか寄与していない。そこで、図9では 16 - 18 等の青い星 に対する s の分布を示す。 s パラメタ― = (Rs-1)/σs ここに、Rs = Robs/Rmod であり、 Robs = 北銀河の星計数/対応南銀河位置の星計数、Rs = そのモデル版。&sigmas = Rs の不確定性。 s パラメタ−は Rs が 1 からどのくらい離れているかの指標である。 Rs と s はある領域の星数が超過しているか不足しているかを、 統計的に評価する有用な量である。 第1象限の超過が非対称の原因 表3をざっと見るだけでも、第1象限の星数が対応する第4象限のそれに 比べて多いことが判る。GALMOD の予測と比べると、係数の非対称が現れるのは、 第1象限で星が超過しているためであり、第4象限で不足しているせいではない ことが判る。 |
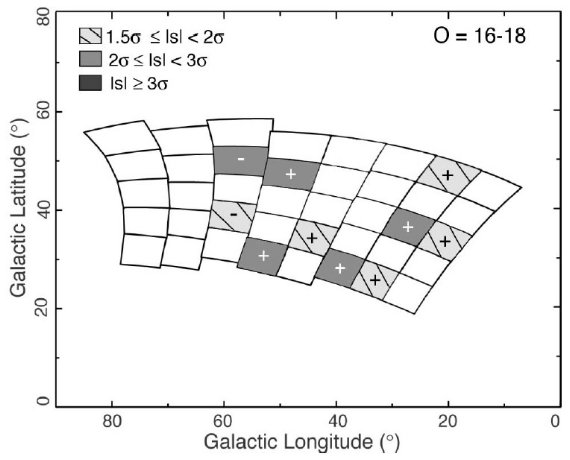 図9. O = [16, 18] 等の青クループ星のパラメタ― s 分布 |
4.1.第1対第4象限:銀河面上方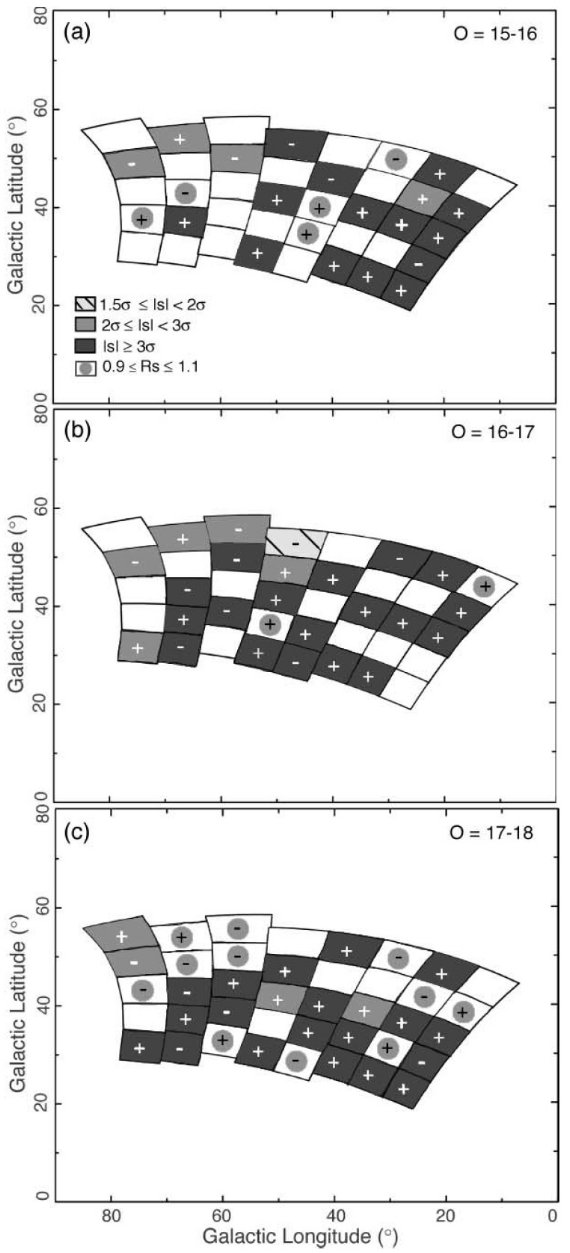 図10.等級帯別の中間色グループの s 分布。(a) 15 - 16 mag. (b) 16 - 17 mag. (c) 17 - 18 mag. |
青い星の超過分布 図9では s の値によって、超過(+) または不足 (-) の程度を4区分に分けて 図示した。多くの領域で超過しているが、一様ではない。暗い等級帯に行くほど 超過領域の数も、超過の程度も大きくなることが判った。これはハロー/厚い円盤 の星の影響が強まるためと考えられる。結論として、青い星の超過にはむらがある と考えられる。それでも、b = 30 - 40, l = 20 - 50 のあたりではかなりな超過 が存在する。 中間色星の超過分布 中間色グループはカラー分布のピークを含み数は最大である。そのカラー区分は 青い星と重なっている。図10に s の分布を示す。暗い星ほど s が大きい。s が 大きくなる理由の一つはサンプル数が大きいので、σ が小さくなるためもある。 図10は第1象限において超過が生じる領域を明瞭に示す。非対称領域は l = [20, 60], b = [25, 45] である。特に b = [30,40] 帯は l = [20, 60] で つながった帯を形作っている。 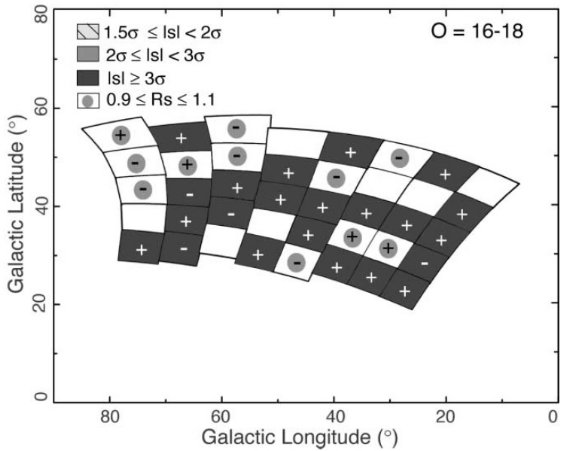 図11. O = 16 -18 に合体した中間色グループの s 分布。 |
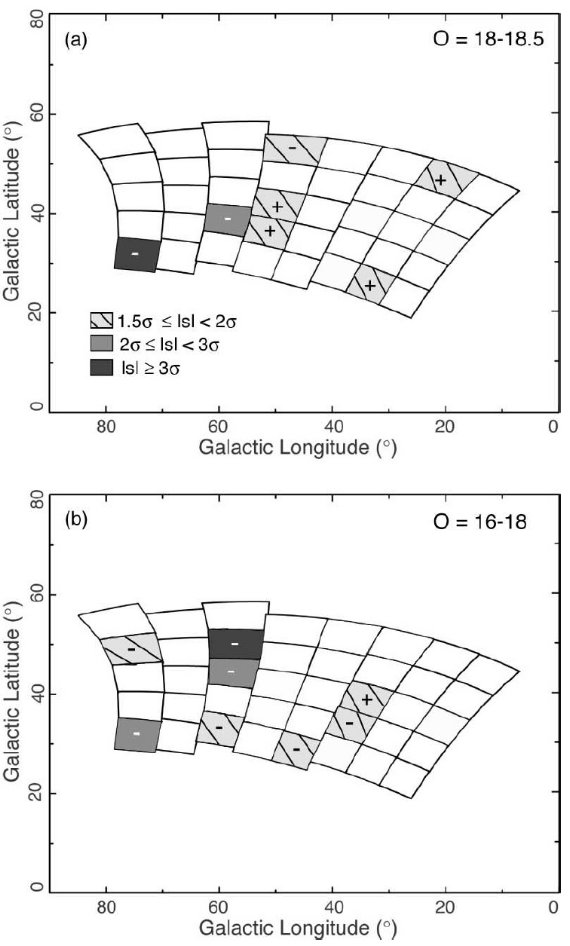 図12.赤い星グループのパラメタ― s 分布。上:O = [16, 18], 下:[18, 18.5] | 赤い星グループ 赤い星グループの大部分は薄い円盤星である。暗い方では K-, M-矮星の 比率が高まる。混入の影響が大きい領域を除去したため、赤い星のサンプルは 少なくなった。図12の赤い星の s 分布からははっきりした非対称性の存在は 認められない。この結果は円盤星は非対称性には殆ど寄与していないことを 示す。 ハロー星 ハロー星の寄与をもっとはっきりさせるため、青いカラーを二つに分け、 (O-E) = [-1.0, -0.5] を極青グループとした。O = 16 より暗い方では 極青星の大部分はハロー星と考えられる。このカラーサンプルは数が少なく、 従ってエラーが大きくなり、 s の減少につながる。図13は極青グループ O = [16, 18] の s マップである。しかし、このマップには、青、中間マップ で超過が見られた領域に何の超過も見えない。 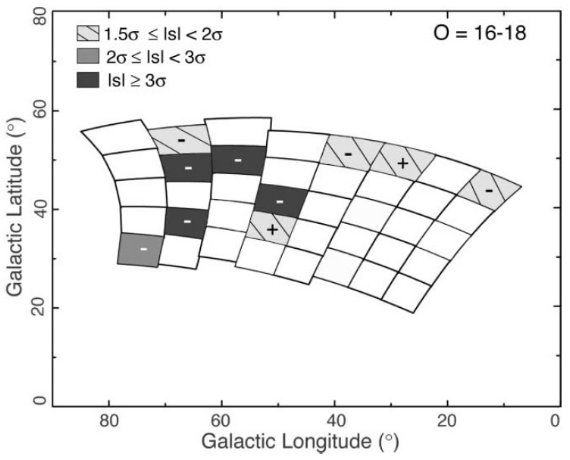 図13.極青グループの s 分布。 |
|
非対称性領域を描いた 図14に第1象限銀河面上側の非対称性領域を示す。境界は星超過の大きい 領域を含む比較的規則的な形を選んだ。表3にはそれら 15 領域の平均 Rsf とエラーを載せた。参照用の正常なスカイとして隣接する 9 領域を選び、コントロール 領域と名付けた。それらの平均値を表4に示す。 寄与する成分 円盤星は超過に寄与していない。ハローと厚い円盤の星が主原因であろう。 しかし、厚い円盤がその犯人である可能性が高い。超過を示す星の平均カラーは 低メタル星のターンオフに対応する。それらが厚い円盤の主系列星であると仮定して、 Mv = +5.6 (Reid 1998) と仮定すると、これらの星は平均 d = 0.9 - 2.3 kpc で 銀河面から 0.5 - 1.5 kpc 上にある。 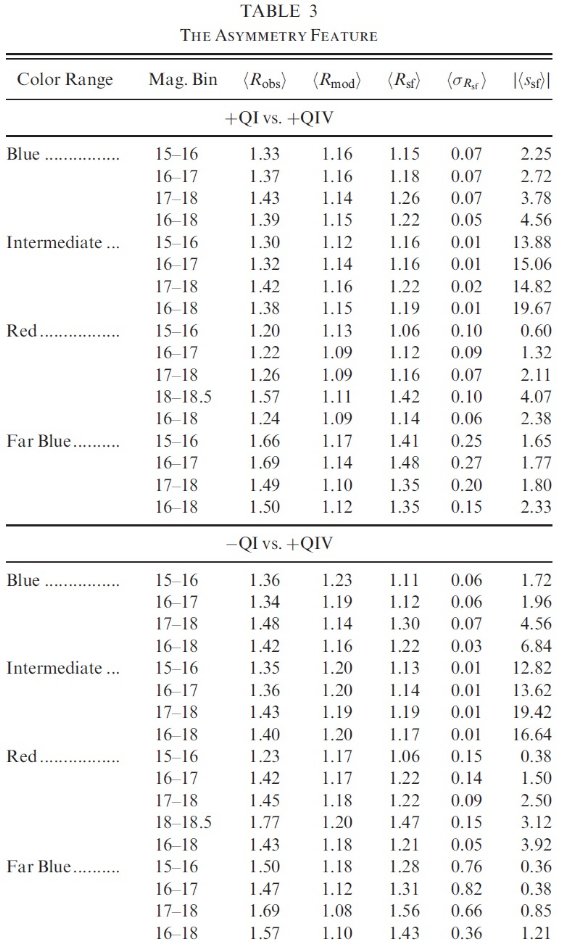 表3.非対称性の特性 |
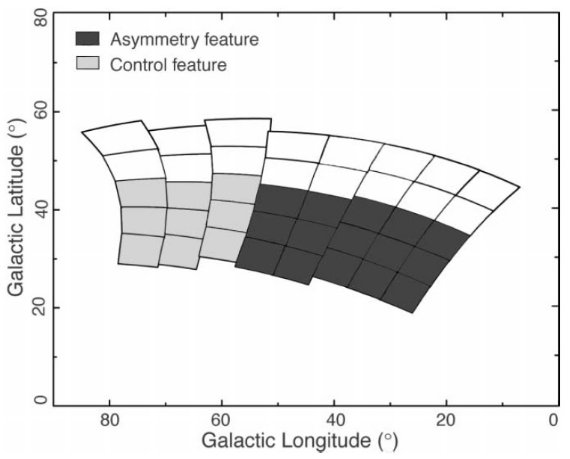 図14.第1象限での対称性。l =[20, 55], b = [20, 45] 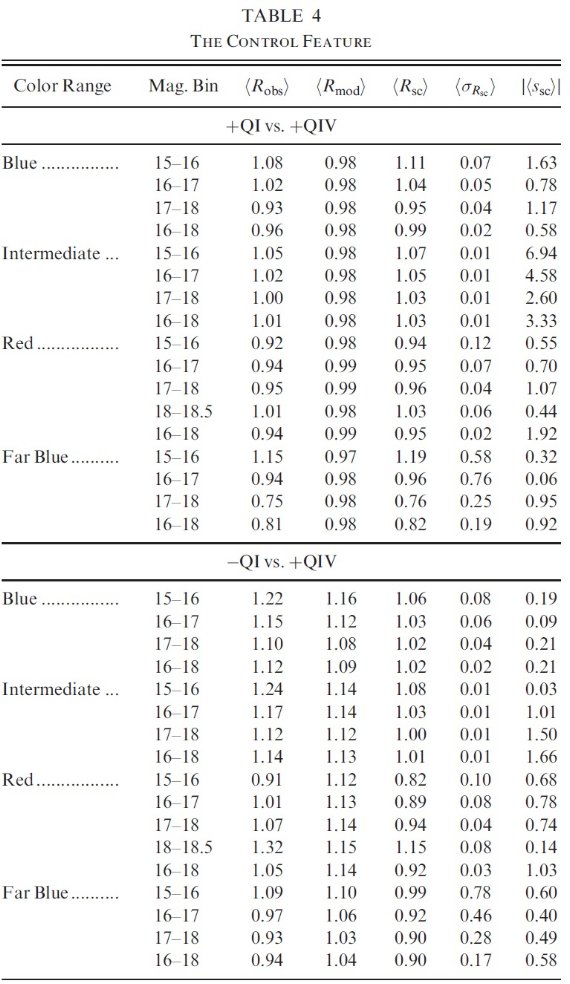 表4.コントロール特性 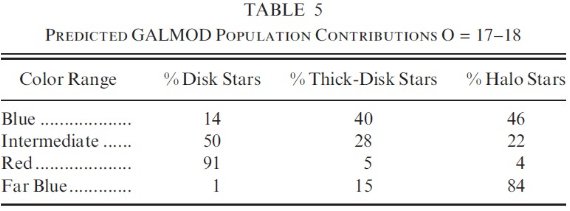 表5.GALMOD による O = [17, 18] の寄与予想。 |
|
1.マージャーの名残り 非対称の場所はサジタリウス矮小銀河の軌道とも、マゼランストリームとも 無関係である。その上、モデル計算ではマージャーのデブリは天球上に大円を 描くが、非対称域は銀河面に平行である。したがって、この仮説はありそうに ない。 3軸不等の厚い円盤 3軸円盤の主軸が第1象限にあると観測されるような超過を引き起こすであろう。 ただその場合、超過はもっと大きな銀経にまで及びそうである。また、3軸ハロー ならもっと高銀緯に影響が及ぶであろう。ただし、もっと暗い等級まで観測が 到達すると新しい特徴が見えてくるかもしれない。 |
バーとの作用 我々の視線方向は中心バーの方向と近いことは注意に値する。しかし、円盤バー が 1 kpc 上方まで伸びているとは考えにくい。しかし、厚い円盤の中にバーが 存在する可能性はまだ研究されていない。 高速回転するバーは重力的な "wake" を引き起こし、後に星を集める。 従ってバーに反応して、速度分布にラグが見出されるであろう。 |