New Models for the Evolution of post-AGB Stars and Central Stars of Planetary Nebulae

　アブストラクト　

　１．イントロダクション　

　２．入力物理　

　２．２．巨視物理　

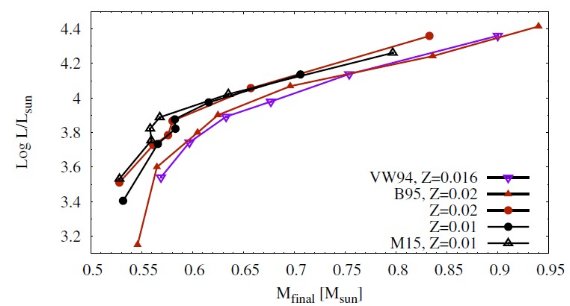
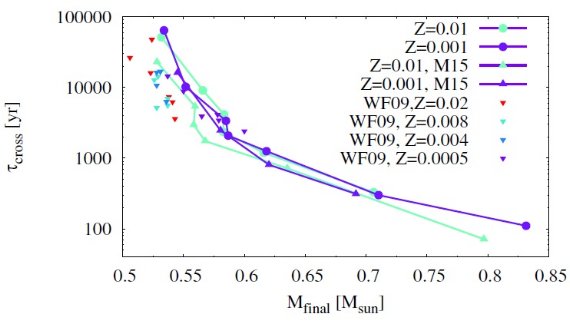
２．２．２．対流ミクシング　 　ミックシングレングスセオリー　 　太陽で較正した結果、α = 1.825 を採用した。 　CBM = 対流境界混合　 　CBM = 対流境界混合の扱いは、速度場が指数関数型に減衰する仮定で Freytag et al 1996 の拡散係数 Dov を採用した。 　　Dov = Do exp(-2z/fHP) ここに、Do = vαHP は対流境界付近での拡散係数、 HP = 圧力スケール高、z = 形式的な対流境界からの高さ、 f = フリーパラメター。 対流境界混合(CBM)領域の広がりは Dov が Dcut-off = 10-10Do になるまでとした。この値は ゆっくりした進化段階では重要である。この領域内では混合は完全とする。 　対流境界の場所　 　我々のモデルでは対流境界の場所は、(i) コア水素燃焼の対流核境界 fCHB, (ii) コアヘリウム燃焼の対流核境界 fCHeB, (iii) 外層対流層の下側 fCE, (iv) 熱パルス駆動対流層境界 fPDCZ である。 　H 燃焼核対流層の f はいくつ？　 　一般には上部主系列星のモデル計算の際、対流核を 0.2 HP 広げると観測に合うことが知られている。我々の Dcut-off に関しては、Mi > M2 では fCHB = 0.0174 とし、それより下では Mi に対し線形に落ちて Mi = M1 でゼロとする。表１を 見よ。 合う結果が得られる

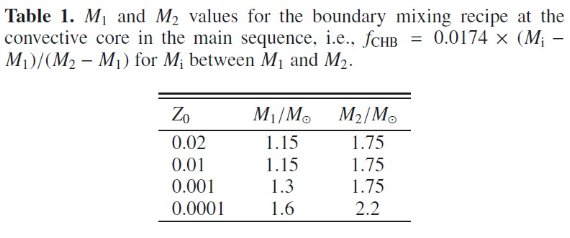
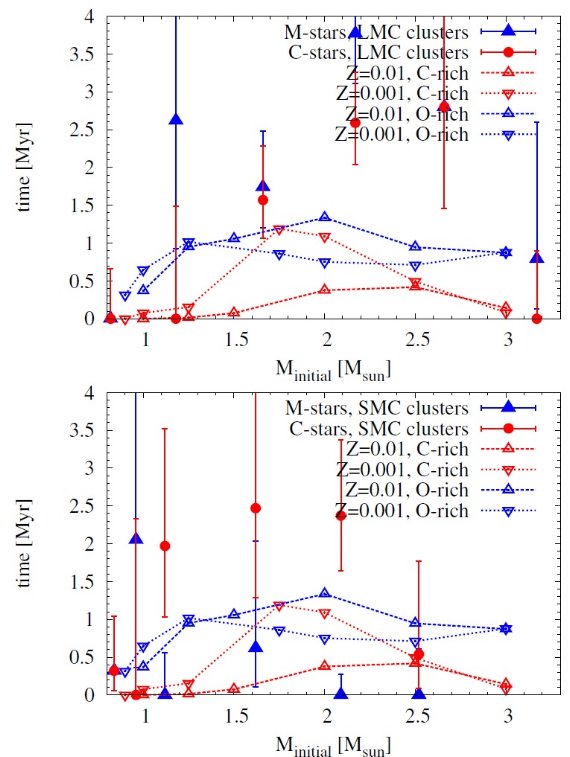
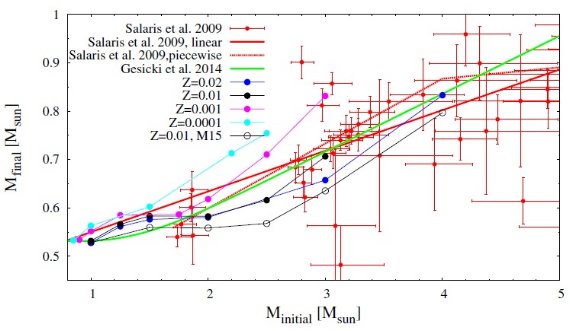
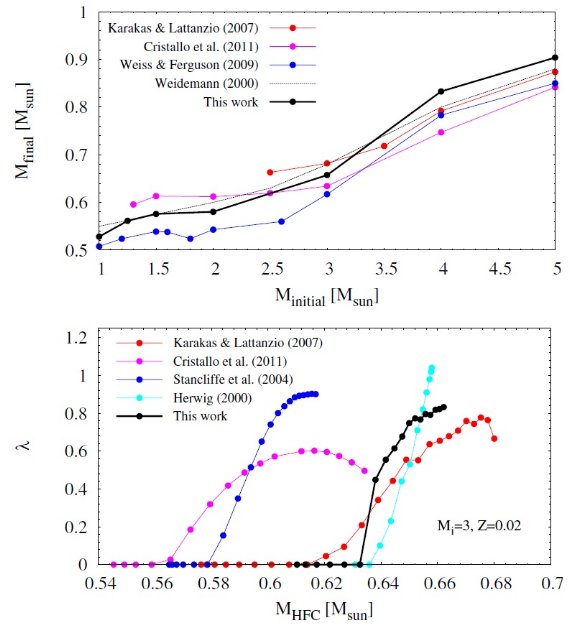
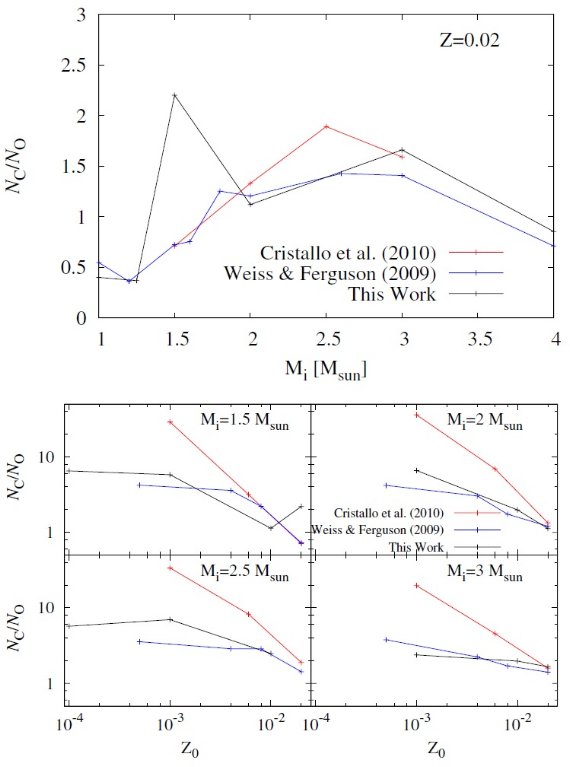
表1．主系列の対流核における対流境界の取り扱いに使用する M1 と M2 の値。 fCHB = 0.0174 (Mi-M1)/(M2-M1). 　He 燃焼核対流層の f はいくつ？　 　He 燃焼核対流層の f はさらに不確実になる。他の値を選ぶ強い理由がない ので、全ての星に対し fCHB = 0.0174 とする。 　fCE と fPDCZ　 　特に重要なのは、熱パルスにおける CBM である。CBM なしの低質量 AGB 星 モデルではサードドレッジアップ (3DUP) が起きないかとても非効率である。 しかし、これは低質量 AGB において炭素星比率 Nc/No > 1 であるという 観測と矛盾する。また熱パルス駆動対流層の底では、 CBM は post-AGB 星 PG 1159 星の O-存在量を説明するために必要である。 （Herwig et al.1999) fCE と fPDCZ の値は、 s-元素の量と 初期最終質量関係（白色矮星）を観測と合わせるために調整される。 我々は fCE = 0 と fPDCZ = 0.0075 を採用する。

　３．ZAMS から AGB までの進化　

AGB　進化モデル　 　表２に Zo = 0.02, 0.01, 0.001, 0.0001, Mi = [0.8, 4] Mo の範囲から 27 系列の MS 開始から TP-AGB 終了までの結果を示す。Mf = [0.5, 0.85] Mo であった。Weiss, Fewrguson 2009 に従い、 　　　Y = 0.245 + 2 Zo とした。主系列、赤色巨星、 He 核燃焼期の寿命はそれぞれ τMS, τRGB, τHeCB とする。通常寿命は Mi が小さ いほど、Zo が大きいほど長くなる。表２の第４列には He 核に火が付くのが He 核フラッシュ (HeCF) ＝ "yes" か違う "no" かを示す。第５列を見ると、Zo = 0.02, 0.01 では Mi = 2 Mo 付近で τHeCB が最長になることが 分かる。低メタルではもう少し低質量にピークが移る。それより低質量星では τHeCB ∼ 0.1 Gyr の一定値となる。 ヘリウムフラッシュを起こす縮退核質量は一定であることがその原因である。 一方高質量側では縮退から非縮退へ移る際にヘリウム核質量が減少し、その後 は増大していく。Mi と共に He コアが小さくなるので、τHeCB は短くなっていく。He 核燃焼の終了から熱パルス開始までの早期 AGB 期間 τeAGB の期間は He 核燃焼後に残された He 質量の大きさにも 影響される。同じ理由で、第１熱パルス開始時の水素欠乏核質量は Mi と共に はっきりした極小を示す。表２の第７列を見よ。これが非常に効率的な第３ ドレッジアップが Mi < 2.5 Mo で強調された初期最終質量関係の強調され たプラトーを示す理由である。 　炭素星の形成　 　過去２０年間 TP-AGB は多くの研究の対象であった。ここでは詳細を省くが、 post-AGB 星は水素欠乏核の性質と外層の CNO 量に影響される。 非常に効率的な第３ドレッジアップの結果、一定質量以上の星は TP-AGB 期に C-リッチになる。その下限質量は Mi = 1.5 Mo(Zo=0.02), 1.25 Mo(Zo=0.01), 1 Mo(Zo=0.001), 0.85 Mo(Zo=0.0001) である。図１は我々のモデルが作る炭素 星が LMC, SMC の球状星団の観測から推定される炭素星の質量範囲にあること を示す。Mi ≤ 1.25 Mo では第３ドレッジアップがないために炭素星が形成 されず、 Mi > 3 Mo でもできない。 　炭素星のマスロスは急増　 　AGB 星が炭素星になると C-リッチ分子のオパシティのために表面温度が低下 する。半径が大きくなる結果、炭素星のマスロスは急増し、炭素星形成後は数 回の熱パルスの間で水素外層が失われ、AGB を離れる。

図１．Zo = 0.01 と 0.001 の C-リッチ、O-リッチ　AGB 星の寿命。LMC(上)と SMC(下)の観測結果を Girardi,Marigo 2007 のモデルと比較。我々の計算では Mbol < -3.6 を O-リッチとすると Girardi,Marigo 2007 の結果と合う。これ が表２の τTP-AGB が図１と合わない理由である。

図２．銀河系円盤 AGB, post-AGB 星の炭素、酸素存在量。上線は Zo = 0.02. 下線は Zo = 0.01。 青線＝強い第３ ドレッジアップを経験した星の経路。黒線＝第３ドレッジアップをあまり経験 しない星の経路。赤線＝ 4 Mo(Zo=0.02) 星で第３ドレッジアップとホット ボトム燃焼を経験した星の経路。log εX = log (NX/NH) + 12. 　モデル炭素星を観測と比較すると　 　炭素星が数回の熱パルスしか経過しないことは図２に見られる PNe の C/O データとも合致する。もし、炭素星が多数回の熱パルスを経過するなら PNe の C/O 比はもっと高い値にまで分布するだろう。つまり、C 量に関しては我々の モデルが TP-AGB から離れるのはちょうど正しい時期であったということである。 さらに我々のモデルは図２に示すように、 M-, C-型星の C/O 比（ Lambert et al.(1986), Smith, Lambert (1990) ）および、post-AGB 星の C/O 比をも正しく反映する。 　初期最終質量関係 (IFMR)によるチェック　 　第３ドレッジアップは、初期最終質量関係 (IFMR) とコアマス光度関係を 決める。どちらも post-AGB 進化のタイムスケールを決める。図３に示す我々 の IFMR は観測から得られたものとよく合う。これは、我々の post-AGB は 適切な初期質量の星から進化したものであることを意味する。Weiss, Ferguson 2009 や Miller 2015 のように、外層対流層底部での対流境界混合を強くした モデルは Mi = 3 Mo 付近で小さすぎる Mf を与えるので適切でない。 　モデルはインターシェル層の組成と合う　 　我々のモデルは図4に示すように、PG1159 星 （ Werner, Herwig (2006) ）の観測から求まったインターシェル層の組成とよく合っている。これは重要 な結果である。なぜなら、 PG1159 星から決まる AGB インターシェル組成は fPDCZ に制限を与えるほぼ唯一の手段だからである。fPDCZ はヘリウムフラッシュの強さとそれに続く 3DUP に影響する。図4を見ると、 fPDCZ = 0.0075 は PG1159 星の O 量を再現することが分かる。

図３．このモデルとMiller15 モデルの初期最終質量関係を星団観測から定めた Salaris et al 2009 と Gesicki et al 2014 の半経験的関係と比較。 図４．post-AGB 星の He, C, O インターシェル組成。モデルと PG1159 タイプ 星観測結果との比較。高 log g 星の大部分は重力安定構造への経過中で高い He 量は元々のインターシェル組成を表さないかも知れない。

図５．上：Zo = 0.02 モデルの初期最終質量関係の比較。 下：λ = 3 Mo Zo 0.02 モデルでの第３ドレッジアップ効率係数の比較。 　他のモデルとの比較　 　図 1 - 4 の結果は、TAGB 期の水素欠乏核の成長と炭素汚染に関する AGB と post-AGB 星の観測から我々の post-AGB 星モデルは正しい出発点にある と言えることを確証している。図5の上図は我々の初期最終質量関係を他の最新 モデルと比較したものである。これを見ると、我々の結果が他の計算と合って いることがわかる。図5下図は Mi = 3 Mo, Z=0.02 ケースに対し、3DUP 効率 λ を Mcore の関数として示したものである。この場合も我々のモデル は他のモデルの散らばりの範囲内に収まる。この散らばりは主に、境界混合過程 の扱いの差に起因し、モデルの不確定要因となっている。

図６．TP-AGB 終了時の C/O 比の予想値の比較。 　 C/O 比の予想も他モデルと合う　 　図６では我々の post-AGB モデルでの C/O 比を、他のモデルでの AGB 進化 最終端での C/O 比と比べた。図６上で分かるように、我々の C/O 比は Weiss, Ferguson 2009 と Cristallo et al. 2011 のソーラーと近い。例外は Mi = 1.5 Mo (Zo=0.02) モデルで我々はこれに高い C/O 比を与えている。これは、 TP-AGB の最終末期に熱パルスが起き、小さい外層質量でドレッジアップされた　 C を希釈したので C/H が上がったのである。

　４．Post-AGB 進化　

４．１．結果の記述　 　post-AGB 進化の概略　 　AGB からの離脱は定常星風が水素外層の質量を下げるからである(Schonberner 1979). 結果として、この遷移は穏やかに進行し、このため post-AGB の開始 ＝ AGB の終わり、を明確に定義するのは難しい。図７に、有効温度と外層質量 の関係を Zo = 0.001 の場合に対して示す。外層質量がコア質量と同じくらいに なると(Menv/Mstar = 0.5 - 0.1) モデルは外層質量の減少と共に青方向に動き 出す。最初は外層質量が大きく減少しても有効温度の変化は小さい。この状態は 外層質量が白色矮星外層質量の数倍になるまで続く。この点を過ぎると、外層 質量の小さな変化は有効温度の大きな変化に跳ね返る。 大部分のモデル計算では初期の進化のゆっくりした期間に AGB 領域から離れる。 その結果、 AGB の終わりに対する自然な定義は存在しない。 我々は post-AGB の開始を Menv/Mstar = 0.01 と決めた。この時点でモデルは 既にかなり青くなっている。この定義は AGB 終末を一様な基準で決めており、 AGB からの離脱に関する物理的なメカニズムとも合致する。 (AGB から post-AGB への遷移時期に 脈動がどうなっているか一切考慮していないようだ。L と M だけでマスロスを 決めて、それで外層質量を変えて進化させているらしいが、そこでマスロスが 起きるかどうか、脈動周期はどうなるのか、等の検討をモデルで詳しくしてい るのかどうか不明。観測的に押さえるべきか？ ) 　二つのタイムスケール　 　図８には、色々な質量とメタル量に対して、HR 図上の進化を示した。 post-AGB と CSPNe 期進化計算では、通常二つのタイムスケール τtr と τcross を定義する。 τtr は初期 post-AGB 進化の期間で、AGB 的星風が吹き、Teff は Menv にあまり依存しない。一方、τcross は後半 post-AGB 進化タイムスケールで、初期 post-AGB 進化の末期から有効温度最高点まで、 強い Teff - Menv 関係が成立する。我々の計算では log Teff = 3.85 付近で 速い post-AGB 進化が始まる。その上その温度あたりからは、星風は進化速度 決定に二義的な役割しか果たさない。このため、この第２進化期のタイムスケ ールは第１期より信頼できる。post-AGB タイムスケールを τtr と τcross に分けると、 τcross が有用で信頼度の高い物理量となる。 τcross は第1期の post-AGB 星風の知識が不安定なことや、 AGB 期の終末が不明確であることに影響されない。 　　τtr は Menv = 0.01 Mstar から log Teff = 3.85 まで。 　　τcross は log Teff = 3.85 から有効温度最高点まで。 と定義する。 　第2期の開始は？　 　 Vassilidis, Wood (1994), Weiss, Ferguson 2009 は log Teff = 4.0 を境界とした。一方、 Blocker (1995) は、脈動周期 P = 50 d を遷移期の終端とした。 (脈動を計算しているんだ！ ) そこが彼の post-AGB 進化出発点 である。この定義は HE 図上では log Teff = 3.78 - 3.90 に対応する。 それらのどの定義を採用しても τcross は大体同じである。

図７．上：水素燃焼星として AGB を離れた Zo 0.001 星の HR 図。 下：同じ星の log Teff と 水素外層質量 Menv の関係。赤丸: Menv/Mstar= 0.01 の位置で, この論文では post-AGB 期の入り口とした。 　タイムスケールが星質量に強く影響される　 　図８と表３には、水素燃焼 post-AGB 星の進化と性質をまとめた。 強調したいのは、post-AGB タイムスケールが星質量に極めて強く影響される ことである。高質量 ≥ 0.7 Mo では HR 図を横切るのに数百年しかかから ず、光度が二けた下がるのに数千年しか要しない。一方 0.55 Mo では、 横切るのに一万年、光度が一桁下がるのに十万年かかる。この時間はメタル量 にあまり依らない。

図９．HR 図横断タイムスケール。先行研究との比較のため log Teff = 4.0 から最高有効温度までの期間を取った。 VW94 = Vassilidis, Wood (1994), B95 = Blocker (1995), S83 = Schonberner 1983, WF09 = Weiss, Ferguson 2009. 大きな丸＝今回の 計算と WF09 の結果が他より著しく小さなタイムスケールを与えている。 また、 Mf = 0.58 Mo での突然の落下はそれ以前の進化モデルの違いに原因を 辿れることが分かった。 　Mf = 0.58 Mo タイムスケールジャンプ　 　Mf = 0.58 Mo にはタイムスケールのジャンプが見られる。これは以前の進化 でヘリウムコアフラッシュを起こしたかどうかがその後の進化に影響した結果 である。それらは似た値の最終質量で終わるが、 AGB に入るときには異なる 大きさの水素欠乏コア質量を持つ。その結果、AGB 期の長さも、コアの温度 分布、組成分布は異なる。それが 3DUP に反映され、遷移の高質量側では 光度が高く、水素外層の質量は小さい。その結果、Mf ≥ 0.58 Mo では タイムスケールが急落するのである。 　τtr　 　表３によると Mf = 0.53 から 0,58 Mo にかけて、τtr は 急速に縮小し、その後は緩やかな低下を示す。τtr は AGB 期 をどう定義するか、星風の強度がどのくらいかに強く影響される。それら を考慮すると、 Mf = 0.53 Mo で τtr = 2000 - 7000 年、 Mf > 0.7 Mo で τtr = 500 - 1000 年程度であろう。 　水素燃焼　 　AGB 離脱時の熱パルス位相を調整する努力はされていない。しかし当然なが ら、post-AGB モデル系列は水素燃焼型となった。非常に低質量、低メタル量 の 0.8 Mo, Zo=0.001, 0.0001 モデルのみはヘリウム燃焼モデルで AGB を離 れた。また、1.5 Mo, Zo0.001 モデルは LTP = 遅れた熱パルスを経ることと なった。1.25, 2 Mo Zo0.02 の２モデルは VLTP = 非常に遅れた熱パルスを 起こしている。 　ヘリウム燃焼 post-AGB 進化　 　図１０には、計算された３つの ヘリウム燃焼 post-AGB 進化経路に対し、 log Teff と log L の時間変化を示す。 Mf 0.4971 Mo(Mi0.8Mo, Z0.001)＝ヘリウム燃焼モデルの τcross = 487 kyr, Mf 0.5183 Mo(Mi0.8Mo, Z0.0001)＝ヘリウム燃焼モデルの τcross = 334 kyr で、水素燃焼系列、例えば Mi=1Mo, Mf=0.53Mo に対する τcross = 20 - 60 kyr に比べ ると一桁長い。ただし、インターパルス期と同様にヘリウム燃焼星でもヘリウ ム光度が水素光度を上回るのは、図１０に示すように、最初の 100 kyr で残 りは水素燃焼である。post-AGB 期の水素再点火は Teff の一時的低下を引き 起こす。

図１０．TP-AGB と post-AGB 期における、上＝ Teff と下＝ L の時間変化。 時間のゼロ点は log Teff = 3.85 に取った。表示のために青線(mi=1.5Mo) は時間を十倍に拡大して示している。Mi 0.8 Mo の二つはヘリウム燃焼 post-AGB, Mi 1.5 Mo は LTP 星である。 　LTP, VLTP　 外層部の水素量が非常に低い場合、Mi=1.5Mo, Z=0.001 の LTP が そうだが、全 post-AGB 期を通じてヘリウム燃焼を維持する。その時の 表面組成は [H/He/V/N/O/Ne] = [0.036/0.504/0.353/5.8 10-4/ 0.075/0.029] である。この低水素量は３DUPによる希釈効果のせいである。 この星の τcross = 12.4 kyr は同じ質量の水素燃焼星で 3.4 - 2.1 kyr なので随分長い。 非常に低マスの post-AGB 星ではまた複数回のフラッシュを経験する。

　４．２．他のモデルとの比較　

図１１．Post-AGB 質量光度関係の比較。新しいモデルは log L で 0.1 - 0.3 明るい。 　post-AGB タイムスケールが短くなった　 　我々の研究の主な結果は、新しいモデルによる post-AGB タイムスケール τcross が以前の Vassilidis, Wood (1994), Blocker (1995), に比べ１０倍も短いことである。 我々の結果は Weiss, Ferguson 2009 とは一致する。我々と彼らは異なる進化 コードを使っているが、入れた物理は最新である点で共通する。新しいモデルは 図１１に見るように、大部分の Mf に対し、log L で 0.1 - 0.3 明るい。 　星風は進化に効かない　 　水素燃焼 post-AGB 進化の速度は水素外層質量の減少速度で決まる。光度最高 でメタル量も多い、 Mi 4 Mo, Zo 0,02 ケースを除いて、post-AGB 星風は二義 的な役割を占めるに過ぎない。post-AGB 期では ΔMenvwinds/ ΔMenvtotal = 0.15 - 0.35 程度である。 　外層が小さく、明るいので速い　 　今回の計算でのコアマス光度関係は図１１に示すようにこれまで採用されて いたものと大きく異なる。この違いはまた TP-AGB 離脱時に水素外層質量を変える ことになる。

図１２．図９と同じ τcross の比較だが、こちらは最初の Miller15 と比べている。これは同じコードを使い、同じ物理が入っているが、 TP-AGB 進化の際の仮定が異なる。これは 3DUP の扱いの違いが post-AGB 進化に影響する例の一つである。Miller15 モデルは Weiss,Ferguson2009 と より一致が良い。これは両者が TP-AGB モデルで非常に効率の良い対流境界 混合を仮定しているからである。 新しいモデルでは、星は前のモデルより明るく、かつより小さな 水素外層を持って TP-AGB を離れる。その結果、進化速度が速まるのである。 その上、3DUP の効率が高いので、水素外層の高炭素化も進み、 IFMR も変わる。 　 f の大きさで調整　 　対流境界混合効率 f の大きさは post-AGB 進化速度に大きな影響を持つ。 実際、Weiss, Ferguson 2009 は我々より大きな fCE = fPDCZ = 0.016 を TP-AGB 計算で採用して、我々よりさらに早い進化速度を得ている。 図１２にそれを示す。ただし、f を上げると、Mi に対する Mf が小さくなり過ぎる。 これが我々があまり大きな f を採用しなかった理由である。

　５．議論　

　６．結論