Evolution of Low- and Intermediate-Mass Stars to the End of the AGB with Mass Loss

　アブストラクト　

　１．イントロダクション　

　２．計算の詳細　

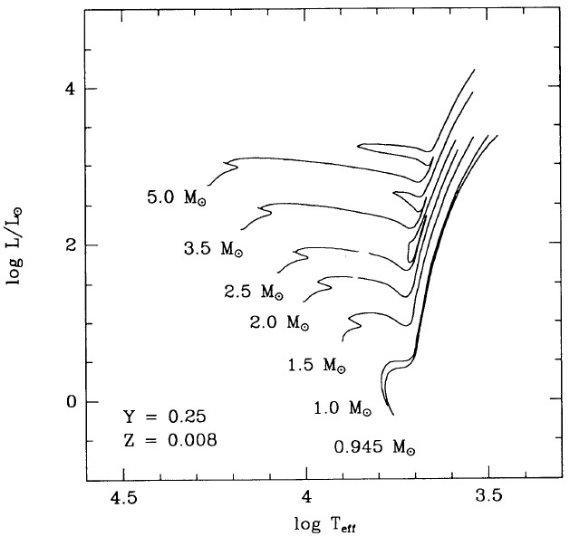
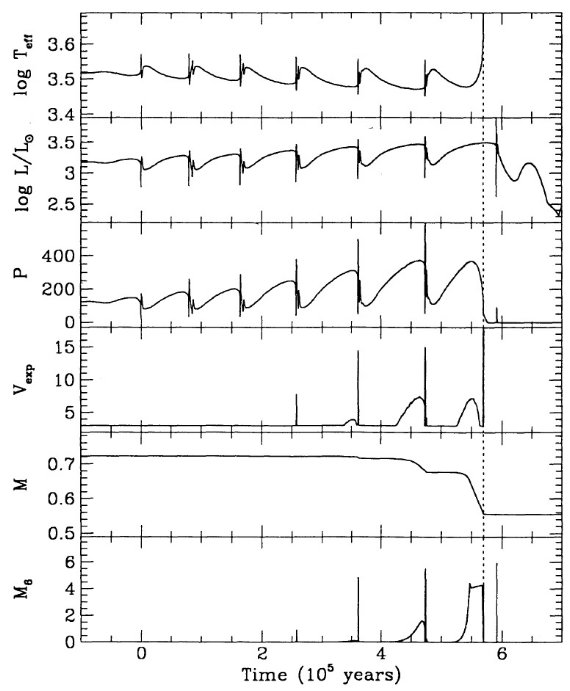
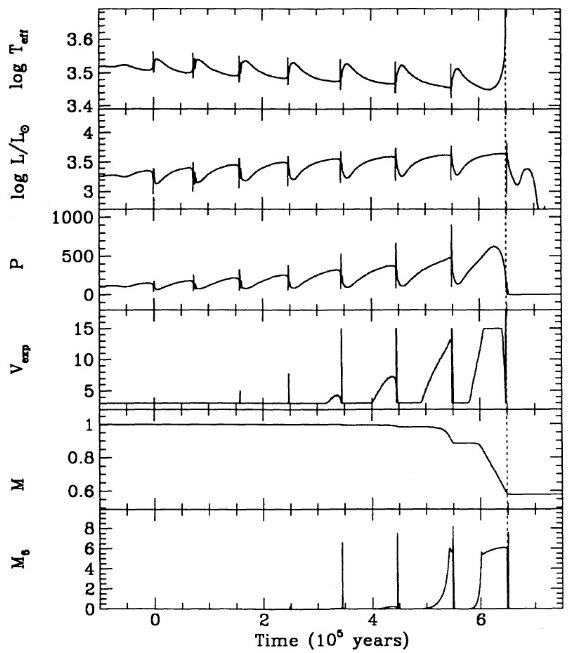
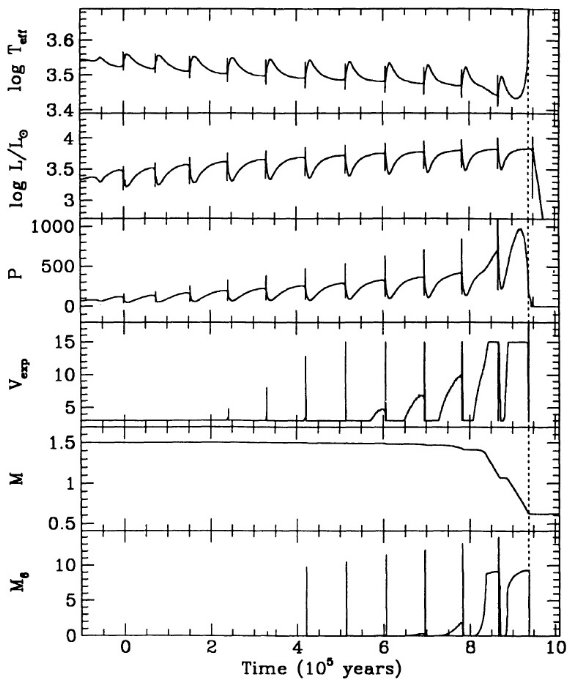
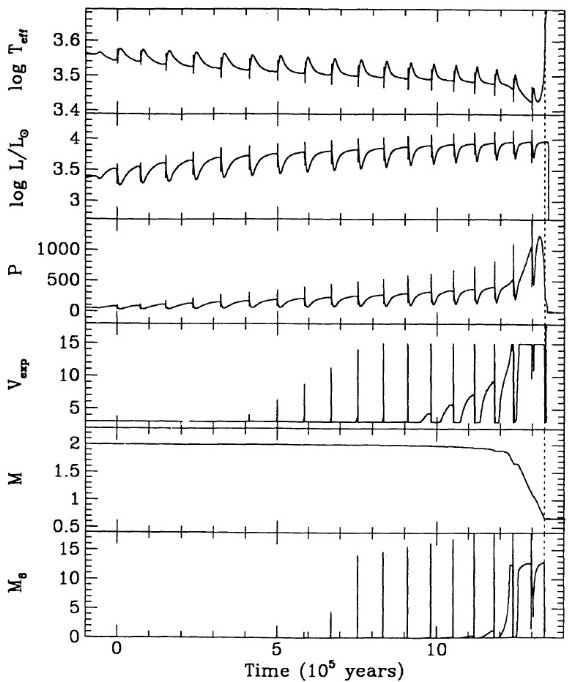
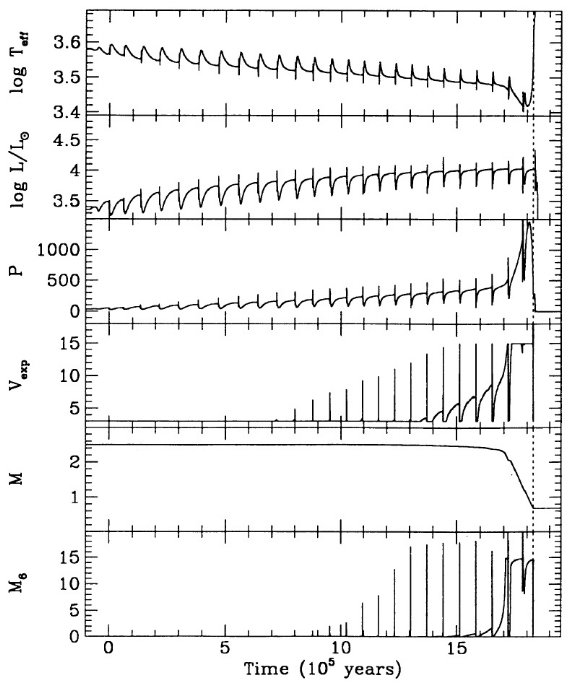
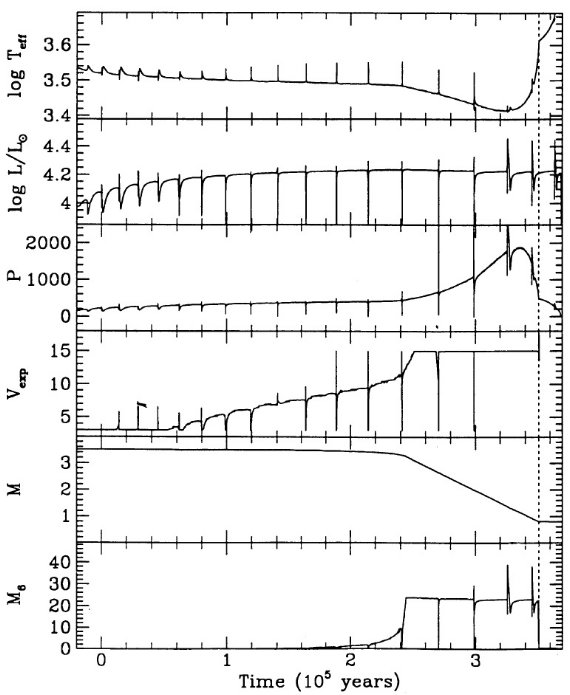
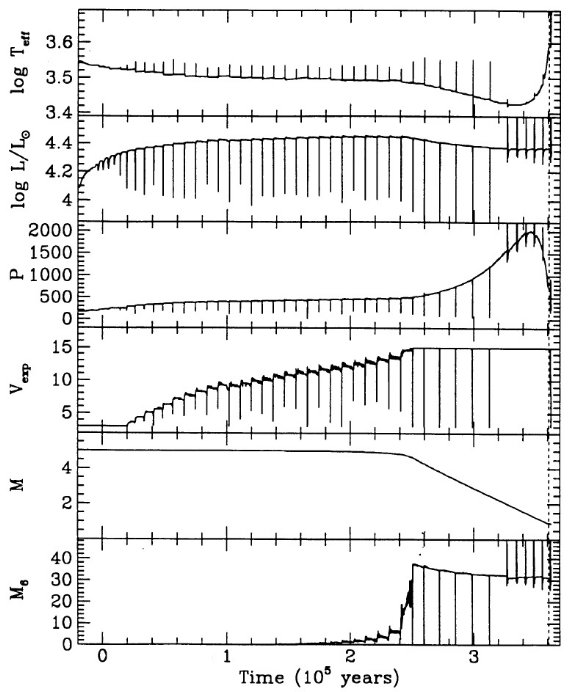
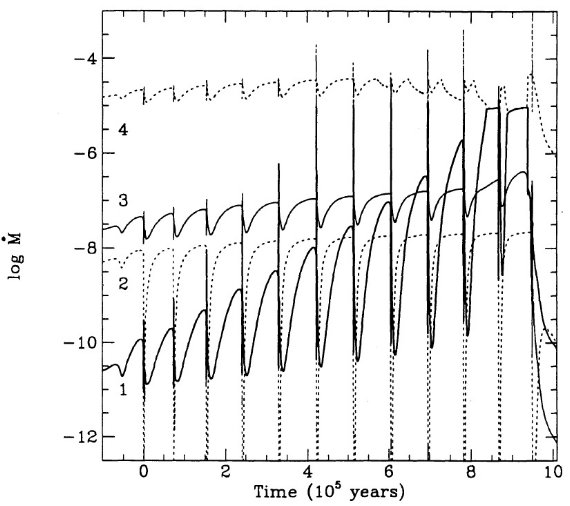
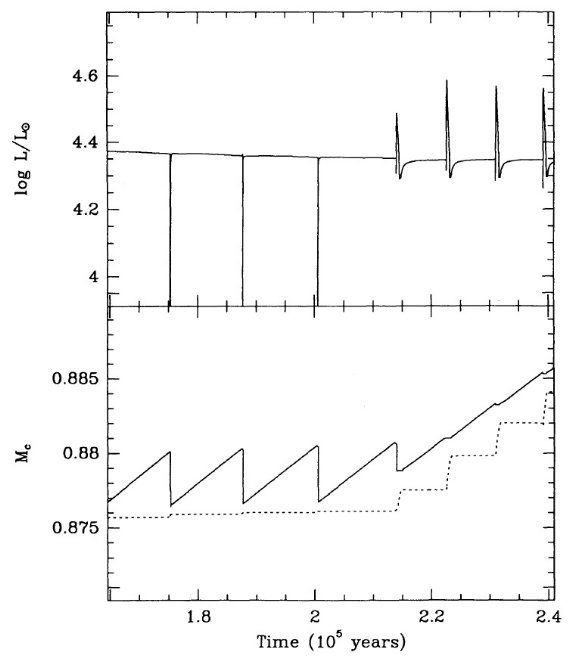
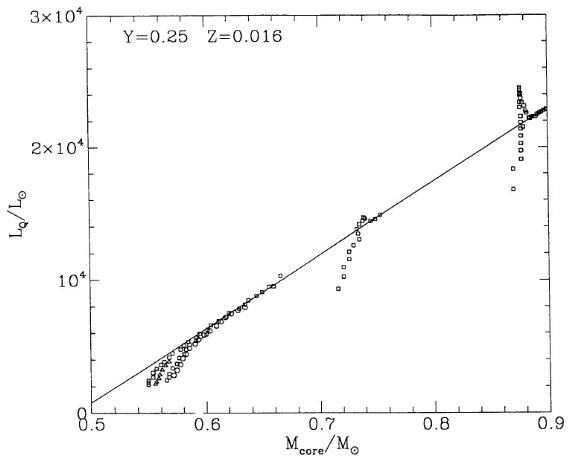
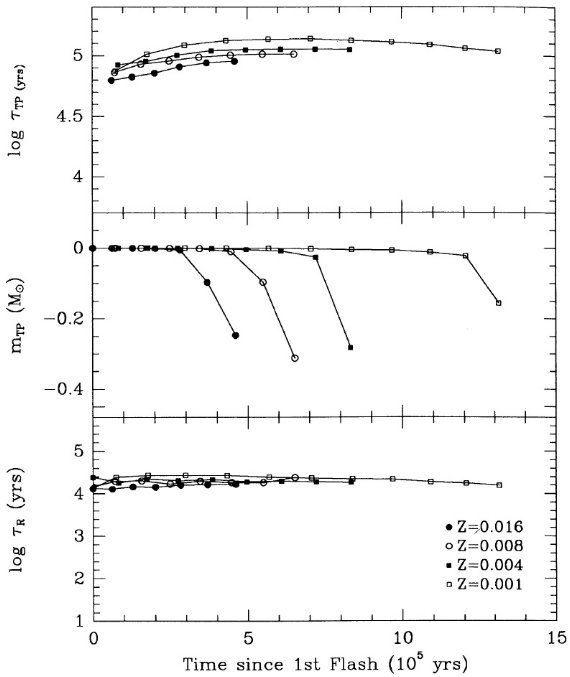
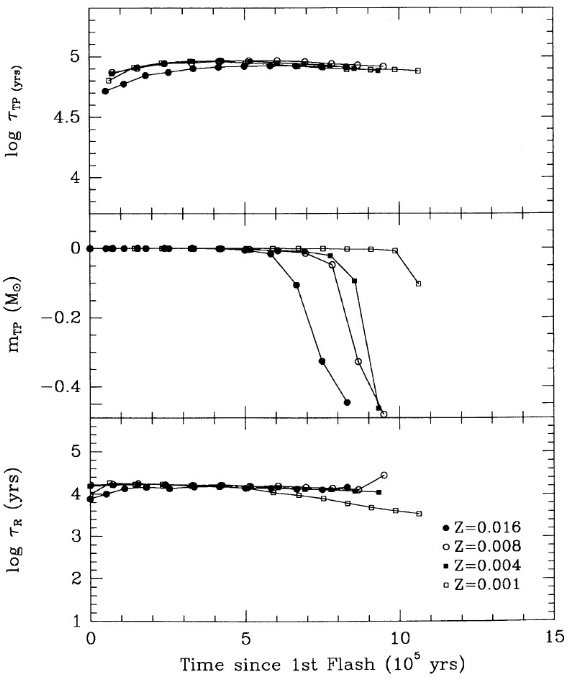
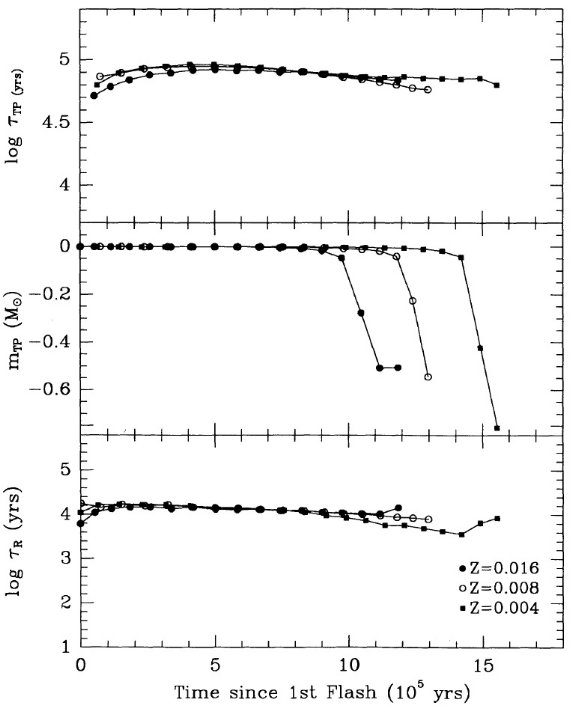
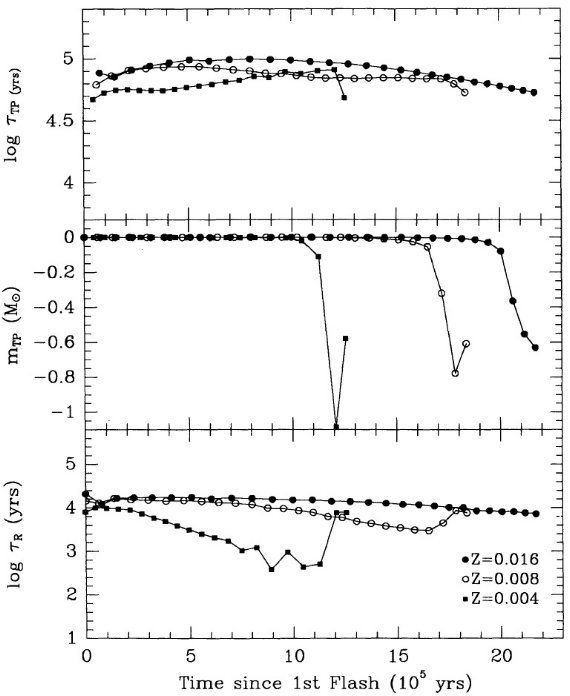
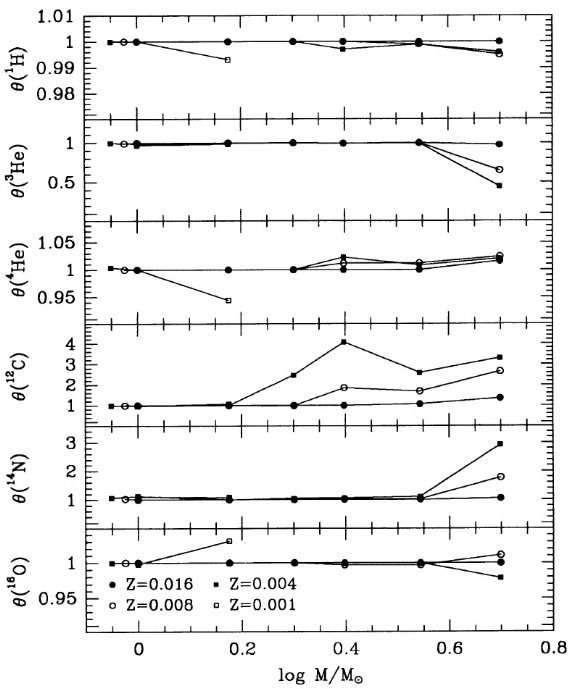
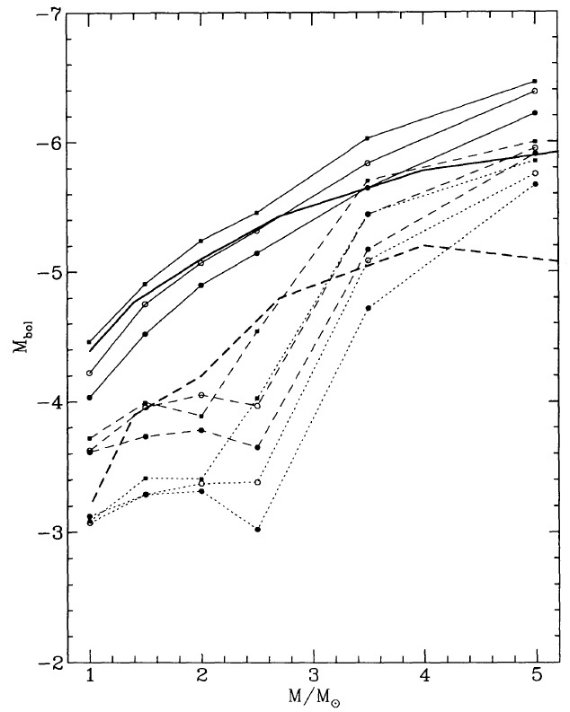
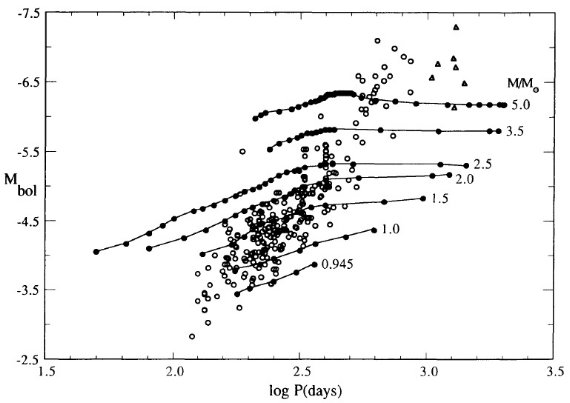
Mount Stromlo Stellar Structure Program　 　ここでの計算は Mount Stromlo Stellar Structure Program を用いて行わ れた。Z = 0.016 はソーラー組成を表す。 Z = 0.008 = (1/2) Zo は LMC, Z = 0.004 = (1/4) Zo は SMC を表す。 N の量はスケールソーラーのさらに 1/2 (LMC), 1/4 (SMC) 少ないことが知られているので、N 量は LMC では 1/4, SMC では 1/16 少ない。 Z = 0.001 モデルも 1/16 ソーラーにした。 Y = 0.25 を仮定した。 　脈動依存のマスロス率　 　マスロスは２段階で、１＝大振幅脈動で物質を上に上げ、２＝そこでダスト が形成されて輻射圧で放出。(dM/dt) - P プロットから、P < 500 d では、 (dM/dt) が P の指数関数的に増加し、 P ≥ 500 d では (dM/dt) = 10-5 Mo/yr の一定値になる。図１にその関係を示す。実線は、 　　　log (dM/dt) = -11.4 + 0.0123 P　　　　　(2) この式は P = 500 d で星がダストに覆われ可視で見えなくなることを予言する。 実際、太陽近傍では Wood, Cahn (1977) が示したように、可視ミラの数が P = 425 - 500 d に掛けて急減する。バルジでも そうである。質量が上がって M = 5 Mo, Mbol = [06, -7] では P = 750 d の可視星も存在する。式 (2) に質量項を加える必要がある。 　log (dM/dt) = -11.4 + 0.0125[P-100(M-2.5)]　　　(5) 5 Mo に対する式 (5) を図１に破線で示した。 　基本振動　 　 Wilson 1982, Wood 1990a,b に従い、ミラは基本振動と考える。Wood 1990a の式 (5) P-M-R 関係によると、P は下の式で与えられる。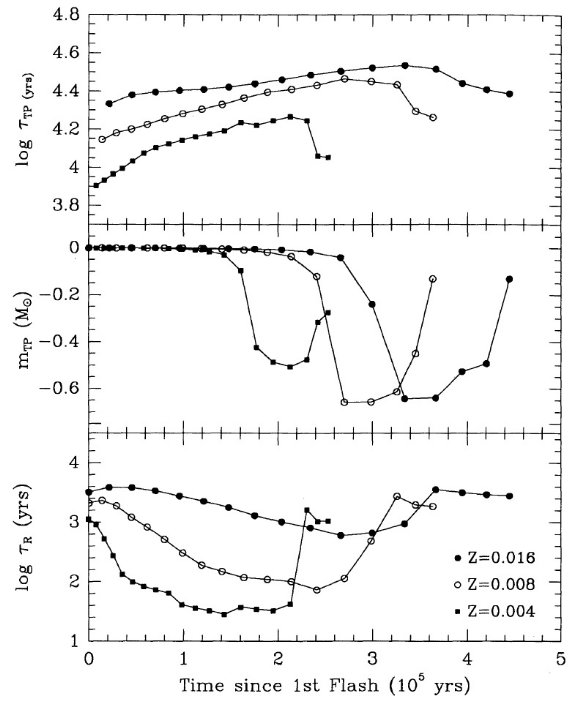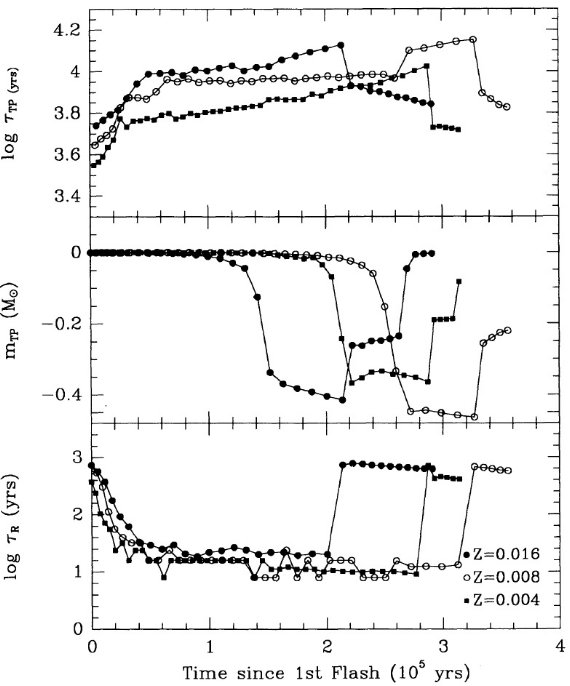 　　　log P = -2.07 + 1.94 log R - 0.9 log M　　　(4) 　Δlog Teff = 0.3 　 　AGB マスロスが完了するのは、外層質量が減ってきて log Teff が参照 AGB 温度に比べ ΔTeff=0.3 高くなった時である。 ここに、参照 AGB 温度は以下の式で与えられる。 　Mbol=12.5logTeff-2.925logM+1.453log(Z/Zo)-47.1　(6) この参照 AGB は進化コードが生む AGB 系列中まだ青側に進化し始める前の部分 である。

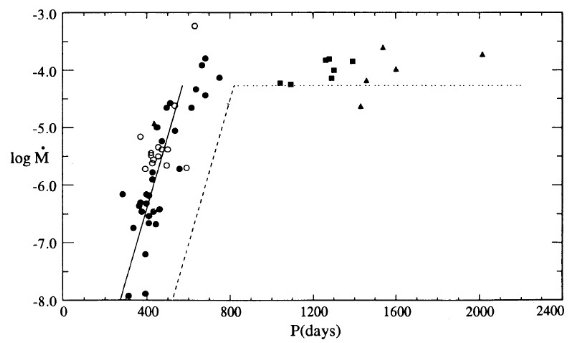
図１．P - (dM/dt) 関係。黒丸＝銀河系 M-, S-型星。白丸＝ C-星。三角＝ OH/IR 星。四角＝ LMC 星。実線＝ M≤2.5Mo 星に適用。破線＝5 Mo 星。 点線＝LMC 5 Mo 星 Mbol = -6.5, vesc = 12 km/s の輻射圧限界。 　第１巨星枝でのマスロス 　 　マスロス式 (2), (5) に使われる周期は、星に式 (6) で決まる Teff を与えて 導かれた。超星風は参照 AGB から ΔlogTeff = 0.3 までの間は保持され ているとした。AGB マスロスは 低-, 中間-質量星では大部分を占める。しかし、 球状星団では、水平枝形態に合わせるためには、第１巨星枝上で 0.2 Mo のマス ロスが必要である。(ただ、 Simon 1992 によればこの確立された 0.2 Mo 損失は 結局のところ不必要かも知れない。) レイマース則を採用すると、マスロス率は R/M に比例する。これらの計算では Mi < 1 Mo の場合のみ FGB マスロスを 考慮した。低質量星で 0.2 Mo の損失を生み出すために η = 1/3 が最適で あることが分かった。詳細は Sweigert, Greggio, Renzini 1990 に述べられている。

　３．結果と議論　

　３．１．熱パルス AGB への進化　

　３．２．熱パルス期 AGB 進化　

図２．(Y,Z) = (0.25, 0.008) の進化経路。 Mi ≥ 2.5 Mo では第１ ヘリウムシェルフラッシュまで、Mi < 2.5 Mo ではヘリウムコア フラッシュまで。

図３．(M,Y,Z) = (0.945,0.25,0.008) の TP-AGB 期進化。横軸は第１熱パルス からの時間。縦点線＝AGN 期終了。M6 = 10-6 Mo/yr 単位のマスロス率。

図４．(M,Y,Z) = (1.0,0.25,0.008) の TP-AGB 期進化。横軸は第１熱パルス からの時間。縦点線＝AGN 期終了。M6 = 10-6 Mo/yr 単位のマスロス率。

図５．(M,Y,Z) = (1.5,0.25,0.008) の TP-AGB 期進化。

図６．(M,Y,Z) = (2.0,0.25,0.008) の TP-AGB 期進化。

図７．(M,Y,Z) = (2.5,0.25,0.008) の TP-AGB 期進化。

図８．(M,Y,Z) = (3.5,0.25,0.008) の TP-AGB 期進化。

図９．(M,Y,Z) = (5.0,0.25,0.008) の TP-AGB 期進化。

　３．２．１．超星風期　

熱サイクルと超星風　 　図３-９の著しい特徴は突然超星風が開始され、 dM/dt = L/cvesc の輻射限界になることである。M ≤ 2.5 Mo の星ではその限界に達するのは 最後の数回の熱サイクルで、超星風同士の間の期間は光度が低下し、マスロス が消えている。もっと重い星では、多数の熱サイクルで限界マスロスが維持さ れる。 　超星風が急に起きる理由　 　超星風前には、マスロス率が周期の指数関数で上昇する。ところで、 P ∝R1.94/M0.9∝L0.97/M0.9 Teff3.88 である。AGB に沿って、L が上がり、 Teffは下がるので P は上がる。マスロスで M が下がると P が 更に上がる。こうして dM/dt は急上昇する。 　間歇的超星風の効果　 　間歇的超星風の効果として、ＡＧＢ星の周りに数個の離れたシェルが存在する。 実際そのような星が見つかっている。 図１０．(M,Y,Z) = (1.5, 0.25, 0.008) 星のマスロスの振る舞い。 曲線１＝進化計算に適用したマスロス率。曲線２＝水素燃焼で失われる質量。 曲線３＝レイマーの公式（η=1/3） 曲線４＝輻射圧限界放出率。

　３．２．２．表面光度の変化　

M < 3.5 Mo　 　低質量星では表面光度変化は他のＺの場合も似ている。各熱パルスの後、短い 500 年くらいの光度パルスがあり、その後サイクル全体の 20 - 30 % に及ぶ 光度低下期が続く。その後光度上昇が起き、次の熱パルスに続く。 　M ≥ 3.5 Mo　 　M ≥ 3.5 Mo では異なる。表面光度は殆ど変化しない。外層質量 Menv < 1.5 Mo まで低下して初めてシェルフラッシュの影響が外に現れる。 その様子は図１１上枠に示されている。 　外層質量が大きいと表面光度の変化が小さい　 　図１１下枠は、何故外層質量が大きいと表面光度の変化が小さいかを示す。 外層が重いと、フラッシュによる表面光度増加は外層対流を引き起こす。 対流は内側に食い込み、コアマスの鋸歯状変化を生み出す。もっと重要なのは 対流の侵入でヘリウム燃焼殻を冷やし、ヘリウム燃焼を止めてしまうことである。 このためにシェルフラッシュが発生する総エネルギーは小さく、表面光度に 影響しないのである。 図１１．(M,Y,Z) = (5.0,0.25,0.016) 星の進化。 上：表面光度の時間変化。下：コアマスの時時間変化。実線＝水素コア。点線 ＝ヘリウムコア。フラッシュサイクルの変化は外層質量の低下による。時間は 第１フラッシュ起点。

　３．２．３．光度 - コアマス関係　

コアマス・光度関係　 　パシンスキー 1970 はコアマスと光度の関係を指摘し、その後の研究で確認 された。しかし、Blocker-Schonberner 1991 は Mi ≥ 7 Mo では L-Mi 関係 が成立しないことを指摘した。彼らはその原因を深い対流層に求めた。同様の 現象は図１２の Mi = 5 Mo の光度が Mc-L 関係の上に来ることに示されている。 外層質量が 4 Mo から 1.5 Mo に下がるに連れ、極大光度は低下して Mc-L 関 係に近づく。その時点で輻射層が水素燃焼層を外挿対流層から分離する。 すると、光度は外層と無関係になる。 図１２．Mi = 1.0, 1.5, 2.0, 2.5, 3.5, 5.0 Mo に対する、静謐期水素燃焼 極大光度とコアマスの関係。直線＝上縁フィット。

　３．２．４．間熱パルス期間と TP-AGB 期間　

図１３．M = 1 Mo 星の、上：間熱パルス期間 τTP、 中：mTP=熱サイクルごとの総質量変化、下：ヘリウムシェルフラッ シュ回復期間 τRの変化。

図１４．M = 1.5 Mo 星の、上：間熱パルス期間 τTP、 中：mTP=熱サイクルごとの総質量変化、下：ヘリウムシェルフラッ シュ回復期間 τR. の変化。

図１５．M = 2 Mo 星の、上：間熱パルス期間 τTP、 中：mTP=熱サイクルごとの総質量変化、下：ヘリウムシェルフラッ シュ回復期間 τR. の変化。

図１６．M = 2.5 Mo 星の、上：間熱パルス期間 τTP、 中：mTP=熱サイクルごとの総質量変化、下：ヘリウムシェルフラッ シュ回復期間 τR. の変化。

図１７．M = 3.5 Mo 星の、上：間熱パルス期間 τTP、 中：mTP=熱サイクルごとの総質量変化、下：ヘリウムシェルフラッ シュ回復期間 τR. の変化。

図１８．M = 5 Mo 星の、上：間熱パルス期間 τTP、 中：mTP=熱サイクルごとの総質量変化、下：ヘリウムシェルフラッ シュ回復期間 τR. の変化。

　３．３．ＡＧＢ先端光度　

Mi - Mbol 関係　 　 Frogel, Mould, Blanco (1990) は LMC 星団 AGB 先端光度を調べた。表２にはモデル AGB 星の性質をまとめた。 Mbolmax(TPAGB) は輻射圧駆動超星風期になる前の可視 期での極大光度を示す。図１９には AGB 期の EAGB, TPAGB の最小最大光度を 示した。太い実線は Frogel, Mould, Blanco (1990) の図１４の (SWB, mbol) = (2, 12.2) と (7, 13.9) を結んだ 線である。また、 彼らの表３にある SWB タイプと初期質量の関係を使った。 LMC 距離指数としては彼らの採用した 18.3 を用いた。18.3 の代わりに 18.5 を用いると、光度は上がるが、ターンオフ光度も上がり Mi が高くなるので キャンセルして Mi - L 関係ではあまり変化しない。 　高質量星の AGB 先端光度　 　図１９を見ると、Mi ≤ 3.5 Mo では観測とモデルの一致が非常に良い。 これは我々が予想する超星風の発現時期と長さが正しいことを支持する。 M = 5 Mo では我々が予想する AGB 先端光度は観測より高い。実際、観測される 先端光度はモデルの EAGB 最大光度に近い。ただし、 3,5 Mo 以上で AGB 期間が急に縮小することを考えると、観測される先端光度がサンプル数が少ない ためかも知れない。 図１９．細実線＝可視 AGB 先端光度。細破線＝ E-AGB 先端光度。点線＝可視 AGB 極小光度。横軸は初期質量 Mi. 黒丸：Z=0.016. 白丸：Z=0.008. 三角：Z=0.004. 太い実線＝LMC 星団の AGB 先端光度。太い破線＝M-C 型星遷移線 ( Frogel, Mould, Blanco (1990) )

　３．４．可視及びダストに包まれた変光星　

AGB LPV の二つの種類　 　AGB 長周期変光星は質量放出率が低く、可視のミラ型変光星と超星風による 高質量放出の最中でダストに覆われた赤外線星を含む。銀河系のそのような 星は van Langevelde, van der Heiden, van Schoonevelde (1990) の OH/IR 星の研究、Wood et al 1992 の LMC 赤外線の研究にある。 今回の研究は AGB LPV が取り得る周期の範囲を限定する。 　モデル周期光度関係　 　図２０には、各ヘリウムシェルフラッシュサイクルにおける最長周期と M bol の関係を示す。各質量で、第１点は第１シェルフラッシュを 示す。周期はもしその光度で振動したらと言う想定で計算されたもので、脈動 安定性の解析は行っていない。初め星は AGB を上がるに連れ、光度と周期を 伸ばして行き、ついに超星風が始まる。そこで周期が大幅に伸びる。 星の質量が大きくなると、超星風の開始に伴う周期の加速は激しい。到達する 最高周期は質量、メタル量と共に増加する。 　LMC LPV の例　 　図２０には LMC LPV (Hughes, Wood 1990, Wood et al 1992)をプロットした。 M ≤ 2.5 Mo 星では可視 LPV は超星風発現前の理論曲線上にある。しかし、 3.5, 5 Mo では可視 LPV が早期超星風の領域に存在する。これ等の星ではまだ 超星風は発現していない。この問題の原因は、図２０での周期は進化計算に現れる Teff を使用して計算されるが、マスロス式に使う周期は参照 CMD の　AGB を表す （６）式で与えられる Teff から計算されるためである。この式の Teff は （多分ログで）進化コードより　0.03 冷たい値を与える。周期 P ∝ Te -3.88 なので、マスロス式に使う log P は図２０で 0.12 大きい値と なる。 Te に対するよりよい解析式を使用していれば、高質量の可視変光星の 周期はもっと長くなる、最終 AGB 光度は &Delata;Mbol = -0.25 等明るくなった だろう。前節で述べたように、我々の決めた AGB 先端光度は既に Frogel, Mould, Blanco (1990) の観測 AGB 先端光度を越えている。可視 LPV の中に明るい光度の星が実在する ことは彼らの AGB 限界光度が暗すぎることを証明している。

図２０．Mbol - log P 関係。実線の P はシェルサイクルの静謐期 極大光度での値。白丸＝可視 LPV. 三角＝ダストに包まれた AGB 星。 　超星風期間　 　表２を見ると、低質量星では超星風期間が TP-AGB 期間の 10 % である。一方 3.5, 5 Mo になると、超星風期間と可視ミラ期間は半々になる。高質量 TP-AGB 星の半分が熱いダストシェルに覆われている事実は LMC で上部 AGB　星が欠けている (Reid, Mould 1985, 1991) という現象の説明に 役立つ。 　説明困難　 　図２０はまた、 1.5 - 2.5 Mo 経路が変光星が見出されるずっと前に始まっ ていることを示す。これは低質量 TP-AGB 星はその寿命のかなりを非変光星と して過ごすことを意味する。逆に、 P < 180 d, Mbol > -3.7 領域にある変光星は TP-AGB 星として説明するのが難しい。これらは静謐極大期 にない暗い星か、 E-AGB 星なのかも知れない。

　３．５．初期・最終質量関係　

表２には星が AGB を離れる時の最終質量 Mf も載せている。 図２１は Mi - Mf 関係を示す。

図２１． 実線＝ Mi - Mf 関係。黒菱＝ log g から 導いた質量。白菱＝星半径から導いた質量。バツ＝連星。

　３．６．表面組成の変化　

第１ドレッジアップ　 　 　第２ドレッジアップ　 　 　第３ドレッジアップ

図２２．θ = (第１ドレッジアップ後組成/初期組成）。ただし、3He 初期組成＝０なので　θ(3He) = 4000×3He 量。

図２３．θ = (第２ドレッジアップ後組成/第１ドレッジアップ後組成）。

図２４．θ = (第３ドレッジアップ後組成/第２ドレッジアップ後組成）。

　４．サマリー