| 主系列から AGB 期を経て、惑星状星雲と白色矮星に至るまでの進化の中で post-AGB 進化を示す。質量放出は惑星状星雲中心星の質量放出の観測結果の 文献値および輻射圧駆動の星風モデルとから導いた質量放出の経験式を用いた。 初期質量 0.89, 0.95, 1.0, 1.5, 2.0, 2.5, 3.5, 5.0 Mo、メタル量 0.016, 0.008, 0.004, 0.001 に対するモデル計算を行った。post-AGB 進化系列は 惑星状星雲中心星が AGB からいつ離れるかによって、二つのはっきりした グループに分かれる。 | 第１グループはヘリウムシェル燃焼が支配的な時、第２グループは水素シェル 燃焼が支配的な時である。計算した２７進化系列中、 17 系列は水素燃焼期、 10 はヘリウム燃焼期に AGB から離れた。低質量モデルはヘリウム燃焼期に離 れることが多く、それはそれ以前の AGB 進化でヘリウムシェルフラッシュ直前 に質量放出が最大となるからである。計算結果を LMC の観測データと較べた。 これ等の計算は惑星状星雲の光度関数を決めるのに有用である。また、楕円星 雲の紫外超過の研究にも役立つ。 |
|
AGB - PN 進化が分かると （１）PNN = 惑星状星雲核 質量 HR 図上の位置と進化計算と比較して、核質量を決める。もし進化計算に マスロスが組み込まれていれば、初期質量が分かる。 （２）星形成史 十分な数の進化経路計算が PN にフィットできれば、Vassiliadis et al 1992 が集めたような PN サンプルから系の星形成史が導かれる。 （３）銀河進化 PNN や AGB は銀河放射の重要な成員であるので、銀河進化の研究には その正確な評価が重要である。とくに PNN は UV 光に寄与大である。 過去の PNN 計算 Paczynski 1971 は PN の観測的な Harmon-Seaton 系列が、様々な質量の PNN 進化系列の重ね合わせであると指摘した。過去２０年、PNN 計算は、 Paczynski 1971, Schonberner 1979, 1981, 1983, Wood, Faulkner (1986) など が行った。Paczynski 1971 計算はヘリウムシェルフラッシュを人為的に抑え、 マスロスも考慮されなかった。あまり良いモデルとは言えないが、他に同等品が 無いため 0.6 - 1.2 Mo 星のモデルとして広く引用された。Schonberner 1979, 1981 計算は He シェルフラッシュを扱った最初のモデルで、マスロスにはレイマ ースの式が採用された。ただ、最近の Knapp 1986, Wood 1986 の観測は実際の マスロスがこの式の数ケタ大きいことを示している。Schonberner 1983 は 高いマスロスを AGB 期の最後に加えた。しかし、それは進化モデルの最初の 2 つの初期質量に対してのみであった。 Wood, Faulkner (1986) はコアマス 0.60 - 0.89 Mo で Schonberner 計算 0.546 - 0.644 Mo に比べると、範囲 が広く、高マスロスの効果も調べている。彼らはまた、PN 噴出が起きる時の ヘリウムシェルフラッシュ位相が PNN 進化に及ぼす効果を系統的に調べた。 ただし、 PNN 経路が初期質量 2 Mo モデルから様々な量の質量を剥ぎ取って 初期 PNN モデルにして始めたという欠陥がある。 |
PNN 星風 マスロスが PN 期にも起きるなら、そして幾つかの PN では実際にマスロスが 観測されているが、PNN 進化速度に大きな影響を持つ。全てではないが、多くの PNN で質量放出が観測されている。 Mendez et al 1988 はエディントン 限界光度近くでは星風が観測されることが多いと述べている。PNN の有効温度と 星風速度の間には強い相関がある。これは輻射駆動星風で期待される関係である。 星風速度は典型的には 1000 km/s である。質量放出率は AGB 最終期の放出率 の３桁ほど低い。 AGB から PN へ AGB から PN への変化は低速高密度星風から高速希薄星風への転換を伴う。 この変換メカニズムは不明確でそのため AGB から PN 期への遷移期間はまだ 明らかでない。モデル計算では遷移期間を 1000 年とした。PN の流体力学モ デルはそのような計算に依存している。つまり不定性は解消していない。 PPN 最近、 Pottasch, Partharasathy 1988, Hrivnak, Kwokm Volk 1989 は赤外 超過を持つ A-F 型超巨星を発見した。それらは PPN と名付けられ、AGB 期の 厚いダストシェルが光学的に薄くなり、中心星が見えてきたものと考えられて いる。従ってこのような天体は AGB から PN への移行期にあると考えられる。 今回のモデル 今回の計算の初期モデルは Vassiliadis, Wood (1993) から採った。そのモデルは主系列から AGB 終末期まで、観測的マスロスを付け て計算された。このため、ヘリウムシェルフラッシュの回数は現実により近く なった。銀河系、マゼラン雲での PNN 進化を考慮して、メタル量の異 なるモデル計算が行われたのも新しい点である。 |
PNN 進化計算には Mount Stromlo Stellar Evolution プログラムが用いら
れた。 AGB から PN への遷移期間中でのマスロスは進化の決定的要因である
が、マスロスのデータは殆どない。本計算では、マスロス式を用いた。
２．１．星風最終速度理論は v∞ が vesc と共に増加することを予言 する。PNN が進化すると半径が小さくなり、 vesc が、増加する。 我々は Pauldrach et al 1988 が集めた PN データから、 Teff と vesc∞/vesc) と Teff の関係を図１に示した。(キャプションと違う。どうしてか？) AGB - PN 間では A - F 超巨星の観測が重要である。それらや B 型星も図１に示す。 図１のフィットは log(v∞/vesc) = -2.0 + 0.52 lof Teff 図１．（観測星風最終速度/恒星表面脱出速度）対有効温度。点線＝PNN 星風モデル（Pauldrach et al 1988）。上から 0.546, 0.565, 0.644, 1 Mo. 黒丸＝ Pauldrach et al 1988 観測。log Teff = 3.5 付近のバツ＝ OH/IR 星の平均。三角＝ B 型星。四角＝ A - F 型超巨星 (de Jager et al 1988) 実線＝観測点のフィット。 |
 |
|
PNN の質量放出には大きな不定性がある。研究によってファクター 10 - 100
の違いがある。 (dM/dt)lim = L/cv∞ は (うーん、何が書いてあるのか？) 図２．(dM/dt)/(dM/dt)lim 対 Teff の関係。(dM/dt)lim = エディントン限界質量放出率。点線＝ Pauldrach et al 1988 の理論曲線。 質量は図１と同じで、下ほど高質量。白丸＝Hutsemeker, Surdej 1989 観測。 四角＝Perinotto 1989 データ。Pauldrach et al 1988 の分類に従い、 黒印は He 正常 PN、白印＝ 高 He PN. 実線でつないだのは同じ天体の 異なる観測。破線＝輻射圧駆動型星風の理論限界。 実線＝理論的情報のみの平均。 |
 |
|
PNN 進化経路を計算した Vassiliadis, Wood (1993) の AGB 22 系列から PNN 27 系列を計算した。内、 PNN 17 系列は H 燃焼、 10 系列は He 燃焼である。追加の 5 系列は、AGB 最後の 2 - 3 ヘリウム シェルフラッシュサイクルの間のマスロス率を少し変えて、希望する位相 で AGB から離れるようにした計算である。残りの 22 系列は AGB 計算で 使われたのと同じマスロス率を使用した。それらの系列では AGB からの 離脱は AGB 進化の最中のマスロスの自然な帰結である。 離脱位相 φT この論文では、 離脱位相 φT = AGB マスロスが止まり、 PNN マスロスが 開始する時点と定義する。この転換が起きる温度を (logTeff)T とする。Kwok,Volk, Hrivnak 1989 は 非脈動の OH/IR 星の SED から 星が 5000 - 7000 K になる前に AGB マスロスが停止するとした。 (5000 K じゃ意味ない！ それとも そこまで AGB マスロスが継続と言うことか？) H-燃焼と He-燃焼型 PNN PNN 進化経路は HR 図上の形態で H-燃焼型と He-燃焼型とに二分される。 それぞれの出発点と光度低下タイムスケールは表１と２に示す。フラッシュ間隔 時間 tcyc は Vassiliadis, Wood (1993) から採った。以下の式で表される。 log tcyc = 7.47 - 0.49(Z/Zo) + (-3.98+0.52 Z/Zo)(Mc/Mo) |
コアマス・光度関係, コア質量・初期質量関係 表１、２から PNN のコアマス・光度関係, コア質量・初期質量関係を出すと、 L/Lo = 56694[(Mc/Mo)-0.5] Mc/Mo = 0.473 + 0.084(Mi/Mo) - 0.058 log(Z/Zo) 図３−９＝PNN 経路。メタル量別。 図３−９には log Teff = 4 から先の進化経路が Z = 0.016, 0.008, 0.004, 0.001 の順に示されている。表３、４はそれらの (log L/Lo, log Teff) を示す。 He-燃焼の場合 PNN は何度か高温となるが、その ループは示されていない。log Teff = 4 となる時のフラッシュサイクル位相 ψ4 が最後の通過となる。 |
 図３．H-燃焼型 PNN 進化経路。Z = 0.016. 括弧内左＝初期質量。 括弧内右＝ Teff=4 にときのコア質量。水平部の目盛＝１００年単位。 t = 1000 年以降は 1000 年単位。黒丸＝ 10 万年。 |
 図４．図３と同じだが、Z = 0.008. Dopita, Meatheringham 1991 a, b の LMC PN 観測点を加えた。黒丸＝可視で厚い天体。白四角＝タイプI PNs. バツ＝可視で薄い天体。Mi = 1.5 Mo 経路は実際は H-燃焼経路だが、非常に 遅い He フラッシュをくらい、その後 H-再燃焼が起きなかった、 |
 図５．図３と同じだが、 Z = 0.004. |
 図６．図３と同じだが、 Z = 0.001. |
 図７．図３と同じだが、 Z = 0.016 He-燃焼 PNN. |
 図８．図７と同じだが、 Z = 0.008.LMC PNs データを足した。点の説明は 図４参照。 |
 図９．図７と同じだが Z = 0.004 |
|
遷移時間（transition time）ttr 遷移時間（transition time）ttr (Renzini 1989, Schonberner 1990)は、PNN マスロス活発化＝ AGB 点から ΔlogTeff = 0.3 離れる、から log Teff = 4.0 になるまでに掛かる時間である。この時間は期間中のマスロス 率という不定要素で決定されるために、全く不確定である。表１、２には各進 化経路毎に遷移時間の値を示した。 (遷移時間はどう決めたのか？) この値は本来、AGB 計算と PNN 計算をつなげる役割をする。表を見ると、 遷移時間は 3000 年から 20,000 年の間に散らばる。遷移時間と初期質量 Mi の 間に相関はない。遷移時間は遷移期マスロス率と共に離脱位相 φT にも影響される。遷移点で dM/dt は AGB の 10-5 Mo/yr から PNN の 10-7 Mo/yr に転落する。図１０にはその様子を示す。マスロス率の 転換は B 点で起きている。 マスロスと H-燃焼浸食 図１０，１１，１２にはマスロス率に関する他の特性の時間変化も示されて いる。PNN 期の大部分で H-燃焼による外層浸食は我々の計算でのマスロス率、 それ自体は η=1/3 レイマース則より大きいのだが、を上回っている。 唯一例外はプレＰＮ早期で、この時期だけはマスロスが H-燃焼浸食より速い。 われわれのモデルは、例えば Schonberner のような、低いレイマース則を使用 したモデルより、進化が速い。 He-燃焼経路 He-燃焼経路の場合はもう少しややこしい。 5000 年くらいの速い、青い方向 (log Teff)max = 4.6 のループ (Iben 1984, Wood, Faulkner (1986) が起き、その後しばらく AGB に復帰するという現象が起きる。もしも、帰還 時に ΔlogTeff < 0.3 であるなら、我々のモデルでは高い AGB マス ロスが復活し、外層質量がより速く減少するために、進化が速まる。 PNN マスロスは、その後 ΔlogTeff > 0.3 となった時に復活する。 これは図１２のＢ点で示されている。その後の進化では、適用されるマスロス は、レイマース則よりも、また H-燃焼浸食よりも大きい。その大きさは 対応する図１０の (Mi, Z) = (1, 0.016) H-燃焼進化の場合よりも大きい。 しかし、ついには H-燃焼が復活し、 H-燃焼外層浸食が外層質量減少の主因と なる。 |
 図１０．実線＝(Mi, Z) = (1, 0.016) H-燃焼 PNN の質量放出率の時間変化。 点線＝輻射圧駆動限界質量放出率。破線＝レイマースの式。一点破線＝H-燃焼 による外層浸食率。Ａ点＝最後の He フラッシュ。Ｂ点＝ＡＧＢ星風から PNN 星風への切り替え。Ｃ点＝ PNN が到達する最高温度。 |
 図１１．図１０と同じ。ただし、(Mi, Z) = (5.0, 0.016) H-燃焼 PNN. Ａ点とＢ点は図のＸ軸範囲から外れる。 |
 図１２．図１０と同じ。ただし、(Mi, Z) = (1.0, 0.016) He-燃焼 PNN. |
|
ダイナミカル時間と遷移時間 前にも述べたが以前の研究、Schonberner 1983, Wood, Faulkner (1986) ではマスロスを調整して、遷移時間を 5000 年くらいにしていた。これは観測 で決まる惑星状星雲のダイナミカル時間＝R/Vexp に合わせるためであった。 しかし、 Dopita et al 1987, Dopita, Meatheringham 1990 はマゼラン雲 PN の膨張速度が初期の水平枝期には加速しているが、光度低下期には一定速度 になることを示した。これは、ダイナミカル年齢が経過時間の下限値を与える だけであることを意味する。 |
ダイナミカル時間の散らばりの意味 我々の計算が正しい遷移時間を与えているかどうかは分からないが、観測か ら得られるダイナミカル時間 Sabbadini 1986 は 100 - 10,000 年という広い 幅に散らばっている事は面白い。この散らばりは我々の計算でも見られる。 観測データからは星雲年齢と光度の間に相関がみられない。これも、AGB 離脱 の位相が均一に散らばっていると考えると理解できる。 |
|
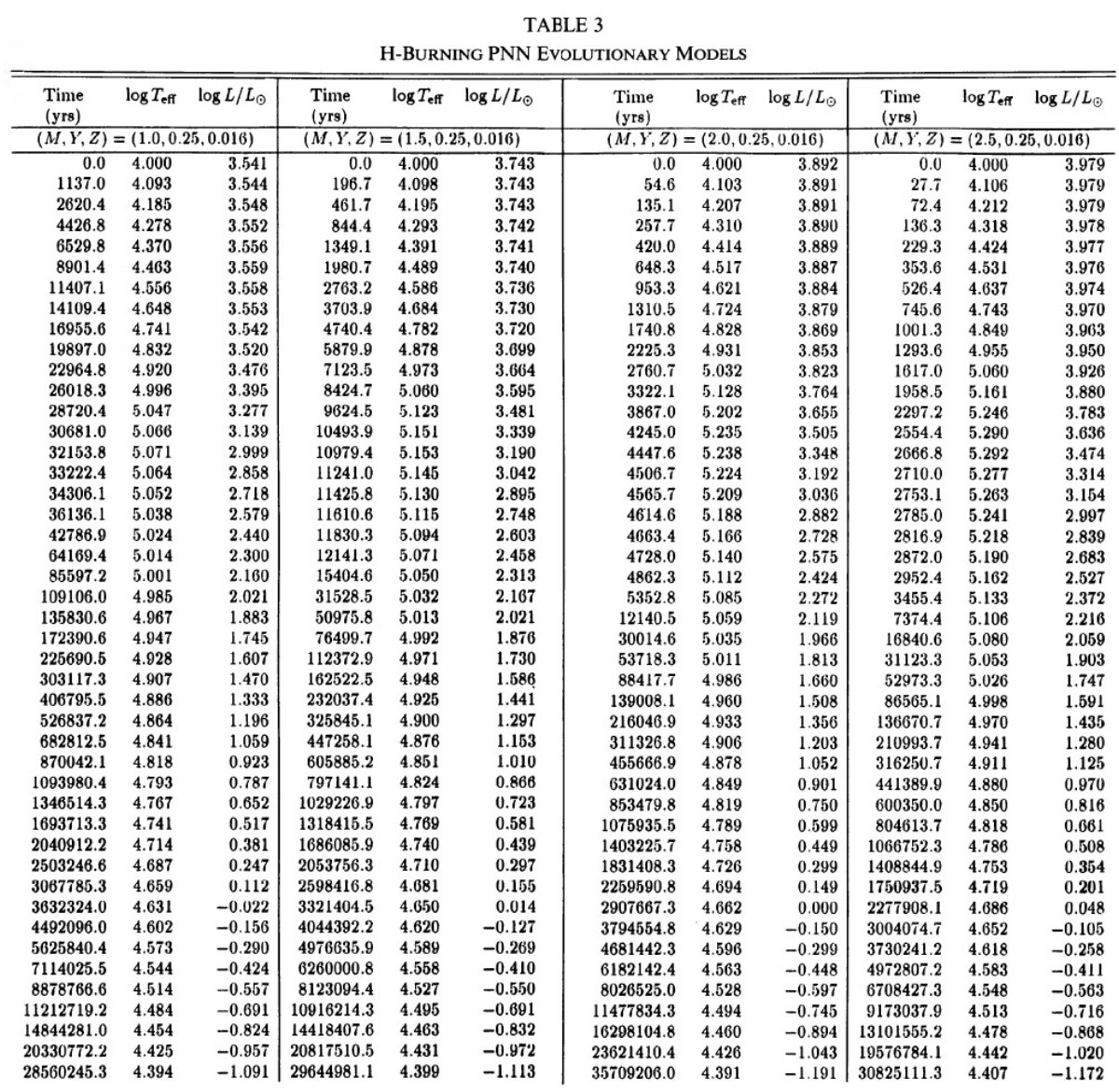
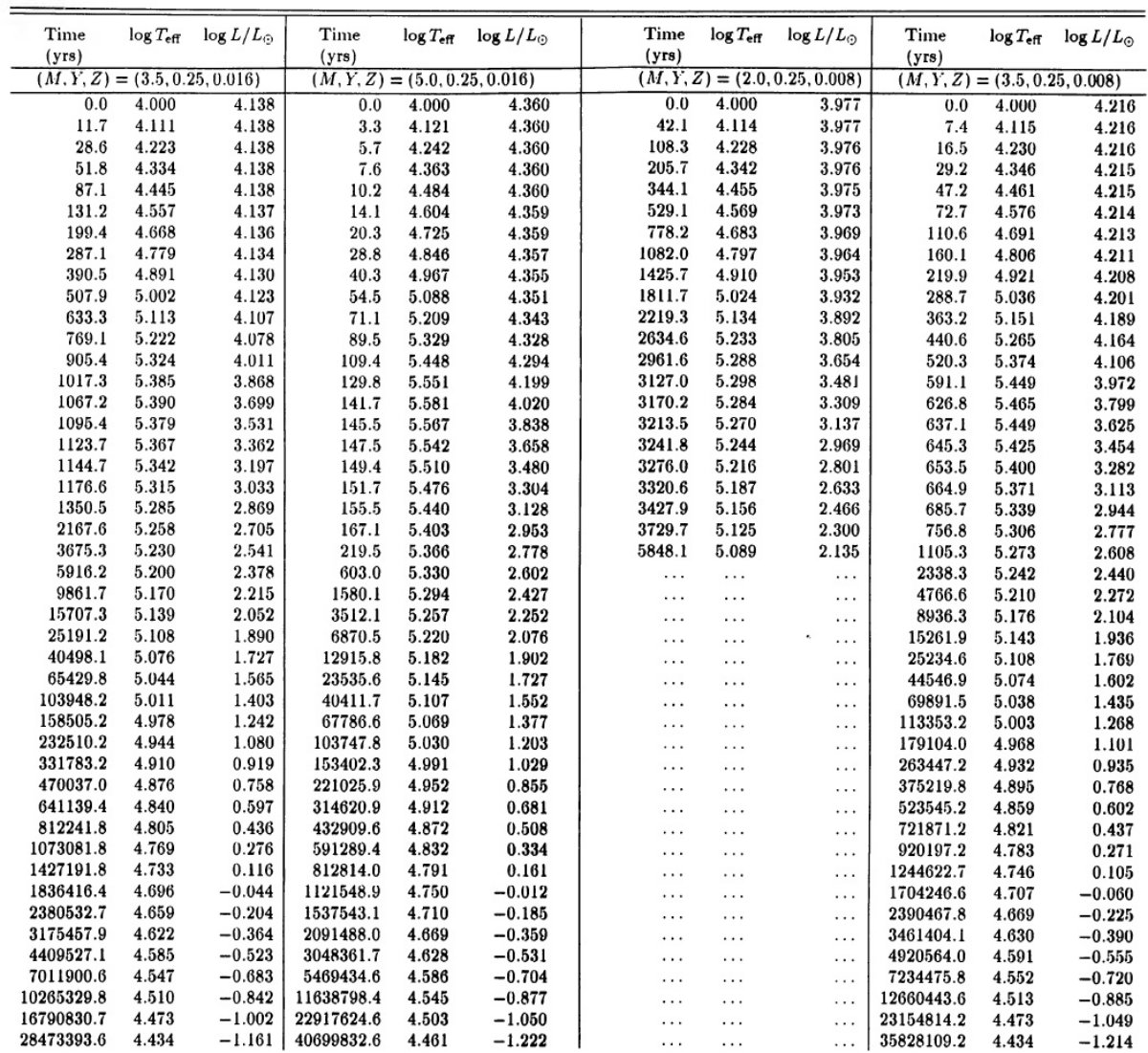
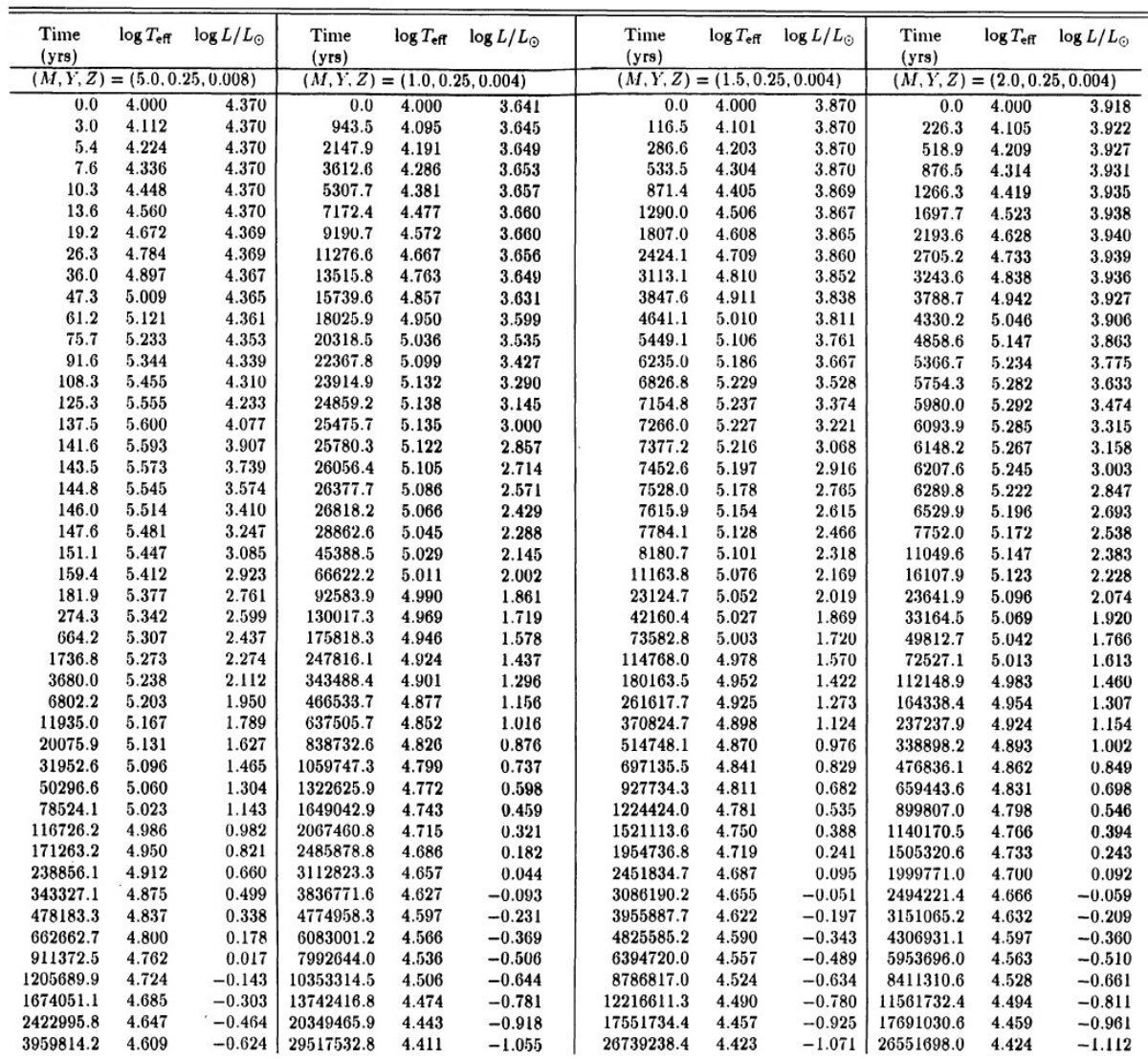
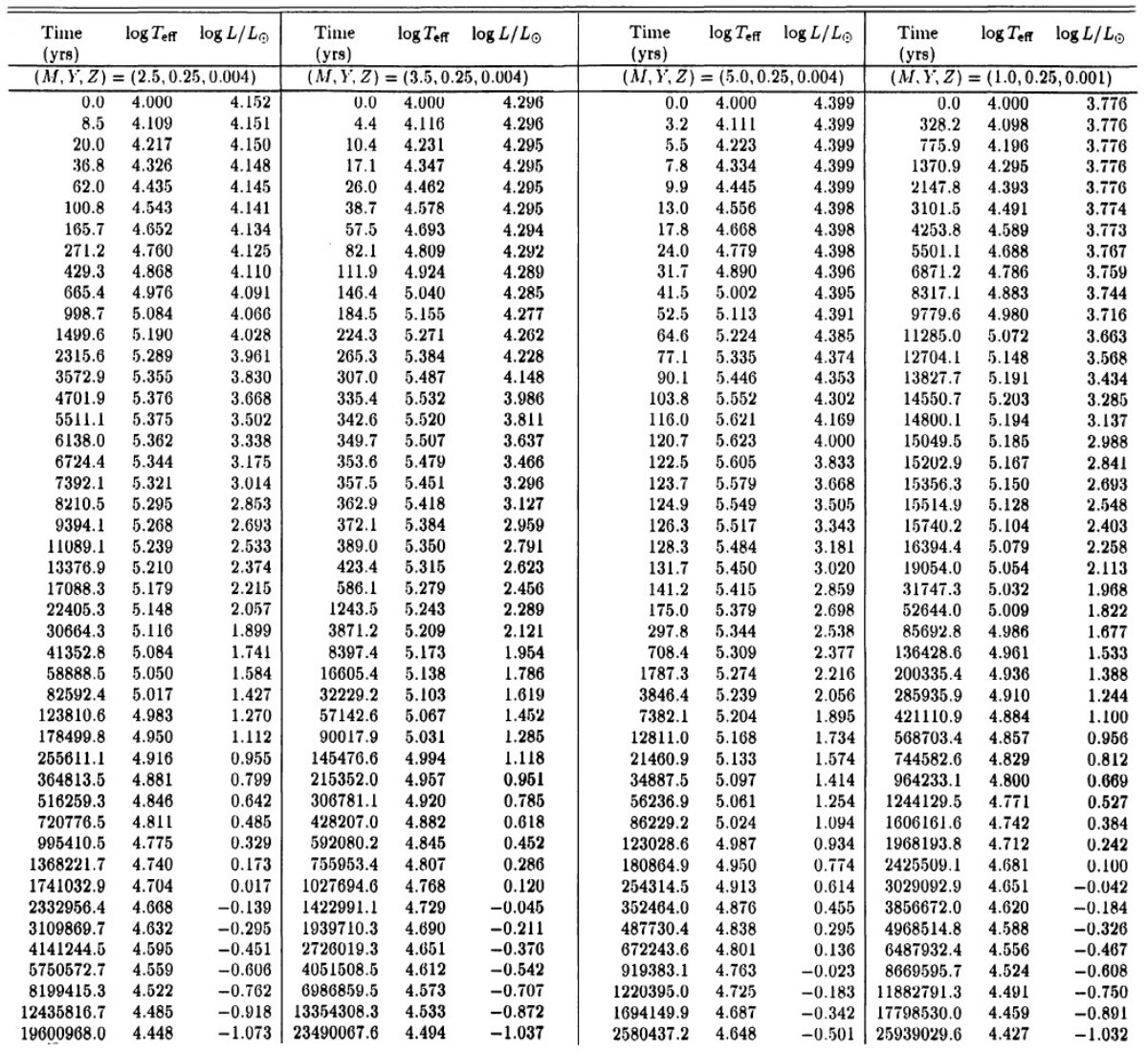
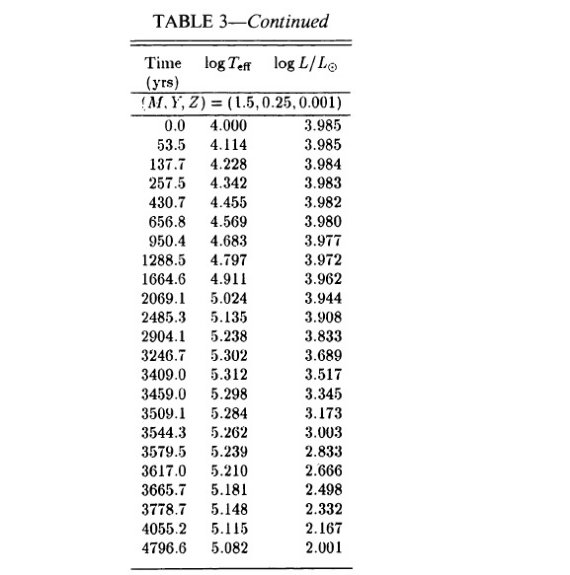
高質量 PNN M ≥ 0.8 Mo PNNs の進化は速いので、我々が高質量 PNN を実際に観測で きるのは、低光度になってからである。0.9 Mo H-燃焼 PNN モデルでは、進化 速度が緩むのは log L/Lo = 1.8 - 2.0, で log Teff = 4.0 から 10,000 年 経っていた。PNN 質量が増加するにつれ、10,000 年後の L は下がって行く。 Blocker, Schonberner 1990 Blocker, Schonberner 1990 は 0.836 Mo PNN が 10,000 年後も log L/Lo = 2.5 でかなり明るいことを示した。また、PNN 質量が上がると 10,000 年後の 光度も高いことを見出した。その結果として、観測される最も暗い PN は低質量 PNN で、以前考えられていた暗い PN は高質量 PNN とは逆であるとした。 この結論は我々や Wood, Faulkner (1986)、 Paczynski 1971 と反する。計算パラメタ―の違いとしては、我々の方が彼等 より小さいマスロスを採用していることくらいである。なぜ結論が変わるのか 検討が必要である。 タイプ I PN の年齢 Peinbert 1978 のいうマゼラン雲タイプ I PN (＝ 高 He, N) はモデルと観測 の比較に向いている。分光測光観測と電離モデル(Dopita, Jacoby, Vassiliadis 1992, Dopita, Meatheringham 1991b)から、それらは HR 図上で M > 0.7 Mo の領域に位置する。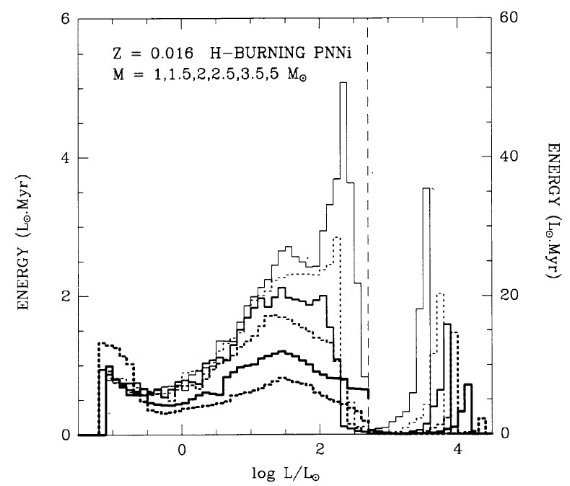これらは高質量 AGB 星で強い第３ドレッジアップと多分 外層燃焼を受けたものの子孫であろう。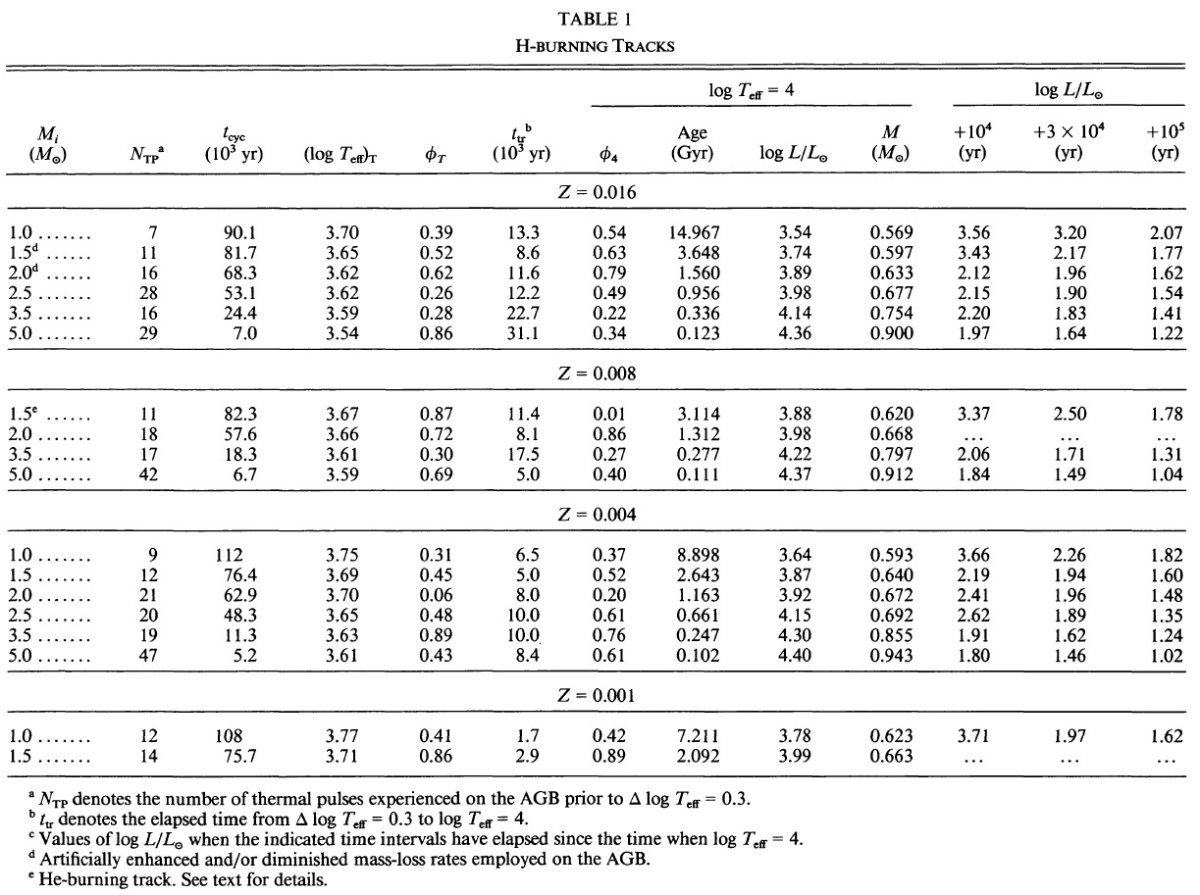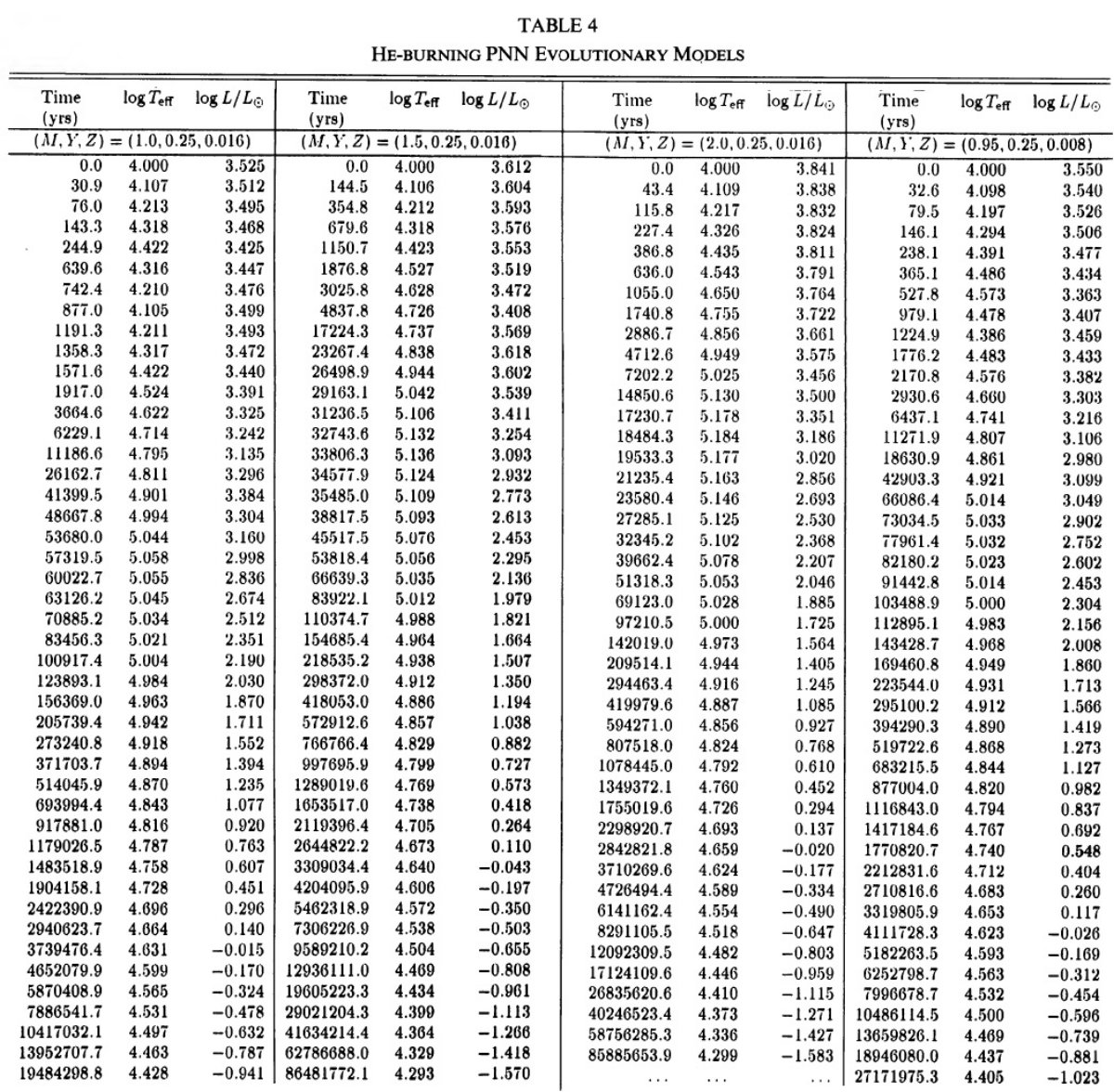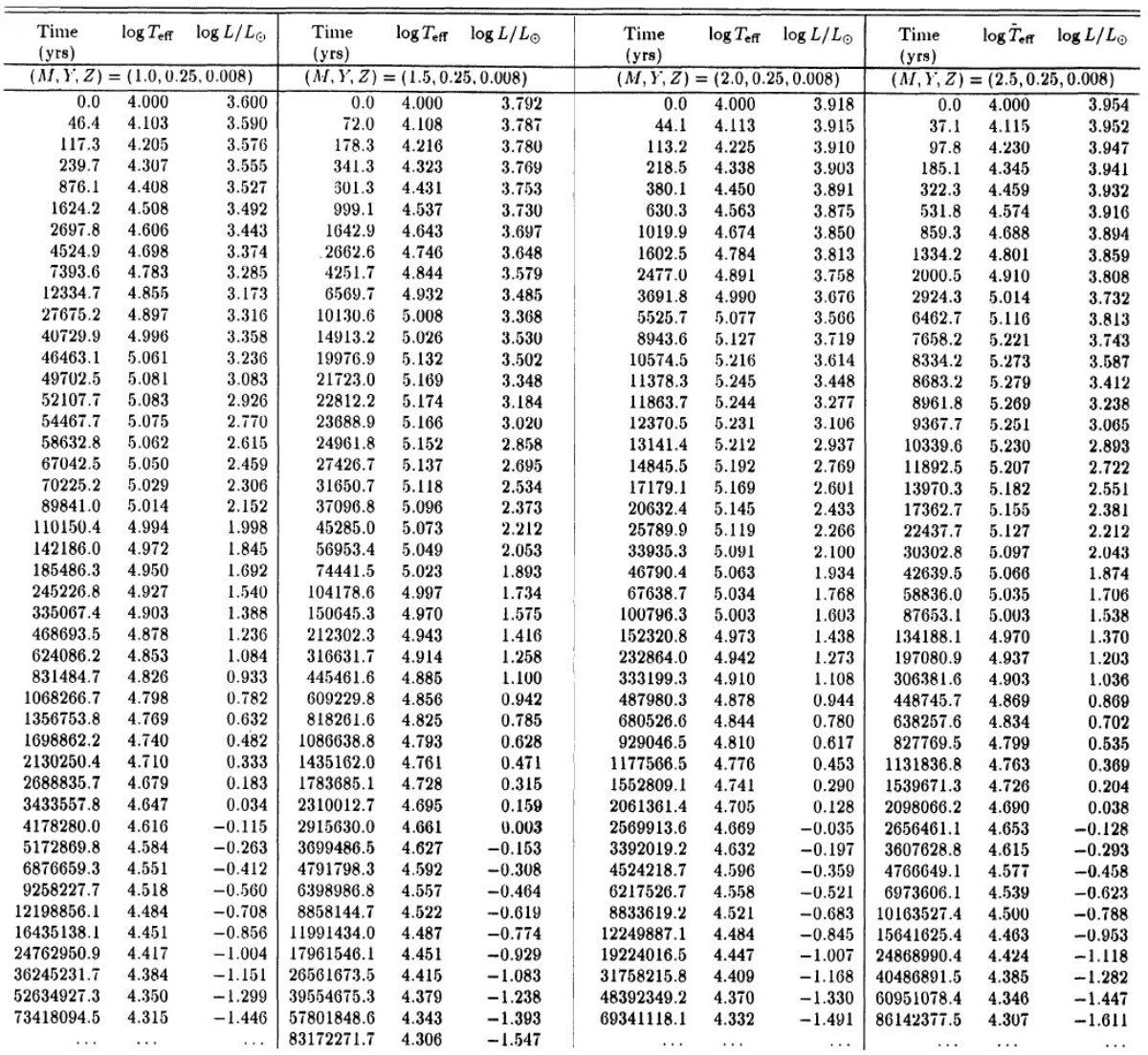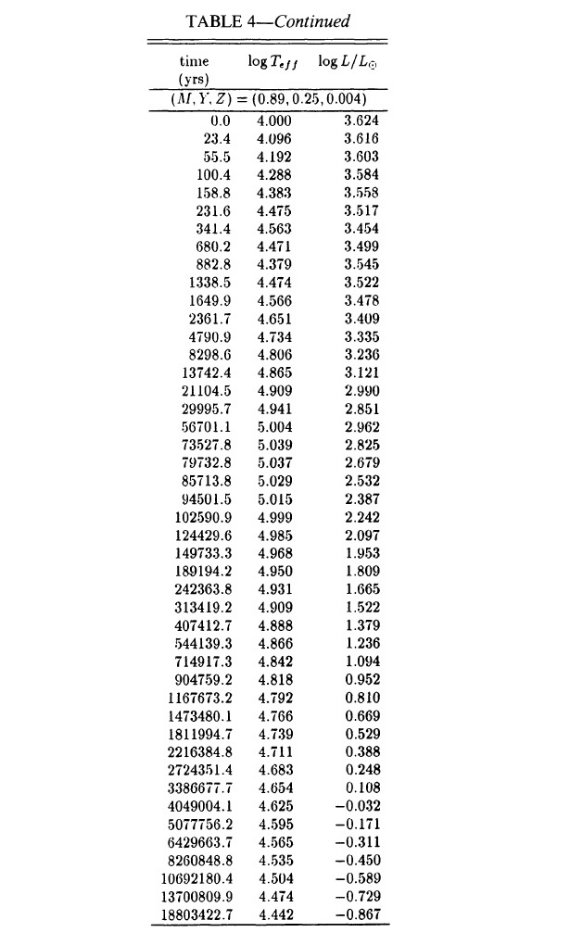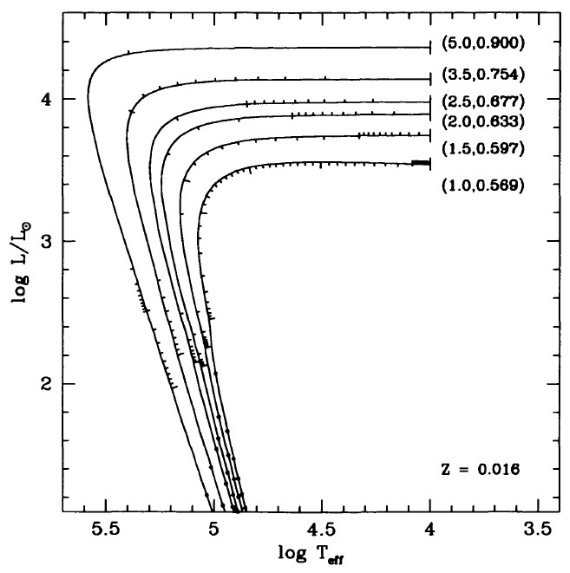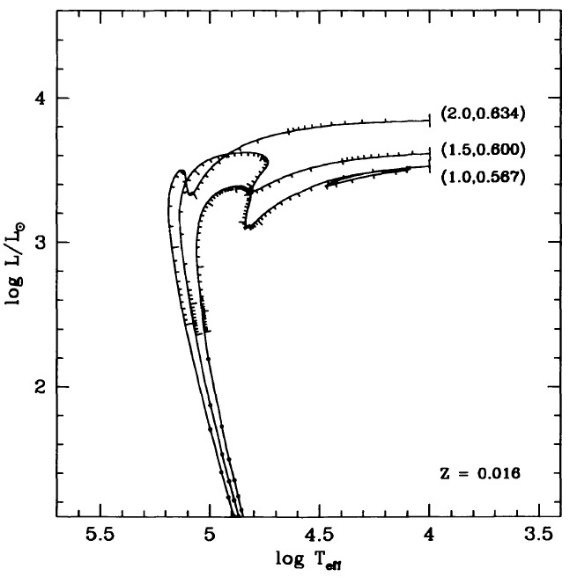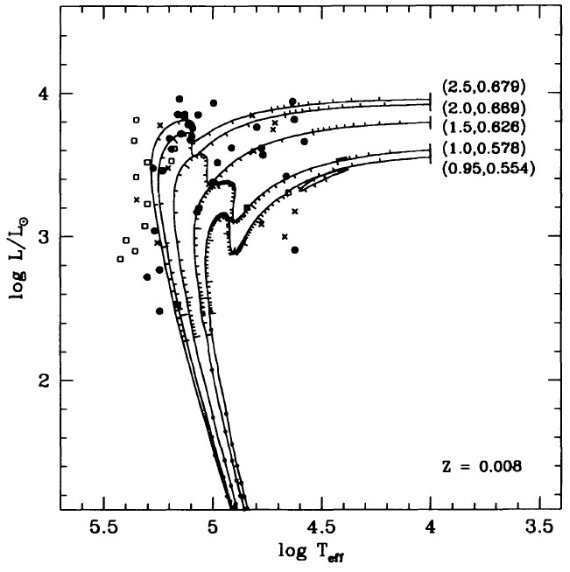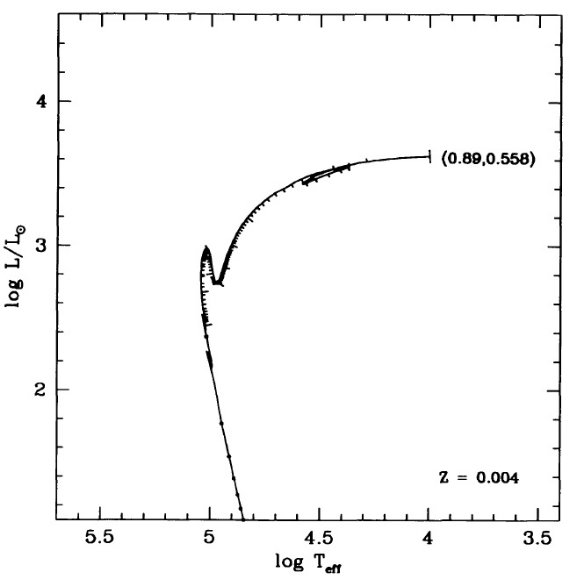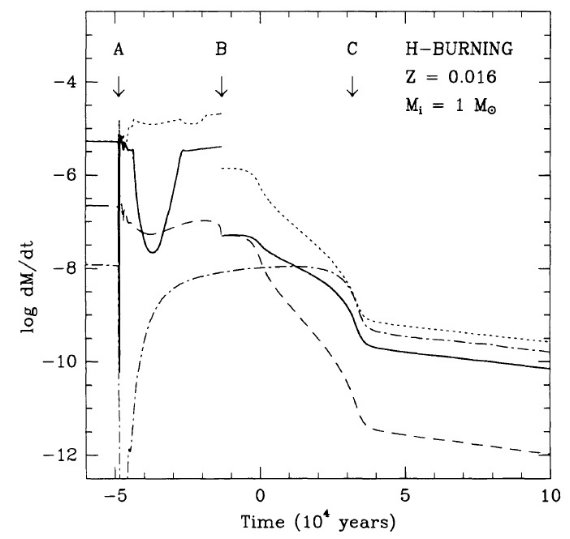LMC タイプ I 天体の光度は log(L/Lo) = 2.5 - 4 に亘る。図４で水素燃焼経路と較べると、この区間は非常に速い進化 期にある。単一の t = 1000 年等時線が観測点の大部分にフィットするようだ。 しかし、これはサンプル天体のほぼ全てが、全質量に亘って非常に若く、コンパ クトで、1000 年前には log Teff = 4.0 であったことを意味する！タイプ I PN がそのような狭い年齢帯に集中して存在することは考えにくい。 |
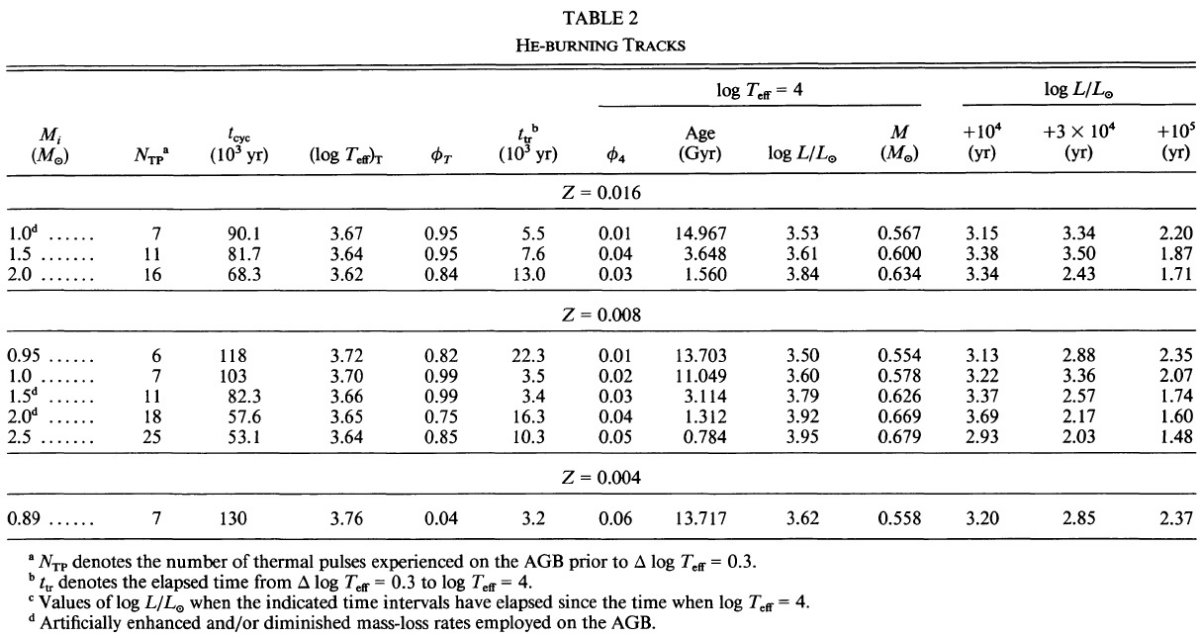
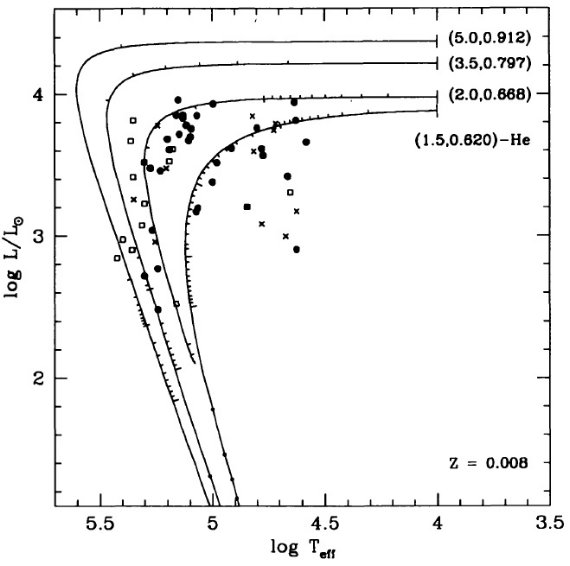
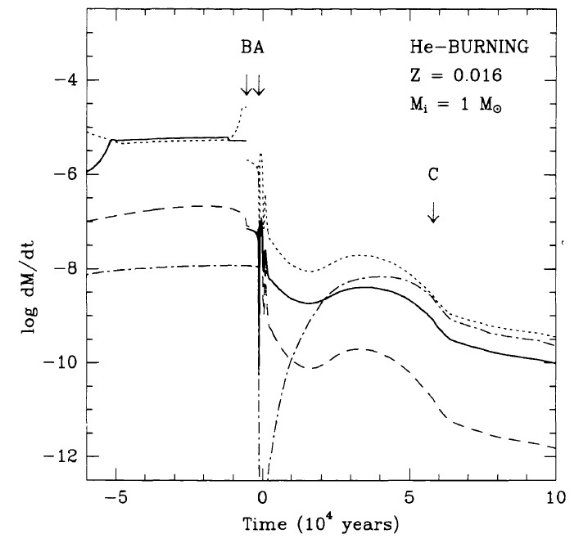
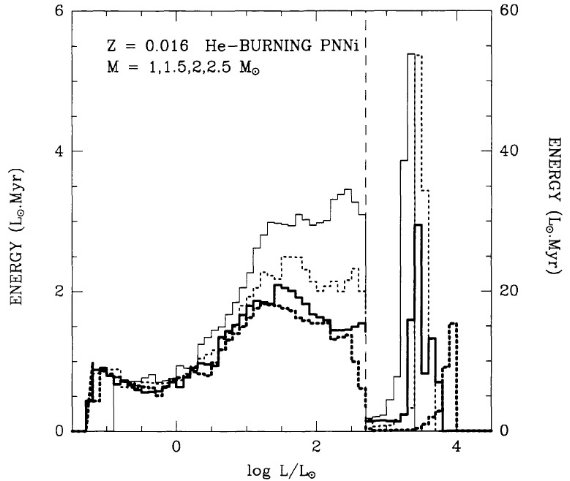
ヘリウム燃焼タイプ I PN 図８はヘリウム燃焼 PNN だと log L/Lo = 2.5 - 4 区間に数千年滞在する ことを示す。図４の結果と較べると、タイプ I PNs はヘリウム燃焼で PN 領域 に入るようだ。水素燃焼 PN はあるかも知れないがこの領域は高速で通過する ので観測には掛からないだろう。 Wood, Faulkner (1986) が提案した、 Mi > 5 Mo,Z=0.016 での He-フラッシュ時の輻射圧による外 層放出による AGB 離脱メカニズムがヘリウム燃焼によるタイプ I ＰＮを説明 できるかも知れない。 高マスロス星の死亡率１ より高質量のタイプ I PNs が全てヘリウム燃焼星として PN 領域 に入るのか、選択効果＝高光度の結果多数の log L/Lo < 2 の水 素燃焼星を見逃しているのかが問題で、これ等の星の死亡率を調べ なくてはいけない。タイプ I PNs の前駆星はおそらく高質量 (5 Mo), 高光度 Mbol = [-7, -6] ダストに埋もれた脈動 IRAS 天体であろう。 Wood et al 1992 はそれらの 8 個を LMC で観測し、マスロス率を 10-4 Mo/yr とした。それらの星が 4 Mo 質量を失うと すると、超星風期間は 40,000 年である。これから LMC 全体での 死亡率として 1 天体/5000 年となる。 死亡率２ マスロス AGB 星の前駆星は可視長周期変光星 Wood, Bessell, Fox (1983), Hughs, Wood 1990 であろう。LMC 内には Mbol = [-7, -6] の可視 変光星が 30 ある。それらは、 P > 500 d で、Mi ≥ 5 Mo である。 そのような LPV の寿命は良く分からないが、 Hughes, Wood (1990) はもっと低質量 LPV に対して 5 万年という評価を出した。熱パルス期にある AGB 星全てが脈動しているわけでない。可視で見える期間の 10 - 20 % が ミラとして脈動している。 Vassiliadis, Wood (1993) 表２の可視期間から我々の AGB 計算は Hughes, Wood (1990) のミラ寿命と合っている。AGB 先端ではコアマス増加がヘリウムシェルフラッ シュ二より抑えられるので、光度増加も 0.01 mag/5 万年と遅い。なので、 ミラの寿命が 5 万年より短いことは考えにくい。この値を使うと、これらの 天体の死亡率は 1/2000 年 となる。 |
|
タイプ I PN を水素燃焼とすると寿命が短すぎ 上の二つの寿命から、タイプ I PN は LMC 全体で 1 星/ (2000 - 5000) 年 の割で誕生している。図４を見ると、 log(L/Lo) = [2.8. 3.8] に８個のタイ プ I PN がある。もしこれらが水素燃焼星だと、仮にコアマスを 0.67 Mo と 低く見積もってもそこでの寿命は 1000 年、もっと現実的に Mbol = -6 に 対応する 0.9 Mo としたら 100 年以下になってしまう。そのような寿命では、 死亡率 1 星/250 年（125 年じゃないのか？）もっとありそうな値は 1 星/12 年となる。これは、前駆天体としての AGB 星死亡率と食い違う。 これに反し、図８はヘリウム燃焼 PNNs がより長い寿命を持つことを示す。 残念ながら高質量 (0.9 Mo) ヘリウム燃焼 PNN モデル経路が計算できない。 しかし、より一般的な 0.67, 0.68 Mo ヘリウム燃焼 PNNs は log(L/Lo) = 2.8 より明るい区間に 4000 年滞在する。これは水素燃焼核の 4 倍長い。 すると 4000/8 = 500 年に 1 星のタイプ I PN 死亡率となり、 AGB 死亡率 と近い。 |
タイプ I PN 候補巾を広げる ヘリウム燃焼だけでは AGB と タイプ I PN の死亡率の差は埋まらない。 最も良い解決は前駆 LPV 天体の質量巾を広げることである。最も明るいタイプ I PNs は log L/Lo = 3.8 (Mbol = -4.75) である。もしこの明るさまでの LPV が全てタイプ I PNs に進化するとすると数が 3.5 倍になる。コアマスは 0.68 Mo まで下がる。そして、Mbol < -4.75 の AGB とタイプ I PNs の死亡率は 大体一致する。Mi - Mf 関係からはタイプ I PNs の母星は 2 Mo 以上の星となり、 Peimbert, Serrano 1980 が タイプ I に与えた母星質量下限の 2.4 Mo に 近い。 |
|
DA WD と non-DA WD 上に述べたように、いくつかの PNN はヘリウム燃焼と思われるが、この 10 年以上、AGB を離れる際に大部分の PNN は水素燃焼と信じられていた。ヘリ ウム燃焼 PNN は、非 DA 白色矮星を説明するために導入されたのである。 ヘリウムフラッシュ期に AGB を離れた PNN が 非-DA WD を作ると仮定された。 Iben 1984, 1987 はヘリウム燃焼 PNN が生まれる確率は 20 % とした。この 数字はフラッシュサイクルにおいてヘリウム燃焼期が占める割合である。Schonberner 1986 はこの数字を 25 % とした。DA と non-DA WD の質量分布はほぼ同一で ある。これは、DA と non-DA WD の誕生率に質量依存性が小さいことを意味 する。 高質量星の輻射駆動限界マスロス 27 進化計算の結果、低質量モデルの方がヘリウム燃焼 PNN 経路を生み出し 易いことが分かった。ただし、高質量星で以前に想定した輻射圧による外層 噴出を無視してだが。その理由はマスロス率とサイクル位相との相互作用で ある。 Vassiliadis, Wood (1993) 計算で、ヘリウムフラッシュ最後の２サイクルを見ると、 AGB マスロスは φ = [0.8, 1.0] の時、表面光度が極大の時にのみマスロス率は輻射圧駆 動限界値に達する。この高表面光度期＝水素燃焼期に外層はほぼ完全に吹き飛 ばされるので、われわれは星が AGB から離れるのは水素燃焼後半期であると 考える。このような星はその後の post-AGB 期にシェルフラッシュを起こすだ ろう。 |
更に高質量では、外層対流層が深くなるために、フラッシュ間隔時間に比べ ると、ヘリウムフラッシュからの回復時間（光度ディップからのかな？）が 短い。AGB 期最後のフラッシュで深い外層対流層が引き上がって行く時でも 回復時間は星質量星の場合に比べ短い。その結果、マスロスが高い水準にある 期間が長くなり、より広い範囲の位相 φ で AGB 離脱が起きる。Mi = 3.5, 5 Mo 進化経路 6 本のうち全てがヘリウム燃焼を起こさなかった。 銀河系バルジ PN からは低質量星がヘリウム燃焼 PNNs を生み出すように見 える。バルジ PN のかなりが Schonberner 1983 の 0.546 Mo PNN 経路より下 に位置する。この進化経路の速度はあまりに遅く、PNN が電離光を放射する頃 にはガスが散逸している。この現象は Mendez et al 1988, Gathier, Pottasch 1989, Pottasch, Acker 1989 などにより確認されている。この後略。 |
 図１３．Z=0.016 水素燃焼 PPN 進化経路に対する総エネルギー放出(LoMyr)/ (0.1logL/Lo)。 log(L/Lo) = 2.7 での垂直破線の右側の垂直スケールは 左側の１０倍である。線は質量が大きくなるに連れ濃くなる。 Renzini, Buzzoni 1986 が指摘したように、 AGB/PNN 種族は銀河放射の大 きな割合を占めている。またこの種族は楕円銀河の UV 超過の主成分である。 最近の研究はさらに新しい種族＝早期 post-AGB 天体の寄与が支配的と言う 結果を出している。 エネルギー放出の変化 Z = 0.016 の水素燃焼とヘリウム燃焼 PNNs 進化経路に対して、 0.1 log(L/Lo) 区間毎の総エネルギー放出量を図１３、１４に示す。これらの図は 表３，４から採った。図を見ると、水素燃焼 PNN で高光度一定期から log (L/Lo) = 2.7 へとどんなに急に落下するかが分かる。 |
 図１４．図１３と同じだが、Z = 0.016 ヘリウム燃焼 PNN 進化経路。 ヘリウム燃焼星の高光度期は長い PNN をヘリウム燃焼星に分類するのは PN 開始期でヘリウムを燃やしている かどうかで、そんな星でも post-AGB 期の大きな割合を水素燃焼で過ごす。 水素燃焼にくらべヘリウム燃焼の進化タイムスケールは長いので、ヘリウム 燃焼 PNN の方が総エネルギー放出の点では寄与大である。それは図１４で高 光度期 log(L/Lo) > 2.7 が図１３より明るいことに示されている。 低質量星の寄与大 類似プロットが低メタル星に対しても描ける。一般に低質量 PNN は進化タイム スケールが長いのでエネルギー放出の寄与が大きい。銀河のような星系全体では、 低質量 PNN は数が多いことと、個々の寄与が大きいことの双方から寄与が支配的 になる。 |
| 水素燃焼 17, ヘリウム燃焼 10 の PNN 進化経路を示した。前に比べ二つ、 改良点がある。１＝ 経験的マスロスを入れた AGB モデルに PNN 進化を接続 した。２＝最終風速の観測と輻射駆動マスロスモデルとを組み合わせて、 PN 領域でのマスロスを進化計算に組み入れた。 | 低質量 PNN は主にヘリウム燃焼であるが、それはぞれ以前の AGB 期のマス ロスの振る舞いによる。ヘリウム燃焼星は高質量でも現れるが、それは 輻射駆動マスロスの結果である。ヘリウム燃焼 PNN は低メタル量のマゼラン雲 ではより重要となる。 |