| 11 cm 連続波と再結合線強度の銀経分布ヒストグラムから、カリーナ腕とサジタリウス腕 は分離した構造であるという証拠が得られた。 | この推論は運動距離と無関係である。 |
|
電波と可視での渦状腕ピッチ角の違い これまで、太陽付近の渦状パターンには電波と可視光とで相違があった。 電波のパターンは一般に円形に近い平たい構造を示していた。一方、 可視光（ Bok (1959), Schmidt-Kaler 1968, Becker, Fenkart (1970), Courtes et al 1970 ）データはもっと立ったピッチ角を主張している。ただし、 Bok (1959) は可視光データに基づき、もっと閉じたピッチ角を主張した。 電波業界内での違い ２１ｃｍ観測では、同じではないが、同じようなデータを扱い違う結論が出ている。 その二つが 1969 年の バーゼル IAU シンポで対決した。 良く見ると、主に太陽近傍の解釈が影響している。 |
Kerr (1970a) 伝統的なピッチ角 7° の腕で解釈。シグナスからカリーナにかけて、 太陽を通って腕が伸びる。サジタリウス腕は太陽から銀河中心方向 2 kpc の 距離を通過し、連続して先に伸びて l = 305 で接点に達する。 Weaver (1970) 平均ピッチ角 12° の開いた渦で解釈。サジタリウス、カリーナ構造を合体 させ、シグナス腕と l = [305, 310] 構造はそこからの二本の枝と考える。 ギャップはリアル？ ここではサジタリウスーカリーナギャップに注意を集中する。 |
|
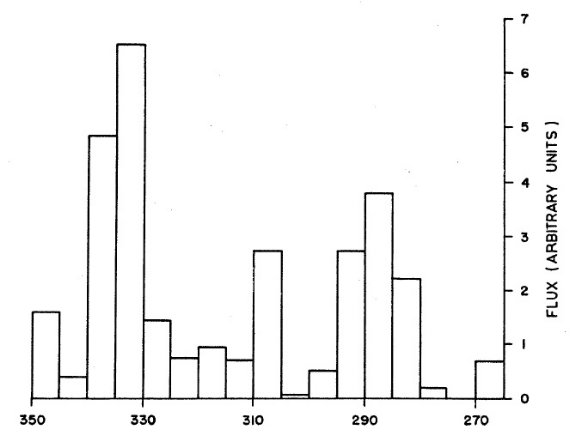
図１＝パークス 11 cm 波サーベイ 図１はパークス 11 cm 波サーベイの結果である。l = [292, 304] でフラッ クスが低い。l = 304 には腕の接線方向で期待される段差がある。第２段差は l = 326 にある。これはノルマ腕に帰される。公表されたデータはまだ カリーナ構造の全てに亘っていない。しかし、 l = [288, 292] の盛り上がり はおそらくカリーナ腕に関連するだろう。ちなみにこのような段差は Mills 1959 が最初に発見した。 ギャップの距離 このように、 11 cm サーベイは l = [292, 304] にギャップの存在を 明らかにしている。 Thomas, Day 1969 の等高線マップを見ると、放射 が狭い帯に集中していて、その中心線が銀河赤道の下側にある。 これは放射物質が遠方にある時に期待される特徴で、太陽から数 kpc までは熱放射物質はほぼないと言える。 |
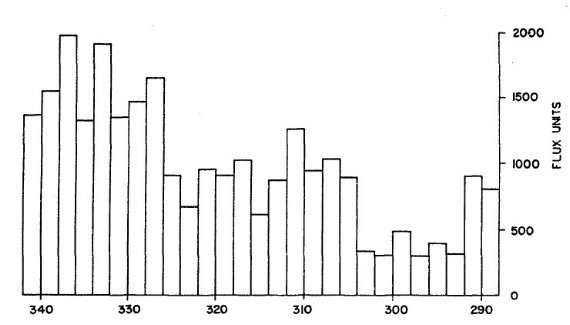
 図１．11 連続波 b = [-2, 2] 積分強度の銀経による変化。 |
| 類似情報が H109α データ (Wilson 1969) からも得られる。 しかし、データは幾つかの点源観測をつないだものとなる。 図２はその点源データから推定したフラックス分布である。この図にも カリーナ、サジタリウス、ノルマ腕の特徴が現れている。 |
 図２．H109α 推定フラックスの銀経による変化。 |
|
ギャップは本物 上記二つの結果は l = [295, 305] 区間には電離ガスが殆ど存在しないこと を示す。また、図からはサジタリウス腕が l = 305 で接点に達するまで 連続して伸びていることを支持している。もし、カリーナ腕と サジタリウス腕の間につながりがあるとしても、我々はそれは渦状腕の 主要構造ではないと考える。 |
方法の利点 Mezger は今回のような積分放射による研究は、視線方向に近傍 天体が偶々重なった時の影響が大きく、渦状腕の位置を決めるには 不適当と議論した。しかし、今回のデータは個々の近傍天体 が影響できるスケールでない。この方法の優れている点は 速度情報を使っていないことである。 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|