Short- and Intermediate-Period Oxygen-Rich Miras

　アブストラクト　

　１．イントロダクション　

　２．サンプル　

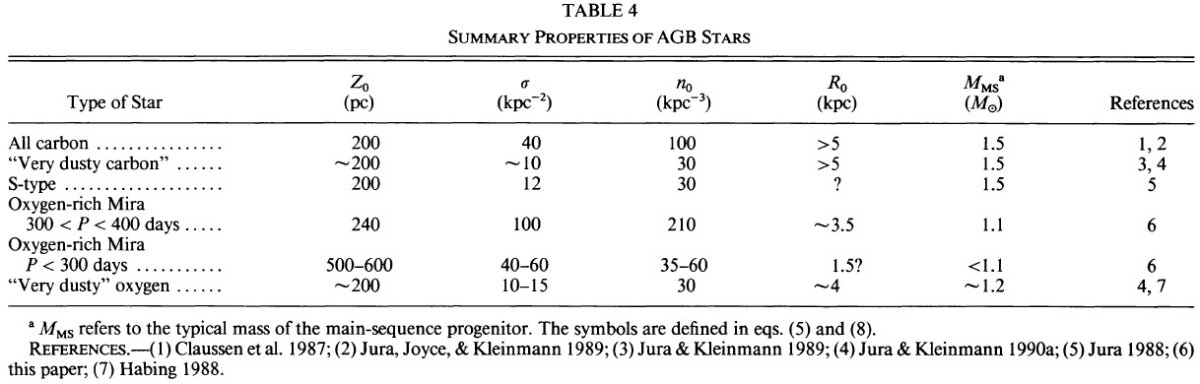
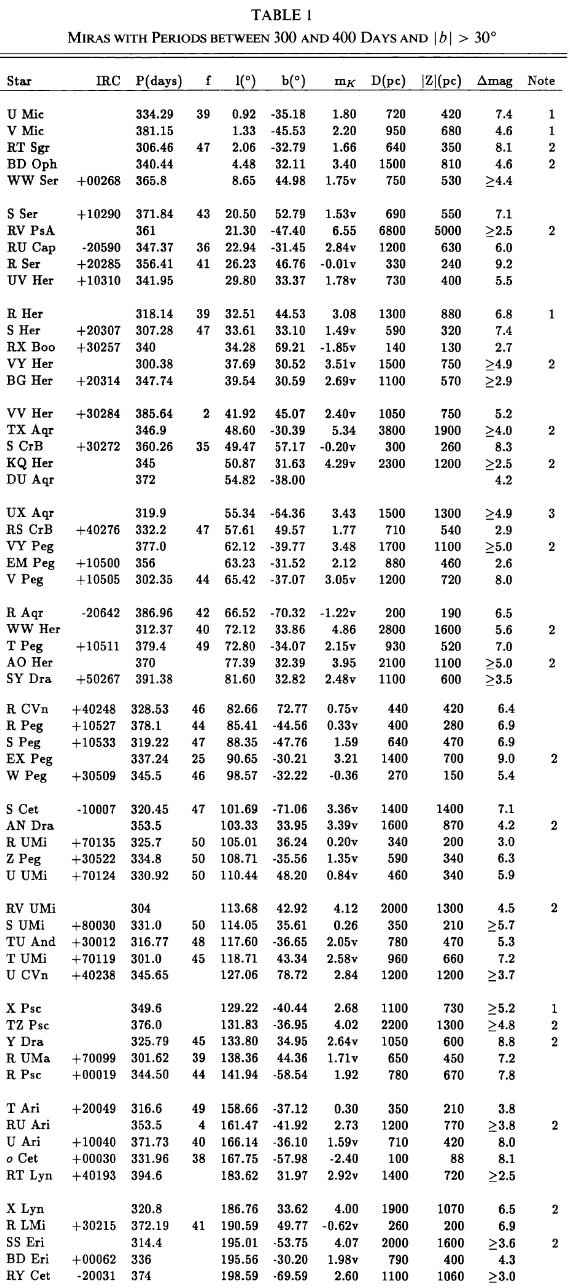
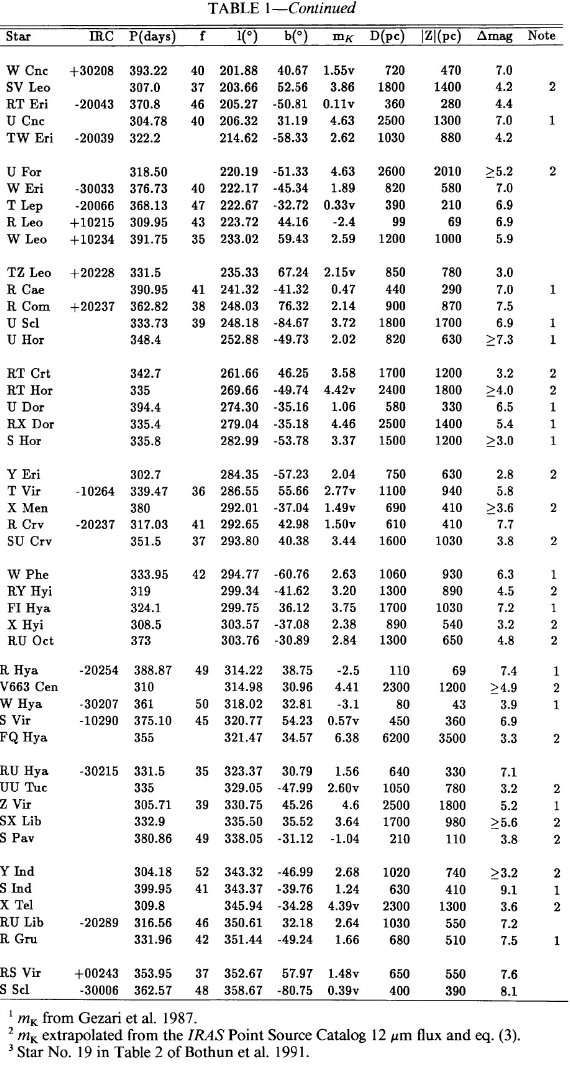
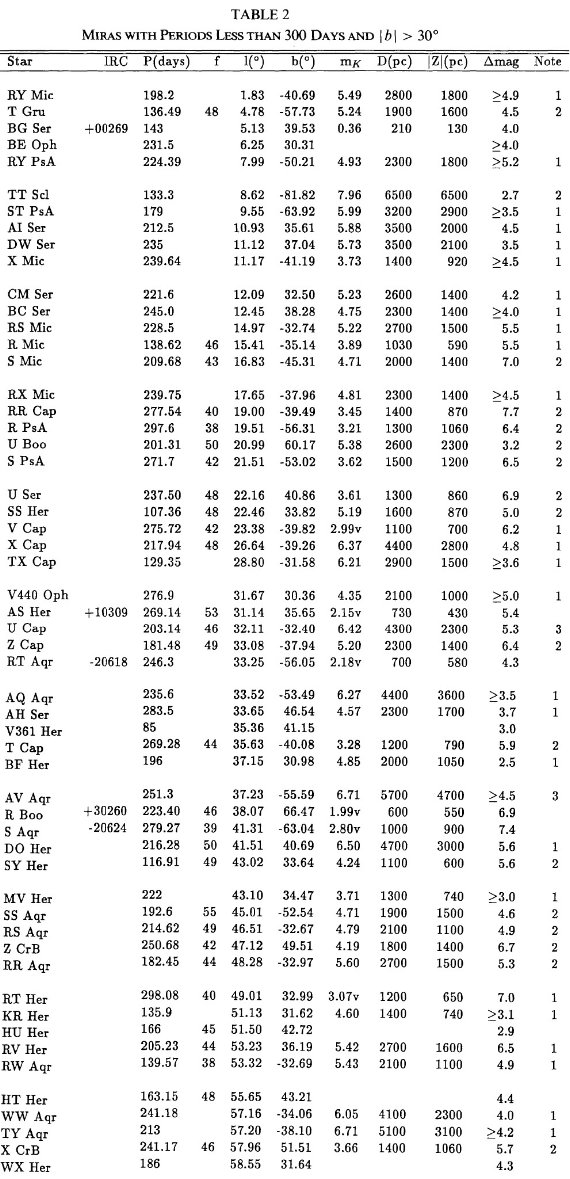
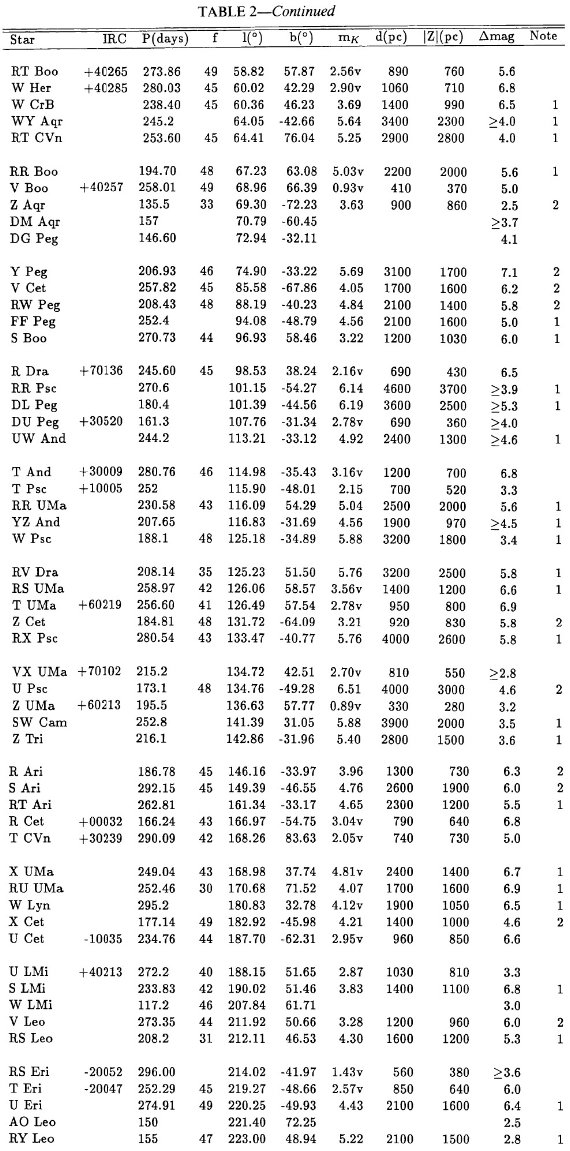
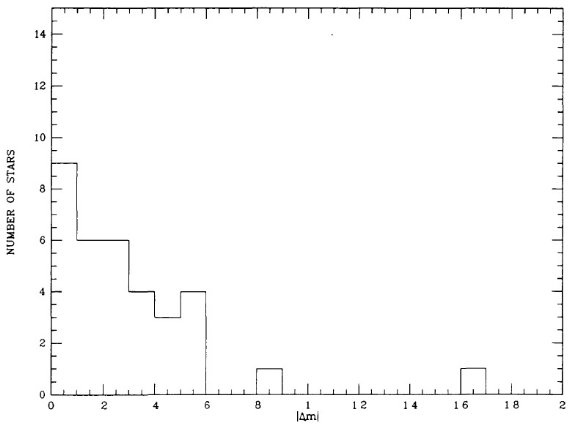
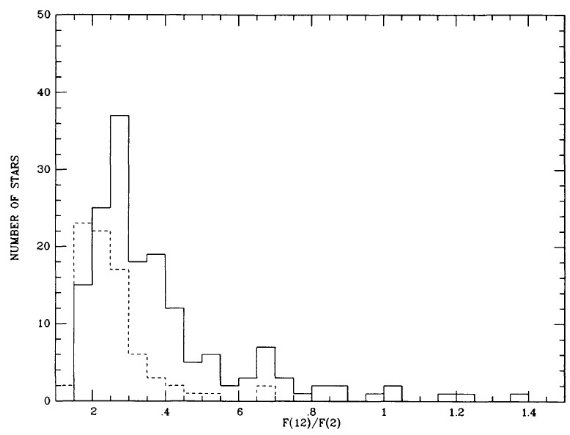
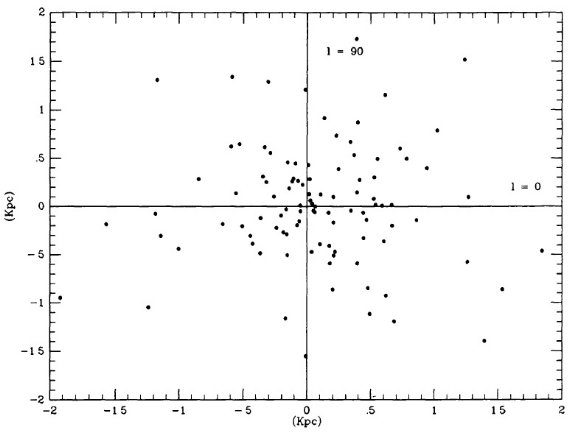
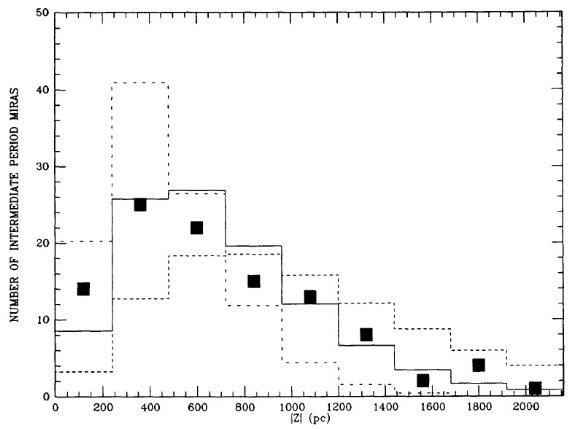
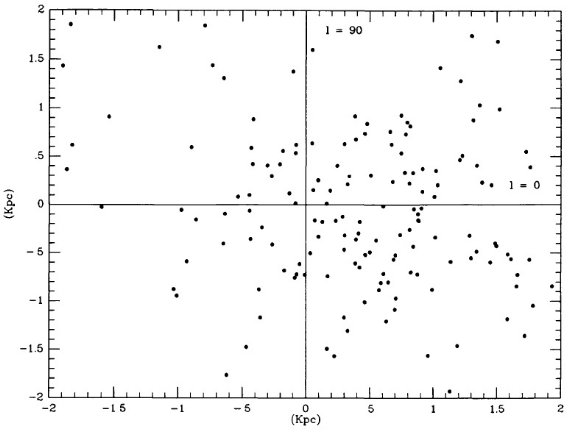
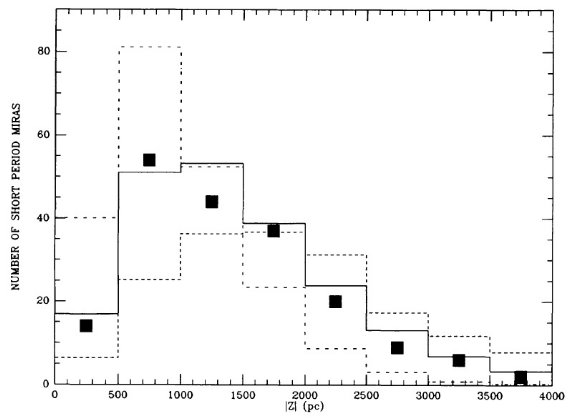
規準　 　|b| > 30° だと、（１）Av < 1 mag, （２）グールドベルトの 影響がない、（３）分子雲もない、（４）可視探査がほぼ完全、という利点がある。 我々は、vis または blue バンドで Δm ≥ 2.5 mag, P ≥ 80 d をミラとした。GCVS では時々それらの要件を満たしてもセミレギュラーとして いるが、ここではすべてミラとする。特に炭素星と記していない星は酸素超過と 仮定した。 　リスト　 　表１には P = [300, 400] d の 107 星を、表２には P ≤ 300 d の 211 星を載せた。90 % 以上が GCVS でミラとされ、残りはセミレギュラーと分類 されていた。表の f = 可視変光曲線の非対称性パラメタ―は重要である。 Whitelock et al 1991b に従い、XY Tau は表２から落とした。 図１には振幅のヒストグラムを示す。 　周期・光度関係　 　Feast et al 1989 は LMC の周期・光度関係を次のように表した： 　　　MK = -3.47 log⟨P⟩ + 1.01　　(1) Wood 1990 は銀河系星に対し、脈動理論の外挿から、0.25 暗くした： 　　　MK = -3.47 log⟨P⟩ + 1.26　　(2) この論文では (2) の方を採用する。また、星間減光は無視する。

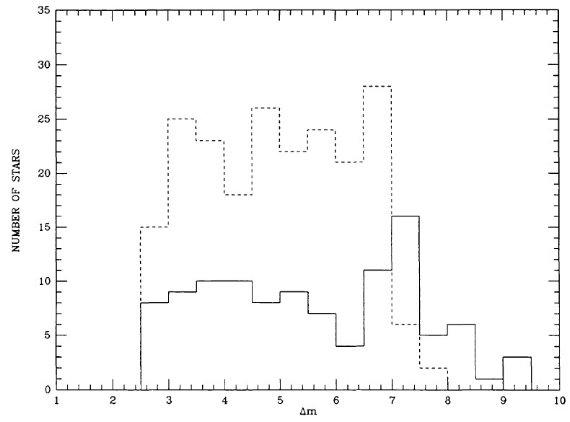
図１．振幅ヒストグラム。破線：P < 300d. 実線：P = [300, 400] d.

　表１：P = [300, 400] d, |b| ≥ 30° ミラ　

　表１：P ≤ 300 d, |b| ≥ 30° ミラ　

図２．|mK(TMSS) - mK(SAAO)| ヒストグラム。 mK(TMSS)= Neugebauer,Leighton 1969. mK(SAAO)= Catchpole et al 1979. 　 　K 等級　 　K 等級の多くは TMSS = Two Micron Sky Survey (Neugebauer,Leighton 1969) から採った。TMSS より暗いものは、文献から集めた。図２には TMSS と Catchpole et al 1979 との差をヒストグラムとした。大部分は 0.5 mag 以内 に収まるが、 R Aqr は大きく、注意が要る。

図３．TMSS 星に対する F(12)/F(2.2) のヒストグラム。破線＝ P<300dミラ。 実線＝P=[300, 400]d ミラ。 　 　　 　K 等級が見つからなかったものは, K 等級が見つからなかったものは IRAS F12 から K 等級を決めた。図３には F(12)/F(2.2) のヒストグラムを示す。 分布の中間値を取り、P = [300, 400] d ミラに対しては、 F(12)/F(2.2) = 0.31 を仮定し、P < 300 d ミラには F(12)/F(2.2) = 0.25 を仮定した。

　３．中間周期ミラ　

　３．１．中間周期ミラの空間分布　

図４．表１の中間周期ミラ 107 個の銀河面上の投影分布 　密度分布関数　 　表１の中間周期ミラ 107 個の位置を次の式でフィットした。 　　　n = n0 exp(-|Z|/Zo) exp[-(R-R*)/Ro]　　　　(5) (R* = 太陽銀河中心距離の値が見 つからない。 ) 図４に表１の星位置の銀河面への投影を示す。図から、銀河中心側の星 61 個 は銀河反中心側の星 44 個よりやや多いことが判る。 　スケール長 Ro　 　銀河系動径に沿ったスケール長は、l = [330, 30] の 20 星と l = 150, 210] の 14 星から決めた。銀河面に投影した二つのグループの星の(重心？)距離 の中間値は 700 pc である。我々の探査帯で高銀緯（高銀河面距離かも知れない） の星の表面密度は、銀河中心距離 R が 700pc x 2 = 1.4 kpc 変わる間にファ クター 1.5 変化がある。これから我々は Ro = 3.5 kpc を導いた。 (確かに、exp(1.4/3.5)=1.49 だが、 "high latitude" での密度比をどうやって導いたか、肝心のデータがない。 この論文の眼目の一つなのに。図４を虚心に見ると、太陽円± 0.3 kpc 当たりでは、外側の方が多いぞ！）

図５．表１の中間周期ミラ 107 個の銀河面からの高度ヒストグラム。 点線＝式(5), Zo=160 pc. 実線＝式(5), Zo=240 pc. 破線＝式(5), Zo=360 pc. 　Zo を決める。　 　Ro がこのように大きいので、Zo を決める時 R による n の変化を気にする 必要はない。式 (5) から、我々の双円錐領域内の星数 N* が次の式で表される。 　　　N* = 4πn0Zo3cot2bcr 　　　(6) ここに、bcr = 我々の円錐の最低銀緯である。式 (6) から、Zo の 評価をサンプル星の高度中間値 Zmed で以下のように評価できる ことが判る。 　　　Zmed = 2.7 Z0 表１の 107 星に対し、Zmed = 650 pc である。反中心方向で 700 pc, 中心方向で 600 pc なので、平均が 650 pc であった。それから導かれる Zo = 240 pc である。 ( 650 pc は円錐形状に対する価で ないといけないが、明記されていない。Ro でもそうだが、直接フィットしようと しないのは裏に理由があるのか？なんか怪しい。） 　図５＝銀河面高度分布　 　図５にはサンプル星の銀河面高度分布を、式 (5) と較べた。 Zo = 160, 240, 360 pc の間では Zo = 240 pc が最適であることが良く分かる。この値は、 Habing 1988 が 赤い IRAS 天体の薄い円盤に対して与えた 200 - 250 pc, Jura, Kleinmann 1989 が非常に塵の厚い AGB 星から導いた 200 pc と合っている。

　３．２．質量放出率　

CO 観測から決める　 　van der Veen, Rugers 1989 は質量放出率の決定にかなりの誤差が伴うことを 注意した。我々は、 CO 観測からと IRAS FIR 観測からの質量放出率の推定が かなり良く一致することに気が付く。表３には近傍の中間周期ミラに対して Bujarrabal, Gomez-Gonzalezm, Palnesas 1989 が行った CO 観測の結果を 示す。彼らの使った距離Ｄを我々の表１の値に置き換えた dM/dt が載っている ことに注意せよ。 　IRAS から決める　 　Jura 1987 は以下のダスト放出率を提案した。この式は Sopka et al 1985 の解析が元になっている。 　dM/dt = 1.1 10-8vdustDkpc2 L4-1/2Fν(60)λ10 1/2 ここに、vdust は　km/s 単位、L4 = L/104Lo, Fν(60)は Jy 単位、λ10 = 赤外スペクトルの 平均波長、である。Wood 1990 から L4 = 0.5 とし、中周期ミラに 対して λ10 = 0.15 とした。距離は表１から採った。 　vdust 　 　放出率が大きく、dM/dt が L/(cv∞) に近い 時には vdust = v∞ = ガス流出 速度となる。dM/dt << L/(cv∞) ならば、ダストは ガスに対して vst の相対速度を持つ。その時、 Kwan, Linkke 1982 に依れば、 　　　vst = v∞Q1/2[(L/cv&infin: dM/dt)]1/2

表３．近傍の中間周期ミラの質量放出率 で、vdust = v∞ + vst である。 L4 = 0.5, v∞ = 5 km/s に対して、 L/(cv∞) = 2 10-5 Mo -1 であり、 ミラ型星に対し、vdust = 2 v∞ とすると、 マスロス率は (1-2) 10-7 Mo -1 となる。

　４．短周期ミラ　

　４．１．空間分布　

図６．表２の短周期ミラの銀河面上への投影。図６には短周期ミラの銀河面上 への投影を示す。 　小さなスケール長　 　表２には 211 短周期ミラが載っている。銀河中心方向への集中が明らかで ある。中心方向 l = [330,30] には 61 星があり、その平均距離は 1500 pc である。反中心方向 l = [150, 210] には 11 星で平均距離 800 pc である。 つまり、、銀河系中心距離が 2300 pc 変わる間に表面密度がファクター５ 変わったと考えられる。これから導かれるスケール長は 1.5 kpc である。 この値は、Habing 1988 が IRAS の薄い円盤種族に与えた 4500 pc, 厚い 円盤種族に与えた 6500 pc に較べると著しく小さい。ただし、 Habing の 結果は内部銀河系の円盤に対するものであり、一方太陽近傍では太陽円 の外側 1 kpc にカットオフが存在する。 　太陽円 1 kpc 外側のカットオフ　 　Habing が見つけた薄い円盤種族の大質量放出星に存在するカットオフは彼の カラー選択が炭素星を除いていたことと、炭素星とM-型星の比率の勾配が大きい Jura (1990) ことの二つが原因である。現在のところ、短周期ミラの銀河中心距離に伴う急な 減少がこれらの星の性質が急に変化するためと言う証拠はない。 　スケール高　 　では、式 (5) に基づいてスケール高を決めよう。もし、距離が未定の星の 距離を全て中間値より遠いと仮定すると、中間高度 = 1400 pc である。もし 距離未定の星がランダムに分布していると仮定すると、短周期ミラの銀河面高度 の中間値は 1300 pc である。真の中間高度 = 1350 pc とすると式７から、 Zo = 500 pc である。P = [100, 200] d と [200, 300] d の間に Zo の差が 認められなかった。図７では、異なった値の Zo を使ったモデルを比較した。 観測と合うのが Zo = 500 pc であることが判った。周期-K 関係に式 2 の代わ りに式 1 を使った時の Zo は 600 pc であった。付録Ａでは、距離 2 kpc 以 内では我々の短周期ミラサンプルは 75 % 完全であるという議論を行う。この 距離は Zo = 500 pc より十分に大きく、我々の求めた Zo が安全であることを 保証する。

図７．短周期ミラの銀河面からの高度ヒストグラム。実線＝スケール高 Zo 500 pc のモデル分布。破線＝ Zo 750 pc, 一点鎖線＝ Zo 330 pc. 　Zo は安定　 　議論を |b| > 60° に限って、銀河中心距離による密度勾配の影響を 被らないようにしたら、再び中間高度 1350 pc を得る。同様に、銀河中心方向 と反中心方向に星を分けても両者同じ値を得る。このように Zo は安定している。 　局所密度、局所コラム密度　 　局所密度、局所コラム密度を得るには、銀河面投影距離が長い星は使えない。 そこで、 |b| > 45° の星のみを使用した。その結果、 n0 = 60 kpc-3, σ0 = 60 kpc-2 である。 もし、Zo = 600 pc を採用すると、n0 = 35 kpc-3, σ0 = 40 kpc-2 となる。この値は Habing (1988) が厚い円盤の大マスロス星に対して求めた 2.5 kpc-2 より大分大きい。 　　 　短周期ミラの空間分布は楕円体分布でなく、円盤分布である。なぜなら、今の所 スケール高が銀河中心距離により変わる証拠がないからである。

　４．２．マスロスとメタル量　

　５．議論　

　６．結論