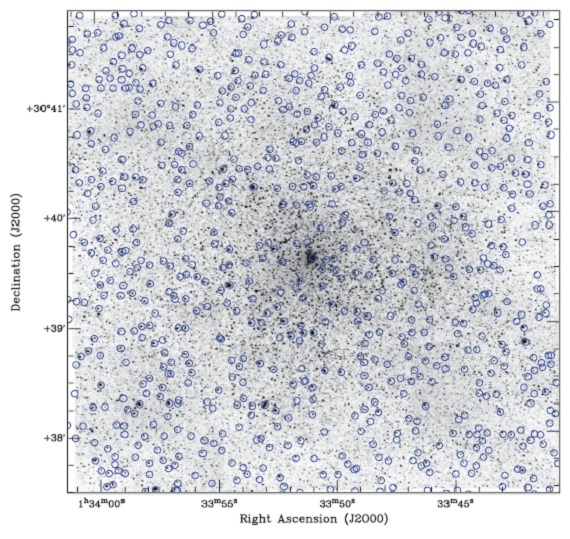
図1.M 33 中心1キロパーセク四方の Ks 画像. 丸=McQuinn07 の MIR 天体。
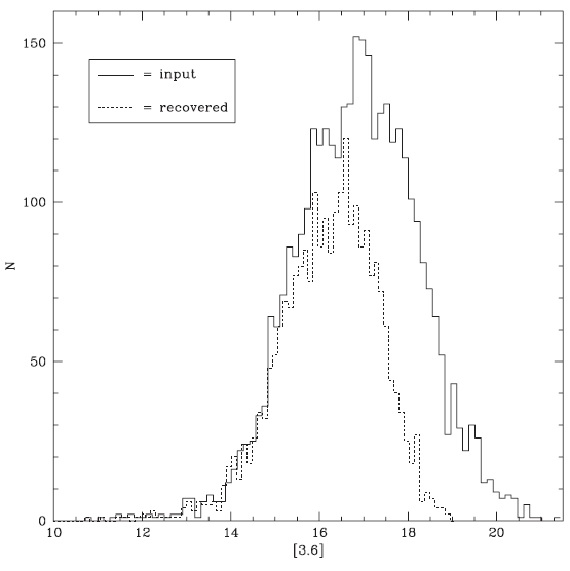
図2.実線=入力 Ks 分布。点線=回復等級分布。
| この第3論文では、脈動 AGBs によるマスロス率を測る。その為、UKIRT NIR 観測に,Spitzer MIR 観測を組み合わせる。低質量星はその初期質量の 大部分を星風により失う。しかし、スーパー AGBs や RSGs でさえも質量の 40 % を星風によって失う。 | ダスト還流の 3/4 以上は酸素系である。マス還流率の 2 D マップを作った。 それは動径に沿った低下を示すが、大質量星の集団があるところでは局所的 盛り上がりを示す。マスロス率は, 中心キロパーセク領域で 0.006 Mo yr-1 kpc-2 である。ここには、爆発的、例えば超新星、 のような現象も考慮した。これを現在の星形成率 0.03 Mo yr-1 kpc-2 と比べると、現在の星形成を維持するには、外側円盤からの ガス流入か、銀河間ガスの降着が必要である。 |
 図1.M 33 中心1キロパーセク四方の Ks 画像. 丸=McQuinn07 の MIR 天体。 |
 図2.実線=入力 Ks 分布。点線=回復等級分布。 |
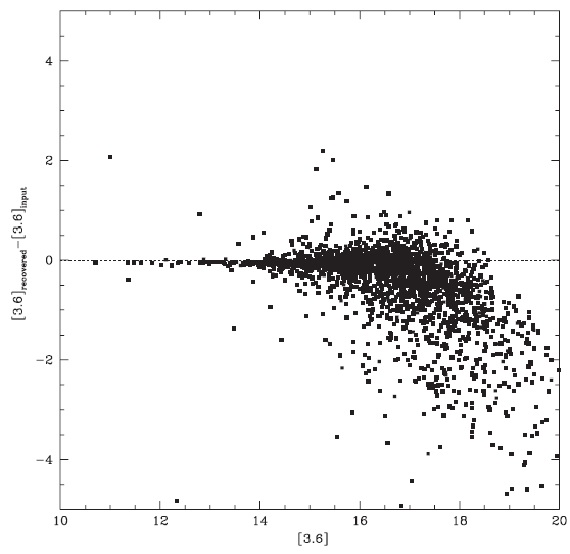 図3.入力等級と回復等級の差と入力等級の関係、 |
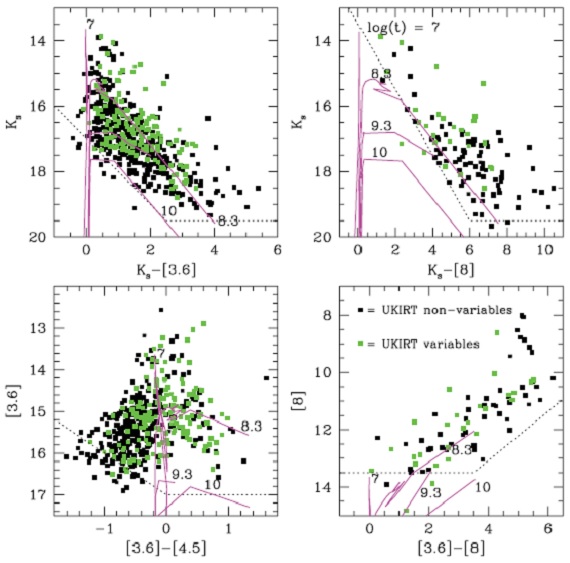 図4.NIR/MIR CMDs。点線=近似的検出限界。赤線=Marigo08 等時線 (log t = 7 -10) |
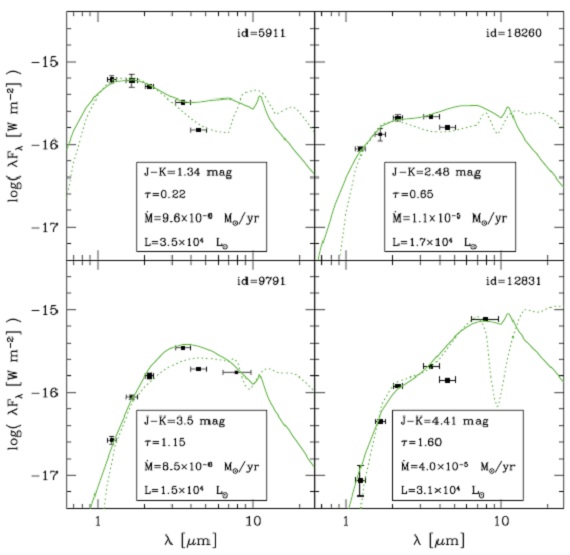 図5.炭素星サンプルの SED. jissenn = DUSTY ベストフィット。 点線=比較のためのシリケイトモデル。 |
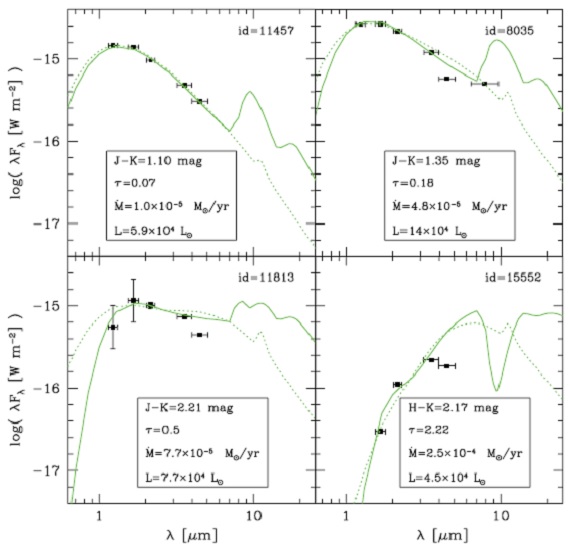 図6.M-星サンプルの SED とDUSTY フィット。 |
|
SED フィット J H Ks のうち少なくとも二つのデータがある UKIRT 変光星で、 IRAC 3.6, 4.5, 8 μm データの内二つが揃っている星を DUSTY によりモデル化した。 測光データが少ないので、モデルの星温度= 3600 K, ダスト内径温度= 900 K に固定した。論文II の星形成史に基づき、M = [1.5, 4] Mo 星には 非晶質炭素と少量の SiC ダストを、その他の質量には天文シリケイトを適用 した。こうして、58炭素星と、35M-型星の光学的深さ τ, 光度 L, マスロス率 dM/dt を求めた. 表7。 フィット例を図5と図6に示す。 モデルとした。 |
モデルフィットの検討 星のマスロスと光度は数桁の範囲に渡り、フィットで使用した仮定の影響は 比較的小さい。4.5 μm の測定はモデルより有意に低い場合がしばしばある。 モデルには入っていない CO 吸収帯が原因と思われる。 |
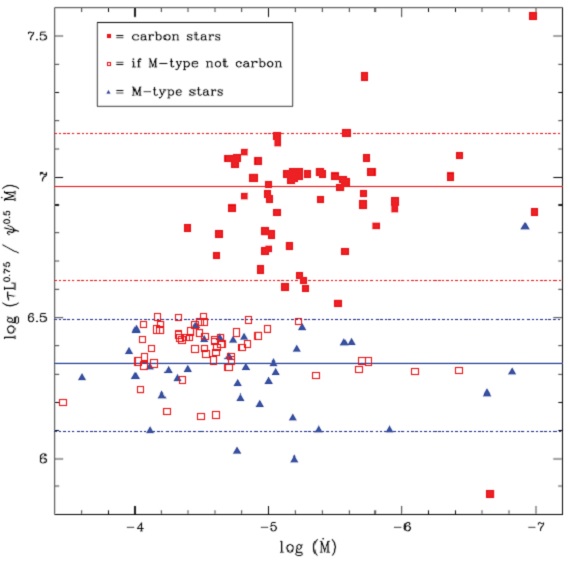 図7. Ivezic, Elitzur (1997) のマスロス定数と dM/dt の関係。 抜け赤四角= 炭素星を仮に O-リッチと扱った場合。 青三角= O-リッチ AGBs. 赤四角=炭素星 抜け赤四角=炭素星を仮に O-リッチと扱った場合。 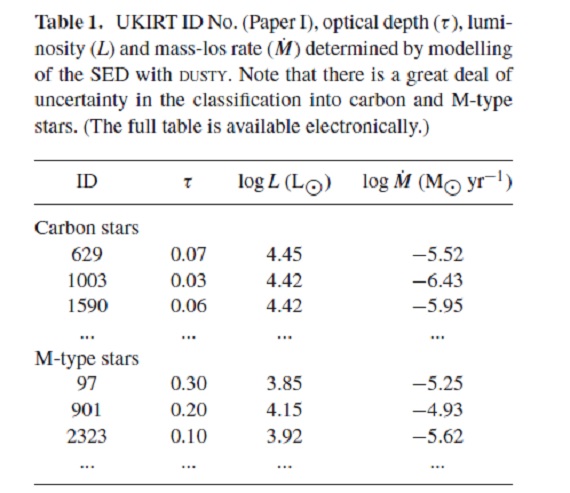 表1.DUSTY モデルの結果のサンプル例。 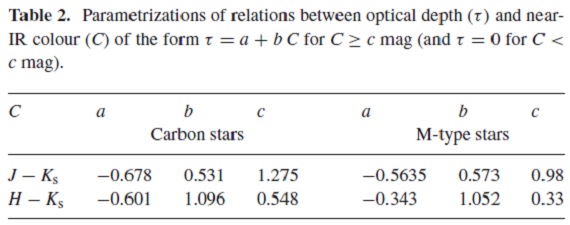 表2.光学的深さ τ と NIR カラー C の関係式 τ = a + b C の係数。ただし、 C ≥ c の場合である。 |
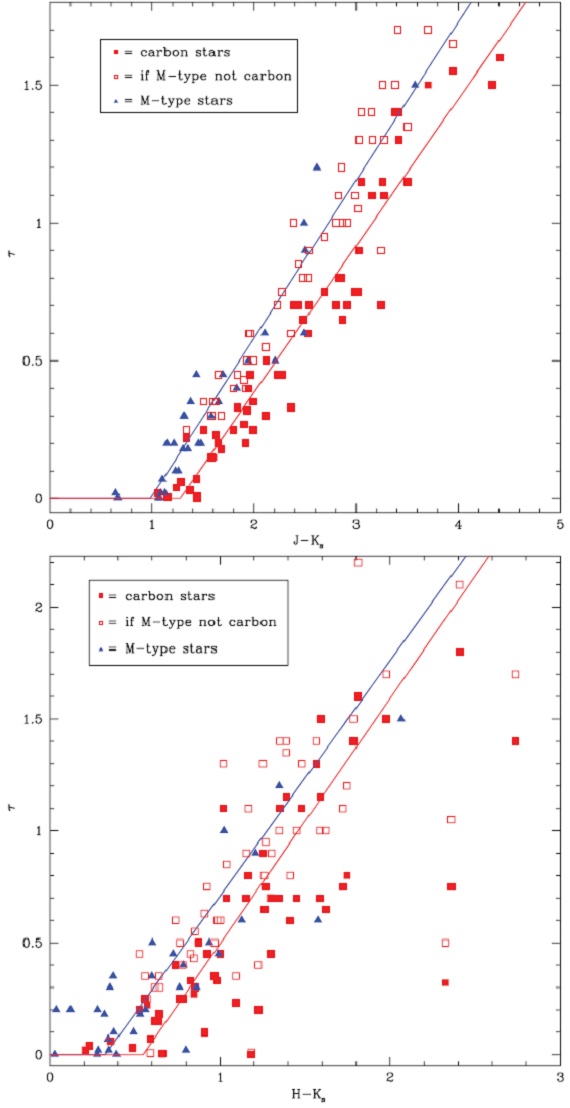 図8.光学的深さ τ と NIR カラー C の関係。抜け赤四角= 炭素星を仮に O-リッチと扱った場合。赤線=炭素星のフィット直線。 青線= M-星のフィット直線。 (τ は 何か書いていない。) スケーリング Ivezic, Elitzur (1997) は星風モデルで、 (τ L3/4)/[ψ1/2 (dM/dt)] が一定値となることを見出した。実際それは図7に示すように 0.2 dex のばら つきで一定である。 (論文を覗いたがどれがそれに当たるか 不明。Vwind の L 依存も組み込んでいるらしい。τ は τV の事かと思うが記述ナシ。L をどう出したのかも書いていない。兎に角 無茶苦茶) |
3.1.ダスト形成とマスロス率図10: マスロス率と光度 L の関係図10に示すように、マスロス率は光度 L と幾分かの相関を示す。 1).最大マスロス率は大質量星で達成される。MW の炭素星が到達 する最高値は 数 10-5 Mo/yr Whitelock06 である。 マゼラン雲では 10-5 Mo/yr で、これは M 33 での炭素星 最高値にほぼ等しい。 太陽近傍では、 M-AGBs が似たような値 数 10-5 Mo/yr Juta, Kleinmann (1989) に達している。MW の M-型超巨星は dM/dt = 10-7 - 10 -4 Mo/yr Juta, Kleinmann (1990) で M 33 とこれも似る。 マスロスの進化効果 ある光度に対するマスロス率の広がりは恒星進化を反映しているらしい (van Loon 1999, 2005). L < 4 の暗い炭素星はおそらく AGB 先端に達し ていない。というのは、同じ光度でもっとマスロス率が高い M-AGBs が存在 するからである。これらの M-AGB は比較される炭素星より進化の進んだ星で あろう。ただし、これらの炭素星が再び M-AGBs に回帰するわけではなく ( Marigo et al. (2008), ) さらに高い光度へと大きなマスロス率へと進化して行く途中なのであろう。 (マスロス変光星は必ずしも AGB 先端にないということか。すると光度から質量が出せなくなるが、 この論文ではどう扱っているのか? ) それとも熱パルス効果? もしくは、低光度で低マスロスの炭素星は間パルス期の落ち込みにあり、 非常に明るく高マスロスの星は熱パルス直後にあるのかも知れない。 シリケイトだとマスロスが上がる。 炭素星と分類した星をシリケイトダストでフィットすると、吸収率が低下する ためそれを補うためマスロス率が増加する。 図10の #12831 (J-Ks = 4.4, AKs=0.63)はそのよい例で log(dM/dt) = -3.5 と、9倍にもなる。 ("than if fitted with silicates" とある のは逆?それと同じ L の赤四角がないのは BC も変わるから?) RSGs マスロス率は Teff に強く依存し、RSGs の Teff は AGBs ほど低くならない ため、 RSGs マスロスは AGBs より低めである。 Spitzer の無い星 図11には Spitzer 測光がない星や非変光星も含まれている。 (と書きつつ、 Spitzer 画面上で 非常に明るいのにカタログに載っていない星に話が移って行き、 SED フィットしない多数の小さい緑点のマスロスをどう決めたかは知らん顔。) |
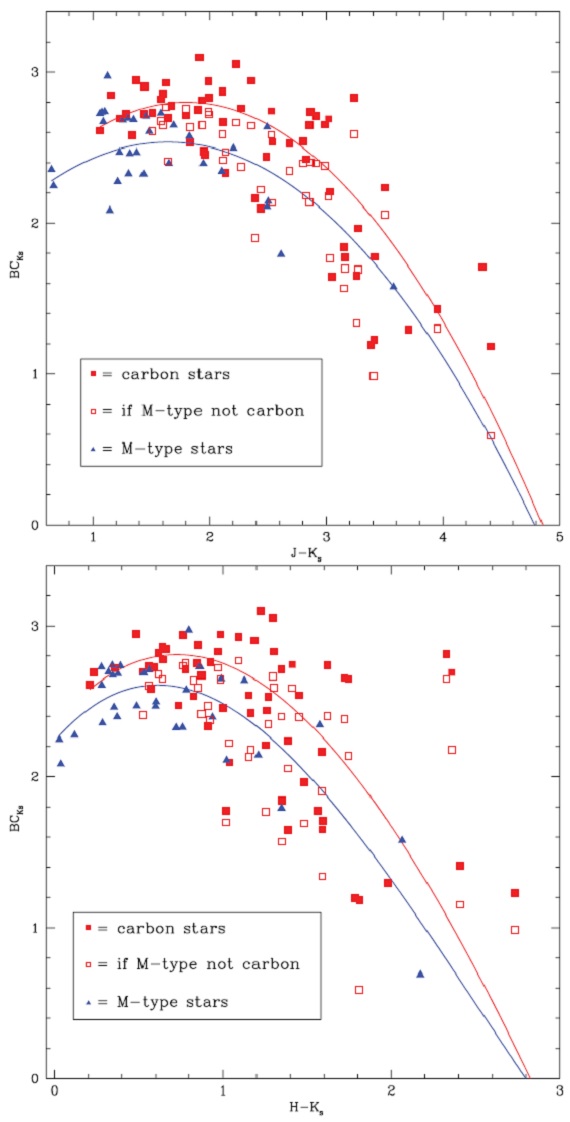 図9.BCKs と NIR カラーの関係。抜け赤四角= 炭素星を仮に O-リッチと扱った場合。赤線=炭素星のフィット線。 青線= M-星のフィット線。 |
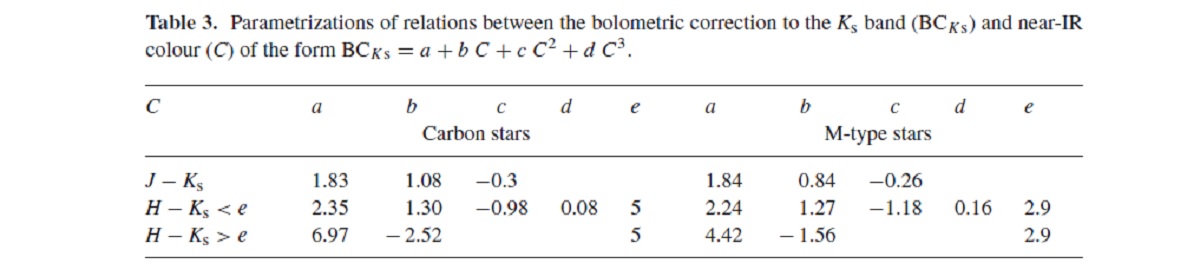
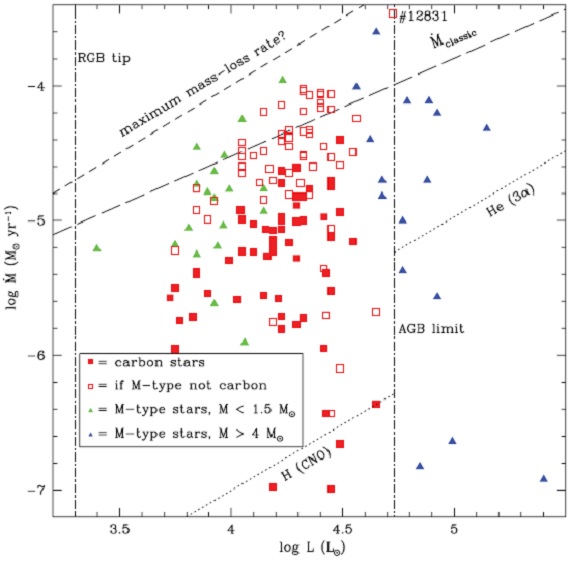 図10.DUSTY から決めたマスロスと光度の関係。緑三角=低質量 O-リッチAGBs. 赤四角=中間質量 C-リッチAGBs. 青三角= RSGs. 抜け赤四角=炭素星を仮に O-リッチと扱った場合。 斜め点線=殻燃焼によるコアマスの増加率。 K バンド振幅 図12に示すようにマスロス率は K バンド振幅と共に増加する。 カラー 赤外カラーがマスロス率に相関することはよく知られている。しかし、カラ ーをマスロス率に変換する際には、光度、ダストの性質についての注意が必要である。 図13にそれを示す。 (「シリケイトを仮定して」という やり方がどういう論理で編み出されたのかさっぱり理解できない。何だろ?) 炭素星は簡単に赤くなるが、そのマスロス率はそれより青い M-型星と同じである。同様に、同じ性質のダストでも、暗い星は明るい星と較べより 低いマスロス率で赤くなる。炭素星の光度は低質量星と高質量星の中間にある。そして 実際、炭素星にシリケイトを仮定してマスロスを求めると中間に来る。 (「シリケイトを仮定して」という やり方がどういう論理で編み出されたのかさっぱり理解できない。何だろ?) |
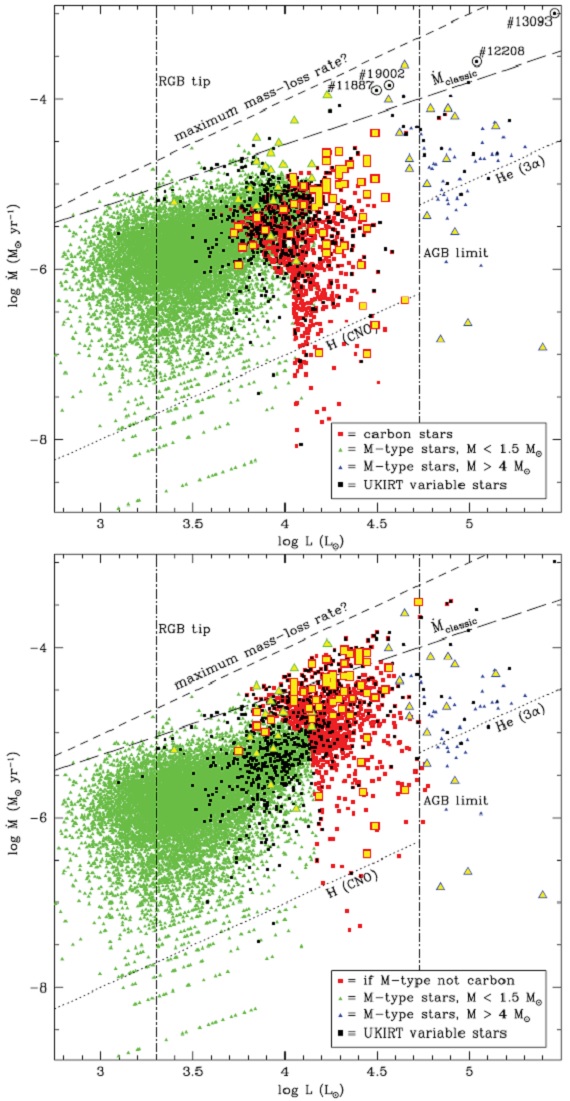 図11.マスロスと光度の関係。緑三角=低質量 O-リッチAGBs. 赤四角=中間質量 AGBs. 青三角= RSGs. |
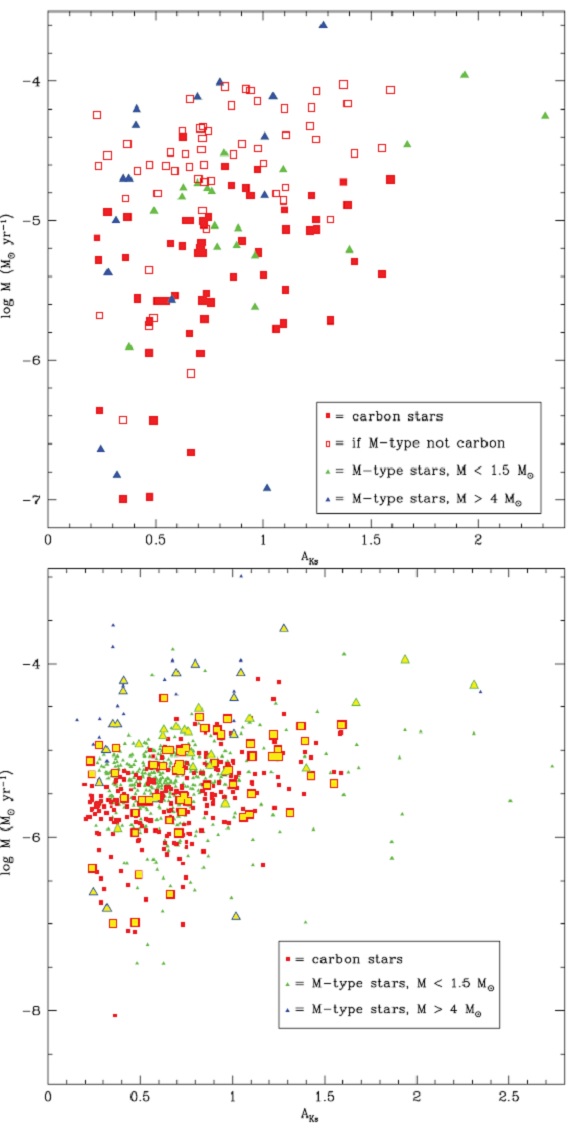 図12.マスロスと Ks 等級の関係。 |
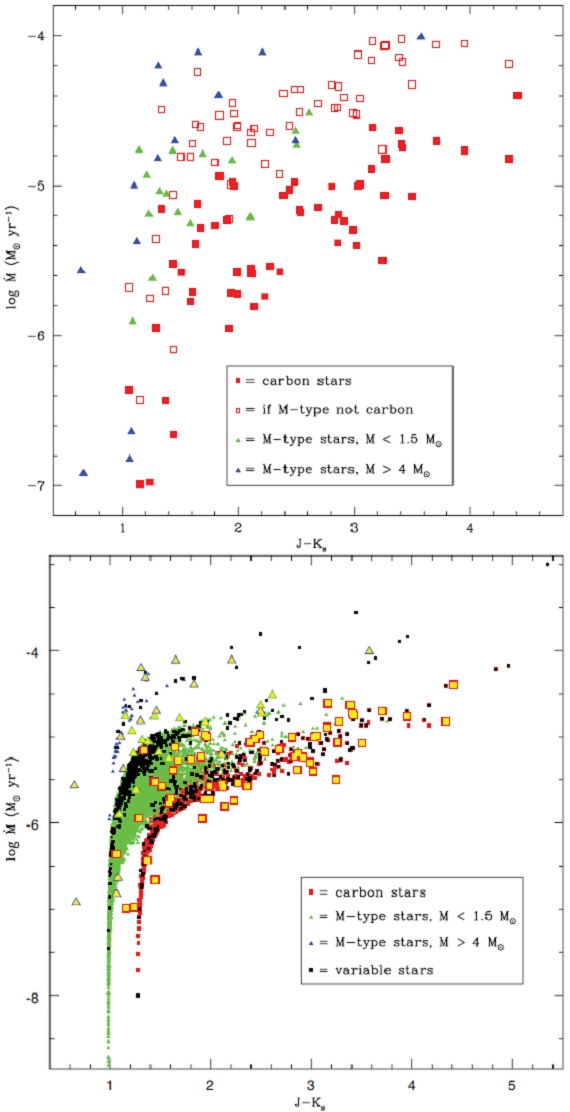 図13.マスロスと J-Ks カラーの関係。 |
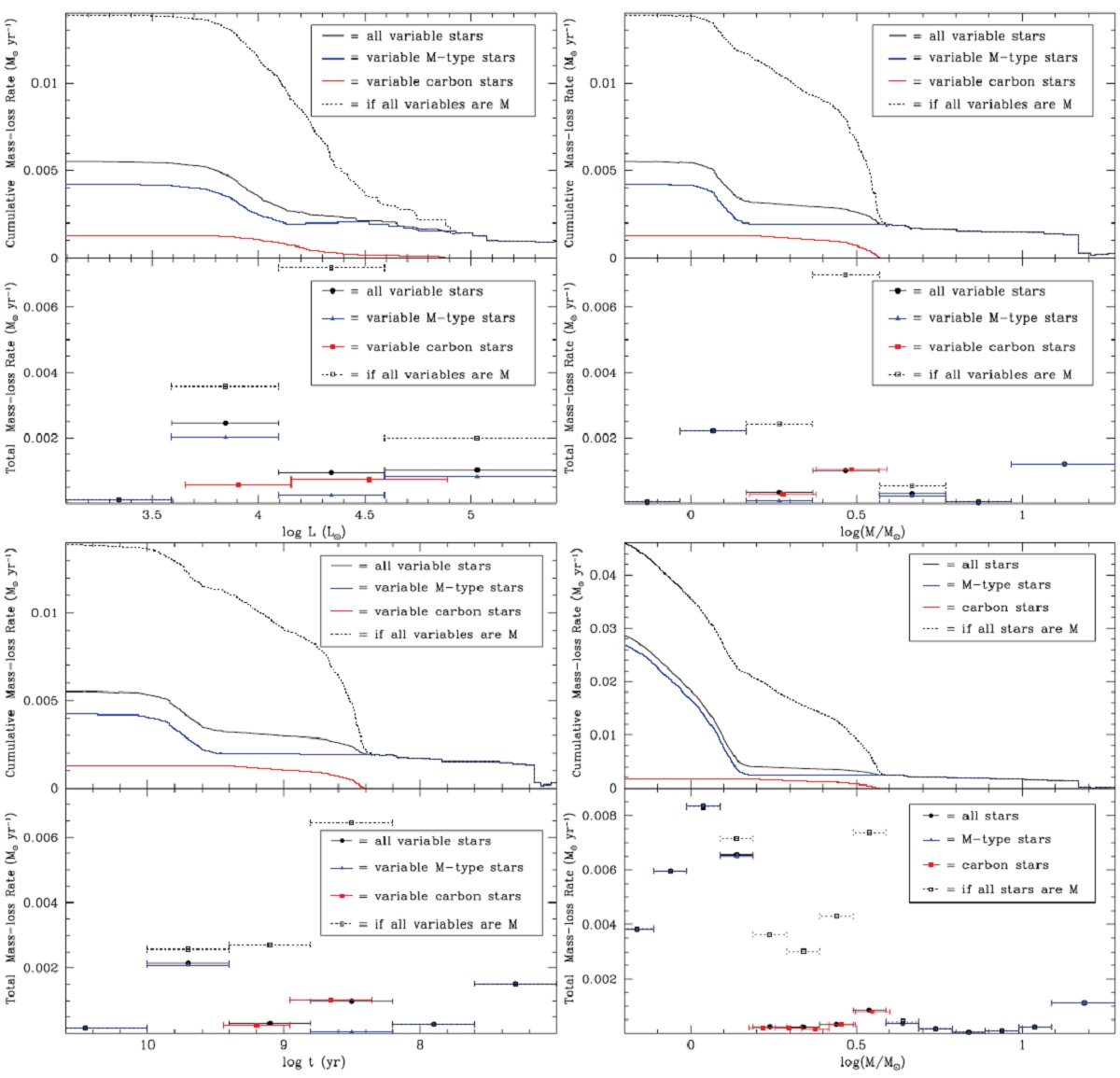
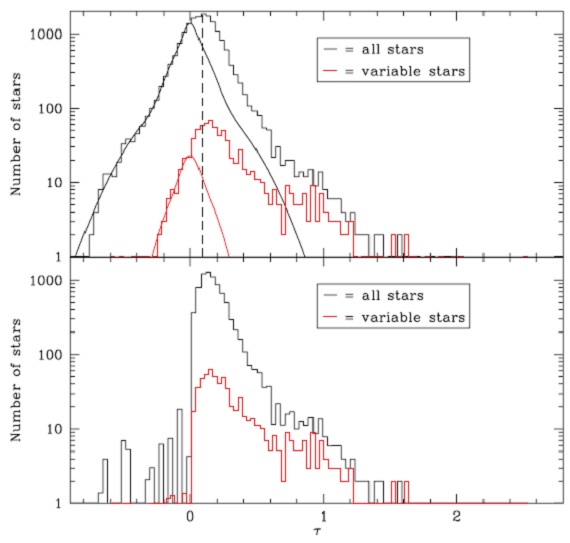 図14.上:τ 分布。下:τ 負の部分を削った、分布。 低質量星の τ 系全体のマスロスは、小さい系でのストカスティックな大質量星の出現、多数の 極低マスロス星の扱いなどの注意が要る。多くの赤色巨星が穏やかなマスロスを しているが、それらの小さな赤化は星間赤化、大気中での散乱による赤化等の影 響が重なっている。それらはマスロス量の過大評価につながり。星数が多いと無視 できない。その相殺を行うため、τ の分布を負領域にまで伸ばしてヒストグラ ムを作る。 (図8を伸ばして青いカラーの星を負のτ とするのか?) 図14では、統計的に生にも負にも起きると考えた(大気散乱?)効果を差し引いて 本来のマスロスによる τ の分布に直した。 (どうして正負に対称な τ変化を起こ すのか理屈がさっぱり分からない。) スケーリング こうして得た τ と L からスケーリングでマスロス率を求める。図14のτ 分布の補正 f/fo, ここに f=補正後の数、fo=補正前の数、を行い総マスロスとする。 図15=総マスロス量 図15に各質量ビンごとの総マスロス量を示す。上は右側からの累積マスロス、下は 各ビンからの寄与である。 (さりげなく質量に移っているけど、 どうやってかはすっ飛ばしている。特に、AGB 先端に達していない星が多数あ るという描像下でどうやるのか?) 図には変光星からのマスロスと非変光星(低質量赤色巨星) からのマスロスを載せた。この後者=非変光星は数が多く、総計すると中間質量星や 赤色超巨星からのマスロスの数倍に達する。 |
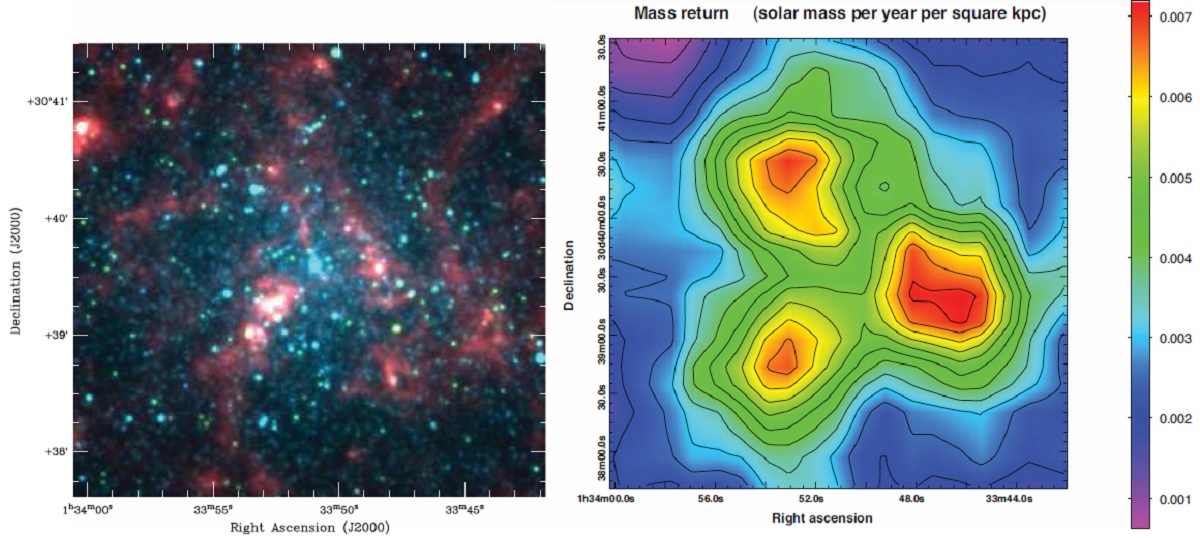
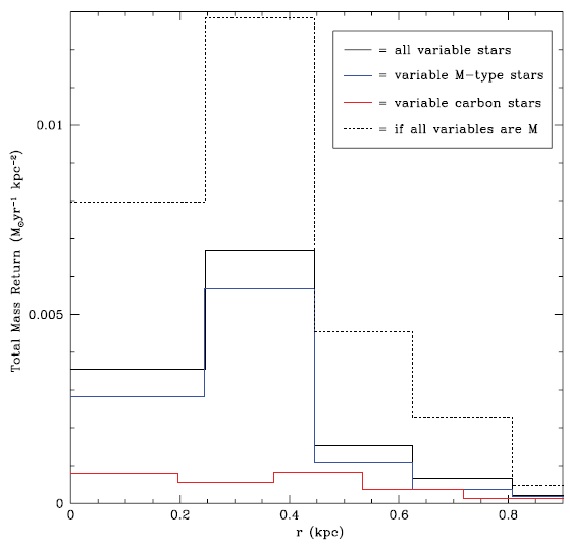 図16.マスロスの動径分布 ただし、星間赤化がそれらの星の赤さの 原因となる場合が多く、得られた値は上限 < 0.028 Mo/yr と見做すべきである。 真の還流値は変光星からの値 0.0055 Mo/yr に近いのではないか。 (赤色巨星が AGB の数倍という結果を捨てて る。すてる理由が安易過ぎる。) 見落としも少しはあるから、 0.006 - 0.01 Mo/yr が総マスロス率と考えられる。 マスロス寄与星 そうは言ったものの、低質量 M-型 AGBs はより高質量の星全てと同程度の寄与を していそうだ。それら高質量星で、高質量炭素星と RSGs はそれぞれ同じくらい に寄与する。低質量炭素星と高質量 AGBs からの寄与は少し落ちる。 これを星形成 時期に直すと、現在還流源は主に次の3つの時期に出来た星と考えられる。 t < 40 Myr t = [0.2, 1] Gyr t = [3, 10] Gyr これは、大体 Javadi et al. (2011) の SFH を反映していると考えられる。 炭素星からの寄与 炭素星からの寄与は 23 % である。つまり星間ダストは O-リッチと考えら れる。 星間還流の空間分布 星間還流の動径分布を図16に示す。炭素星還流は r < 0.5 kpc では 平坦であるが、 M-AGBs からの還流は数百 pc 以内で最高だが、 r = 0.3 - 0.4 kpc で大きく上に外れる。図17にはそれがもっとよく分かる銀河面 再東映はしていない、二次元マスロスマップを示す。そこには外れの原因が RSGs、スーパー AGBs であることがはっきり示されている。 |
|
放出質量と星質量 Javadi et al. (2011) の変光期間 δ を使うと、誕生質量に対する変光期間中に失われる質量 の比が計算できる。  (読者はもっと困惑させられる。 先を追う気がしない。) 星形成率とマスロス率 我々が求めた総マスロス率は 0.004 - 0.005 Mo yr-1 kpc-2 であり、これは最初に求めた星形成率 0.003 Mo yr-1 kpc-2 を上回っている。 しかし、他グループが定めた星形成率はもっと大きく、我々の総マスロス率は それらには及ばない。Kang12 は Hα, FUV, FIR などから決めた星形成 研究をレビューして、M 33 の中心 1 kpc 平方の星形成率を 0.03 - 0.04 Mo yr-1 kpc-2 とした。 この星形成率を採用すると、マスロスはファクター 6 - 7 で大幅に足りない。 他からの寄与 SNe, LBVs などを加えてもファクター 5 で足りないに変わるくらい。 |
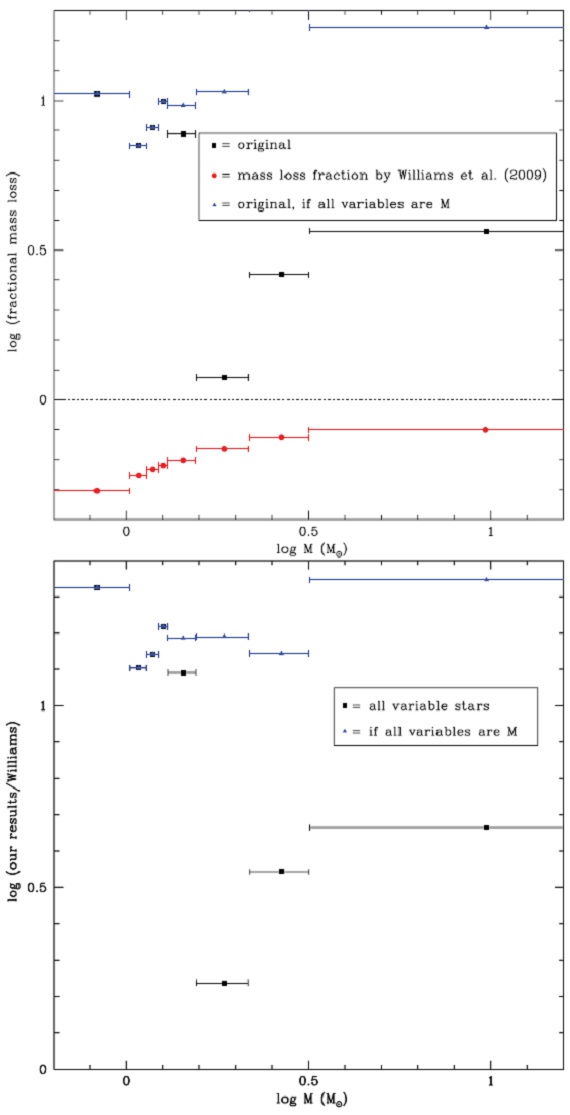 図18.上:脈動時期のマスロスと誕生マスとの比=失われる質量の割合。 水平点線=全てを放出。赤丸= Javadi et al. (2011) の IFMR。 下: 我々の出した総放出質量比率と IFMR との比。 |