|
新しいモデル TP-AGB の取り扱いが大幅に改善されたので、理論的等時線のはっきりした特徴 を提示出来るようになった。論文I Marigo, Girardi 2007 で述べた等時線の数を倍にし、熱パルス前の 静謐な水素燃焼時モデルには Girardi et al 2000 のものを使用した。その間の 年齢とメタル量に対する理論的等時線はグリッドの内挿で求めた。 AGB 星の特徴 我々は TP-AGB が保持する特徴、 (1)炭素星に適切なオパシティを適用して冷たいテールを形成させる、 (2)ホットボトムバーニングを経過する星がHR図上で釣鐘型の系列を成す、 (3)脈動モードの第1励起振動から基本振動への突然の転換、 (4)M- から C- 型に変わる際に起きる突然の重力低下が引き起こす質量放出 率の突然の増大、 を保持するよう注意を払った。 |
測光システムへの変換 等時線はを約20の測光システム、UBVRIJHKL から SDSS, OGLE, 2MASS, UKIDS などに変換された。マスロス星に対してはダストの影響も考慮された。 その結果、Spitzer, AKARI のような FIR, MIR 観測結果とも比較できるように なった。 測光システムへの変換 データは以下のサイトから取ってこられる。 http://stev.oapd.inaf.it/dustyAGB07 http://stev.oapd.inaf.it/cmd これらは、メタル量と年齢のどんな中間値に対しても表を与える。 |
|
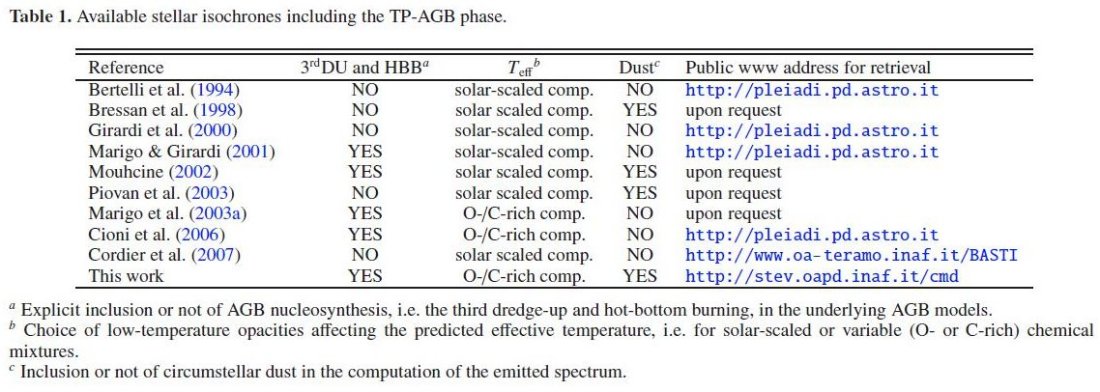
TP-AGB の役割 等時線の計算で TP-AGB 期は難しい。Frogel 1990 によると、TP-AGB は t = 1 - 3 Gyr では総光度の 40 % に寄与し、10 Gyr ではそれが 10 % に 落ちる。明らかに、TP-AGB は銀河の静止系 NIR スペクトルに大きな影響を 及ぼす。さらに、TP-AGB 星は銀河を星に分解したときの最も明るい天体 の大部分を占める。 各等時線の特徴 初期の等時線では TP-AGB は組み込まれなかった。最近の計算でも AGB の 扱いは粗い近似に頼っている。表1にこれまで公表された等時線を載せた。 簡単に言うと、Bertelli et al 1994, Girardi et al 2000 ではTP-AGB を 扱う際に、第3度ドレッジアップとホットボトムバーニング(HBB)を含めて いない。HBB による Mc - L 関係からの超過は Cordier et al 2007 では 扱われているが、第3ドレッジアップが入っていない。Marigo, Girardi 2001 は第3ドレッジアップを入れた初めての進化計算(Marigo et al 1999) に 基づいた等時線を示した。そして、 LMC, SMC の炭素星光度関数と合うよう 元素混入のドレッジアップ効率を調節した。Marigo et al 1999 進化計算の もう一つの特徴は HBB の効率が、モデル大気の有効温度と共に、外層構造の 積分から導かれたことである。 TP-AGB を不完全に取り扱ったモデル それ以外に、TP-AGB を含んで恒星種族進化合成を行ったモデル(Charlot, Bruzual 2003, Raimondo et al 2005, Vazquez,Leitherer 2005) は 多数あるが、TP-AGB 進化に欠かせない第3ドレッジアップ, HBB, 超星風 的質量放出、が無視されている。また、Charlot,Bruzual 2003, Vazquez,Leitherer 2005 では出典の異なるモデルを継ぎはぎしているので、 核の質量や外層の組成が非連続になっている。 |
銀河のスペクトル進化 銀河のスペクトル進化のために等時線を計算した例 (Bressan et al 1998, Mouhcine 2002, Piovan et al 2003) もあるが、 基礎になる TP-AGB モデルが よくない。 大気オパシティ それら全てで問題なのは TP-AGB 進化の過程で、オパシティが変化して行く ことを無視している点である。このため、有効温度決定に際し、太陽組成の 相互比を変えないままメタル量だけを変えている。これは非常に不正確な 結果をもたらす(Marigo 2002, Marigo et al 2003)。マゼラン雲の例では、 1.5 - 3.5 Mo の星 (t = 0.5 - 3.5 Gyr) は炭素星に変わる際に組成変化を十分 に考慮しなければならない。Cioni et al 2006 ではこの状況が部分的に 改善されている。その論文では、TP-AGB に沿って変化するオパシティが考慮 された等時線のセットが公開された。それらの等時線では炭素星は以前の 論文にあったよりずっと低く, Te = 2300 K まで、なっている。ただ、この モデルはその後に行われた Marigo, Girardi 2007 によるドレッジアップ効率 の較正の結果は組み込まれていない。この較正は、マゼラン雲の炭素星光度 関数とマゼラン星団における TP-AGB 期間を再現するように調整された。 論文の目的 この論文の目的は、上に述べた不満足な状況を是正するために書かれた。 ここでは、TP-AGB が第3ドレッジアップ、 HBB, オパシティ変化の3効果を 組み込んで作った等時線を示す。その効率値はマゼラン雲の結果を再現する よう調整される。その上、結果を様々な測光システムに使えるようにし、 さらにダストシェルの影響も加えた。 |

2.1.経路を合体させる第1熱パルスまでの進化この仕事で使われる進化経路は既に以前の論文に詳述されている。ZAMS から第1 熱パルスまでは Girardi et al 2000 に Z = 0.0004, 0.001, 0.004, 0.008, 0.019, 0.03 が、Girardi 2001 に Z = 0.0001 (http://pleiadi.oapd.inaf.it)が載っている。 質量範囲は Mi = 0.5 - 7 Mo である。その内、 0.5 - 5 Mo が熱パルスを経過する。 熱パルス期の進化 熱パルス期の進化は論文Iで述べた合成進化コードを使って計算した。そこでは、 第1熱パルスの物理条件から出発して、外層が完全に失われるまでが追跡される。この モデルでは TP-AGB 期の重要な現象、第3ドレッジアップ、HBB 光度超過と核反応、 熱パルスサイクルでの光度と表面温度変化、オパシティ変化、長周期変光、質量 放出、が考慮されている。 質量放出の定式化 特に重要なのは質量放出の定式化である。O-リッチな星では第1倍音振動か 基本振動かに注意しながら、 Bowen, Willson 1991 によるダストを含んだ動力学計算の結果を使用した。炭素星の質量放出に関しては 臨界光度に達する前はSchroder et al 2003 の半経験式を用いた。臨界光度に達する と Winter et al 2000, 2003 のダスト駆動型の脈動質量放出のモードに移ると 考えた。どちら |
も質量放出率は周期に依存する。その周期の値は Ostlie, Cox 1986,
Fox, Wood 1982, Wood et al 1983 の周期 - 質量 - 半径 関係から導かれる。 M ≥ 3 Mo 進化の変更 M ≥ 3 Mo 進化は論文Iから第1倍音と基本振動間の遷移光度を改良したため 変更された。詳細は付録に述べた。 post-AGB 進化 TP-AGB 進化の後には外層の完全な放出が続く。この時期は post-AGB 進化の かなりの部分を占める。この時期の進化は合成 TP-AGB コードの信頼性が薄い。 静謐期光度 等時線には熱パルス直前の静謐期光度と最低温度をつないで用いた。そうしない と等時線間の内挿が行えないからである。各熱パルス毎の光度、温度変化は 別に用意した表を用いて再現される。 つなぎ目 Girardi 2000 はオパシティに Alexander, Ferguson 1994 のスケール太陽を 使い、一方 Marigo, Girardi 2007 ではオパシティは組成変化に合わせてオパシ ティを計算し直している。しかし、第1熱パルスのつなぎ目ではその差は非常に 小さく、温度が僅かに上がる程度であった。 |
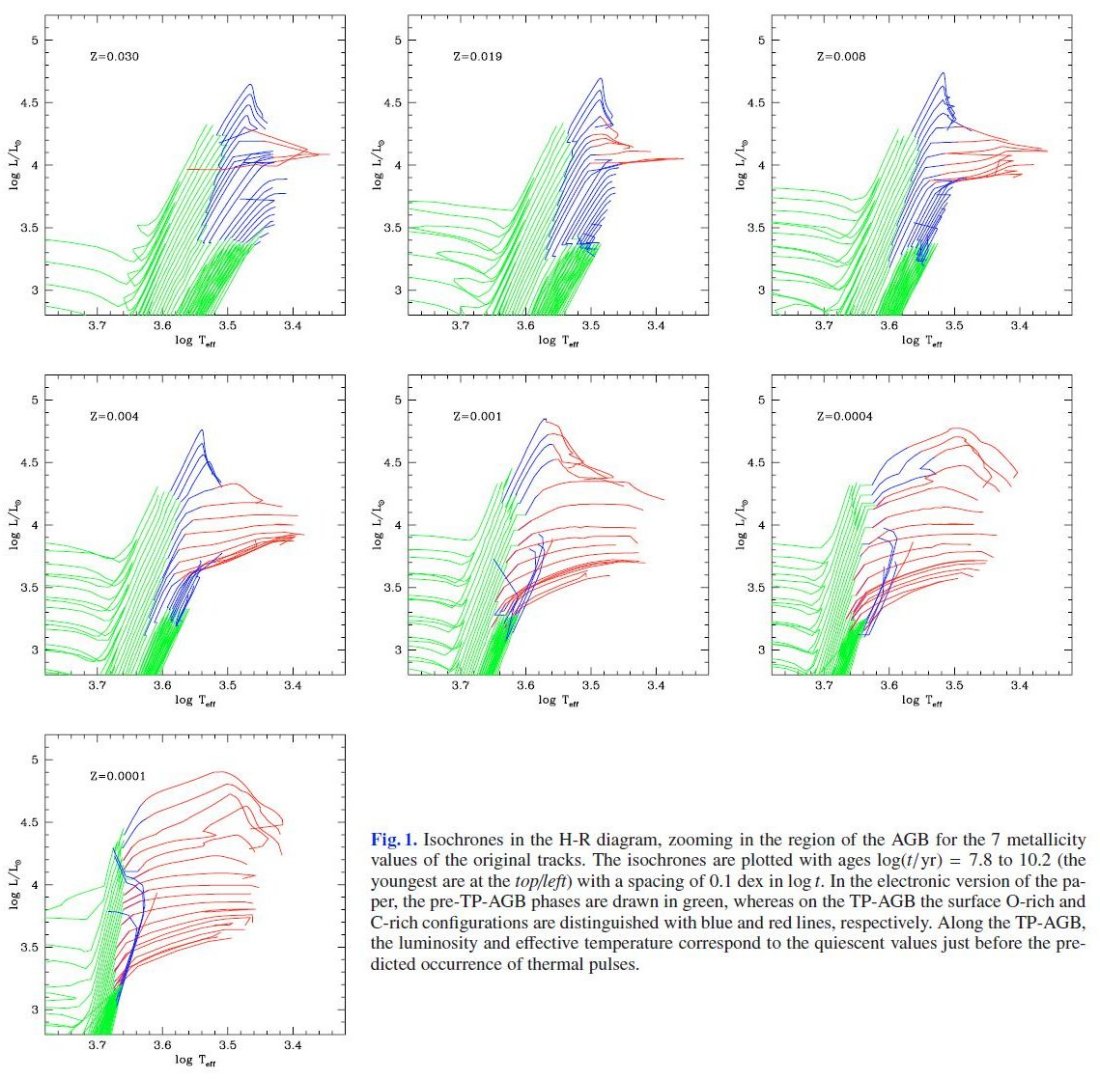
2.2.得られた等時線等時線の建設進化経路内の一次式での内挿により、必要な年齢での点が求まり、その点を つないで等時線が得られる。新しい TP-AGB モデルでは Girardi 2000 では 考慮していなかった、化学組成、コアマス、質量放出率などの色々な物理量 が入ってきた。これらは全て数値として与えられている。 早期 AGB 熱パルス以前の脈動と質量放出率は進化経路が決まった後でその温度、光度 を使って求められた。(L, Teff, Mi) から脈動周期と質量放出率を O-リッチ の熱パルス星と同じようにして求める。通常、質量放出率は小さく進化上の 影響は無視できる。しかし、低質量星に関しては赤色巨星枝先端 (TRGB) で Reimers 1975 の式を適用すると η = 0.4 で ΔMRGB ≤ 0.2 Mo の質量が失われる。この放出量は水平枝の形状を説明するため に必要な量である。計算の上では単純に質量 M のTRGB点からいきなり質量 M - ΔMRGB の ZAHB 点へジャンプさせている。 等時線サンプル 図1には広範な等時線セットが示されている。TP-AGB を拡大しているので、 全体を見たい場合は Girardi 2000 を参照せよ。図を見ると、TP-AGB 進化経路の 特徴が等時線にも反映されていることがわかる。興味深い点を挙げると: 中間 - 高メタル量 Z ≥ 0.004 最も若い年齢の星では HBB と高い質量放出率の結果、 TP-AGB 曲線は釣鐘型 となる。光度は初め HBB の効果でコアマス - 光度関係を上まわって急増し、その 結果起きた強い質量放出のため外層を劇的に減らし、HBB と超過光度の双方が 消滅する。 |
これらの星は通常 C/O < 1 である。しかし、HBB 消滅後の最後のドレッジ
アップの結果、炭素星が現れる場合があり、(Frost et al 1998) van Loon et al
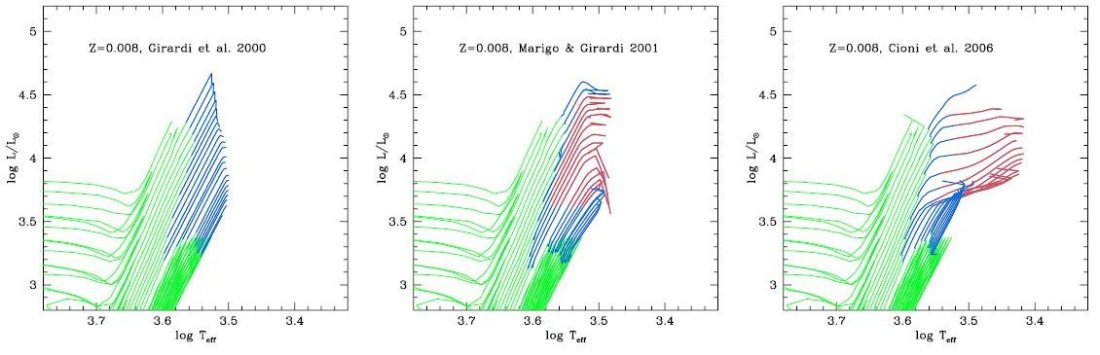
1998, 1999 の観測と一致している。 炭素星は中間年齢等時線で発達する。オパシティが全く変わる(Marigo 2002)結果 温度が 2500 K まで低下し、「赤い尾」を産み出す。 古い等時線ではドレッジアップは働かず、TP-AGB 線は単に早期 AGB の上に伸びる だけとなる。この単調な傾向は最後に外層質量が減った時にすこし左に曲がるまで 続く。 低メタル量 Z < 0.004 高中メタル量との大きな違いは、 HBB の効率にかかわらず、若い星にさえ 炭素星が存在することである。これは、ON サイクルが働いて O を N に変え、 そのため C/O が 1 を超すためである。 低メタル星の炭素星系列は高温度側で始まる。これは組成比が小さいためである。 最も古い O-リッチ系列は高メタルの時と同じように、高光度に進んでから高温度側 に曲がる。 以前のモデルとの比較 .今回のモデルが以前とどう変わったかを見るため、図2では Z = 0.008 の過去の 様々な等時線セットを並べた。左=Girardi 2000 は熱パルスまでを単に延長しただけ である。炭素星も HBB も見られない。 中= Marigo,Girardi 2001 はドレッジアップ+HBBが加わり炭素星が現れた。しかし オパシティがスケール太陽なので依然として早期 AGB を伸ばしただけになっている。 右=Cioni et al 2006 は可変オパシティを導入したので、形がはっきり曲がった。 だが、光度、寿命の較正がない。図1の Z = 0.008 との差を良く見よ。 |
測光システムへの変換は Girardi et al 2007 に述べられる。ここでは概略を。3.1.輻射補正と減光係数定義Fλ = 星表面でのフラックス、R = 星半径 Fbol = ∫ Fλ dλ = σTeff4 Sλ = フィルター透過関数 f0λ = 標準スペクトル、m0λ = 標準等級 BCλ = 輻射補正 輻射補正
|
辺々相差し引いて、(もっと直感的な導出があるかも知れない。) BCλ = Mbol - Mλ
計算した BC を使い Mλ = Mbol - BCλ が求まる。ここに、 Mbol = Mo,bol - 2.5 log (L/Lo) = Mo,bol - 2.5 log (4πR2Fbol/Lo) である。Girardi et al 2002 と同様、Mo,bol = 4.77, Lo = 3.844 × 1033 erg/s (Bahcall et al 1995) を採用した。 星間減光 この式には星間減光 Aλ を含むことも可能である。その場合は BCλ の式の中の Fλ を Fλ 10-0.4 Aλ で置き換える。 |
3.2.スペクトルフラックスの収集スペクトルライブラリーGirardi et al 2002 には広い範囲のスペクトルライブラリーについて述べてある。 それは、[M/H] = -2.5 ∼ +0.5, Teff = 600 ∼ 50,000 K, log g = -2 ∼ +5 である。それは、ATLAS9 "NOVER" スペクトル (Castelli et al 1997, Bessell et al 1998) が主要部をなし、M, L, T 型矮星は Allard et al 2000, Chabrier et al 2000 から、M 型巨星は Fluks et al 1994 の経験的スペクトル を用い、50,000 K を越える星は黒体輻射を使用した。 その後、ライブラリーは改訂された。ATLAS9 スペクトルは Castelli, Kurucz 2003 の "ODFNEW" で置き換えられ、分子、原子データが訂正された。特に、 CH, OH, SiO, H2wO, TiO のラインリストが直され、UV では HI-H+ と HI-H; 準平衡分子吸収線が加えられた。その結果、UV 領域ではずっと良くなり、 Teff = 3500 - 4500 K で波長全体に渡って向上した。 炭素星スペクトル その上、Loidl et al 2001 の炭素星スペクトル Teff = 2600 - 3600 K も 加えた。これは MARCS コードによる計算である。そこでは Teff ≤ 3200 K では、C/O = 1.1, 1.4, Teff > 3200 K では C/O = 1.1 のみ計算している。 Hofner 2003 も参照。2600 K以下の炭素星には単に 2600 K の輻射補正を適用した。 V より赤い波長では輻射補正は C/O 比に影響されにくい。Vバンドで C/O = 1.1 と 1.4 の間の差は 0.1 等以下であり、J バンドになると 0.01 等以下に落ちる。 波長が青くなると C/O 比の影響が大きくなる。B では C/O = 1.1 と 1.4 の 差が > 0.4 に達する。しかし、 Teff ≤ 3200 K の炭素星では B 等級は I 等級 |
に較べ、ベガシステムで 4 等以上暗く、実際の明るさに関し大きな興味は
持てない。そこで、この論文では全ての Teff に対し、 C/O = 1.1 でのスペクトル
を当てはめている。将来 Aringer et al の様々な C/O に対するスペクトルが
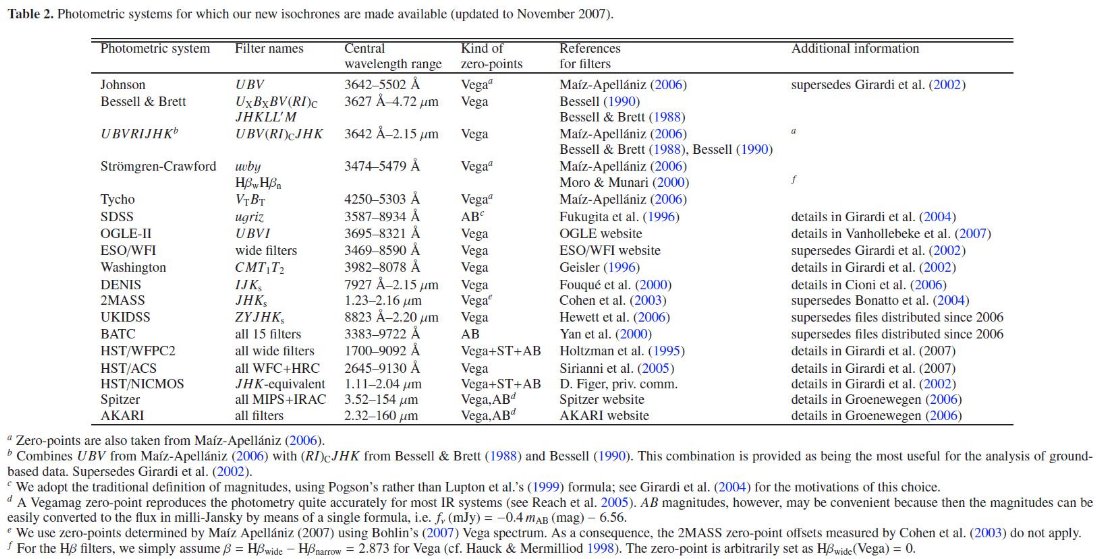
得られたらこの点は改善されるだろう。 白色矮星 TRILEGAL 計画の一環として、Finley et al 1997, Homeier et al 1998 からとり、Teff = 5000 - 100,000 K、log g = 7 - 9 のDA 星のスペクトル を収めた。 中間、遠赤外フラックス Castelli, Kurucz 2003, Allard et al 2000 はそれぞれ λ = 160, 971 μm までスペクトルを伸ばした。その他の仕事では中間赤外までしか伸びていない。 例えば、Fluks et al 1994 は 12.5 μm, Loidl et al 2001 は 2.5 μm である。 全ての場合について、計算最大波長の先はレーリージーンズ型で伸ばした。これが 粗い近似であることは明らかである。例えば、Bliek et al 1996 は太陽フラックスでは 黒体フラックスが遠赤外で 20 %の誤差を生むことを示した。Decin,Eriksson 2007 は 赤外フラックスの予告に関し研究した。それによると、我々の扱いは低温の M-, C- 星 では十分の数等の不確定性を持つ。カラーはもう少し小さいだろう。また、中間赤外、 遠赤外でフラックスの大きい質量放出星では大気放射は効かない。 3.2.フィルターセット表2にはここで考慮した測光システムを載せた。6.1.節に述べるようにその 値はWEBSITEから取ってこられる。 |
4.ダストによるフラックスの再構成星周ダスト星間ダストの供給源はAGB星と超新星と考えられている。Dwek 1998, Todini,Ferrara 2001, Morgan,Edmunds 2003, Calura et al 2007. 最近の Spitzer データ ( Lebzelter et al 2006, Verhoelst et al 2006) やモデル (Ireland, Scholz 2006, Woitke 2006, Ferrarotti, Gail 2006) は単純なシリケイト、炭化物の2分説では いかないことを示している。 動力学計算によると、炭素星ではダストにかかる輻射圧は観測される放出流を 説明するに十分なほど強い。 Winters et al 2000, Hofner et al 2003. しかし、 O-リッチ星では可能そうなダストは不安定で、また 1 μm 付近の吸光度が低く 放出流を説明できない。Ireland, Scholz 2006, Woitke 2006. ダスト成分と質量放出 LMC O-リッチ AGB 星 (Dijkstra et al 2005) やバルジ星 (Blommaert et al 2006) の ISO データ解析によると、ダスト成分と放出率の間に相関がある。例えば、 低放出率 O-リッチ星では Al2O3 が、放出率が上がると シリケイトが主要なダスト成分になる。これは Spitzer による 47 Tuc の観測 (Lebzelter et al 2006) でも確認された。一方炭素星ではダスト凝結の系列を 調べるには多くのファクターを考慮する必要があって困難である。(Speck et al 2006, Thompson et al 2006) この様な困難度のため、この論文では Groenewegen 2006, Bressan et al 1998 の処方に従った少数のダスト成分を考える。 |
4.1.方法ダスト外層の光学的深さ τここでは、等時線にダストの効果を組み入れる方法を述べる。(L, Teff)、 質量放出率 -(dM/dt)、ダスト速度 vexp、ダスト/ガス 比Ψ、 の星 の光学的厚み τ は、 τ(1μm) = Ad(-dM/dt) Ψ vexp-1 L-0.5 (4) ここに、 Adは主にダスト成分で決まる量である。 計算上の便宜のため、最初にパラメターセット(τ(1μm), Teff, L, ダスト 露点Tc, ダスト混合比) を Bressan et al 1998, Groenewegen 2006 から決めて、 参照モデルを計算しておく。次に、等時線に沿った各モデルに対し、対応する Ψ, vexp, L, Teff, Ad から式(4)を用いてダスト 外層を求める。 τ(1μm) が決まったダスト外層の減光と放射はシェルモデルの計算から 決められるので、最終的にダストシェル付きの星フラックス Fλ と ダストなしの星のフラックス Fλ,0 との比から輻射補正 ΔBCλ が決まる。 計算手順 以上をまとめると、 (1)光球の C/O 比に応じてダスト成分を決める。 (2)次節に従い、L, Teff, C/O, dM/dt から、 Ψ, vexp を決める。 (3)式(4)から τ(1μm) を求める。 (4)全てのバンドフィルター毎に、 ΔBCλ を計算する。 |
4.2.膨張速度vexp を決める諸パラメター膨張速度の計算には Elitzur, Ivezic 2001 のダストウィンドモデルを使う。 それによると、
ここに、(-dM/dt)-6 は 10-6 Mo/yr 単位の質量放出率、 L4 は 104 Lo 単位の光度である。 vexp のダスト/ガス比依存度は式中のパラメター A, B に含まれる。 A = 3.08 × 105 Tc34 QS σ222 χ0-1
ここに、 Tc3 は 103 K 単位のダスト露点、QS は 輻射圧有効率の有効温度 Teff で評価したプランク平均、QV は V バンド での光吸収有効率である。χ0 は下の比で定義される。
ここに、QP(T) は、温度 T で評価した光吸収有効率のプランク 平均である。 σ22 はダスト凝縮時における 10-22 cm2 を単位としたガス 粒子1個当たりのダスト断面積 σgas である。
上式で、 a はダストの平均半径 (cm)、ndust, ngas はダスト とガスの数密度 (cm-3)である。 ダスト/ガス比は
ここに、ρdust = (4/3)πa3ρ grain ndust であり、ρgas = AgasmHngas である。 |
Agas = 4/(4XH+XHe) はガスの平均分子量である。
これらの量を代入して、
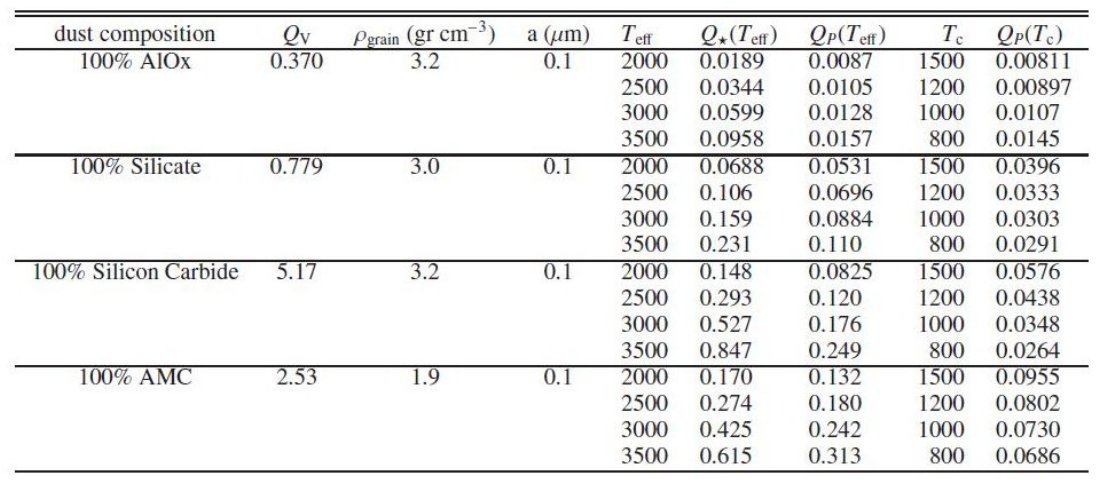
ちょっと注意しておくが、Elitzur, Ivezic 2001 では Ψ がフリーパラメ ターとして扱われている。4.3.節では Ψ を決める手続きを詳しく述べる。 Elitzur, Ivezic 2001 モデルで扱われる特性量 ダストの種類を決めると、Elitzur, Ivezic 2001 モデルに現れる量、QS, QP はダスト凝結温度 Tc、有効温度 Teff を選択すると固定 される。われわれは DUSTY (Ivezic 1999) を様々な ( Tc、 Teff ) の 組み合わせに対して計算して、QS, と QP を求めた。その 結果が下の表3である。 この論文では C/O < 1 に対しては Tc = 1000 K、 C/O > 1 に 対しては Tc = 1500 K を採用した。ダストの大きさは A = 0.1 μm に 固定した。 ダスト駆動星風による最低放出量 もう一つ注意しておくのは、式(5)が成立するのは、放出流を駆動するほどに ダスト形成が有効な場合のみであることである。Elitzur, Ivezic 2001 で論じ られているように、この条件は以下の最低放出率に対応している。
ここで、TK3 は 103 K 単位で測ったダストシェル内側境 界の運動学的温度である。簡単のため、TC = TK とした。 面白いことに、式(14)で与えられた -(dM/dt)min は Wachter et al 2002 が炭素星の動力学星風計算から与えた結果、-(dM/dt)min ∼ 3 - 5 × 10-7 Mo/yr とよく一致する。 ダストで駆動できない星風 -(dM/dt) < -(dM/dt)min の場合にはダストは星風を駆動できないが それでも星風内で受動的にダスト形成は起きるであろう。この様な場合を取り扱うため、 我々は膨張速度の式(5)内に入っている -(dM/dt) に -(dM/dt)min を代入して、膨張速度を評価した。 これが何を意味するのか見当がつかない。 この様にすると、 vexp は光度低下に伴って観測された最低星風速度 まで滑らかに下がって行く。もっと重要なことは、式(4)で vexp = vexp[-(dM/dt)min] を 実際の -(dM/dt) と組み合わせると 非常に薄いダストシェル,τ(1μm) ≤ 0.01 - 0.001, を取り扱えることで ある。 これも無理やりすぎて、根拠の見当がつかない。 式(5)の重要な特性の一つは、この式が自然に膨張速度の最大値を予言している 点である。この値は -(dM/dt) 大の時に、光学的に厚い星風で輻射カップリングが 弱くなる結果生じ、vmax = vexp(τ = 1.3) である。これ は観測データの解釈に際し非常に重要な意味を持つ。5.1.節を参照せよ。 |
4.3.ダスト対ガス比ダスト流出量ダストとガスのカップリングが完全、つまり両者の速度が同じ場合、Ψ = (dM/dt)dust/(dM/dt)gas である。Ferrarotti 2003, Ferrarotti, Gail 2006 によると、 (dM/dt)dust = Σi(dM/dt)dust, i (16) ここに、
ここに、Xseed はシェル内での種元素の質量比、Aseed は その原子量で、Adust,i はダスト種の平均分子量である。fdust, i は種元素の内ダストになった割合で、(dM/dt), C/O の関数として、 Ferrarotti 2003 から内挿して得た。 ダスト成分の境界線 AGB 星シェルの中でどのダストが形成されるかは C, O, Mg, Si などの元素の割合 に大きく左右される。我々は ZAMS ではスケール太陽の組成を仮定している。値は Grevesse, Noels 1993 から取った。進化の結果、C, O の量は変化するが, Mg, Si, S, Fe は不変と考える。 Ferrarotti, Gail 2006 のダスト形成計算に従い、二つの臨界炭素組成比、 YC,1 = YO - 2YSi と YC,2 = YO - YSi + YS とを 定義する。ここに、 Y = X/A は mol/g 単位の存在比である。この二つはダスト成分 を区分する鋭い境界を定義する。 |
YO が進化の間一定と仮定すると、 YC,1 と YC,2
から二つの臨界組成比 (C/O)1 = 0.90 と (C/O)2 = 0.97 が
決まる。O が不変であることは、ドレッジアップで上がってくる物質中の XO
= 0.5 - 4 % (
Boothroyd, Sackmann 1988 , Izzard
et al 2004) であることから保証される。しかし、この結果は対流層境界の取り扱い
方に大きく依存する。その上、HBB の効果によって O が減る可能性さえあることも
注意しておくべきである。しかし本論文では O 量が不変であるとして、ダスト成分を
(C/O)1 と (C/O)2 とで区分される3領域に対して考える。
これらは M, S, C 型星に対応する。詳細は 4.3.1.と 4.3.3.に述べる。 最大ダスト量 我々の等時線に以上述べたモデルを適用すると、Z = 0.019, 0.008, 0.001 の それぞれに対して、Ψ は O-リッチ星で 0.004, 0.002, 0.0001, C-リッチ星で 0.01, 0.02, 0.02 まで上がる。これらは予想される最大値であり、実際の AGB 星で 観測される量とは限らない。この問題は将来の課題である。 M型星では Ψ は Z に比例する。これは O-リッチ大気内ではダスト量を決める のは種元素 Si, Fe だからである。一方、 C-リッチ大気中では CO を形成した後の 超過 C 量がダスト量を決める。この量は第3ドレッジアップにより大きく影響される。 その結果、低メタル星でも大きな Ψ が達成される。 ダスト量の観測 van Loon 2000, Marshall et al 2004 は O-リッチ星において、Ψ ∝ Z で あることを観測から示した。また、van Loon et al 1999 は低メタル炭素星で分子形成 やダスト形成に使える炭素量が大きいことを示した。この点に関しては最近、Speck et al 2006, Thompson et al 2006, Sloan et al 2006, Zijlstra et al 2006, Lagadec et al 2007, Matsuura et al 2007 を参照せよ。 |
4.3.1. C/O < 0.9 の星十分な酸素原子があるのでシリケイトタイプのダストが形成される。二種類、 シリケイトと鉄ダストを考慮する。
ダスト凝結度 fSil は、オリビン、パイロキシン、コルツ型の和である。 fSil = fOl + fPy + fQu この時、シリケイトダストの有効分子量は、 ASil = (fOlAOl + fPyAPy + fQuAQu )/fSil Ferrarotti, Gail 2001 によると、この三者への分配は YMg/YSi に依存する。今回の YMg/YSi = 1.07 では主にオリビンと パイロキシンが形成され、それに少量のコルツが加わる。M-型星、-(dM/dt) = 10 -5 Mo/yr, YMg/YSi = 1.07 の場合には、 fOl/fPy = 4, fOl/fQu = 22 となる。 Ferrarotti 2003 は fSil, fIro を次の式で与えた。
|
4.3.2. 0.90 ≤ C/O < 0.97 の星この領域では、O が少ないため少量のシリケイトが作られ、大部分は鉄 ダストである。
Ferrarotti 2003 によると、
注意するのは、同じ(dM/dt)に対し S型星のシリケイトの凝結度の式の係数 0.1 が M型星の場合より低い。これは供給される O の量が小さいためである。fOl, fPy, fQu の比は M型星と同じにした。 4.3.3. C/O > 0.97 の星シリコンカーバイドと固体炭素の2種類のダストを考える。
Ferrarotti 2003 によると、
|
4.4.輻射輸達計算二つの輻射輸達計算この論文では Bressan et al 1998 と Groenewegen 2006 の二つの輻射輸達計算を 拡張した結果を与える。どちらの場合もモデルは1次元コードであり、輻射輸達の式 と熱平衡の式を並列して解いている。両者は細かい点での違いはあるが結果は非常に 良く似ている。例えば、 Bressan et al 1998 は Δlogλ = 0.04 で Fλ を与えているが、Groenewegen 2006 では与えられたバンド フィルターでの積分 Fλeff が与えられている点など。実際、 二つの計算結果の差 ΔBCλeff は τ(1μm) = 1 で 0.05 mag 程度である。 4.4.1.Groenewegen 2006 計算の拡張計算した星の有効温度等時線の中に組み込まれているダストモデルは Groenewegen 2006 から得た。我々は (勝手に)L = 3000 Lo, d = 8.5 kpc, vexp = 10 km/s, Ψ = 0.005 に対するモデル計算を行った。Groenewegen 2006 では数種類の有効温度に対する計算 しか行われていない。しかし、我々は M0, M1, ..., M10 に対する計算を Fluks et al 1994 の Teff = 3850, 3750, 3650, 3550, 3490, 3397, 3297, 3129, 2890, 2667, 2500 K モデルを用いて、 C/O = 1.1 炭素星に対して Loidl et al 2001 の Teff = 3400, 3200, 3000, 2800, 2650 K モデルを使って行った。組成は太陽である。 使用したダストモデル O-リッチ星では,(1) 酸化アルミ。ポラスな Al2O3。 Begemann et al 1997 の光学定数。(2)AlOX 60 % + シリケイト 40 % David, Pegourie 1995 光学定数。(3)シリケイト 100 %. 凝結温度は(1)、(2)で 1500 K, (3)で 1000 K とした。 炭素星では、(1)不定形炭素(AMC) 85 % + SiC 15 %, AMC 光学定数は Rouleau, Martin 1991, α-SiC 光学定数は Pegourie 1988。か (2) AMC 100 % のどち らかとした。凝結温度は(1)で 1200 K, (2)で 1000 K である。 |
計算範囲 この様な計算は -(dM/dt) = 10-10 - 4 × 10-5 Mo/yr、上に述べたスペクトル型 に渡った。この範囲に対応する光学的深さは、 AMC で τ(11.33 μm) = 3, AlOX で τ(11.75 μm) = 45 である。我々は90フィルターを考慮した。結果は ΔBC(τ) を表として 与えた。 4.4.2. Bressan et al 1998 計算の拡張スペクトルの形に効かないパラメターO-, C-リッチ、どちらも L = 104Lo, Te = 3000 K の星に τ(1μm) = 5 × 10-4 から 200 までをログ刻みで 50 ステップに変化させてダストシェルの計算を行った。Tc(O-リッチ) = 1000 K, Tc(C-リッチ) = 1500 K である。テストの結果、与えられたダストに対しては、ス ペクトルの形に対する L, Teff の影響は殆ど無いことが確認された。 スペクトルから L, Teff は決められない? しかし、 τ が薄い場合 Teff はもろにでるはずだが。 使ったダストモデル ダストシェルの輻射輸達は Granato, Danese 1994 コードを用い、球対称と r-2 密度分布を仮定して計算された。ダストのモデルは Rowan-Robinson et al 1986 : C-リッチでは AMC (a = 0.1μm), グラファイト(a = 0.03, 0.01 μm), O-リッチでは 非晶質シリケイト(a = 0.1μm), シリケイト(a = 0.03, 0.01μm) を採用した。 モデル計算の改善点 現在 Spitzer 観測に基づいてダストモデルの改良を進めている。新しい結果は 今後の論文で発表する。この論文では元のダストモデルのまま。 τ(1μm) と質量放出率の間の関係は式 (4) でシリケイトに対し Ad = 1.5 × 1011, 炭素質ダストで Ad = 6.6 × 1011、 として与えられる。Ad は中心星スペクトル Teff = 2500 - 4000 K により 5 % 程度変動することが計算から渡ったがこの程度の変化は許容される。 |
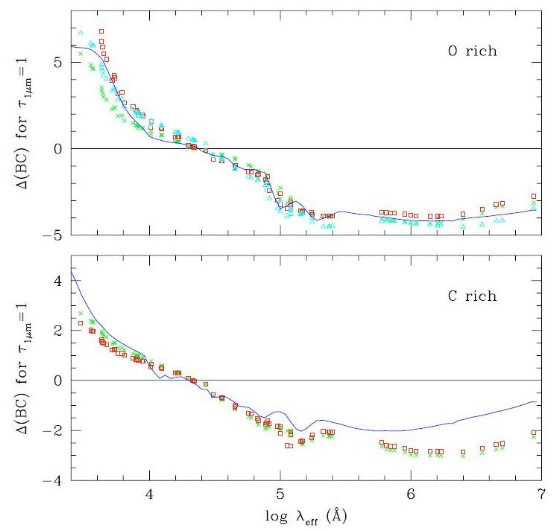
4.4.3.計算のまとめ図3は Teff = 3000K, τ(1μm) = 1 の場合の ΔBC を 波長の関数として表わしたものである。O-リッチ星の場合全てのモデルは 良く一致し、C-リッチの場合にも λ>10μm でかなり差が生じる がそれ以外では良く合っている。この差は τ が大きくなるにつれ拡大する。図3.用いたダストの吸収・放射特性を ΔBC(τ1μm =1, Teff=3000K) で表現した。 上:O-リッチ星。クロス=100%AlOX, 三角=100%シリケイト、 四角=60%AlOX+40%シリケイトのG06モデル。実線=B98 下:C-リッチ星。クロス=100%AMC,四角=85%AMC+15%SiCのG06モデル。実線= グラファイトのB98モデル。 |
 |
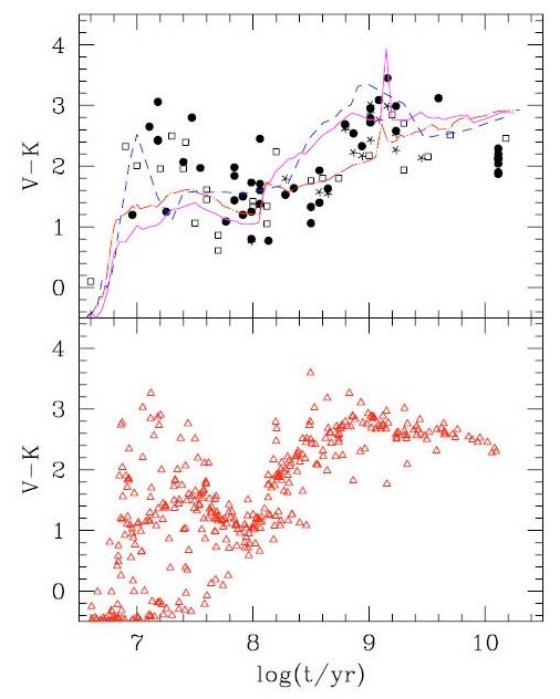
5.観測との予備的な比較等時線の提示に留めるということ文献では星種族の研究に Girardi et al 2000 がよく用いられている。それらは、 主系列、準巨星、RGB, レッドクランプ、E-AGB のような星の数が多いステージ を調べている。ここに、TP-AGB を赤外測光観測と較べる可能性を開いたので、 銀河系円盤とマゼラン雲データと比較してみる。 ただし、比較の大部分は今回の新しい等時線を見せるだけで、重要な問題、例えば 年齢-メタル量関係や星形成史のような、には踏み込まない。詳細な比較は今後の論文 に残す。 5.1.変光 AGB 星の膨張速度観測結果の図まず、膨張速度と周期の関係を調べる。その結果が図4である。O-リッチ星の P < 500 - 600 d では周期と速度の間に正の相関が見られる。しかし、それ 以上になると分散が大きくはっきりした関係は見られない。良く用いられる Vassiadis,Wood 関係は P > 500d でフラット(15 km/s)になっていて観測と 合わない。 釣鐘型の速度変化 図4下段には Z = 0.019, 0.008 に対する計算結果を示した。年齢に関係なく 全ての等時線は非単調な vexp - P 関係、初め増加し、続いて減少、 を示す。この釣鐘型曲線は若い、1.6 × 108 - 2 × 10 8 yr、等時線で特に良く発達している。この年齢は高質量(4.1 - 4.5 Mo) AGB 星に対応する。観測される長周期、低膨張速度変光星はこれに対応している 可能性がある。 OH/IR 星の膨張速度 これと関連して興味深いのは、log t = 8.3 で Z = 0.019 と 0.008 の二つの 等時線の比較である。Z = 0.008 の方が到達最高速度が小さい。LMC OH/IR 星で 観測された vexp は図4の速度減少域に対応している。これまで、銀 河系 OH/IR 星の膨張速度に較べ LMC のそれが小さいのはダスト対ガス比 Ψ が単純に Z に比例し、それが低 vexp の原因と考えられてきた。しかし、 図は vexp がL, M, -(dM/dt), Ψ などに複雑な依存をしていることを 示唆している。この点も将来の課題である。 |
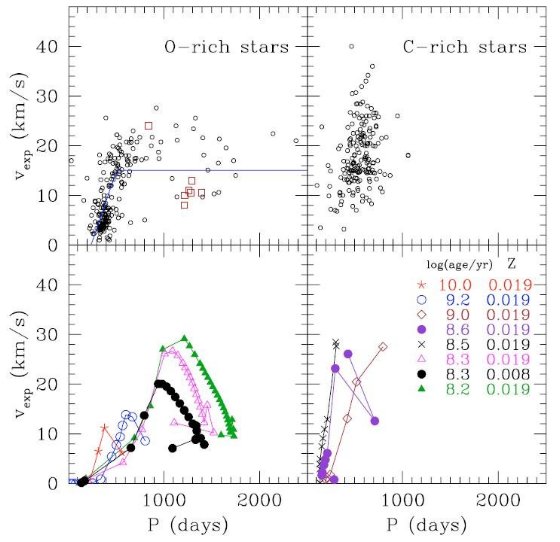 図4.変光 AGB 星の膨張速度。左=O-リッチ星。右=C-リッチ星。 上:白丸は銀河系(O-リッチはGro et al 1998. C-リッチはGro etal2002) 四角は LMC (Marshal et al 2004). 実線=Vassisiadis,Wood 1993 下:Z = 0.019, 0.008 の等時線に沿った膨張速度。数字は年齢。 |
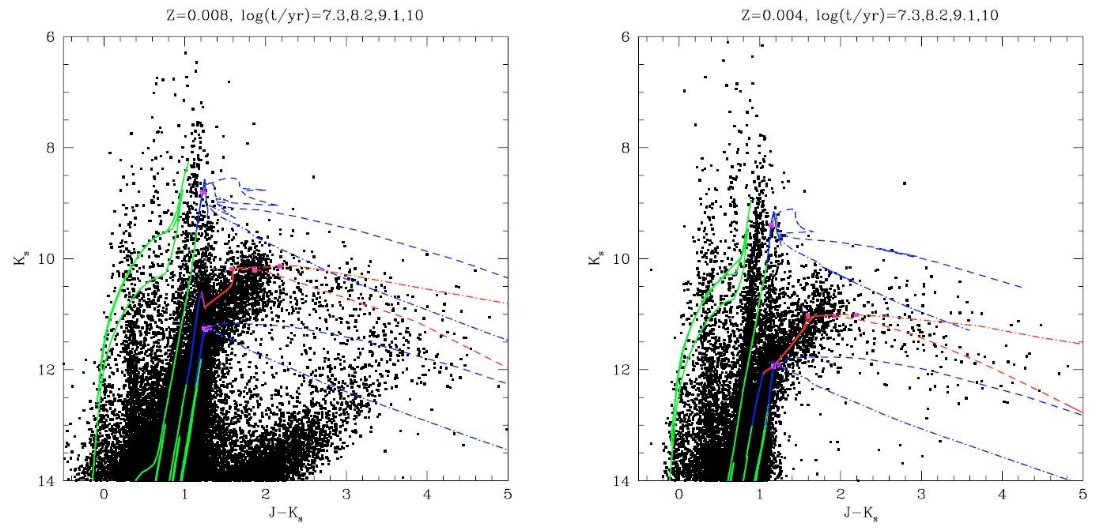
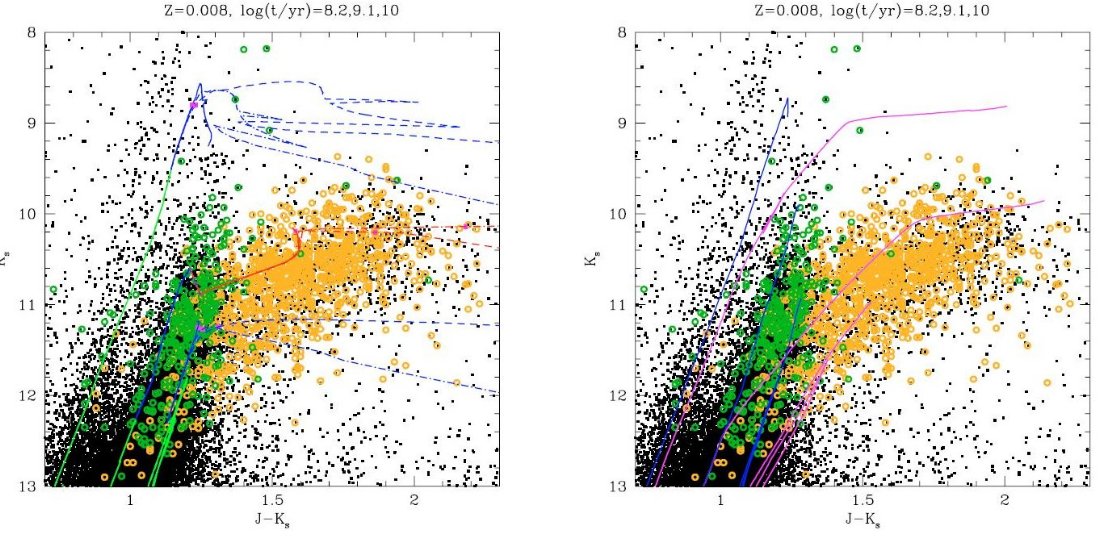
5.2.LMC, SMC の近赤外測光2MASS 色等級図図5には LMC, SMC の 2MASS K - J-K 図を示す。データは SAGE, S3MC カタログ から直接採った。Blum et al 2006, Bolatto et al 2007. したがって、Spitzer でも受かっている天体である。 LMC 外の天体 LMC のサンプルは α2000 = 5h23.5m, δ2000 = -69°45' を中心に半径1° の円からとった。この大きさだと LMC 以外の 特徴は弱い。それでも、(1)Ks < 11, J - Ks < 1.0 の垂直な指が銀河系 円盤とハロー星から。(2)Ks > 12, J-Ks > 1.6 の背景銀河の模様が見える。 等時線との比較 log t = 7.3 AGB 星は存在しない。Ks で最も明るい星は中心で He を燃焼している赤色超巨星 である。これらは Nikolaev, Weinberg 2000 の H 領域に対応する。 log t = 8.2 TP-AGB が良く発達し、明るい O-リッチ星が固まっている。これらは HBB | を 通過中の星である。これらの星は CMD 上で第2の対角系列をなし、 Nikolaev, Weinberg 2000 の G 領域に対応する。その下部は E-AGB 星からなる F 領域につな がる。 log t = 9.1 HBB は起こらない。TP-AGB はC-リッチ星の赤い尾で占められている。これは Nikolaev, Weinberg 2000 の J 領域に対応し、O-リッチ系列から Ks = 10.3, J-Ks = 1.2 で分離して J-Ks = 2 まで達する。この系列は log t = 9.1 の ダストなし等時線で大体よく再現されている。ただ、ダストなしなので J-Ks = 1.6 までである。このカラーは Loidl et al 2001 の Teff < 3000 K の炭素星 全てに該当する値である。 log t = 10.0 第3ドレッジアップは起こらない。TP-AGB は O-リッチである。これは Nikolaev, Weinberg 2000 の F 領域に対応する。TRGBのすぐ上である。 ダスト星の等時線 ここまでは弱い質量放出の領域で、ダストの効果は ≤ 0.2 mag であった。 -dM/dt > 10-6 Mo/yr でどうなるかは図によく示されている。 そこでは J-Ks = 4 まで次第に Ks で暗くなる系列が見えている。我々の等時線は この赤い尾の位置と傾きをよく再現している。 |
|
LMC CMD の詳細 図6にはLMC CMD 図5の拡大で TP-AGB が詳細に表わされている。さらに、 Groenewegen 2004 のOGLE + 分光データベースからM-,C-型LPV をプロットした。 M-型とC-型が CMD 上で分離していることが良く分かる。特に炭素星が J-Ks = 1.3 から 2 にかけて「赤い尾」を示し、M-型星が J-Ks < 1.3 に閉じ込められて いるのが著しい特徴である。 新しい等時線 図6の左右は新しい等時線がよく観測を再現することを古い等時線と較べて示す。 log t = 9.1 等時線では、ダストなしモデルでも J-Ks = 1.6 まで達し、(-dM/dt) < 10-6 Mo/yr の弱いダストシェルはさらに、Δ(J-Ks) ∼ 0.2 - 0.3 mag カラーを赤くし、 J - Ks = 1.6 - 2.0 の範囲をカバーする。 Marigo et al. 2003 に丁寧に解説してある通り、炭素星の「赤い尾」の原因は 第3ドレッジアップの結果、分子オパシティの変化に伴うTeffの低下である。 古い等時線 図6の右は Girardi et al 2000, Cordier et al 2007 の等時線を重ねてある。 これらの等時線は、第3ドレッジアップ、HBB を考慮していない。また、 Teff(L, M, Mcore) 関係はスケール太陽組成のものを使用している。これらの 等時線は以下の点で観測点分布の再現に失敗している。 |
古い等時線: Girardi et al 2000 Girardi et al 2000 等時線は O-リッチ AGB 星の経路を上手く説明する。これら の星は第3ドレッジアップの影響をほとんど受けていない。等時線は J-Ks ≤ 1.3 の領域に留まる。 古い等時線: Cordier et al 2007 Cordier et al 2007 の等時線は「赤い尾」の一部を再現して、 J-Ks = 2.1 まで 達している。しかし、それは O-リッチで log t < 9 の星である。これは観測と 合っていない。観測では炭素星のみが J-Ks > 1.3 に達する。 なぜ Cordier et al 2007 の O-リッチ星がそんなに赤くなれるのか?その理由は i) Wagenhuber 1996 の Teff 式を使用している。この式だと O-リッチでも 2400 K まで達することが可能である。 ii) カラー対Teff関係に炭素星(Bergeat et al 2001)を使用している。 ためであろう。しかし、Marigo 2002 の計算では O-リッチ星の Teff が 3000 K 以下 になることはまずないし、炭素星のカラー対Teff関係は O-リッチ星には適用できない。 SMC の色等級図 図5右図には SMC S3MC サーベイと重なる領域に対する色等級図を 示した。データの選択効果のためこちらの図には背景銀河がほとんど現れて来ない。 |
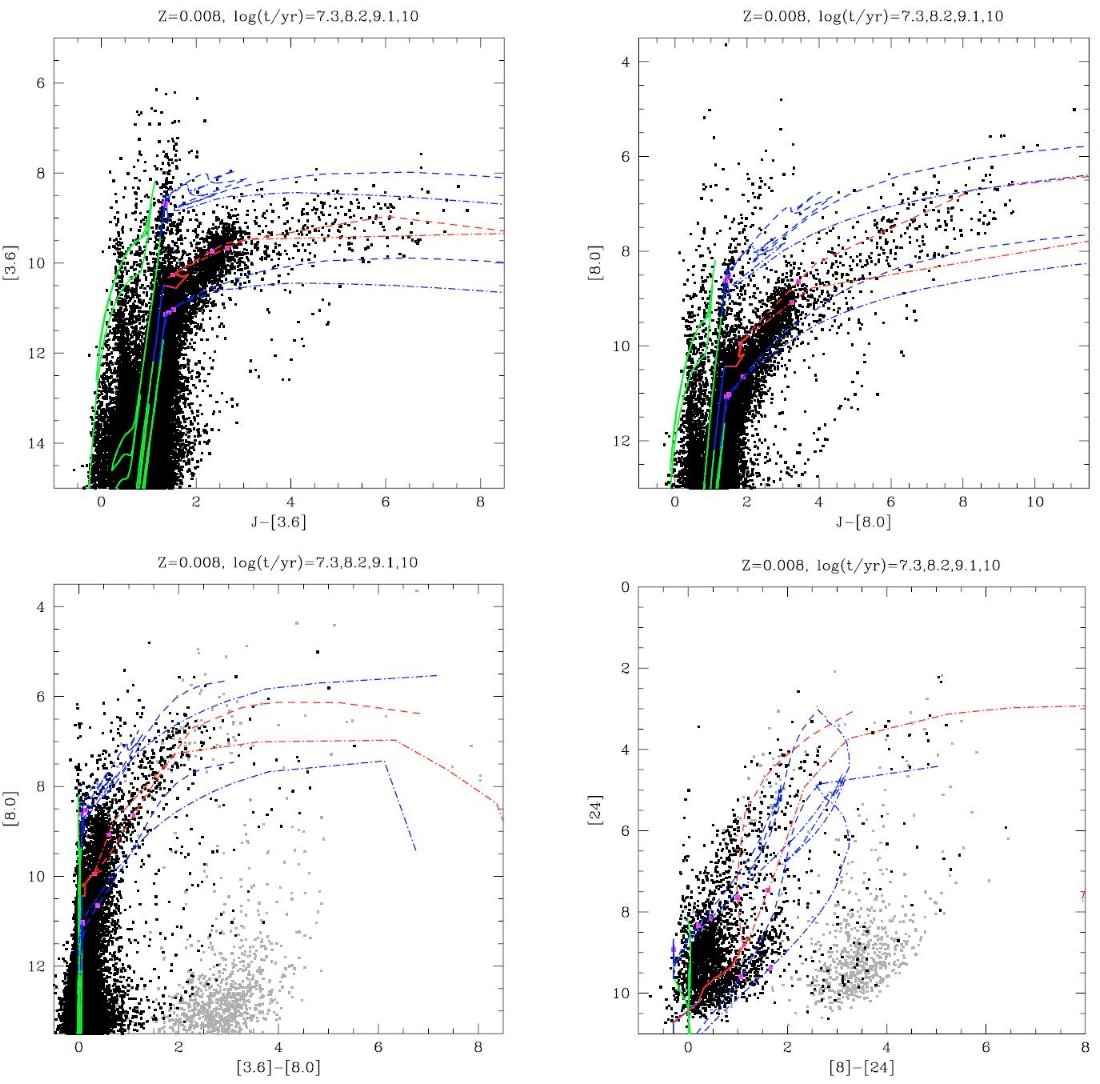
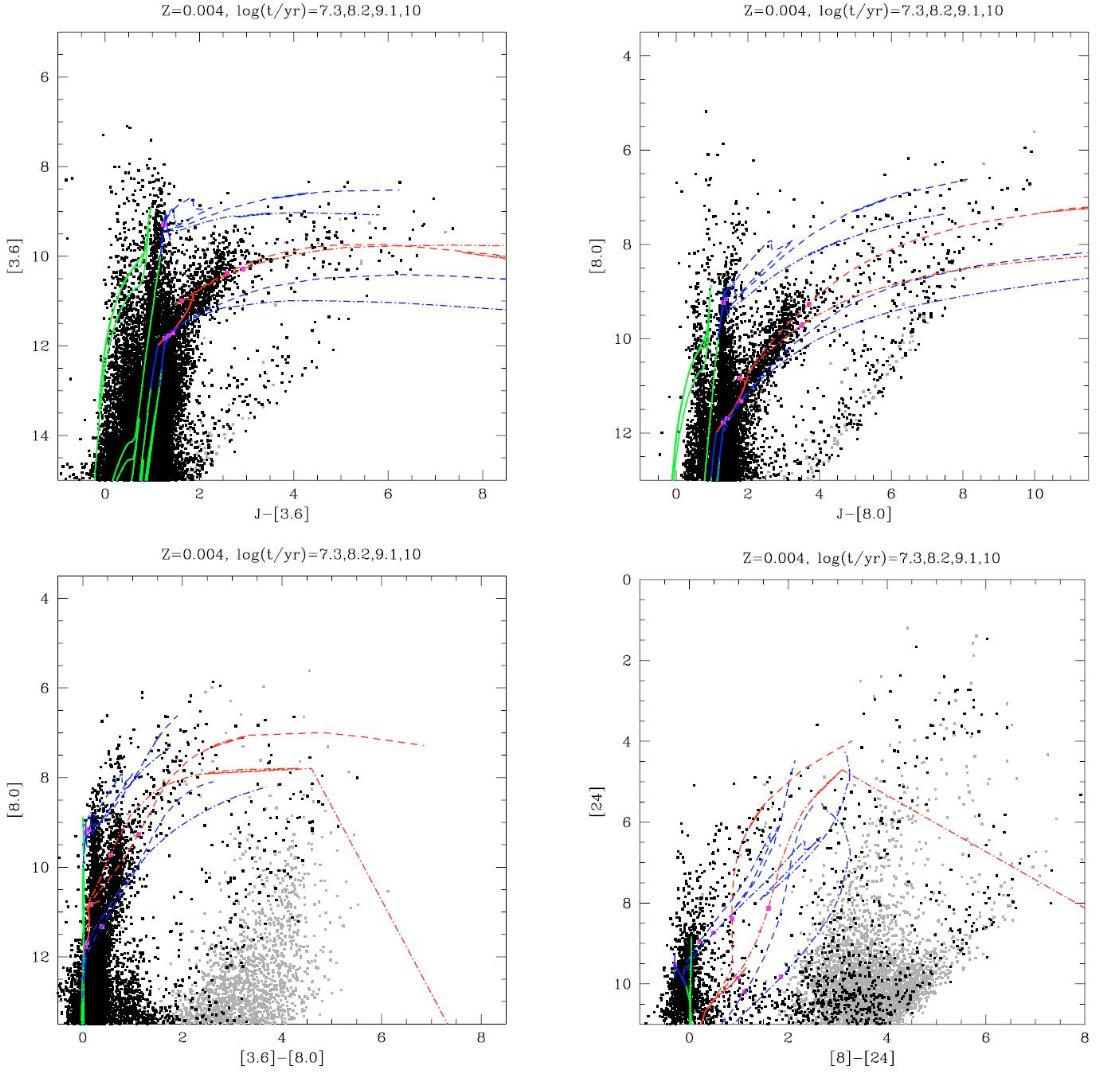
5.3.LMC, SMC の中間赤外測光図7と図8は LMC, SMC の近赤外、中間赤外測光の結果を 示す。SMC の S3MC データはフラックスで与えられているので、Cohen et al 2003 の JHKs と Bolatto et al 2007 の Spitzer バンドパスから等級ゼロ点 を決めた。星周ダストの効果は大きい。これらの CMD の特徴は基本的には近赤外と 同じである。特に、前景星の垂直な指が CMD の左側で著しい。図の右下には 背景銀河 |
の汚染が見られる。灰色の点は 2MASS で検出されなかった天体である。
それらの大部分は背景銀河と前主系列星であり、ここでは重視しない。 LMC の色等級図では、O-リッチ系列 (He 燃焼赤色超巨星と TP-AGB) が青い方 でほぼ垂直になることが判る。J-Ks < 2.0 の炭素星はここでも斜めに傾いた 系列として現れる。その端から高質量放出率の星の群れが淡く延びている。我々の 等時線はこれらの淡い系列も再現出来た。もっと重要なことはそれらが、炭素星だけ でなく、O-リッチ星からもなることを予言したことである。 |
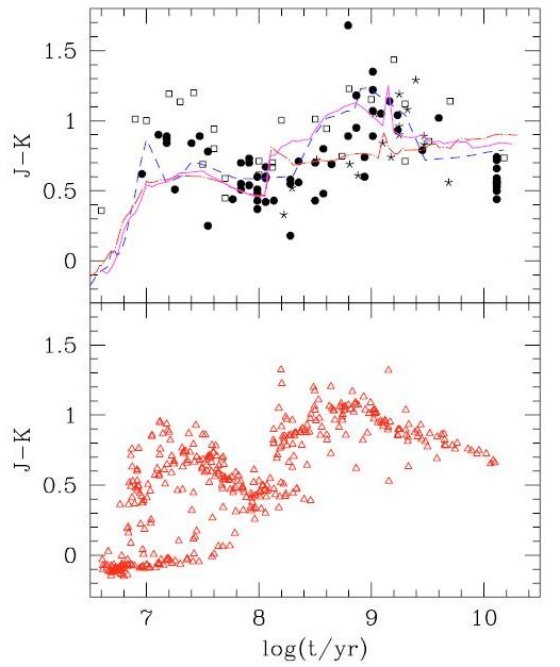
5.4.積分カラーTP-AGB のカラーへの影響どんな種族合成モデルでもまずマゼラン雲星団の広帯域カラーと較べて その性能を確認すべきである。図9には二つの積分カラー V-K, J-K を TP-AGB の影響が強く出るカラーとして選んだ。図9を見ると log t = 8 から先では 年齢と共に赤くなっていく傾向が見て取れる。これは SPP 内で TP-AGB が発達 して行くからである。付録Aを見よ。積分等級は熱パルスに伴う光度変化を考慮 して計算した。 他のモデル 比較のためこれまで広く用いられてきた SPP モデル、Charlot, Bruzual 2003 と Maraston 2005 を載せた。Charlot, Bruzual 2003 カラーは青いがこれは PT-AGB の比重が小さいためである。ただし、Bruzual 2007 の改訂を参照。 逆に Maraston 2005 は赤い方に片寄っている。我々の結果は中間である。 カラーシミュレーションの方法 図9の下段はシミュレーション星団を用いたカラー分布を示した。計算の方法は、 Chabrier 2001 の log-normal IMF に従って星を等時線に加えて行き、総質量が 一定値 MT に達した所で止めた。星団の質量分布は MT -1.5 を仮定した。これは、 Elson, Fall 10985 の LMC 星団光度関数から 導かれた。 ( Girardi et al. 1995 ) を参照せよ。星団メタル量は Pagel,Tautvaisiene 1998 の年齢-メタル量関係に 従うとした。星団年齢の分布は一定とした。この仮定は実際とは異なるが、 我々にカラー進化の様子を分かりやすく示してくれる。計算結果は 進化の進んだ星の数が少ないことに起因するストカスティックな変動が 星団にカラー分散を産み出す。そして、それは SSP 分布関数に基づく 連続カーブ(上図)より実際の姿に近い。 |
108 yr 付近での観測とのずれ モデルと観測との差が最も大きいのは 108 yr 付近で、計算は非常に青い星団の存在を予言したが、観測には 引っかからなかった。この青さは赤色超巨星が全く存在しないサンプルで見られる 現象で、赤色超巨星の寿命が非常に短いことから期待される予測である。観測される 若い星団のカラー分布を再現するには超巨星期が Bertelli et al 1994 より ずっと長くてTeff が低い必要がある。長くする一つの手はオーバーシューティング 効率を上げることである。しかし、そうすると高質量星のブルーループを小さく してしまう。Alongi et al 1991 参照。一方、赤色巨星の有効温度は外層最外側 大気に生じると言われている密度逆転層の取り扱い方により大きく変化する。この 問題の研究は将来の課題である。 TP-AGB 発達後に観測よりシミュレーションが赤い問題 もう一つの問題は、TP-AGB 発達後 108 - 4 × 108 yr 付近、に観測よりシミュレーションが赤い問題である。付録で述べるが、 この特徴を取り除こうとすると、最も高質量の AGB 星から He と N の増加を奪う ことになる。しかし、この点はタイプI 惑星状星雲の組成から必要とされている。 従って両者を矛盾なく説明することは難しい。 古い星団 古い星団では年齢 - メタル量関係の採用で最も古い LMC 星団のカラーが再現 出来た。これらは年齢、メタル量の点で銀河系球状星団と大体同じである。 まとめると 我々の等時線は良く使われる Charlot, Bruzual 2003 や Maraston 2005 と同じ くらいには星団テストをパスしている。その上、図9下段に見られるように、我々の 等時線は星団カラーの分布の様子も上手く表現出来ている。 |
 |
 |
6.1.データの表本論文で使用したデータは次の二つの形で供給される。(1)CDSカタログサービス: http://vizier.u-strasbg.fr URL: http://stev.oapd.inaf.it/dustyAGB07 等時線、輻射補正、吸光係数など。 (2)応答型ウェブサイト http://stev.oapd.inaf.it/cmd 指定した年齢、メタル量、測光システムで等時線を得る。 データに関する情報はケース(1)の場合は ReadMe ファイルに、ケース(2)の 場合は HTML help ページから得られる。データの範囲は、0.0001 ≤ Z ≤ 0.03, つまり、 -2.31 ≤ [M/H] ≤ +0.22, 及び 7.8 ≤ log t ≤ 10.2, つまり 63 Myr ≤ t ≤ 15.8 Gyr, 0.15 Mo ≤ M ≤ 7 Mo である。 その上、http://stev.oapd.inaf.it/cmd では、Bertelli et al 1994 の等時線を 使って、質量範囲を 100 Mo まで広げられる。これは年齢を 4 Myr まで下げることに 対応する。ZAMS に興味がある場合、t = 0 まですることも可能である。ただ、問題は それが Zo ≤ Z ≤ 0.03 に限定されることである。 表から得られる情報は、等時線に沿って、光度、有効温度、表面重力、要求した 測光システムでの絶対等級である。 TP-AGB に対しては、表面 C/O 比、脈動モード、 周期、質量放出率も加わる。TP-AGB かどうかはコアマスから判断される。炭素星か どうかは C/O 比から判る。 更新 最後に述べたいのは、サイトは常に更新されて行くことである。 6.2.最後のコメント低メタル星AGB 等時線は銀河系円盤とマゼラン雲に対してはかまり上手く合うよう調整されて いる。しかし、[Fe/H] ≤ -1.5 の低メタル星に関してはデータとの合致は未確認 である。 低温巨星の大気モデル 低温度星大気モデルはまだ不完全である。分子線のリストは不十分である。 LPV の動力学的モデル大気は M-, C-型星の静的大気よりよいエネルギー |
分布を
与えているようだ。 どういう意味なのか不明。 我々のモデルで用いた参照スペクトルのメタル量、有効温度、表面重力の範囲 は十分でない。 ダスト ダストの性質はここで用いたものと実際とは異なるかも知れず、等時線に沿って 変わっていくかも知れない。与えられたダストの成分に対して、輻射輸達の式に より様々な光学的深さのダストシェルの計算が行われた。銀河系ではおそらく、 10-7 Mo/yr 以下では AlOX, 10-7 Mo/yr 以上 ではシリケイトダストが適当であろう。メタル量によるこの境界への影響はこれから の課題である。 等時線 等時線を作るにあたり、内部整合性が破れる時がある。例えば、ダスト凝結の 取り扱いは動力学計算の過程とは整合していない。しかし、それらによる不確実さ の大きさは恒星進化のより基本的な問題に関する理解の欠如から来る不確実さに 較べると遥かに小さい。 これから マゼラン雲データは I から [24] までを包括的に扱う仕事が進んでいる。低 メタル量の矮小銀河、球状星団との照合は Gullieuszik et al 2007 その他で 進行している。低温度星大気の計算は Aringer et al により進められている。 まとめ 欠陥はあるが、我々の仕事は大きな進展を上げた。第3ドレッジアップが炭素星を 作り、ホットボトムバーニングにより高質量星が炭素星になる過程が阻害され、組成 変化に伴うオパシティ増加が炭素星の「赤い尾」を生む現象が考察された。質量放出 は O-リッチと C-リッチで分けて定式化され TP-AGB 最後の超星風も得られた。第1 倍音振動から基本振動への転換が予言され、それが質量放出の増加の引き金となる ことが議論された。第3ドレッジアップのパラメターはマゼラン雲炭素星の光度関数 とマゼラン星団のM-型星、C-型星寿命から較正された。膨張速度は過去の文献で用い られている単純なパラメター化の代わりに-(dM/dt), L, C/O, Z の関数として表わさ れた。 ダストによる再放射は長波長等時線の新しい研究を可能にする。 新しいモデルは、銀河系、銀河の恒星系のシミュレーションのためにTRILEGAL コードに含まれ、ダストを入れた放射モデル GRASIL コードはXから電波にいたる 銀河の積分スペクトルの研究に使用される。 |
|
3.0 ≤ M/Mo ≤ 5.0 の高質量星 TP-AGB 進化は以下のように改訂される。 マゼラン雲星団の積分カラー V-K, J-K, H-K を t ≥ 108 yr で 等時線モデルと較べると図A1 からわかるように、改訂前等時線カラーは 1- 4 × 108 yr で V-K の超過がある。t = 108 yr での V-K =2.5 への突然のジャンプは Mi = 5 Mo で縮退電子核が初めて形成される 事件に対応している。その先 1- 4 × 108 yr では積分 V 光度 はターンオフ近くで集まっている星が基本的に決めている。一方 K バンドは 最も高質量 AGB 星 3 Mo ≤ M ≤ 5 Mo から来る。 したがって、V-K のジャンプは高質量星 TP-AGB 期の過大評価が原因であろう。 これは、(a).星の光度が高すぎるか、 (b). 寿命が長すぎるかである。勿論、 二つは相互に関連する。というのは両者ともに HBB と質量放出に大きく影響される からである。質量放出率の不定性を考えると、モデル質量放出率が小さすぎるのが 問題のように見える。簡単な扱いは Reimers 則の η のように倍率をかけること である。 しかし、Fox, Wood 1982 の 3 - 6 Mo 非断熱脈動計算の結果を調べた結果、 Marigo et al 2007 では第一倍音から基本振動への転換光度が高すぎたことが 判った。この光度は第1倍音と基本振動との成長率が等しくなったところで決めた。 この元になった脈動モデルは 0.8 - 2.0 Mo の Ostlie, Cox 1986 であった。それを フィットして以下の式を得た。 log(L1-0/Lo)MG07=-14.516+2.277log(M/Mo) +5.046logTeff-0.084log(Z/0.02) 図A2 では実線=上の式を全質量領域に外挿した曲線が示されている。M = 3 Mo では この曲線は Fox,Wood 1982 と一致している。しかし、M = 6 Mo では Fox, Wood 1982 の結果を大きく外れている。この結果に基づき、M ≥ 3 Mo では log(L1-0/Lo)=log(L1-0/Lo)MG07 +ΔlogLcor ΔlogLcor = -0.125(M/Mo - 2.5) という補正を行った。図2A2 にはこの補正 L1-0/Lo を破線で描いた。 これが粗い補正であることは確かであり、より精密な研究が必要である。しかし、 この補正で 3 Mo ≤ M ≤ 5 Mo の TP -AGB 進化が計算し直された。その結果 大規模質量放出がより速く開始され、TP-AGB 寿命を縮めた。その結果は図A1 に 見るように満足すべきものである。 強調しておきたいのは t ≥ 108 yr での TP-AGB 燃料を任意に 切り捨てることはできない。なぜなら、さもないと例えばタイプI惑星状星雲から の核合成上の制約を満足させられないからである。それらは高い He, N 比を持ち、それはより高質量の HBB の結果と考えられている。この期間をあまり 短くすると観測されるほど高い He, N 組成に達することができない。 |
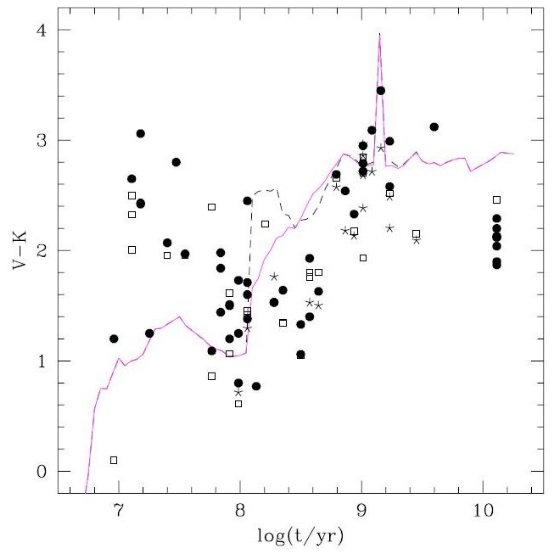 図A1. 星団の積分 V-K 対 SSP 年齢。Marigo et al 2007 より。破線=改訂前の TP-AGB 経路。実線=M≥3Mo改訂後の TP-AGB 経路。Z=0.008 を仮定。 観測データは Persson et al 1983(黒丸)、Kyeong et al 2003 (四角), Pessev et al 2006(星) 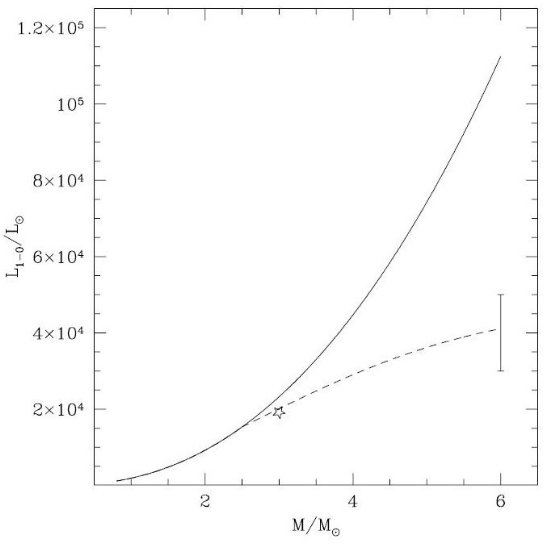 図A2.第1倍音から基本振動への転換光度。Z = 0.008 , log Teff = 3.52 仮定。 実線=改訂前の光度。破線=改訂光度。 星=Fox,Wood 1982 Mi=3Mo,Z=0.019, log Teff = 3.49 モデル。 縦棒=Fox,Wood 1982 6Mo モデル |