|
TRILEGAL コード TRILEGAL = 銀河系のあらゆる方向での測光をシミュレートする種族合成コード を説明する。このコードはスターカウントモデルの幾つかの技術的な点を改良した。 それらは、 （１）星の進化経路ライブラリーを完全なものとした。 （２）あらゆる測光バンドに対応する星のスペクトルライブラリー （３）ライブラリー入力変化や内容の記述が分かり易く変更が楽。 較正の変更 Groenewegen et al 2002 ではこのコードを始めて応用して CDFS 星カタログ を解析した。ここでは、 EIS の深い探査、 DMS 星計数に初めて応用する。これら はハローと大きなスケール高を持つ円盤成分を含んでいる。これにより得た、 もっと広い測光データを扱うために必要な較正の変化を示す。 |
2MASS とヒッパルコスへの応用 新しい較正に基づき、やや浅い 2MASS カタログを上手く解釈できることを 示す。このカタログは主に中間年齢円盤を探査している。また太陽近傍を調べた ヒッパルコスの絶対等級対カラー図を解釈した。この図には深いサーベイに較べ 高い割合で若い星種族が含まれている。 合わないところもある 同じモデル較正が上述の全てのデータセットにうまく応用できた。それらは 非常に深い CDFS (16<R<23) から、非常に浅いヒッパルコス (V<8) にまで及んでいる。ただし、銀河中心方向に対しては 50 % 以上のずれが生じた。 これはバルジ成分を含めていないためである。それと銀河面 ( おい！) 及び銀河南極方向でも良く合わない。TRILEGAL コードは可視ー赤外の広範囲サーベイ に使える形で提供されるであろう。 |
|
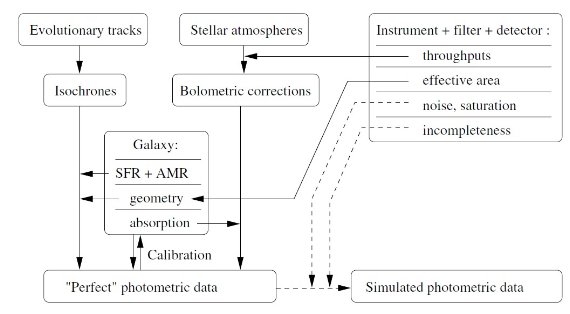
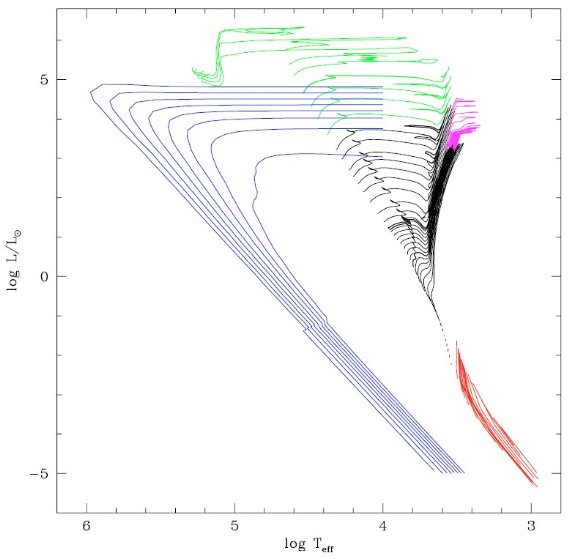
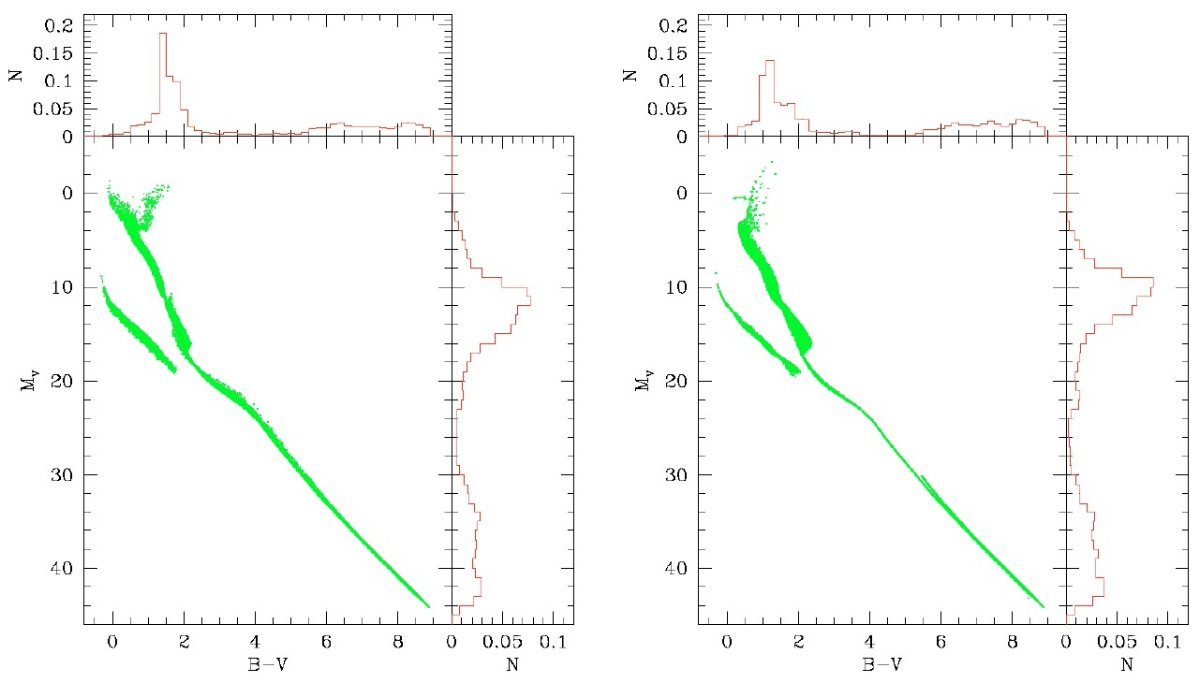
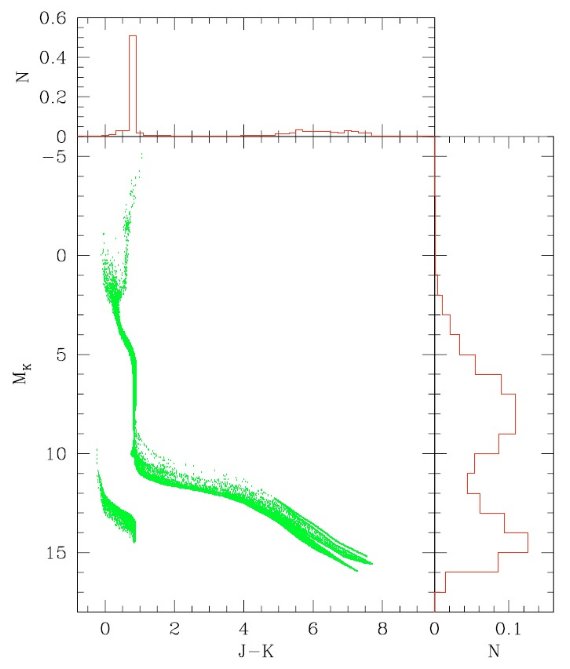
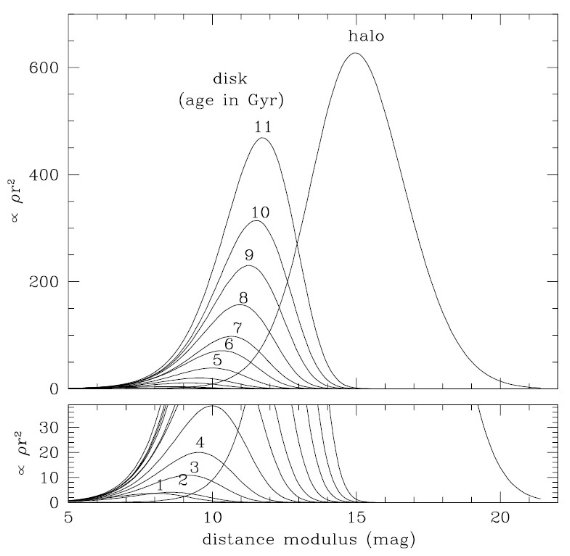
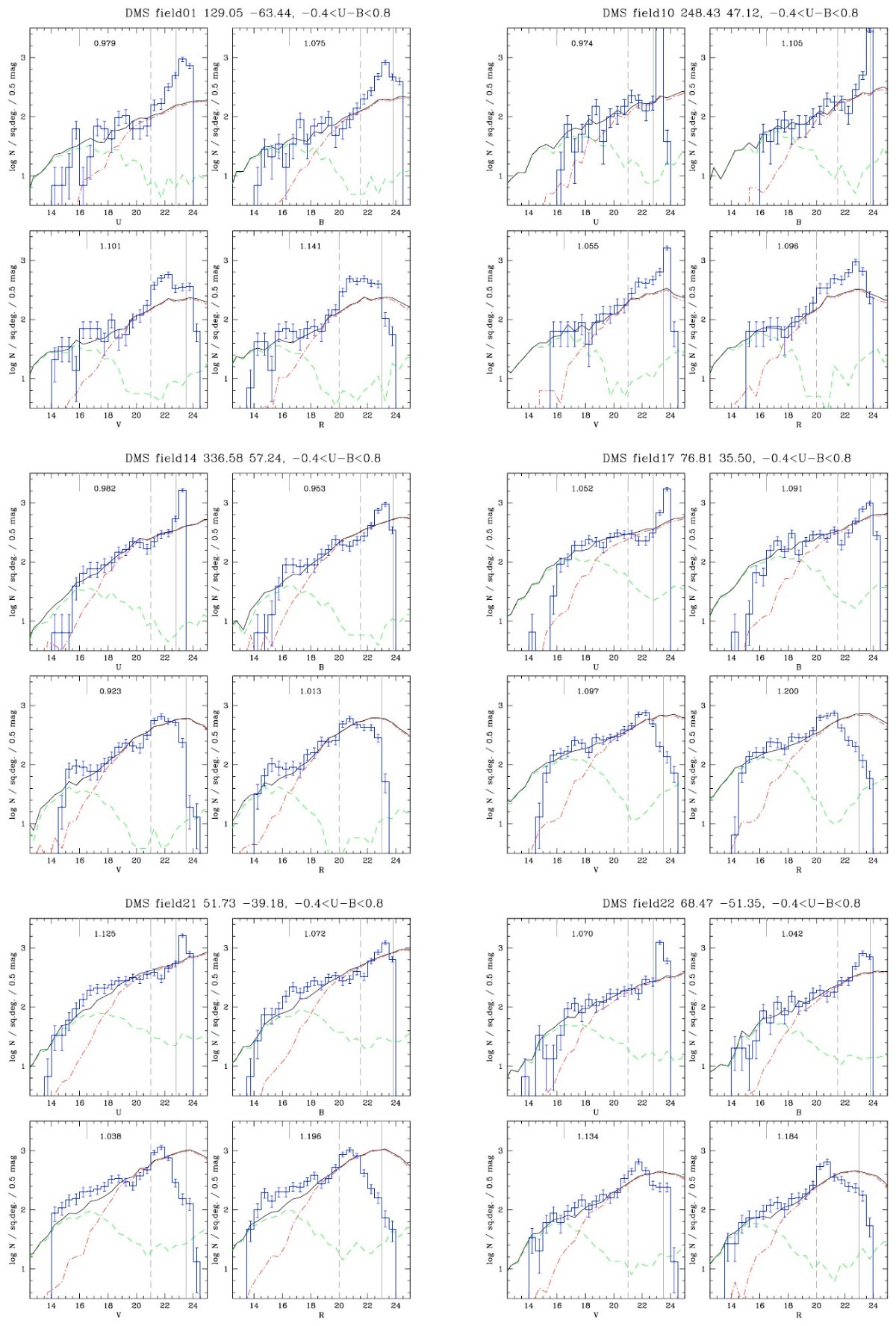
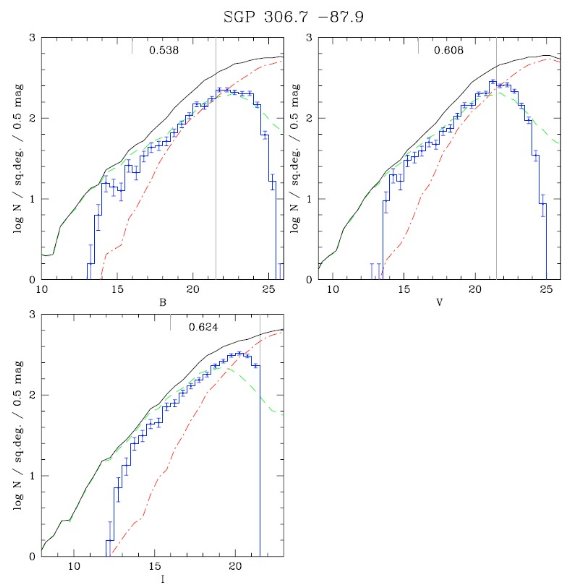
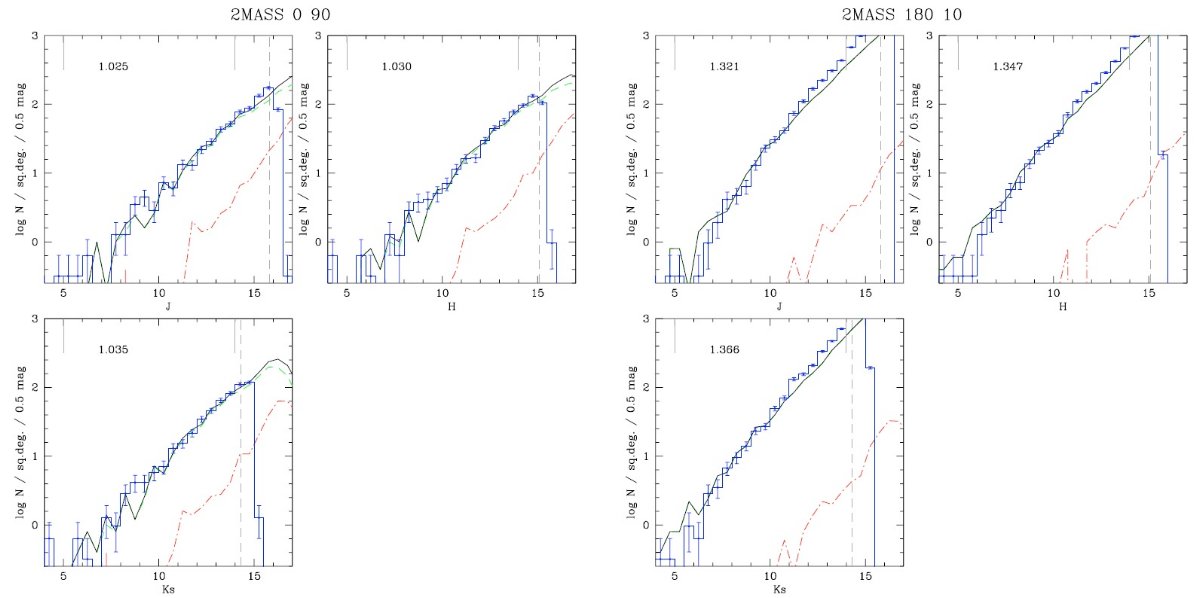
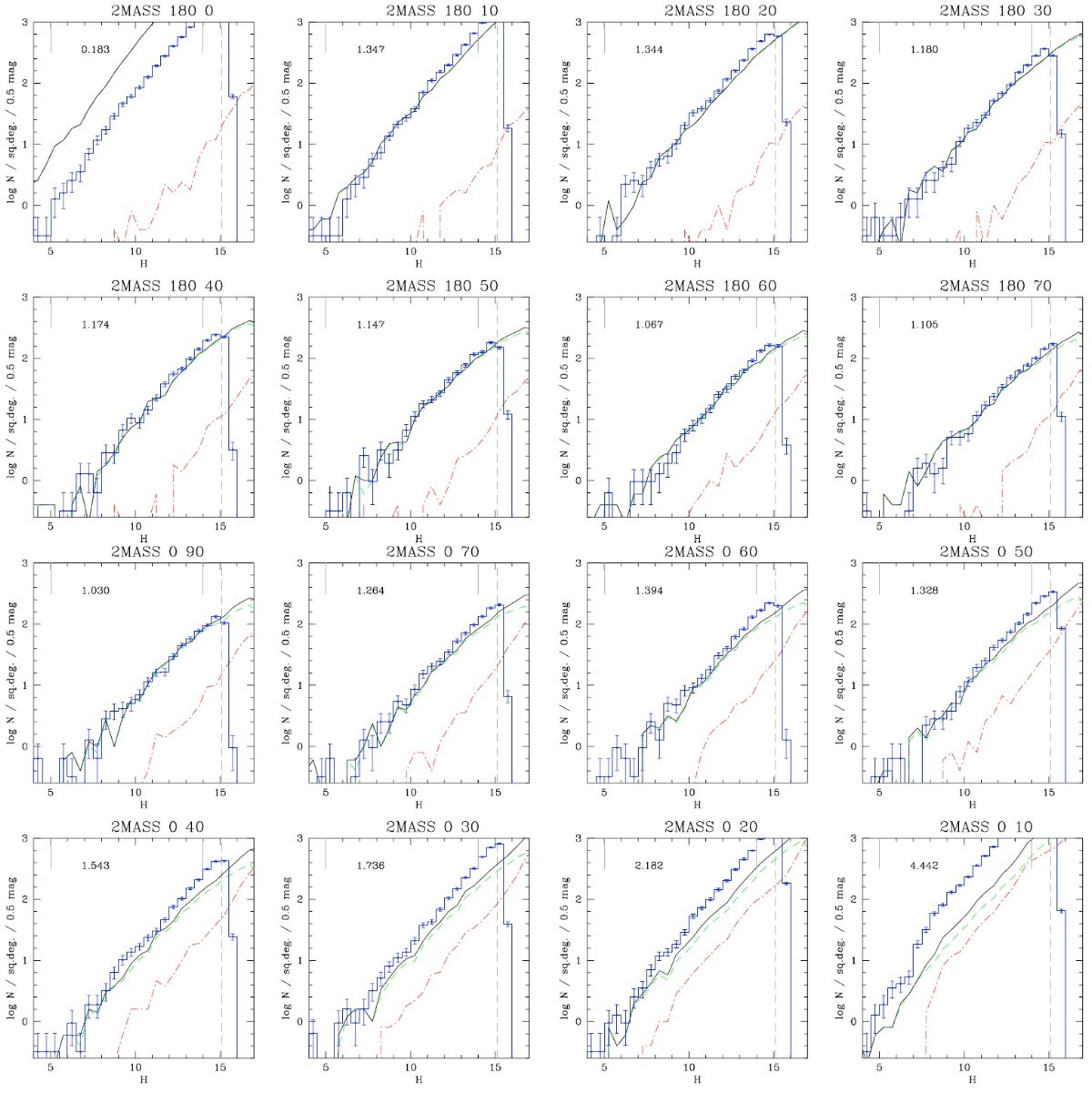
星計数の基本式 立体角 dΩ, 見かけ等級 dm 内に観測される星の数 N は N(m, l, b) = dmd&Omaega;∫dr r2ρ(r)φ (M, r) (1) M = m 5log r -A(r) +5 (1)' である。φ(M, r) は距離 r の地点での光度関数である。 (∫ φ(M, r) dM = 1 ？) ρ(r) と φ(M, r) の決定は星計数の終局目的である。そのための通常の方法は、 ρ(r) と φ(M, r) の関数形を仮定して、式(1)で計算した N(m, l, b) を 銀河系の幾つかの領域で得られた星計数データと比較することである。 よく使われる仮定（１）銀河系は３成分 &roh; = &roh;d + &roh;h + &roh;b よく使われる仮定（２）LF は場所で同じ φ(M,r) = φ(M) を上の各成分毎に考える。その際、（１）球状星団や太陽近傍から 得た観測光度関数を採用する方法と、（２）星の年齢、質量、メタルの分布と進化計算から 得られる理論的 φ(M)との二つの方法がある。 観測的光度関数の問題点 観測的光度関数は過去多くの研究で採用され、いくつかの研究が失敗した原因と なった。成功した場合でも霊異記間での不一致が見られる。よく使われた近似は、 円盤星のスケール高が M により異なる、つまり異なる ρd を持つ。 Bahcall, Soneira 1980, Bahcall, Soneira 1984, それにその後の多くの研究では Mv > 5.1 矮星に 325 pc, Mv < 2.3 矮星に 90 pc を割り当て、中間等級は直線内挿で近似していた。 |
これは若い種族と古い種族を大雑把に分離するものと解釈される。赤色巨星は 250 pc
のスケール高と仮定された。
Gilmore, Reid 1983
は主系列星に同様な近似を採用した。
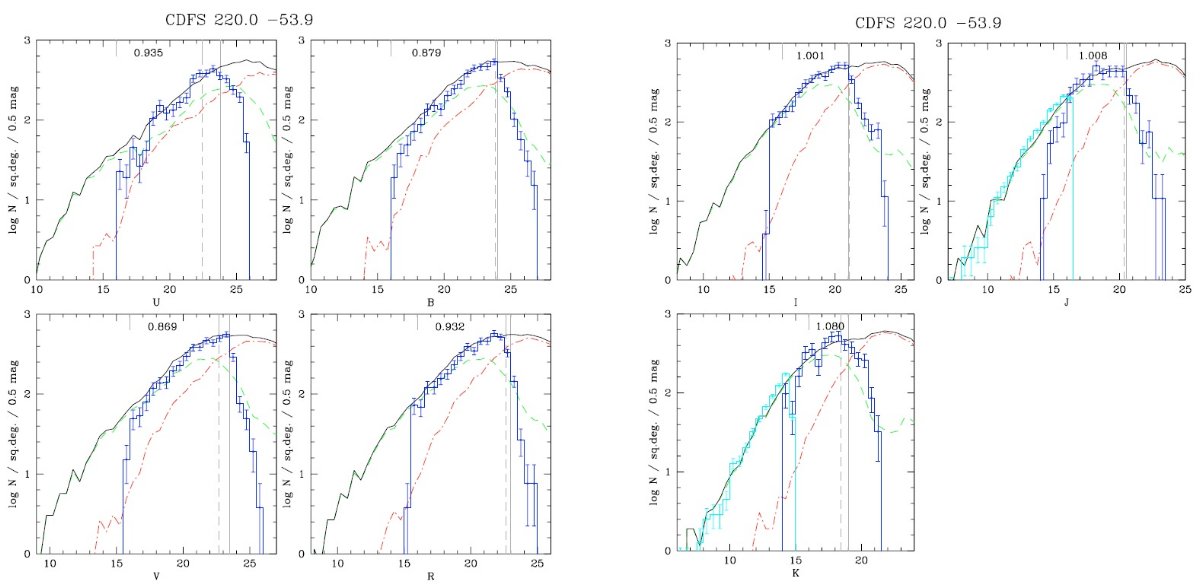
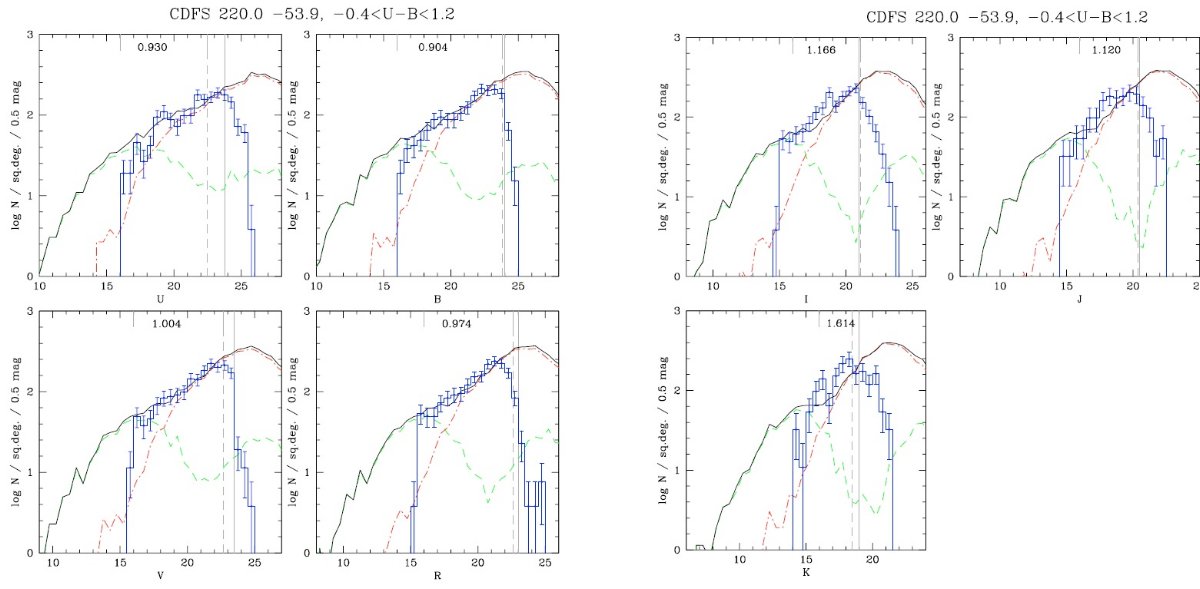
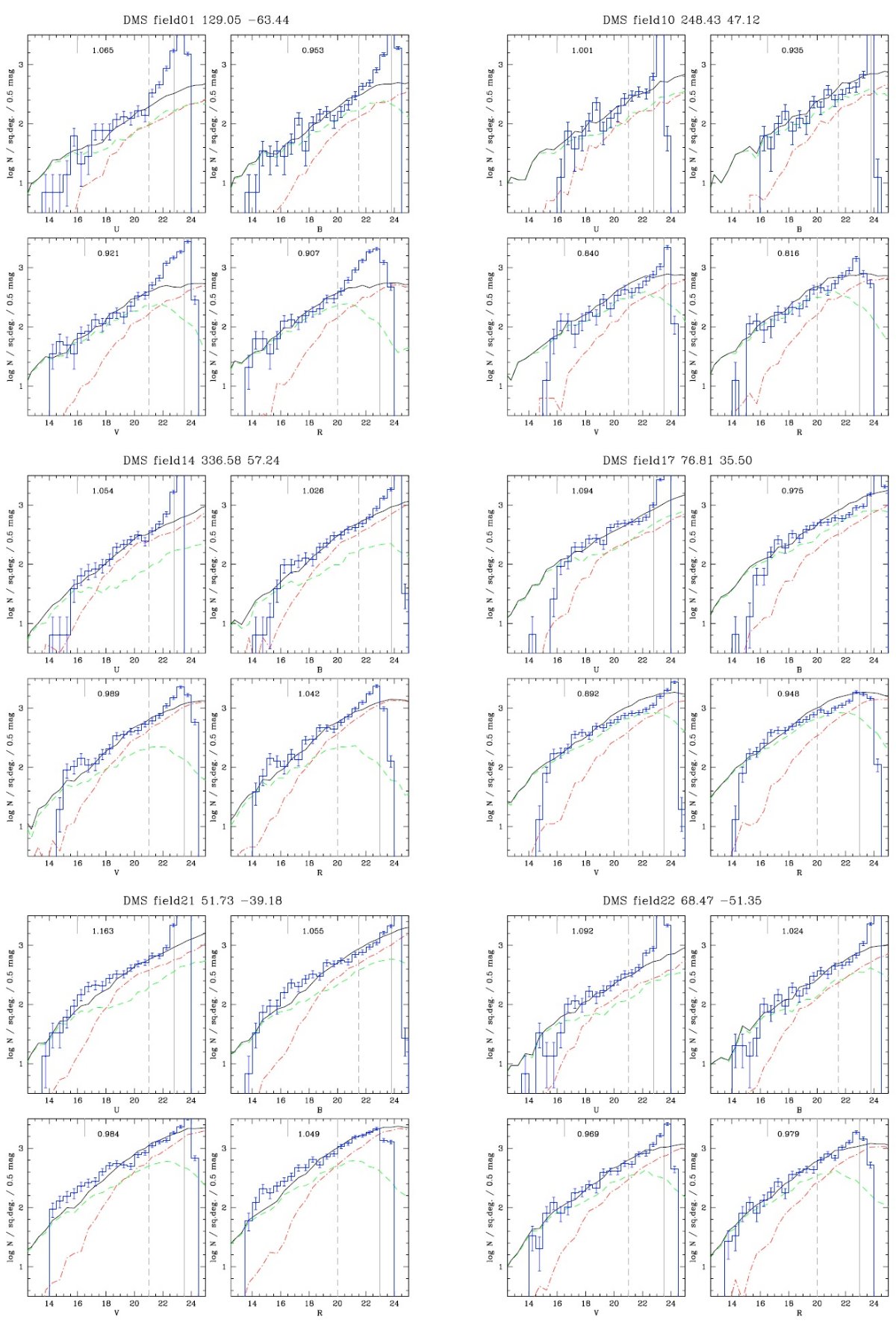
(Mv < 4 の星が二つのスケール高を有する という話でちょっと違う。 ) Mendez, van Altena 1996, 1998 は同じ仮定を使い、さらに後主系列星= 準巨星、巨星、白色矮星には別のスケール高を用いた。これらは以下の理由で正しく ない。 （a）同じ時期に生まれた星集団は初期質量で決まる青や赤の星が含まれる。これらの 青い星と赤い星の空間分布化異なることは考えにくい。 (そうだが、上の研究は色で分けていない。 ) （b）若い星種族は明るい星と同様に暗い星も含んでいる。それらが異なるスケール高を 有するのは不自然である。 （c）星形成銀河では赤色巨星は主に 2 Gyr 以下の若い星である。 Girardi, Salaris 2001 を見よ。巨星に大きなスケール高を付けるのは間違いである。 (あまりピンとこない批判。 ) 第２の方法 第２の方法は過去１０年、Robin, Creze 1986, Haywood, 1994, Ng et al 1995, Castellani et al 2002, Robin et al 2003 などにより進められた。この論文は、EIS = ESO Imaging Survey, 2MASS, SDSS と合うモデルを提供することである。研究目的は （１）異なるバンドを使うサーベイ結果に対応できるようツールを開発する。 （２）異なる測光深さにも対応できる。深い場合は小質量矮星まで計算に含めなければ いけない。 |
２．１．計算スキームTRILEGALコードは C 言語で書かれた。その中核は与えられた質量、年齢、メタル量 の星を恒星進化経路のデータベースから探し出すルーチンである。もう一つは 与えられたバンドでの等級を導くルーチンである。 スキーム 図１にコードのスキームを示す。４つの要素があり、それらは、(a) 進化経路 ライブラリー、(b) 計算スペクトルライブラリー、(c) 観測系のパラメタ―、 (d) 銀河系成分の記述、である。進化経路は等時線の形で、スペクトルは輻射補正 の形で保存されている。 銀河系成分 銀河成分は星の年齢分布(SFR)とメタル分布(AMR), 質量分布(IMF)、 さらに密度分布、星間減光で記述される。 ２．２．シミュレーション出力TRILEGAL では、確率分布に従って星が産み出されるモンテカルロ シミュレーションを行っていた。そこから、シミュレーション測光カタログが 作り出される。 |
 図１．計算コードの構成。実線矢印は主コードでの計算の進行を示し、 最終的には測光データを生み出す。破線矢印はオプションの処理。 |
|
５種類のデータベース TRILEGAL は次の５種類のデータベースを使用する。 １．進化経路テーブル。パラメタ―は 初期質量, 年齢、メタル量。 ２．輻射補正の表。BCλ を Teff, log g, [M/H] の 関数として与える。 ３．初期質量関数 ４．星形成率 ψ(t)、年齢メタル量関係 Z(t) を銀河系成分毎に与える。 ５．銀河系成分の形状、つまり ρ(r)。微分減光 dAv(r)。 ３．１．進化経路我々が集めた進化経路を図２に示す。３．２．輻射補正BCλ ライブラリー(L, Teff, [M/H]) セットから BCλ が決まる。 Mbol = -2.5logL + Mbol,o Mλ = Mbol - BCλ BCλ は合成及び観測スペクトルのデータベースから導かれる。 その方法は Girardi et al 2002 に述べた。 スペクトルライブラリー 大部分の星に対しては Castelli et al 1997 が Kurucz 1993 ATLAS9 コードで 計算した非オーバーシュートモデル大気スペクトルが得られる。これらは Teff = [3500, 50,000]K, [M/H] = [-2.5, 0.5] をカバーする。 Teff > 50,000 K は黒体スペクトル。 M-巨星は Flux et al 1994 の観測スペクトル。 Allard et al 2000 の "BDdusty1999" スペクトルは Teff = [500, 3900] K の矮星をカバーしている。 DA 白色矮星のモデルスペクトルが Finley et al 1997, Homeier et al 1998 から Trff = [5000, 100,000] K で得られる。 Aλ/Av Aλ/Av はスペクトル型と測光システムにも依存する。そこで この値も使用バンド毎に計算した。ただし本論文では G2V 星に対し、 Cardelli et al. 1989 の Rv = 3.1 の場合のみを計算した。 |
 図２．太陽メタル量の進化経路全て。データセットはあと６個のメタル量に対して 同様の進化経路を保存している。データ源毎に色分けした。黒(Girardi et al 2000)＝低中質量星の最も進化の進んだ段階。マゼンタ（Marigo et al 2003) = TP-AGB 期。緑(Bertelli et al 1994) = 大質量星。赤(Chabrier et al 2000) = 非常に低質量な星、褐色矮星。青(Vassiliadeis, Wood 1994) post-AGB, PNe。 |
３．３．初期質量関数 (IMF) φmこの論文の規格化は下のように定めた。∫mφm dm = 1 Mo これは, 星形成率の表式を Mo/yr と表したいからである。この論文では、 Chabrier 2001 の
３．４．星形成率 SFR = ψ(t) と年齢メタル量関係 AMR Z(t)入力ファイルψ と Z(t) は各年齢ごとに、 ψ(Mo/yr), Z, σ(Z) の値が入ったファイルとして入力される。 |
補助的に [M/H] = log(Z/Zo), [Fe/H] = log(Z/Zo) - [α/Fe],
Zo = 0.019 を用いた。α 増強はメタル量により扱いが異なるので注意。
([Fe/H] いいか？ ) AMR Z(t) 古い種族、t ∼ 12 Gyr では 1 Gyr 変化しても光度関数には影響が小さい。 なので星計数には変わりがない。低銀緯や太陽近傍を扱わない限り、星形成率 は銀河系モデルに大きく影響しない。それより重要なのは AMR Z(t) とその 分散である。それは２色図上の位置とカラー分散に大きく効く。 論文１で用いた値 （１）円盤では過去 11 Gyr, ハローでは 12 - 13 Gyr SFR = 一定。 （２）円盤の AMR は Rocha-Pinto et al 2000 から採った。Fuhrmann 1998 データにあるように α 強化は低い [Fe/H] で大きい。この効果 を [Fe/H] からメタル量 Z への変換に取り入れた。どの時期でも [Fe/H] の分散は一定で 1 σ = 0,2 dex である。 （３）ハローでは Z = 0.0095, 1σ = 1.0 dex とした。これは [Fe/H] = -1.6±1.0 (Henry, Worthey 1999) に α 強化を 組み入れたものである。 |
|
固有色等級図が計算できるようになった 恒星進化経路とスペクトルのライブラリーが揃ったので、星形成史、年齢メタル量関係、 初期質量関数を選択すると、固有色等級図を計算することが可能となる。 これは、旧来の観測的色等級図に対応するものである。 円盤とハローの固有色等級図 図３に我々の選択に対応した円盤とハローの Mv - (B-V) 図を示す。図の上辺と右辺 には Mv と (B-V) の分布も示した。この図の特徴は （１）銀河モデルを作る要素として、進化段階が完全に網羅されている。図の明るい 天体に限ると、円盤の若い主系列星、準巨星、巨星、レッドクランプ、水平枝星 が目につく。これらは浅い測光サーベイで観測される星の大部分を占める。 （２）白色矮星、褐色矮星などをモデルに組み込んだので Mv ∼ 44 までの 暗い星を扱えるようになった。これらは非常に深いサーベイでは大量に出現する。 （３）ただし、これらの暗い星は太陽メタルでのみ計算されているため、図３で Mv ∼ 19 付近で主系列が急に細くなっている。 （４）Mv > 6 の矮星では IMF の取り方で大きく影響される。一方その上は SFR, AMR の効果が大きい。 円盤の近赤外固有色等級図 図４に円盤の MK - (J-K) 関係を示す。これは BV 図と大きく異なって 見えるが、 2MASS データの扱い |
 図４．図３と同じだが、円盤の MK - (J-K) 関係に限った。 |
|
薄い円盤 ρd = Cd exp(-R/hR)f(z) (6) 垂直方向分布 f(z) は指数関数型 exp(-|z|/hz) か、 ハイパボリックセカント二乗型 sech2(0.5z/hz) である。 重要なことはスケール高 hz が年齢 t と共に増加することで、 Rana, Basu 1992 によると、 hz = z0(1+t/t0)α (8) これは、星が形成時にはスケール高 z0 で生まれ、その後垂直方向に 拡散していくことを意味する。実際には計算コードは限られた数の年齢間隔にしか 対応できない。全年齢期間は Nd 個の副期間に分けられ、それぞれ の副期間に対して星の密度が計算された。 規格化定数 Cd は、太陽近傍で与えられた総表面密度になるよう に決める。 Σo = ∫0tG ψd(t)dt∫ρd(ro)dz ここに、ψd(t) は太陽円での単位円盤面積当たりの SFR, tG は銀河系年齢である。こうして、円盤形状は、 Σd,0, hR, z0, t0, α で 規定される。Nd を調整して計算時間の効率を上げても良い。 われわれは Nd = 100 を使用している。 厚い円盤 薄い円盤と同様、こちらも二重指数関数での表記と指数関数かける sech2td,0, hR,td, hz,td だけである。言うまでもないが、この成分を式７で t が十分に大きい時 に適当な hz を考えて組み込むことも可能である。 |
ハロー ドボークルー 1959 の r1/4 則を投影 (Young 1976) した形、又は Gilmore 1984 のようなオブレート型回転楕円体も可能である。ハロー密度 ρh のパラメタ―は動径方向スケール rh, 平坦度 bh, それに太陽付近でのハロー星密度、 Ωh,o = ∫otG ψh(t)dt である。 バルジ 計算コードには三軸不等の丸められた楕円体として含まれているが、較正は 行われていない。それでこの論文で示す計算にはバルジ成分は含まなかった。 円盤減光層 ダスト層は指数関数型、スケール高 hz,dust で分布している。 その規格化の第１の方法は近傍での減光密度 Avo = 0.75 mag/kpc (Lynga 1982) を使うか、 Schlegel et al. 1998 の与える無限大までの吸収 Av∞ を採用するかである。我々は そっちを採用した。 hz,dust 110 pc とした。 (第２というのは Lynga のことか？ ) 追加 LMC や星団などを扱う際の追加機能も計算コードに加えた。Marigo 2003 の LMC 計算 などはこの機能を使用した。 |
|
方向 二つのモードが用意されている。一つは (l, b) と領域面積を指定して 星計数を求めるモード。もう一つは太陽を中心に体積限定サンプル をとるものである。 |
等級分解能 もう一つのパラメタ―は等級分解能である。この論文では &Delta:m = 0.1 mag を使用した。 |
４．１．論文１の較正円盤パラメタ―IMF, SFR, AMR は３．３、３．４節で述べた通りである。円盤は二重指数 関数型の単一モデルを使い、薄い円盤、厚い円盤には分けない。その代り、 スケール高は式７で表されるような年齢の関数とした。ただし、Rana, Basu 1992 で得られた z0 = 95 pc, t0 = 0.5 Gyr, α = 2/3 と同じではない。それだと Ng et al 1997 が導いた厚い円盤、古い円盤、 中間円盤、若い円盤を上手く表現しないからである。論文１では、 z0 = 95 pc, t0 = 4.4 Gyr, α = 1.66 が採用 された。 (これは随分大きな変更ではないか？ ) 較正領域 DMS = Deep Multicolor Survey (Osmer et al 1998) 6 領域 EIS = SGP 方向 (Prandoni et al 1999) CDFS = Chandra Deep Field South (Arnouts et al 2001) 上７つでの較正確認 これらのどれもバルジを含んでいなかった。 太陽位置 太陽は銀河面から 15 pc 上にあるとし、銀河中心からの距離 Ro = 8.5 kpc とした。 ハローの扁平率 ハロー星を上の観測で 0 < B-V < 0.7 (20 < B < 22) または 0 < V-I < 0.8 (18 < I < 20) と定義し、 較正７領域でのハロー 星の数をフィットして扁平率 q = 0.65±0.05 を得た。ちなみに Reid, Majewski 1993 は q = 0.8±0.05, Robin et al 2000 は q > 0.6, Cohen et al 2001 は q = 0.55±0.06 を得た。 円盤スケール長 円盤星は 1.3 < B-V < 2.0, 20 < B < 22, 1.8 < V-I < 4.0, 18 < I < 20 で定義した。円盤星のフィットから hR = 2.8±0.25 kpc が得られた。この値は、 Bahcall, Soneira 1984 の hR > 2.5 kpc と合うし、Zheng et al 2001 が M-矮星から得た hR = 2.75±0.16 kpc, Ojha 2001 の hR = 2.8±0.3 kpc とも合う。 ４．２．距離指数の分布図５には NGP 方向での距離指数 μ0 = 5logr - 5 の分布を示す。 円盤星は 1 Gyr 刻みの年齢別(スケール高が変わる)に分布を描いた。 |
 図５．最初の較正時 NGP 方向シミュレイションでの距離指数 μ の分布。 円盤成分の年齢 1 Gyr 刻みの各成分が曲線に付けた数字で示されている。ハロー も同様。上：全曲線。下：若い成分の拡大図。 若い円盤成分は μ = 8 - 12 の比較的近距離でのみ見つかり、一方ハロー成分は μ = 15 をピークとした ガウシャン分布をしている。これは、体積の増加と密度の低下との兼ね合いで 決まる値である。古い円盤星ほど沢山、離れた所に現れている。各年齢群で 分布は緩やかな増加と急激な低下の非対称な形をしている。ハロー星はほぼ ガウシャンの対称分布である。 |
５．１．最近の較正変化時間グループの数論文１では N10 = 10 であったが、現在は N10 = 100 となり、薄い円盤の厚みの増加はほぼ連続的に変化している。 ハロー密度分布 Ryan, Norris 1991 によるメタル量分布を採用した。 太陽位置 太陽の銀河面高度は Maiz-Apellaniz 2001 の 24.2 pc とした。 2MASS と ヒッパルコス 上述の変更は星計数に小さな変更しかもたらさなかった。しかし、 2MASS とヒッパルコスの結果は大きな変化を起こした。それらは、 １． K ∼ 14 付近で不足 2MASS データと比べると K ∼ 14 付近で系統的に数が足りない。不足量は 高銀緯では小さく、 b = 10 でファクター２に達する。これは LF 勾配の低下を 要求する。 ２．古い円盤星を減らす 暗い星の数はハロー星と最も古い円盤成分で決まる。LF 勾配を緩める方法は 古い円盤星の寄与を減らし、総星計数が減る分は円盤の SFR を上げて補うので ある。具体的には薄い円盤の SFR 年齢スケールを 0.8 倍に小さくして、 最も古い円盤星が 9 Gyr でスケール高 hz = 603 pc とした。 |
３．ヒッパルコス星計数 この年齢スケールの変化は CDFS, DMS, 2MASS の星計数と良く合った。しかし ヒッパルコスサンプルの倍の数の星を予言する結果となった。ヒッパルコス サンプルは、図５を見ると分かるが、 t ≤ 2.5 Gyr の比較的若い星から なり、 hz ≤ 150 pc である。ヒッパルコス星と合わせるには exp(-|z|/hz) → 0.25sech2 (0.5z/hz) と変えればよい。 sech2 sech2 型への変更は合理的でもある。指数関数型は横向き 銀河の輝度分布から示唆された。しかし、円盤内側部は通常ダスト減光で 見ることはできない。一方、等温円盤のモデル垂直構造は sech2 型を支持する。勿論年齢と共にスケール高が増加することからも分かるように 銀河円盤は等温ガスではない。 ＳＦＲをいじる 1 - 4 Gyr では SFR が他期の 1.5 倍と考える。こうすると、 Mv - (B-V) 図が変化して、それはヒッパルコスサンプルには影響するが、 2MASS や 可視の深いサーベイには殆ど効かない。すると、 太陽付近の表面密度 太陽付近の表面密度は Σd,o = 59 Mo pc-2 で、Holmberg, Flynn 2004 が力学的に決めた 56±6 Mo pc-2 と合う。 ハロー星の局所密度 ハロー星の局所密度は Ωh, o = 1.5 × 10-4 Mo pc -3 |
|
深い探査の問題点 深い探査での中心課題は銀河と星との分離である。それについては、 Groenewegen et al 2002, Hatziminaoglou et al 2002 を見よ。 ５．２．１．ＣＤＦＳ探査観測ＣＤＦＳ探査は Groenewegen et al 2002 で扱われた。方向は (l, b) = (220.0, -53.9) の比較的きれいな領域である。観測は 0.263 deg2 に対して UBVRI 5-バンド、JK は JK 観測のある 0.0927 deg2 で 行われた。 星と非星の分離は Groenewegen et al 2002 に論じた。 Schlegel et al. 1998 の減光マップによると、この方向は E(B-V) = 0.014, Av = 0.0458 である。 |
モデルとの比較 図６にはモデルとの比較を示した。観測星数/モデル星数の比はバンドに よるが、 0.87 - 1.08 で一致はよい。 特に面白いのが -0.4 ≤ U-B ≤ 1.2 のサンプルについての比較である。 この青いサブサンプルは V ≤ 18 の明るい星は円盤星、V ≥ 20 の暗い星 はハローが支配的である。したがって、このカラー範囲の星をフィットでき れば円盤とハローの正しい相対比を再現できたと確信できるのである。その上、 このサブサンプルからは高温白色矮星、赤い低質量矮星のような進化モデルが まだ怪しい進化段階が除かれている。 そのような比較が図７にある。最も目立つ食い違いは B = 23 でのハロー星の わずかな超過である。これは、星計数に非常に低質量の IMF が効いてくる等級 であるとか、形態分類の境界付近であるとか様々な理由が考えられるところなので 強い結論は出しにくい。 |
|
観測 DMS = Deep Multicolor Survey は UBVR'I75I86 データを |b| > 30 の 6 領域で取得したものである。そのカタログから "galaxy", "noise", "diffuse object", "long object" を落として 残りを解析した。 モデルとの比較 図８は UBVR の結果をモデルと比較した。データとモデルの一致は 非常に良い。 |
青いサブサンプルとの比較 青いサブサンプル、今回は -0.4 ≤ U-B ≤ 0.8、の比較は再び、円盤と ハロー星の相対比率をモデルが正しく定めているかの判定に有用である。図９ を注意して調べると、フィールド 21 ではモデル円盤星が不足していることが 分かる。この領域は DMS フィールドの中では最も内側でモデル較正に最も 問題のある個所である。 |
| EIS 観測は (l, b) = (306.7, -87.9) を中心に 1.21 deg2 の BVI データを撮った。図１０にデータとモデルを比べた。等級分布の 形はよく似ているが、モデルの数が観測の約２倍ある。他の観測との良い 一致を保存して、ここでの不一致を減らす方法はまだ見つからない。 |
 図１０．EIS - deep SGP データ。 滑らかな実曲線＝モデル。赤一点鎖線＝ハローの寄与。緑破線＝円盤の寄与。 |
|
2MASS のありがたみ DMS, SGP, CDFS のように深い探査データはハローと円盤の相対比、ハロー 形状、円板 IMF の研究に理想的であった。円盤の詳細、例えば腕、ダストレーン、 ワープなど、を研究するにはもっと浅いがより広い探査が向いている。 ダストの影響を軽減するには赤外探査が良い。この意味で 2MASS の価値は高い。 サンプル基準 2MASS level 1 science requirement = タイル重なり域から外れていて、S/N > 10, σ < 0.11 低銀緯やバルジの最も込んだ領域を除き、m < 15 なら大体大丈夫。 ２領域のフィットは良好 図１１に (l, b) = (0, 90) と (180, 10) の２領域の例を示した。この２か所 ではフィットは非常に良い。J, H, Ks の星計数図は同じ形なのでこの先は H バンドに限り図示する。 |
反中心から北銀極を通って銀河中心付近まで 図１２には反中心から北銀極を通って銀河中心付近まで、大円に沿って H バンド 計数を図示する。内側銀河面近くではモデルにバルジを入れていないため、 フィットは良くないが、それ以外では概ね満足できるレベルのフィットが 得られた。近銀河中心距離での不一致は貴重である。 2MASS の大部分は円盤星 重要な発見は、バルジから離れた領域全てで 2MASS 星計数の大部分は円盤星で あった。ハローの寄与は殆ど無視できるレベルである。ただし、広範囲での J - (J-Ks) 色等級図には特定の構造、すなわち Marigo et al 2003 が指摘した中央垂直指のようなものもある。つまり、ハロー成分にも 重要な役割がある。 ダスト層の扱い 銀河面に近いと、図１２の最初の枠＝反中心方向が示すように一致は悪い。 不一致の原因の一つはダスト分布が単純すぎることであろう。しかし、その 改善は今回行わない。 |
|
較正サンプル 論文１の較正は V ≥ 15 で行われた。そのような深いサーベイでは、 図５を見ると分かるが、サンプルは円盤では μ = 7 - 14, ハローでは 12 - 18 の星が大部分であった。以前のモデル較正は太陽近傍の星、 すなわち 100 pc 以内、または V ≤ 8 の明るい星、と全く関係なく行われた。 ヒッパルコス ヒッパルコスとタイコカタログは 10 mas 精度の視差を数千の星に与えた。 ヒッパルコスインプットカタログの作成法からは、データからはっきりした 体積制限サンプルを得るための綺麗な基準が作れない。この問題は以前から 指摘されており、ヒッパルコスから太陽近傍でのＳＦＲを得るのに十分な数の 体積制限サンプルを作ることは極度に難しいとされている。 サンプル選択 しかし、我々の目的はそれらの研究とは違う。我々はヒッパルコスから、 完全でシミュレート可能なサブサンプルを考察する。体積制限サンプルには 拘らない。サンプルの選択は以下の事実に基づいて行われた。 （１）ヒッパルコスカタログは V < Vlim = 7 以下の星は全て含む。 （２）上から π > πlim = 10 mas の星を選ぶ。 （３）&pi: のエラーがあるので上で選ばれたサンプルの占める体積は rlim = (1/πlim) = 100 pc 半径の球より少し大きい。 （４）これらの星に含まれる連星は分かっている。 シミュレーションの方法 次に、このサンプルを TRILEGAL コードでシミュレートする。そのために rlim = 200 pc 半径の球内の合成を行う。これならエラーがあっても 選んだ星は全て含まれる。シミュレーションで作られた星の距離 r0 を視差 π0 = 1/r0 に変える。そこにエラー δπ を加え、π =π0 + δπ, r = 1/π が得られる。 このエラーを含んだ距離から得られる「観測的」絶対等級 Mv は次の式である。 Mv = V - 5 log r + 5 シミュレーションの検討１．主系列 図１３にはこのシミュレーションの結果を示す。Vlim = 7, π lim = 10 mas とした。左図は Mv - (B-V) を観測とシミュレーション で較べた。両者の一致は驚くほどである。主系列は Mv = [-4, 9] で幅も位置も 合っている。特に主系列の左側境界がはっきりと一致している。このくっきりした 境界は ZAMS から右側へ動いていく前のゆっくりした進化段階が作り出す 特徴である。 |
主系列の巾は次の二つが効く。 （１）メタル量の分散 （２）M > 1 Mo では対流核オーバーシューティングの効率 観測とシミュレーションの良い一致は、我々のモデルでは上の二つがよく 選ばれていることを示唆する。 シミュレーションの検討２．準巨星と巨星 準巨星と巨星も一致がよい。準巨星と下部 RGB の巾、 RC の位置、RC の上方 で RGB が緩い二本の帯 = (1)コアヘリウム燃焼中間質量星から成る垂直な帯 (2)赤方向に傾く第１RGB と初期 AGB に分かれる様子も正しく再現されている。 星の数 星の数も一致している。観測星数は 4085, モデルが 4182 である。 r, Mv 分布 図１３右図には距離 r とシミュレーションから得た「観測的」Mv の分布を 示す。破線は準巨星と巨星を Mv > 6.82×(B-V) - 2 で定義した 範囲を示す。 r と Mv のずれ r 分布で目立つのは r = 80 pc でシミュレーション星の数が 20 % 超過して いることだ。対応する体積が小さいので、密度分布の非一様性では説明しにくい。 ヒッパルコス視差エラーのシミュレーションがもっと実際に近ければ、この差は 縮まるのではないか。 r = 15 - 35 pc ではシミュレーション星が 20 % 不足している。これも視差エ ラーの扱いが不十分なことに起因すると考える。 一方、 r = 45 pc に見られる観測星のスパイクはヒアデス星団が原因で、 シミュレーションでは考量されていない。 Mv では明るいモデル星が超過し、その分暗いモデル星が不足している。 KS-テストを実施した結果、観測とシミュレーションの二つの Mv 分布が 同じ母集合から実現する可能性は現在のままではゼロ、モデル Mv を 0.26 ずらすと 0.3 まで上がる。しかし、そのように等級をずらす正当な理由は 見当たらない。 ずれの原因は？ 統計の立場からは、上に述べたズレはサンプル数の多さから考えて有意と 見なされる。ズレはモデルの改良点を指し示していると看做すべきだろう。 図１４には少し深いサンプルに対して図１３と同様の図を描いた。 Vlim を深くした結果、 Mv > 2 の星がサンプルに含まれる ようになり、中間年齢から古い星までの寄与が増した。この場合 には星の総数は、観測で 8055, モデルで 7640 である。 |
|
合致度 作ったモデルは、星計数の点では観測と良く合っている。しかし、次の 相違点が問題として残った。 （１）銀河系中心から 30° 以内のモデル星数は観測より不足。 バルジがモデルに含まれていないことは不一致の原因の一つ。しかし、 ハローと円盤のモデルも改良の余地あり。 （２）|b| < 10 の低銀緯帯は円盤モデルの改良とダスト分布、星形成域 の細かい調整が必要。 （３）SGP 方向への予想が観測の半分であった。理由は不明。 最尤解を得るには ここのモデルは最適解を探したものではない。TRILEGAL をいくつかの 銀河系領域の深い探査結果に適用して、最尤解を得ることは原理的には 可能である。しかし、その実施には、 （１）０次近似解（この論文）をまずスタート用に作る。 （２）尤度基準を確立する。 （３）0次から1次へと移るアルゴリズムを開発する。 （４）異なるスタートから同じ解に収束することを確立する。 |
利点 今回分かった TRILEGAL の良いところは、 （１）ほぼ完全な恒星進化経路が用意されている。 （２）広い範囲のスペクトルライブラリー （３）プログラムの変更が容易で、 SFR, AMR, IMF, 幾何形状等を柔軟に いじれる。 （４）他のシミュレーションコードと比べると、異なる進化段階の星 同士の数の比が内部矛盾なく決まる点が特色である。 もう一度 前にも述べたが、 TRILEGAL の利点は入力柔軟さにある。出力も既に １０以上のシステムに対応済みである。 |