2.1.ガラス作成
2.2.特性解析
Fe3+/Fe2+試料の溶融は不活性ガス中では行われなかったので、 Fe2+ イオンの一部は Fe3+ に変わった。Fe3+/Fe2+ 比はガラスの光学性質に影響する。試料をアルゴン雰囲気中でフッ化水素酸に 溶かし、 522 nm 測光から Fe2+ 量を測定する。パイロキシンガラスでは Fe3+/Fe2+ は約 1 であった。オリビンガラスではその比は ほぼ 0.5 であった。
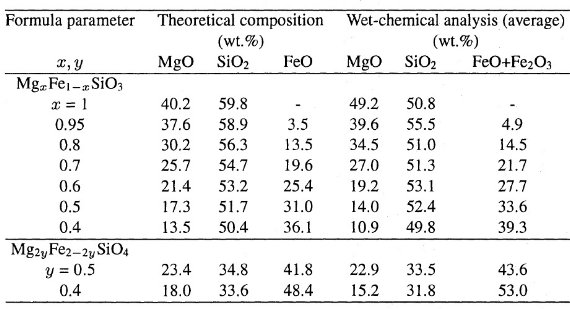
表1.ガラス組成の予想成分と化学分析結果
| MgxFe1-xSiO3 x = 0.4, 0.5, 0.6, 0.7, 0.8, 0.95, 1.0 と Mg2yFe2-2ySiO4 y = 0.4, 0.5 のシリケイトガラスを作った。反射およびエリプソメトリック測定 と透過率測定から 0.19 - 500 μm の光学定数を導いた。 シリケイトダストアナログに関して鉄分の影響が定量的に評価できた。 | オリビンガラスデータを晩期型星の IRAS LRS スペクトルと比較した。 オリビン組成の非晶質シリケイトが晩期型星スペクトルと合うことが示された。 しかし、二つの何度の間の谷間ではシリケイトガラスは透明過ぎ、観測 スペクトルに必要な放射を生み出せない。ダストシェル内側端における シリケイトダスト温度は文献で想定されている温度よりかなり高い可能性が ある。したがって、昔からの疑問=観測から導かれる低い温度とそれより かなり高い凝結温度のズレ、に対し、この新しいデータは差を埋める方向で ある。 |
2.1.ガラス作成2.2.特性解析Fe3+/Fe2+試料の溶融は不活性ガス中では行われなかったので、 Fe2+ イオンの一部は Fe3+ に変わった。Fe3+/Fe2+ 比はガラスの光学性質に影響する。試料をアルゴン雰囲気中でフッ化水素酸に 溶かし、 522 nm 測光から Fe2+ 量を測定する。パイロキシンガラスでは Fe3+/Fe2+ は約 1 であった。オリビンガラスではその比は ほぼ 0.5 であった。 |
 表1.ガラス組成の予想成分と化学分析結果 |
3.1.サンプル形状と埋め込み基質3.2.反射スペクトル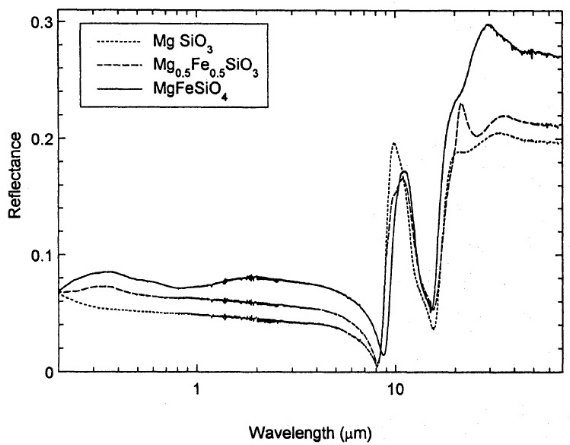 図1.パイロキシンガラス MgSiO3, Mg0.5Fe0.5 SiO3 とオリビンガラス MgFeSiO4 の反射スペクトル。 反射スペクトル 図1に反射スペクトルを示す。10, 18 μm バンドが支配的である。 近赤外では反射率一定だが、可視、紫外には弱い構造がある。その強度は鉄 含有率に相関するので、おそらく鉄の電子遷移に関連するのであろう。 クラマースクロニッヒ 8 - 80 μm ではクラマースクロニッヒ関係式を用いて、m = h + ik を 決定する。これを近赤外・可視・紫外に延長するのは不可能である。と言うのは この関係式は短波長端で吸収がゼロになることを要求するが、我々の スペクトルは電子遷移が残っている波長で終わっていて、そこではまだかなりの 吸収が残っているからである。 振動子フィット この波長域ではローレンツ振動子フィットを3振動子モデルで行う。 電子遷移と振動遷移の中間領域、及び鉄がないサンプルでは反射率は屈折率の 実部で完全に決まる。 |
3.3.透過スペクトル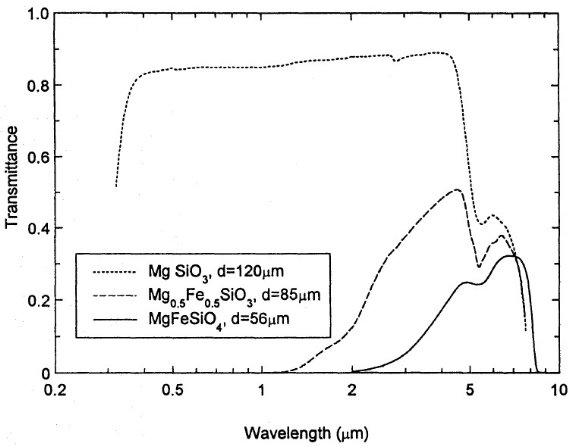 図2.図1と同じガラス薄片の透過スペクトル。パイロキシンガラス MgSiO 3 は 0.4 - 4 μm で透明である。Fe 成分が入る他のサンプル は λ < 2 μm で不透明になる。 反射率補正透過率 T' 図2には図1サンプルの透過率を示す。ここに示される減光は、 反射+吸収+散乱の総計である。反射率 R が分かると、 反射率補正透過率 T' = T/(1-R)2 が分かる。表面散乱の 寄与は分からない。 ランベルト・ビアー則 ランベルト・ビアー則によると、吸収係数 k は下式で与えられる。 k = -ln(T')λ/(4πd) 膜厚 図3には FIR 透過曲線をしめす。長波長側で透過率が上がるのは、 振動遷移の弱まって行くテイルの結果 k が減少するからである。 干渉パターンは厚み d と 屈折率 n の情報を nd の形で含む。 |
|
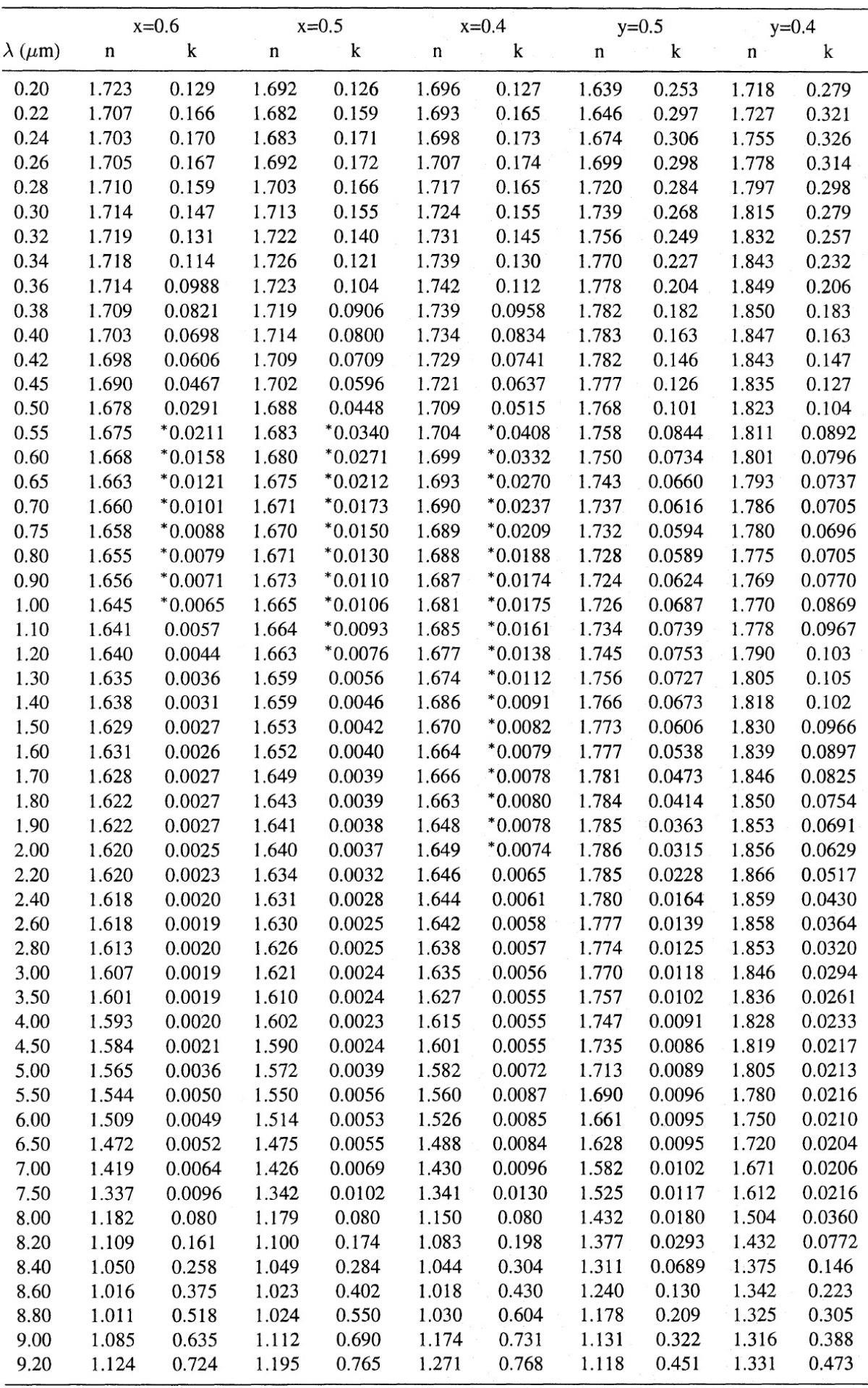
振動子フィット 200 - 300 cm-1 = 33 - 50 μm に共鳴周波数を持つ単一 ローレンツ振動子モデルで透過曲線をフィットした。 厚みdがフィットパラメタ―として決まる。モデルのフィット が良いことから、 k ∝ λ-1 が予想され、これは Q ∝ λ-2 を意味する。 図4、図5= n, k 図4、図5は n, k を示す。短波長では電子遷移が支配的である。そこでは、 酸素イオンの電子による基盤ガラス構造の eigenabsorption とガラスのカラー を決める鉄のような遷移元素の 3d 電子の吸収の二つが効く。鉄の効果は後で 論じる。 Mg, Ca, Sr のようなアルカリ土類元素を含むシリケイトガラスの eigenabsorption は 270 nm 付近に吸収端を持つ。その値は O2+ イオンの結合強度に依存する。非結合酸素濃度が上がると、吸収端波長は長い 方に移行する。図4の鉄を含まないパイロキシンでは、eigenabsorption が n, k の 350 nm から紫外域にかけての増加として現れる。 ( 減光曲線のキンク?) eigenabsorption と振動との間 eigenabsorption と振動との間の波長域では鉄イオンの影響が大きい。 これが図4,5に現れる、鉄分の変化による k の広がりの原因である。鉄成分 が並でも吸光係数はかなりの強さになり、星周空間でシリケイトグレインの熱 収支に重要な働きをする。振動域でも鉄の効果は大きい。表4,5には n, k を示す。 |
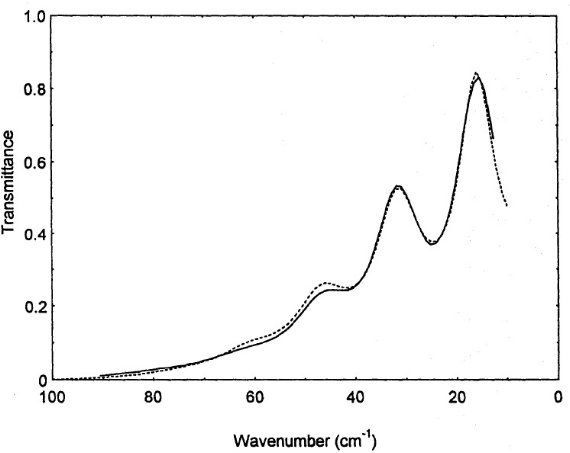 図3.実線=パイロキシンガラス薄膜の FIR 透過率。長波長に向かって 波打ちながら透明になって行く。波は膜内の干渉による。破線=振動子モデル を使ったモデル。 |
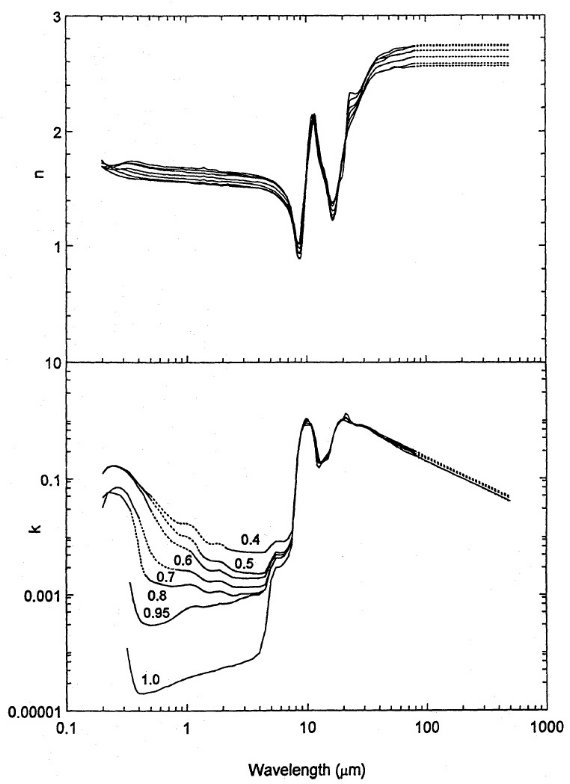 図4.パイロキシンガラスの光学定数。上=n, 下=k. 組成は、MgxFe1-xSiO3. UV/Vis/NIR と FIR で n 曲線は鉄含有量に応じて広がって行く。 k の広がりは巨大である。点線=外挿または内挿。 |
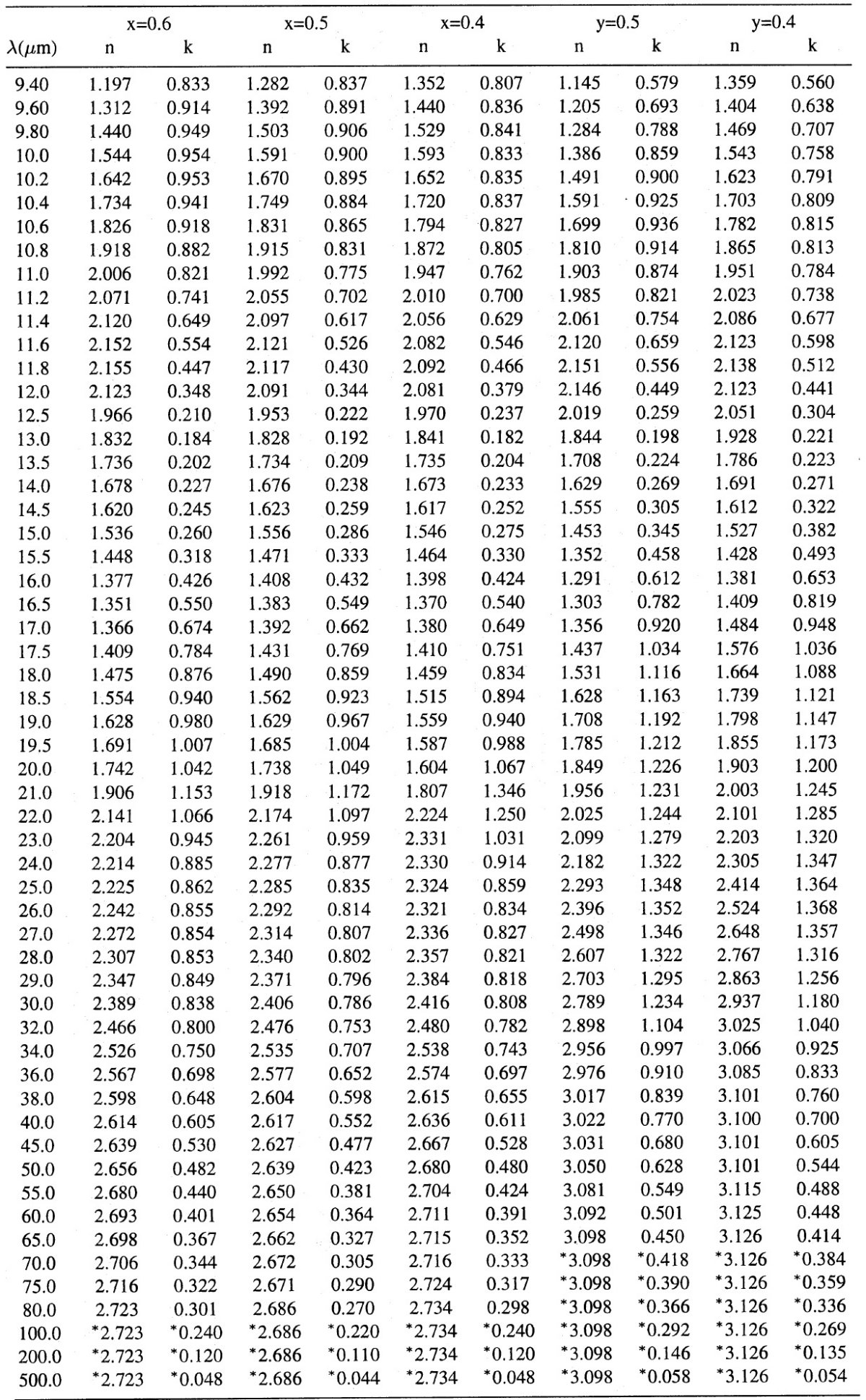
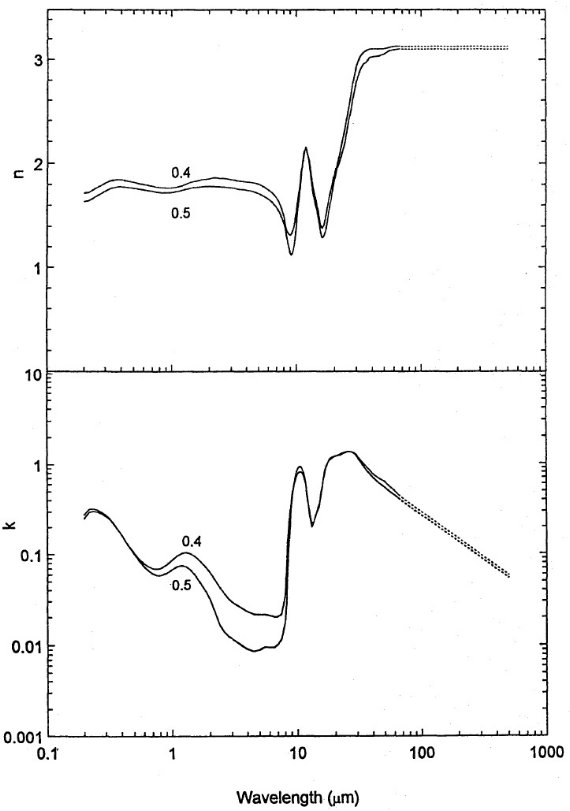 図5.オリビンガラス Mg2yFe2-2ySiO4 y = 0.4 と 0.5. 鉄の影響は図4と同傾向。 |
|
振動スペクトルが単純化 振動ピーク群は鉱物学的な豊富な情報を含んでいる。格子構造が大きく乱れ るとそれらが失われる。当初結晶シリケイトであった物質をガラス化すると、 振動スペクトルが単純化される。オルソパイロキシン(斜方輝石)結晶の 特徴的な多バンド構造は、鉱物が融かされてから急冷されてガラスになると、 ピーク波長 9.5 μm ののっぺりした幅広のバンドに変わる。 Dorschner et al. (1988), Dorschner et al. (1989a,b). 同様に 16 - 30 μm にある入り組んだ バンド群は 18 μm ピークの幅広のバンドとなる。これは格子対称性が 破壊された結果である。この並進対称性の喪失は格子の基本単位の消滅 を意味し、ガラス化するとクリノパイロキシン(単斜パイロキシン)ガラス と区別しにくくなることを説明する。 |
ガラスバンドと結合振動 個々の振動の強度、角度が統計的に揺らぐ結果、全体としてのっぺらした バンドが現れるのであろう。Wang, Angell 1976.SiO4 テトラへド ラの Si-O 伸縮振動 はシリケイトガラスの 10 μm バンドプロファイルに、 Si-O-Si 架橋酸素の 屈伸振動は 20 μm バンドに関わっている。注意すべきはシリケイトグレイ ンと共存する酸化物グレイン中の Mg-O, Fe-O 振動が 20 μm バンドに影響 する点である。Mysen et al 1982, McMillan 1984 はラマン分光に基づき、 個々の振動ピークをガラス構造中の Si-O-Si, O-Si-O, Si-O-Metal の特定の 結合に関連付けた。 ガラス化に残る特徴 しかし、ガラス化を経てなお残る基本的な特徴は存在する。それらは、 ピーク波長、ピーク強度、バンド幅、20/10 バンド比、二つのバンド間の谷間 の深さと巾である。シリケイトの実験的研究から、これらの諸量とガラスパラ メタ―、例えば SiO2 や金属酸化物の含有量、密度などとの間の 関係が分かった。 |
|
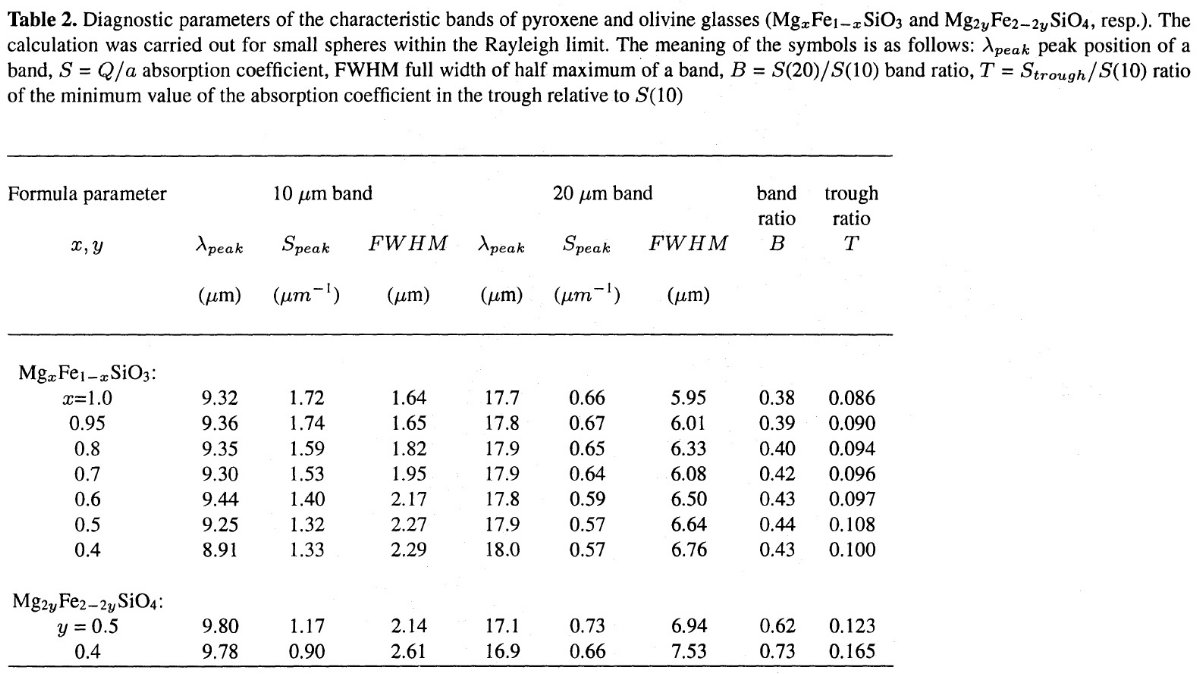
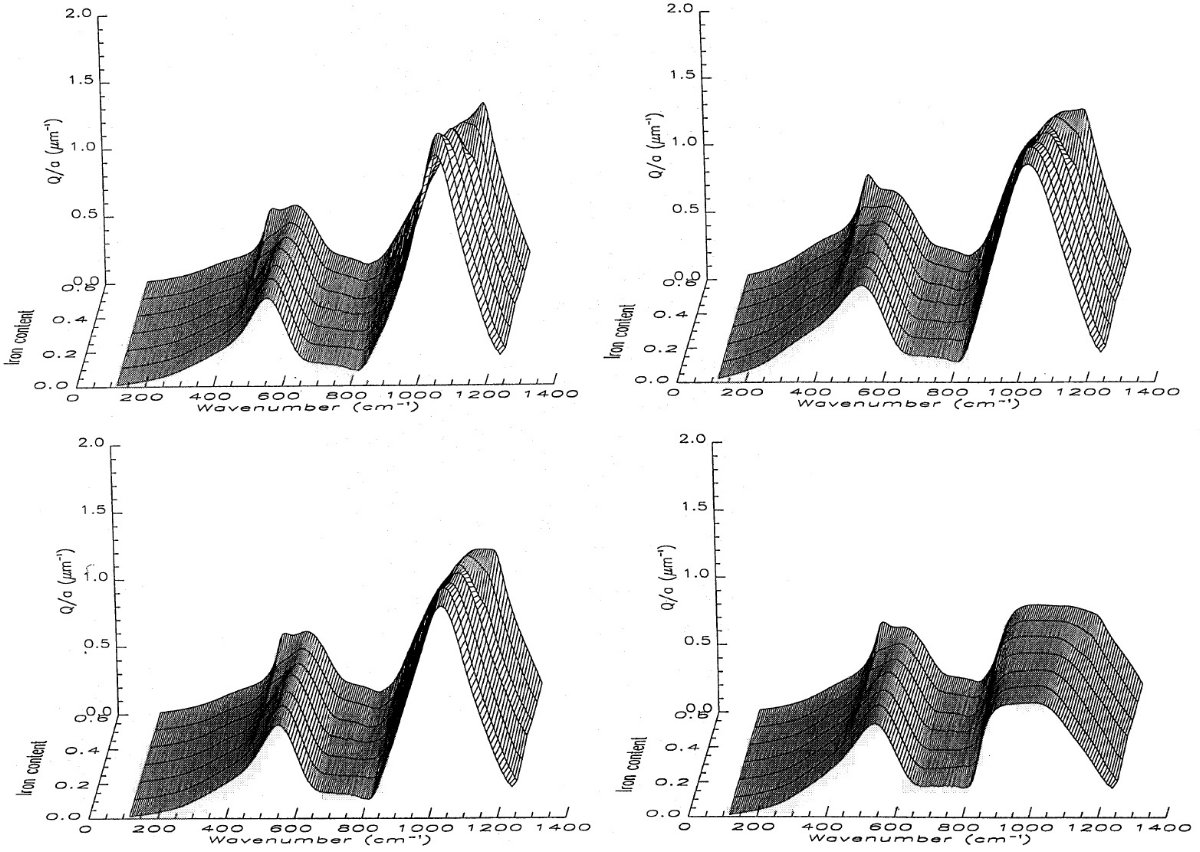
[SiO2], 金属酸化物の量 このような相関に関しては、これまで発表された研究は僅かである。それらは、 Nakamura et al 1984, Koike, Hasegawa (1987), Dorschner 1989 である。Nakamura et al 1984 は SiOx x = 1 - 2 の 10 μm ピーク波長と強度が x の増加と共にずれる。 Koike, Hasegawa (1987), は天然と人造のシリケイトガラスの赤外スペクトルを調べた。彼らは、 [SiO2] 比が増加すると、バンド波長とバンド幅が小さくなることを 見出した。Dorschner et al 1989 はこの傾向をパイロキシンガラスで確認した。 ただし、 Koike, Hasegawa (1987), のサンプルは [SiO2] で 80 % まで、 [Al2O3] で 20 % まで達する高含有量で、宇宙ダストモデルとしては高過ぎる。 また、逆に金属酸化物、 MgO, FeO, Fe2O3 は低すぎる。 しかし、Dorschner ewt al 1989, Jaeger et al. (1994) は宇宙化学の立場から、もっと多くの金属酸化物が含有されるはずと指摘した。 図6=鉄成分の影響 本研究におけるパイロキシン系列の研究は、振動スペクトルへの成分比の影 響を調べる点でユニークである。図6には、球状粒子, CDE = continuous distribution of ellipsoids をレイリー限界で、二種類の半径の球に対して ミー計算の結果を鉄成分比の変化に対する影響として示す。 鉄影響の近似式 表2には、図6のレイリー球粒子のガラススペクトルパラメタ―を示す。 この表を表1の成分比と較べると、データには強い相関があることが判る。 我々のサンプルは [SiO2] が比較的狭い幅に限られるが、鉄 成分の影響が強いという結果が得られた。表3には鉄の影響を一次式で フィットした係数を示す。バンド幅 W(10), W(20), バンド比 B、谷深さ T は鉄含有量と強く相関する。一方、ピーク強度は強い反相関を示す。 しかし、 ピーク波長 λ(10) は鉄量との間にはっきりした関係がない。 λ(20) には弱い相関がある。 |
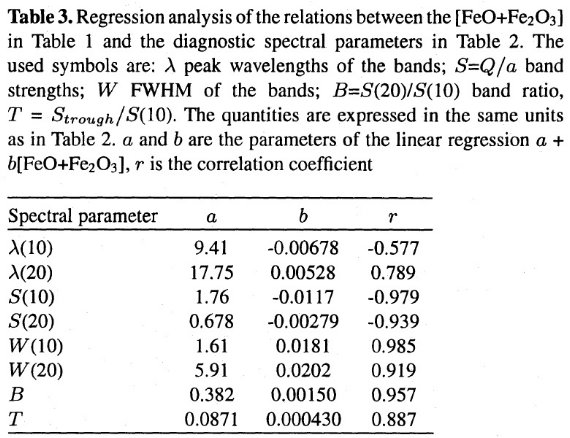 表3.表1の [FeO+Fe2O3] と 表2のスペクトル パラメタ―との関係式 a + b[FeO+Fe2O3] 係数 と r = 相関係数。記号意味は、λ = 波長(μm), S = Q/a バンド強度、W = バンドの WFHM、B = S(20)/S(10) バンド強度比、T = Strough/S(10) 谷深さ. 単位は表2と同じ。 |
|
ガラスの振動帯と固有吸収帯の中間波長域 3.3.節で述べたガラスの振動帯と固有吸収帯の中間波長域では光学定数 は鉄イオンによりひどく影響される。図4,5には、UV/Vis/NIR 波長域にお ける (n, k) が鉄含有量と相関する様子が示されている。鉄分が増加すると、 UV の n は 1.6 以下の値から 1.8 超えまで増加し、構造が現れてくる。 その構造は k の波長依存性によりはっきり現れる。鉄分が最貧の2サンプル では k の精度は低い。今回は散乱ロスを考慮していないからである。 鉄による吸収 しかし他のサンプルは鉄含有量と共に吸収度が強まることを示す。 これは、Burns 1970, Scholze 1988, Bilan et al 1991 なので良く知られて いる広いバンドに起因する。 300 nm 付近の最も強いバンドは電荷輸送偏移 O2- → Fe3+ による。オリビンガラスは 1.1 μm 付近に Fe2+ の 3d-電子準位間の比較的強いバンドを示す。 このバンドは酸素のオクタヘドラル構造による電場の影響で数本に分かれる。 これは結晶場バンドである。対応するパイロキシンのバンドは弱いが、 その代り、 2 μm 付近に乱れたオクタヘドラル配位中の Fe2+ イオンによるバンドが存在する。これらのバンドのプロファイルは完全に 解け合わさっており、近赤外観測でそれらを検出するのは無理だろう。 しかし、これらのバンドのお陰で、適度の鉄含有量で、近赤外連続吸収はかな りのレベルにまで達する。オリビンの 1 μm バンド強度は十分大きく、 観測で検出することも可能である。 ダーティシリケイト このような成分効果が星間、星周ダストに存在するなら、これは星周ダスト の温度に関し重大な効果を及ぼす。地上シリケイト、隕石シリケイト、 これまで作られた実験シリケイトは全て近赤外で吸収が弱すぎて、観測される 星周ダストの温度を説明できない。従って、晩期型星SEDがピークになる 近赤外波長域でシリケイトダストの吸収率を上げる原因を探ることは大きな 問題である。そこで、 Jones, Merrill (1976) は "ダーティシリケイト" を提案した。 Schutte, Tielens (1989) は鉄が宇宙シリケイトで吸収強度を支配すると述べた。 Ossenkopf et al (1992) はシリケイト類似鉱物中の不純物の効果を調べた。 含有された Fe3 O4 が NIR 吸光を強めるのに最も効果的であった。彼らは、 Bedijn 1987, Volk, Kwok 1988, David, Papoular 1990 の相対オパシティ データを使って、二種類の光学データをまとめた。その一つは、 "暖かい低酸素型星周シリケイト" 、もう一つは "冷たい高酸素型星間 シリケイト" と呼ばれた。 図7=光学データの比較 図7にはこの論文で扱う高鉄分ガラス (x = y = 0.5) の光学データを Ossenkopf et al (1992) の高酸素、低酸素型データと比較した。比較のために鉄無しのパイロキシン ガラスと Draine, Lee (1984) のデータも加えた。図を見ると、ガラス中の化学的に結合した鉄が有効媒質 計算で得られた鉄、酸化鉄含有物と同じような効果を有することが判る。 シリケイト 10 μm 帯を有する天体の 2 - 8 μm スペクトル観測が ないので、上述物質のどれが最適かを決めることはできない。 |
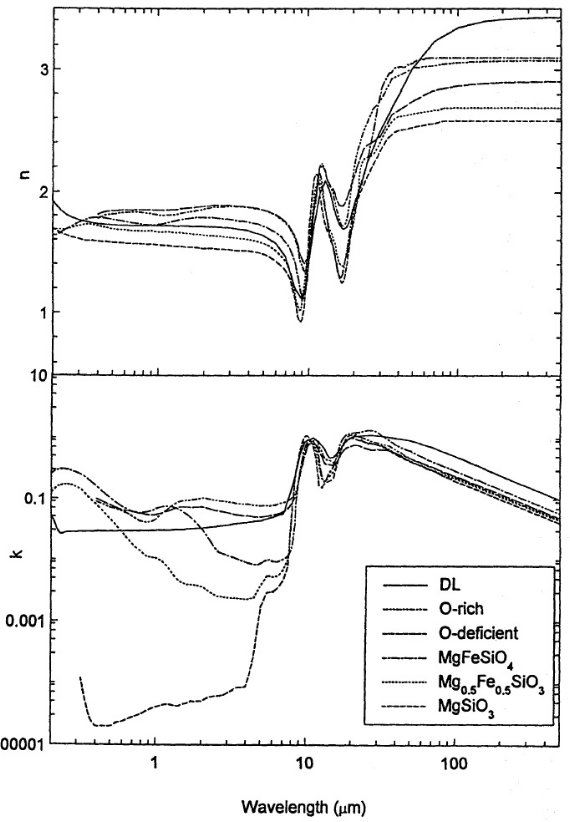 図7.Ossenkopf et al 1990 の酸素欠乏と酸素過多シリケイトの光学定数と Draine, Lee (1984) による x = y = 0.5 の鉄豊富なパイロキシンとオリビンガラスの光学定数の 比較。特に、化学的に結合状態にある鉄が酸化鉄と同じくらいの吸収を生み 出すことを、 k 曲線が示す。比較のため、鉄を含まないパイロキシンガラス も載せた。 |
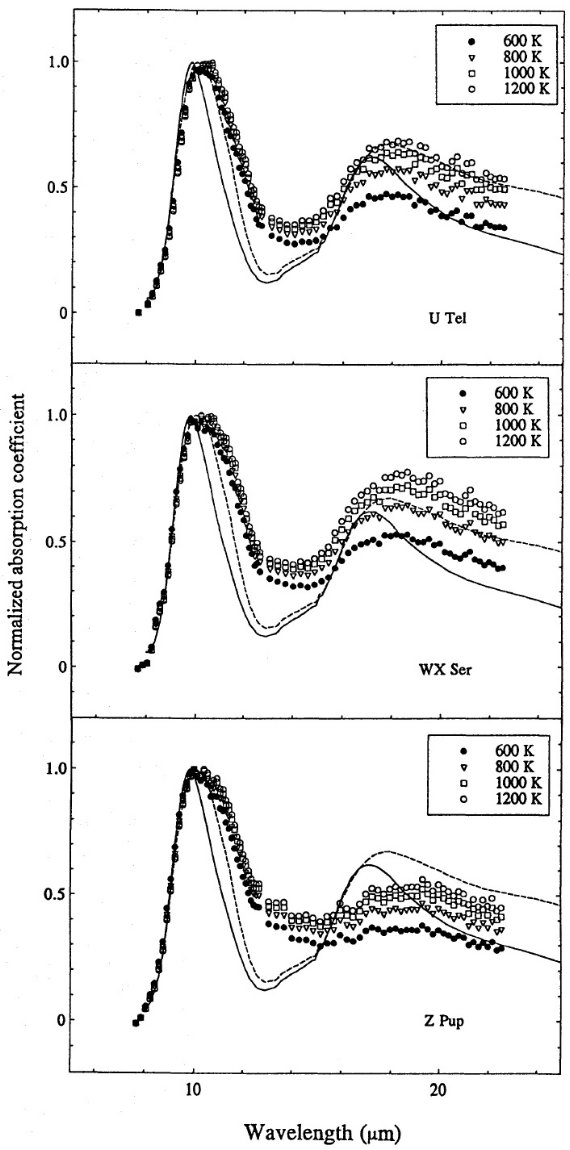 図8.ミラ型星 U Tel, WX Per, Z Pup の光学的に薄い星周ダストシェル での規格化吸光係数。実線=オリビンガラス MgFeSiO4 の レイリー粒子吸光係数。破線= CDE モデル。恒星データはシェル内側半径での 温度により別々のシンボルで示される。 パイロキシンとオリビン Jaeger et al (1994) は Mg と Fe が大体等量のパイロキシンガラスが大質量 YSO や トラペジウム からのシリケイトバンドを上手く再現することを見出した。しかし、 Gurtler, Henning 1986 が示すように、低質量 YSO ではあまり上手く再現できない。 Kompe et al 1994、Sitko et al 1994 は Herbig Ae/Be、 T Tau 星 の LRS スペクトルから、10 μm ピーク波長がシフトすることを見出した。 Mutschke et al 1994 はオリビンの光学定数 (この論文の表5)が観測に より良く合うと述べた。ただし、 LRS のピーク位置には注意が必要である。 Hanner et al 1995 は ρ Oph 暗黒雲中の若い星に観測されるシリケイト バンドはトラペジウムと同じ形で、ピーク波長= 9.7 μm であることを 地上観測から見出した。 星周ダスト吸収係数との比較 Bedijn 1987, Volk, Kwok 1988, David, Papoular 1990 は AGB 星のシリケ イト吸収係数を見出した。観測から、星周層の相対的吸収係数と温度を求める 際の問題は Henning et al 1983 が論じている。Simpson 1991 は質の良い LRS スペクトルのみを用いて、 8 - 22 μm での相対的シリケイト吸収係数を導 いた。彼はバンド比 B = 0.4 というきつい仮定を置いた。これは Draine, Lee (1984) の天体シリケイトから来ている。表2が示すように、この B 値はパイロキシン ガラスに大体等しい。しかし、オリビンの B = 0.6 とは合わない。 Roche 1988 は実際、 GC 方向の星間減光観測から、 B が 0.4 より大きいことを示した。 |
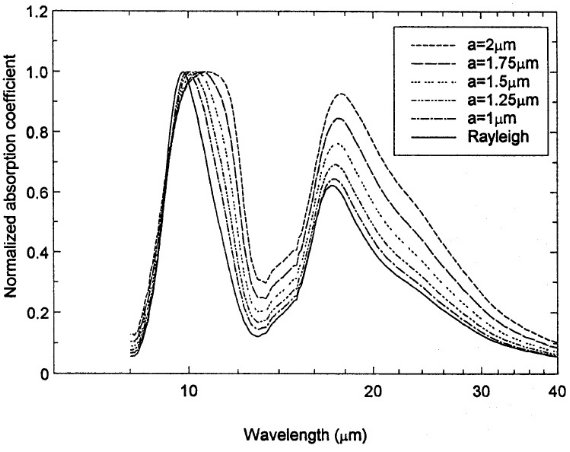 図9.オリビンガラス粒子の規格化吸光係数。ミクロンサイズ粒子では 10 μm 帯の巾が広がり、ピークは長波長側にシフトする。また、 20 μm の強度がまた上がる。 シンプルモデル Simpson 1991 のきつい制限を避けて、 Gurtler 1994 は、光学的に薄い球 対称ダストシェルで、 ρ ∝ r-d, T ∝ r-t という形を仮定し、シェル内側境界温度 Ts をパラメタ―としてモデル計算を 行った。最も単純な場合は d = 2, t = 0.4 である。図8には、殆ど同じ Teff = 2800 K のミラ LRS スペクトルから決めたモデル吸収係数をオリビン レイリー粒子のスペクトルと較べた。吸収係数は Ti = 600, 800, 1000, 1200 K を仮定して計算した。図8には多数の観測の中から代表3例のみを示す。 それらから、 1.10 μm 帯の青側ウィングは良く再現される。 2.グレインモデルをいじれば赤側も再現できそうである。 Henning, Stognienko 1993 はモデルパラメタ―に敏感と述べた。 3.CDE モデルは λ > 15 μm の 20 μm 帯を再現する。 図8の U Tel Ti = 1100 K, WX Ser Ti = 800 K を見よ。 4.谷底の観測吸光係数はオリビンガラスよりずっと大きい。また、谷の 最深点は 14 μm だが、オリビンでは 13 μm である。 5.星毎にプロファイルが変わる。例えば Z Pup の 14 μm より先の 平坦なスペクトルはオリビンでは無理。 6.大きな B は 高い Ti で生じる。オリビンガラスデータを用いることは Simpson 1991 の評価よりダスト温度を上げる。 比較から分かった事 1.オリビンは星周ダスト候補として有望。バンド間の谷が問題。実験室データは 谷が観測より深く、谷底が右上がり。図9で分かるように、サイズを大きくしても 解決に役立たない。 2.サイズを上げると、10 μm バンドの赤い側が上がるので一致が向上する。 しかし、谷底を平らにするには足りない。それに大きなオリビンは 20 μm 帯を上げ過ぎる。 もっとダーティに Mg, Fe のみでは汚さが足りない。Vardya et al 1986 はミラ型星の 12 - 13 μm はアルミナグレインであるとした。γ Al2O3 の Al - O 伸縮振動は 13 μm 付近に来る。これは 尾中ら 1989 が 提案した α Al2O3 の 15 μm に相当する。 星形成における Al の役割は Stencel et al 1990 が調べ、小池ら 1995 は Al2O3 の新しい光学定数を与えた。ゾル・ゲル反応 で作った非晶質アルミナは Begemann 1995 によるとシリケイトの二つのバンド の間を丁度埋める。 最近 Nittler et al 1994 は隕石中にアルミナ粒子を発見 し星周起源とした。その他に、構造の乱れにより Si-O テトラへドラが不完全 で、そのためにテトラへドラに属しない Mg-O, Fe-O 振動が 20 μm 帯の巾 を広げ、同時に屈伸振動強度を弱めるかも知れない。 磨り潰し工程の影響? それに関し、磨り潰して作った粒子のから導いた光学定数は、バルク物質の 反射率測定から導いた光学定数よりも、高い吸収率になることは興味深い。 磨り潰す過程で混じる不純物、または非晶質化の進行など、星周空間では 実験室よりダーティなシリケイトの可能性がある。 |
|
オリビンとパイロキシンの光学定数 シリケイトガラスの二つの系列で、オリビンとパイロキシンの Mg-Fe シリケ イトガラスの全組成域をカバーした。それらの光学定数を求めた。 鉄の量との相関 10, 20 μm バンドの巾、両者の強度比、両バンド間の谷の深さが Fe 量 と相関することが判った。ただし、 10 μm 帯ピークの波長は Fe 量との相関がはっきりしない。 |
3d 電子遷移 Fe2+ イオンの 3d 電子遷移が NIR 吸収に効きそうである。 オリビン オリビンガラスは星周シリケイトとして有望。 |