Optical Properties of Glassy Bronzite and the Interstellar Silicate Bands

　アブストラクト　

　２．ブロンザイトガラスの光学定数　

　２．１．ミクロン以下の粒子の吸光係数から n, k を導く　

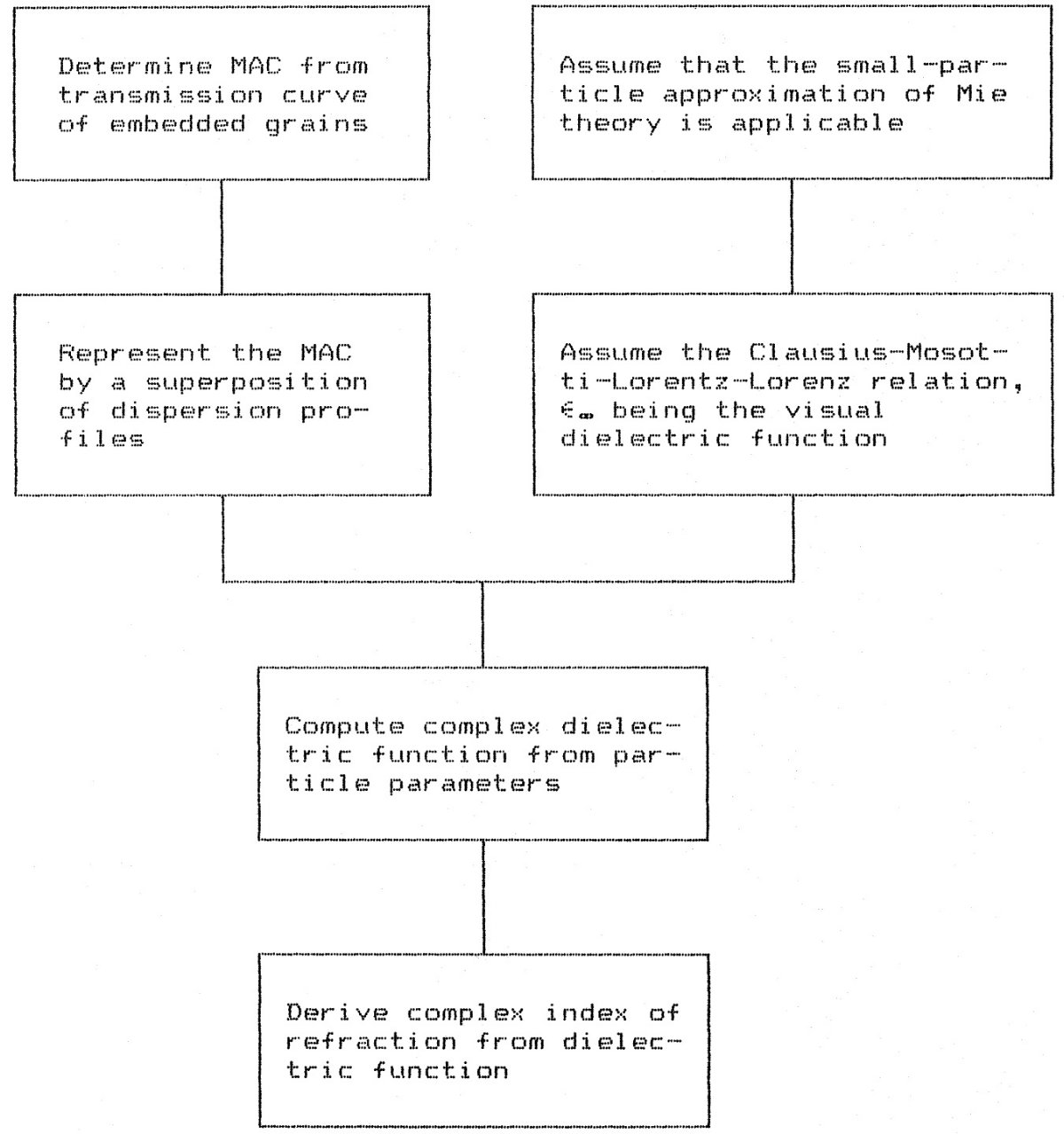
基礎式　 κ = MAC(mass absorption coefficient) δ = 物質密度 a = 粒子半径 Qabs = 吸光の効率 ε = ε' + iε" = 複素誘電率 m = n + ik = 複素屈折率 とする。 　　　κ = (3/4)(Qabs/aδ)　　(1) x = 2πa/λ << 1 の時には、 　　　Qabs = 4x Im[(ε-1)/(ε+2)]　　　(2) 　　　n = {[(ε'2+ε"2)1/2 + ε']/2}1/2　　　(3a) 　　　k = {[(ε'2+ε"2)1/2 - ε']/2}1/2　　　(3a) 　分散式　 　κから　n, k を導くには追加情報が必要である。 クラウジウス・モソッティ・ローレンツ・ローレンツの関係式によると、Ｎ個 の振動子が吸収に寄与する時に、次の関係式が成立する。

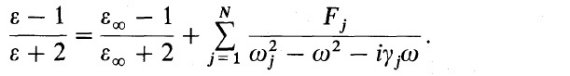ここに、 ε∞ = 高振動数での誘電率。 ω = 角振動数 ωj = j-番目振動子の固有角振動数 &gammma;j = j-番目振動子の減衰定数 係数 Fj はプラズマ振動数 ωp,j と 振動子強度 fj との間に次の関係がある。 Fj = ωp,j2fj/3 こうして、もし Fj, ωj, &gammma;j, ε∞ が判れば、 n, k が計算できる。 式 (1), (2), (4) を組み合わせて、 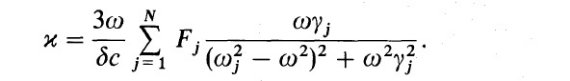が得られる。式(6) を見ると、測定される κ(λ) に式(6) をフィ ットして、 Fj, ωj, &gammma;jを 決めれば、ε が決められることが判る。この方法を図１に示す。

　２．２．ローレンツ型プロファイルによる透過率曲線のフィット　

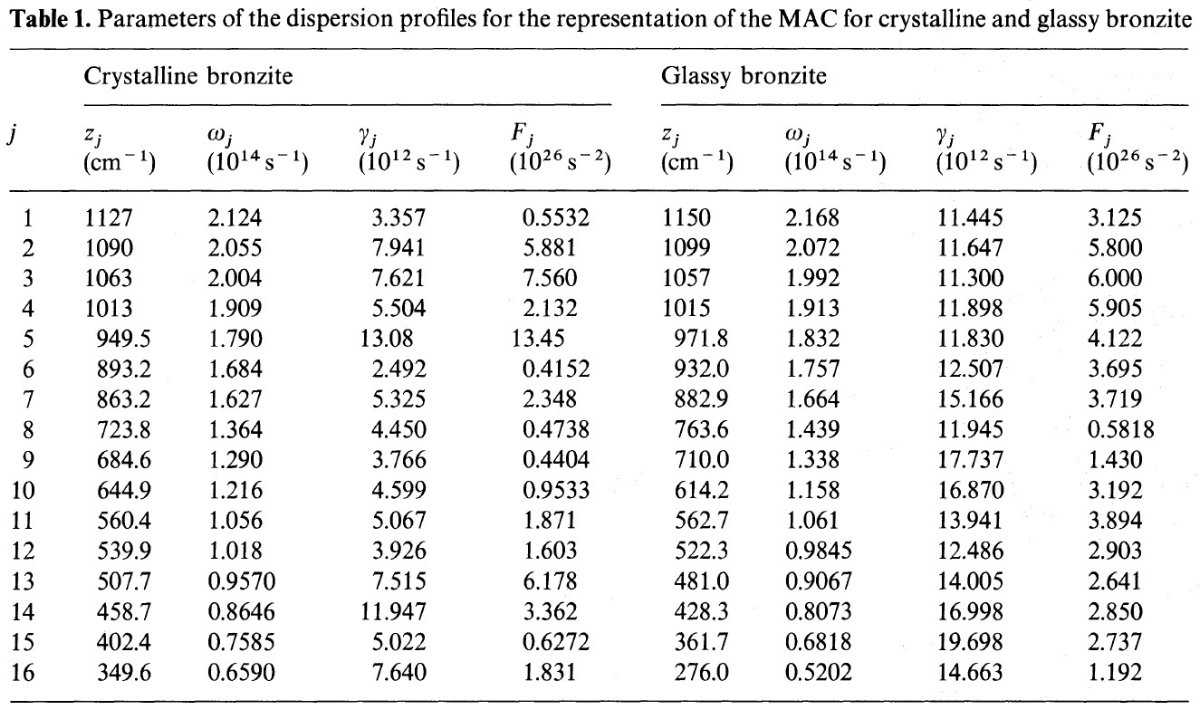
ブロンザイトの透過曲線　 　図２は結晶及びガラスブロンザイトの透過曲線である。結晶の方には少なく とも 12　個の吸収ピークが 7 - 40 μm 区間に存在する。ガラスの方には 複雑な構造は消え去り、二つの幅広な吸収帯が残される。 　振動子モデル　 　MAC = 質量吸収係数は透過曲線から得られる。図３a には 16 振動子でフィ ットした結果を示す。そのパラメタ―は表１に示す。図３b にはガラスブロン ザイトのフィットを示す。ガラスの方には二つの幅広の吸収帯が見えるだけだ が、その形が非対称なので二つの振動子では十分にフィットできない。そこで、 結晶の記述に用いた 16 振動子を基にガラスの方も 16 個の振動子でフィット した。 　ガラスと結晶の比較　 （１）　双方のピーク波長は 5 % 精度で一致する。ガラスの 20 μm 群ピー クは長波長へ、 10 μm ピークは短波長へずれる。 （２）　ガラスのピーク巾は 1.5 - 5 倍広くなる。 （３）　振動子強度 Fj はガラスの方が大きい。

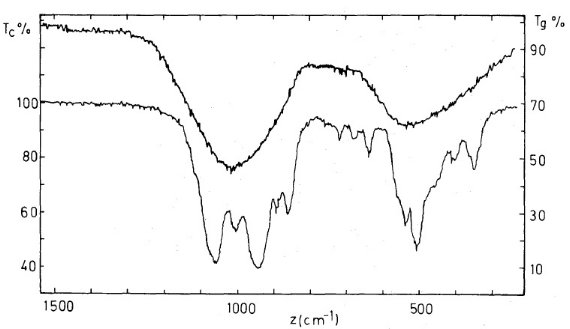図２．Tc=結晶ブロンザイトの透過率。Tg=ガラスブロンザイトの透過率。 KBr 円盤内のサブミクロンサイズ粒子の柱密度＝ 1.59 10-4 g cm-2.

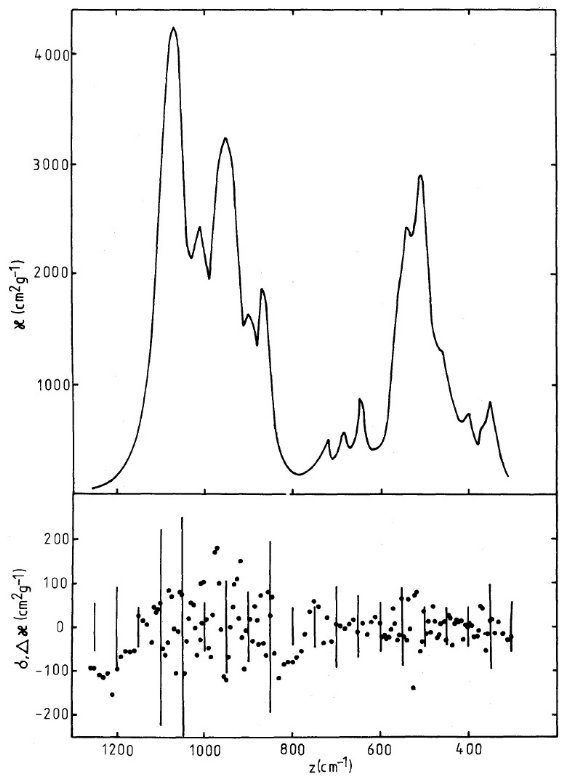図３a．上＝結晶ブロンザイトの質量当たり吸収係数 κ(z).KBr の影響を 補正した透過曲線は 16 個のローレンツ型振動子の重ね合わせで表現される。 下：黒点＝Δκ = 測定ＭＡＣ−モデルＭＡＣ。縦棒＝測定誤差。

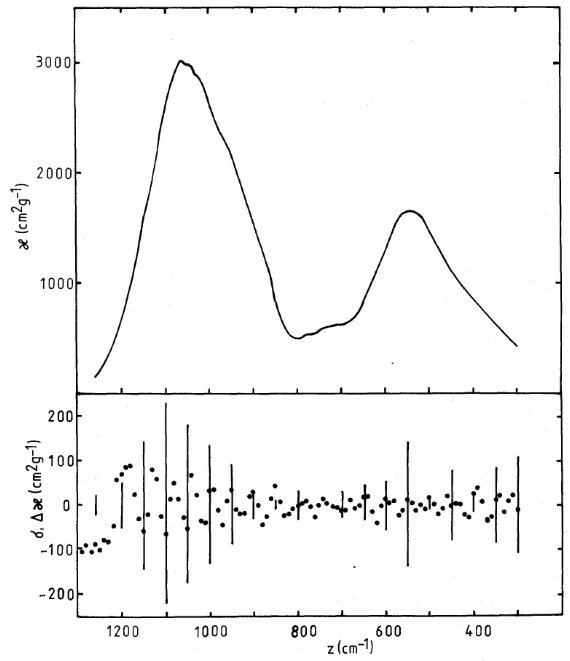図３b．上＝ガラスブロンザイトの質量当たり吸収係数 κ(z).KBr の影響 を補正した透過曲線は 16 個のローレンツ型振動子の重ね合わせで表現される。 下：黒点＝Δκ = 測定ＭＡＣ−モデルＭＡＣ。縦棒＝測定誤差。

　２．３．光学定数 n, k　

　４．議論　

　４．１．ガラスブロンザイトの性質　

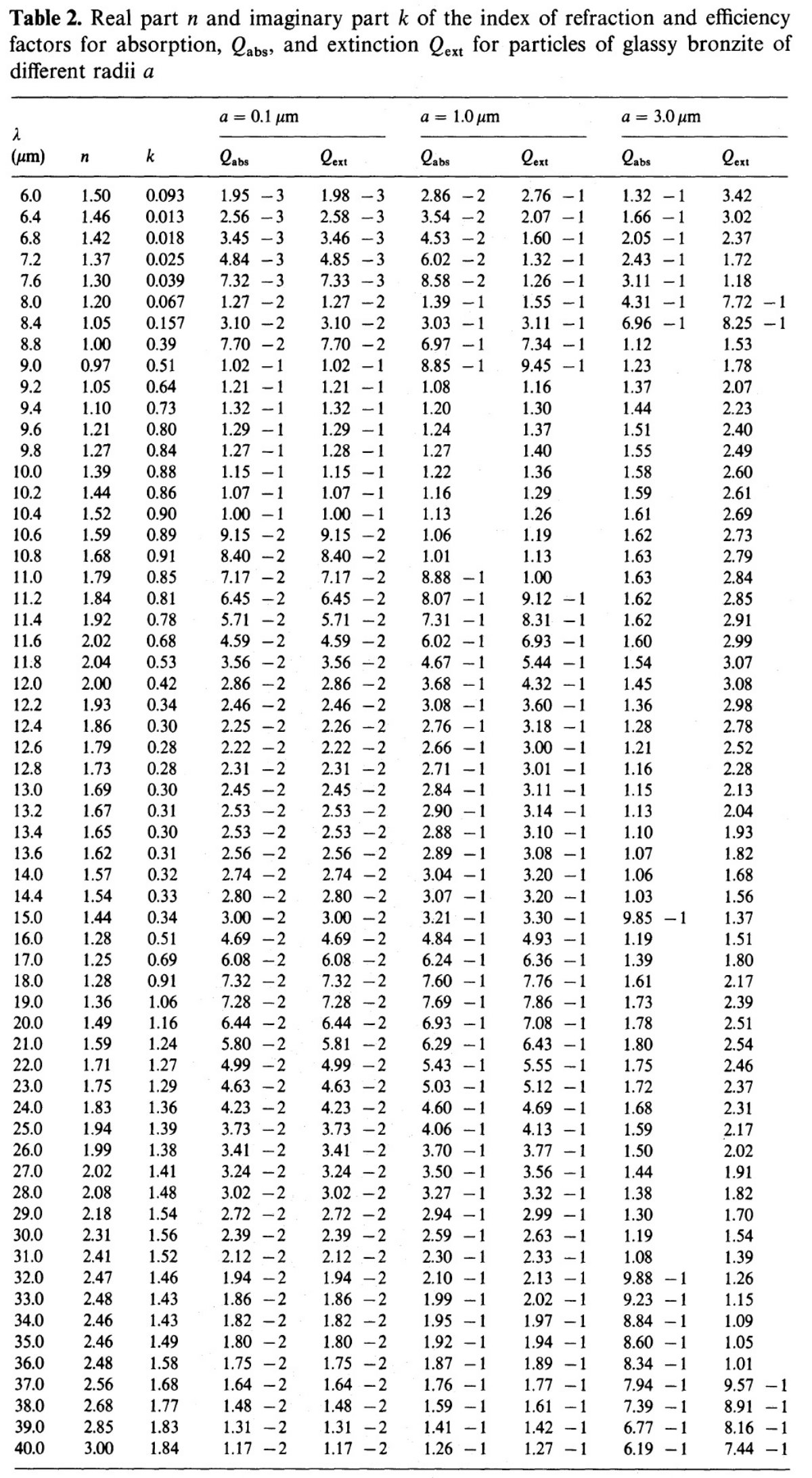
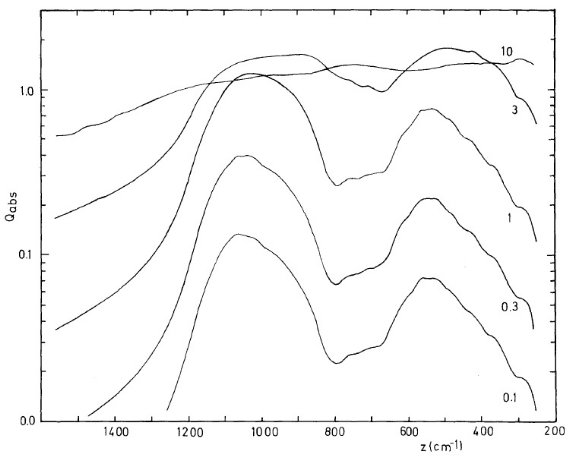図４．ガラスブロンザイトの吸光効率 Qabs(z)。曲線の 数字は粒子半径 (μm) 　Q と a　 　図４には、λ 7 - 40 μm におけるガラスブロンザイトの吸光効率 Qabs(z) を粒径 a = 0.1, 0.3, 1, 3, 10 μm に対して示す。 表３には、10, 20 μm 帯の特性がガラスブロンザイトの粒子半径 a でどう 変わるかをまとめた。a ≤ 0.3 μm では Q は a に依存しない。 　他の実験シリケイトとの比較　 　図５には、他の実験シリケイトとの比較を示す。表４にはそれらをまとめた。 どうも二つのクループがあるらしい。X2SiO4 シリケイトはピークが 9.9 μm, XSiO3 は明らかにそれより 短波長側にピークがある。 10 μm ピーク巾に関しては、ガラスブロンザイ トが最も大きい。もっとも狭いのは照射シリケイトである。20 μm 帯の 性質には組成効果が見られない。照射オリビンはピーク波長最短でかつ巾が 狭い。 　ピーク間の谷　 　谷はブロンザイトとオリビンスモークで浅い。

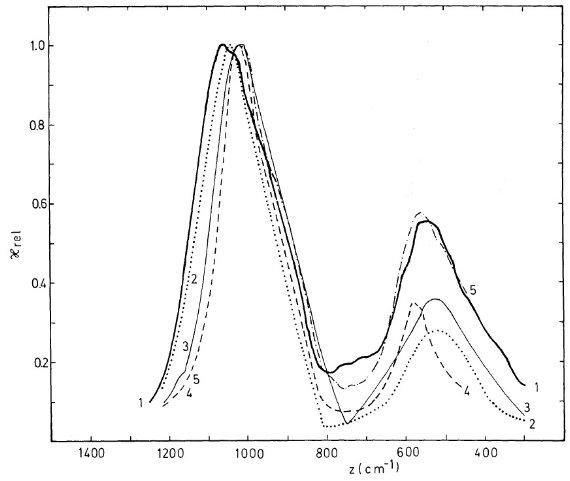図５．10 μm バンドピークで規格化した非晶質シリケイトの MAC の比較。 1=ガラスブロンザイト。この研究。2=非晶 MgSiO3 Day 1979. 3= 非晶 Mg2SiO4 Day 1979. 4=照射オリビン Kratchmer, Huffman 1979. 5=オリビンスモーク。Kratchmer, Huffman 1979. 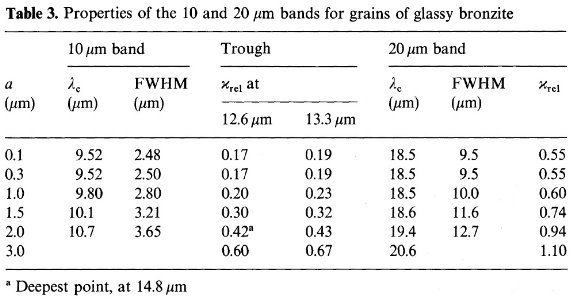表３．ガラスブロンザイト粒子の 10, 20 μm バンド

　３．２．観測との対比　

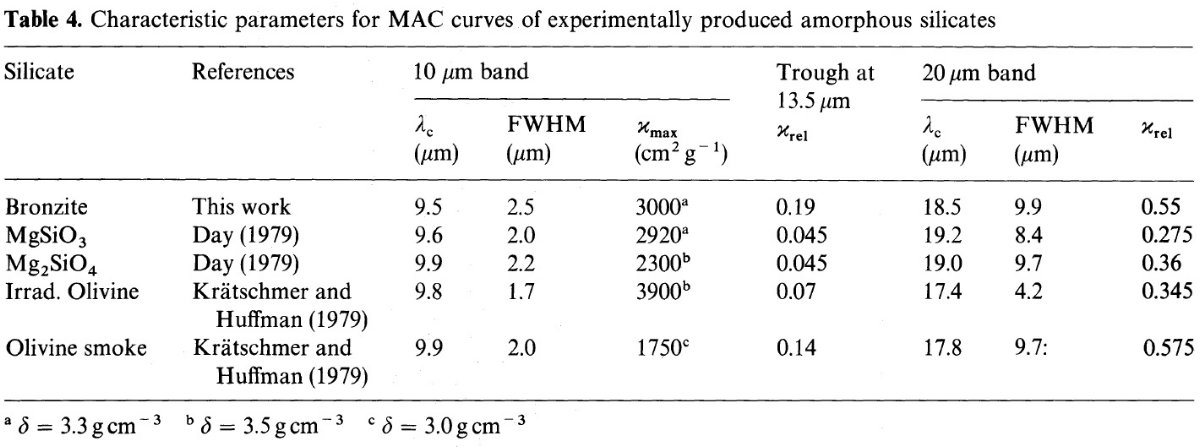
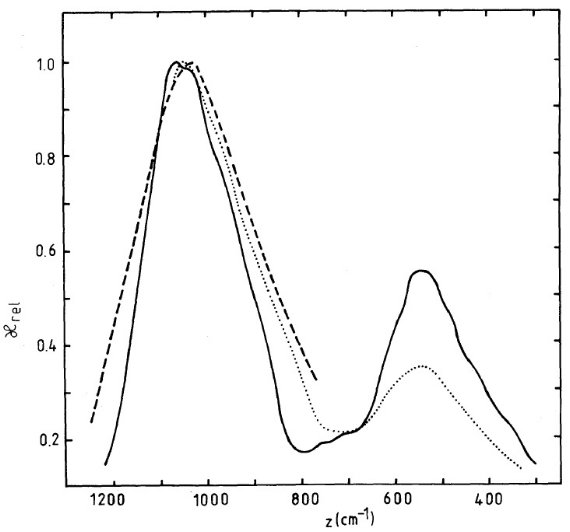図６a．ガラスブロンザイトと観測の比較。実線=半径 a 0.1 μm. 破線＝トラペジウム。点線= "astronomical silicate" Draine, Lee (1984) 　２種類の 10 μm 帯　 （１）若い天体　 　　　T Tau 星, BN 天体, Ney-Allen 星雲 = 9.5 - 9.7 μm ピーク （２）進化した星 　　　酸素過多晩期型巨星。9.9 - 10.0 μm ピーク その違いを説明するために、 Gurtler, Henning (1986) は O-型 = X2SiO4 と P-型 = XSiO3 の二種類シリケイトが存在すると考えた。 　若い天体　 トラペジウム：Td 250 K を仮定して、10 μm バンドの放射率の形。 Rowan-Robinson 1975 はバンド幅が広い 3.5 μm のは粒径が大きい ためとした。仮にブロンザイトの n, k で計算すると半径 1 μm を 越える必要がある。その場合、ピーク位置が 9.9 - 10.0 μm に 移るので観測と合わない。だから、サイズ以外の説明が要る。 T Tau 星。：適当なモデルが無いので吸収係数は出ていない。バンドプロ ファイルの平均 Cohen 1980 ピーク位置はトラペジウムと似る。巾は狭い。 NGC 7538(E)：Chini et al 1986 はこの天体の観測から n, k を出した。 図６b にその n, k から計算した吸光係数を示す。 　astronomical silicate　 　 Draine, Lee (1984) では、10 μm バンドの位置と巾をトラペジウムに合わせ、 20 μm バンドの位置と巾を晩期型星に合わせた。吸収強度比は GC の 観測に合う 0.4 とした。この値は偶々、ブロンザイトガラスおよび Day の 非晶質パイロキシンと一致する。 　晩期型星　 　Henning et al. 1983 と Pegourie, Papoular 1985 は光学的に薄い ダストシェルを持つ晩期型星の中間赤外スペクトルから吸光効率を 導いた。 　ピーク比　 　10 μm/20μm はダスト温度の決定に重要である。その際に 用いられる Q(10)/Q(20) は 0.3 - 0.5 あたり？

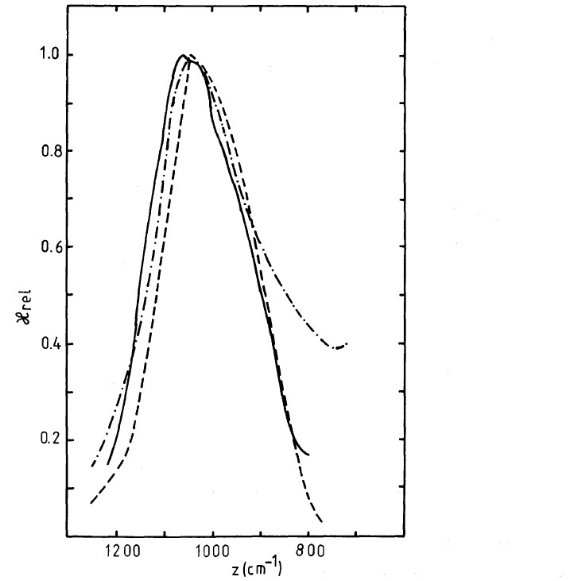図６b．ガラスブロンザイトと観測の比較。実線=半径 a 0.1 μm. 破線＝T Tau 星の平均 Cohen1980。一点鎖線= NGC 7538(E) Chini et al 1986. 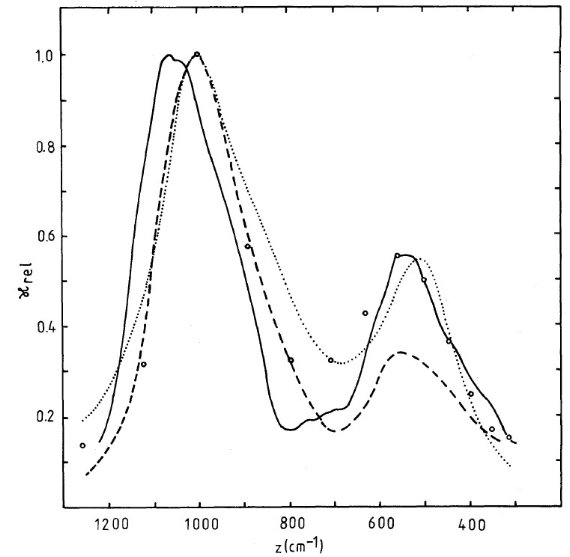図７．実線＝ガラスブロンザイト粒子 a = 0.1 μm の規格化吸光率。 破線＝晩期型巨星、超巨星の吸光率。Pegourie, Papoular 1985. 点線＝Henning et al 1983. 丸＝ Rowan-Robinson 1986.