Theoretical Studies of the Infrared Emission from Circumstellar Dust Shells: The Infrared Characteristics of Circumstellar Silicates and the Mass-Loss Rate of Oxygen-Rich Late Type Giants

　アブストラクト　

　１．イントロダクション　

　２．星周ダストシェルの特徴　

　２．１．外層部の構造　

　２．２．光学的に薄いシェル　

熱平衡ダスト温度　 　この論文の目的は、ミラや OH/IR 星からのスペクトルを解析して、星周空 間で形成されたダストの光学的性質を導くことである。それにはダストの温度 勾配を知る必要がある。そこで、第１歩として光学的に薄い場合を考察する。 星から Teff 黒体放射を浴びるダストの温度を Td とする。Qabs = Teff の プランク関数で平均したダスト吸収効率。Qem = Td のプランク関数で平均した ダスト吸収効率。c = 定数として、 　　　Td(r) = c[(Qabs/Qem)(r*/r)1/2Teff Qabs(λ) ∝ λ-n と仮定すると、Td ∝ r -2/(4+n) となる。シリケイトは λ = 10, 20 νm に 強い吸収帯を持つが、 Td < 200 K ではそれらは励起されないので、 n = 1 - 2 である。 (Qabs の温度依存性の話か、放射の際のプランク関数との 積分で 10 - 20 μm 部分が効かないことをこう表現しているのか？ ) Td = 200 - 1000 K では、放射は λ = 10, 20 νm バンドが支配的となるので、 n = 0 が妥当である。 (プランク関数との積分の話だったらしい。 ) 　ダスト温度の距離依存性　 　一般にはシェル内側境界 r0 において、ダストはその昇華温度 Ts (シリケイトの場合 1000 K)で形成される。光学的に薄いシェルではダスト温度の 分布は、 　　　Td(r) = Ts (r0/r)2/(4+n)　　　　　(2) 内側の Td > 200 K の領域では n = 0 に近く、温度変化は r-1/2 に近い。外側では n = 1 - 2 となるので、勾配が緩くなる。星周ダストからの放射 モデルでは、フリーパラメタ―として、r0 でなく Qabs/Qem を選ぶ。 この値が決まると与えられた光度 L と昇華温度 Ts に対し、エネルギーバランスの 式 (1) から r0 が決まる。 　光学的に薄いシェルからの放出光　 　光学的に薄いシェルからの放出光スペクトルは 　　　L(λ) = ∫4πr2nd(r)4π a2Q(λ)πB(λ,Td)dr　　(3) 一定速度 v の球対称質量放出を仮定すると、距離 D でのフラックスは、 　　　F(λ) = 4π(r0/D)2Ndπa2 Q(λ)∫B[λ,Td(x)]dx　　(4) ここに、 Nd = コラム密度、x = r/r0 である。積分は x = [1, r1/r0] で行われる。近赤外、中間赤外のフラックスを 求める場合、実際には x = [1. ∞] で計算しても結果は変わらない。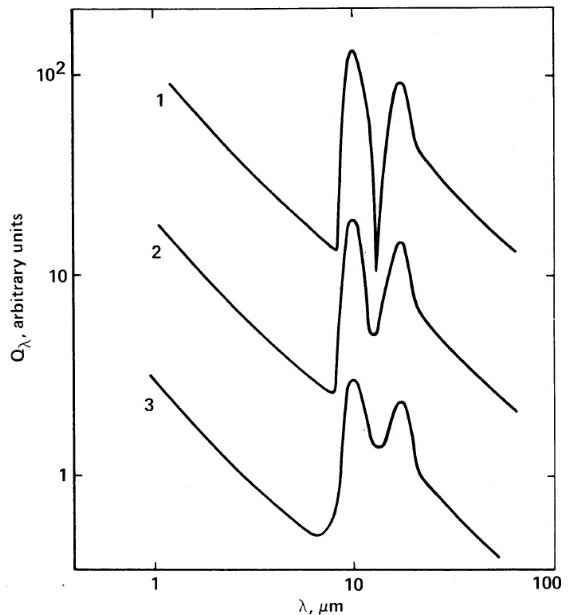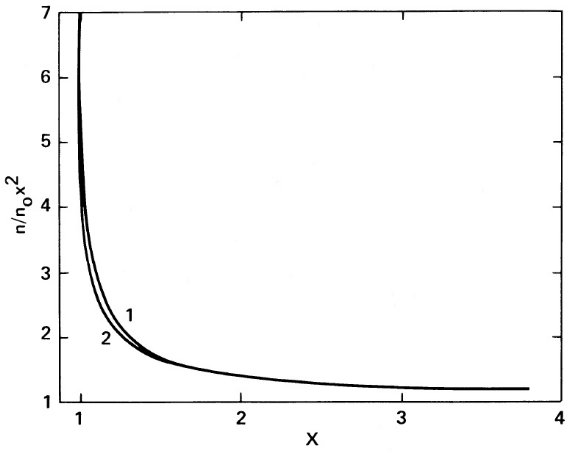 式 (4) は変形すると、 　　　F(λ) = 3(dMd/dt)/(4vρs)[Q(λ)/a] (r0/D)2∫B[λ,Td(x)]dx　　(5) ここに、ρs = ダスト物質の比重。レイリー限界内 (2πa/ λ) ≤ 0.5) では Q/a はグレインサイズに依らない。積分は式 (2) を用いて、数値的に行われる。図１には、積分の値 [∝F(λ)/ Q(λ)] を二つの昇華温度 Ts = 1000 K と 750 K に対して、n = 0 の場合の積分を示す。

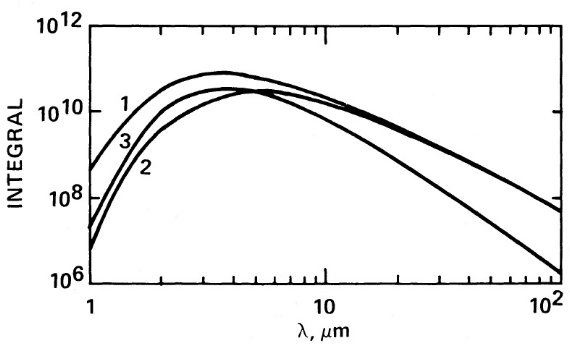
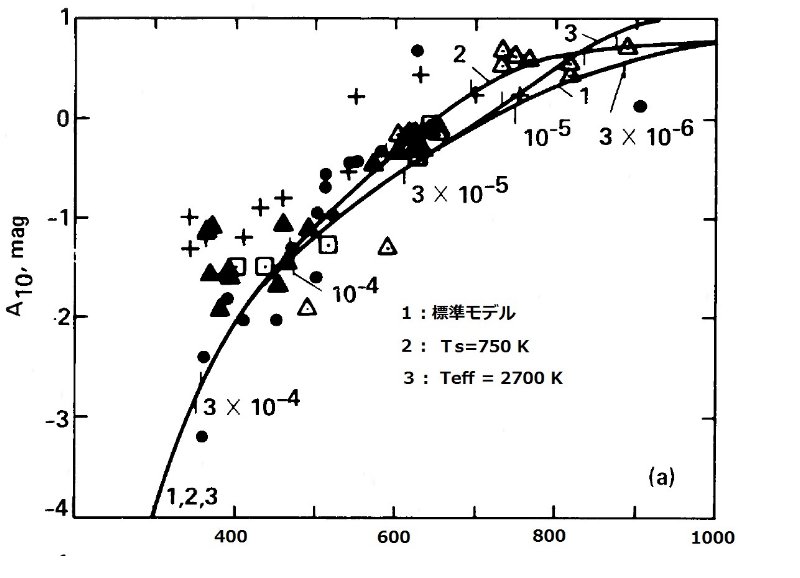
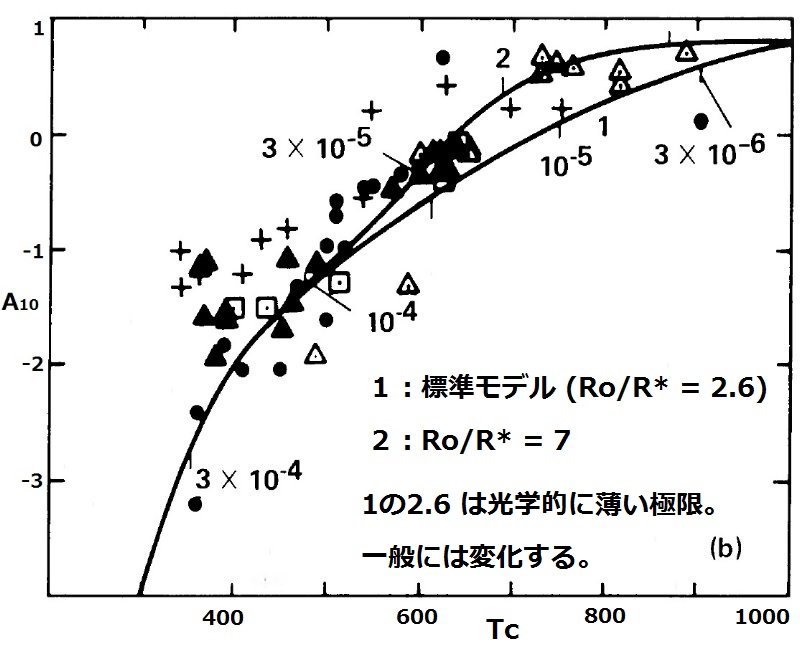
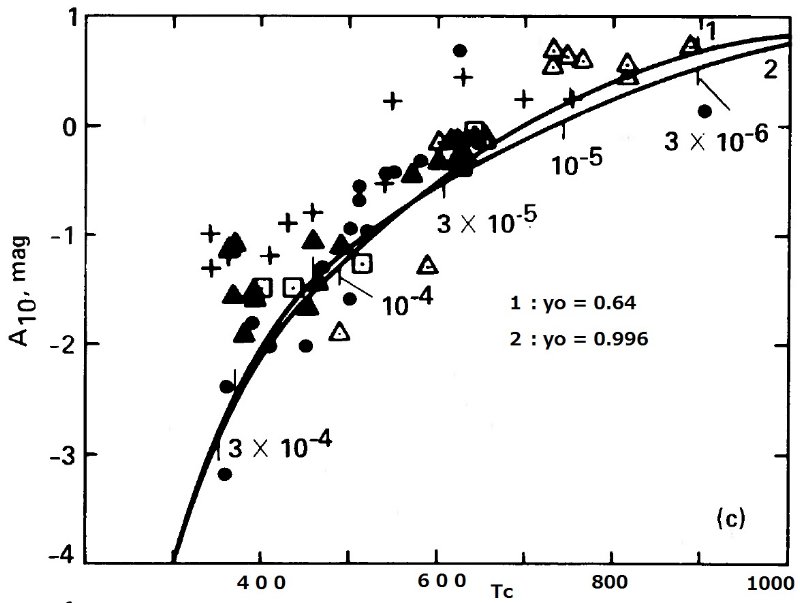
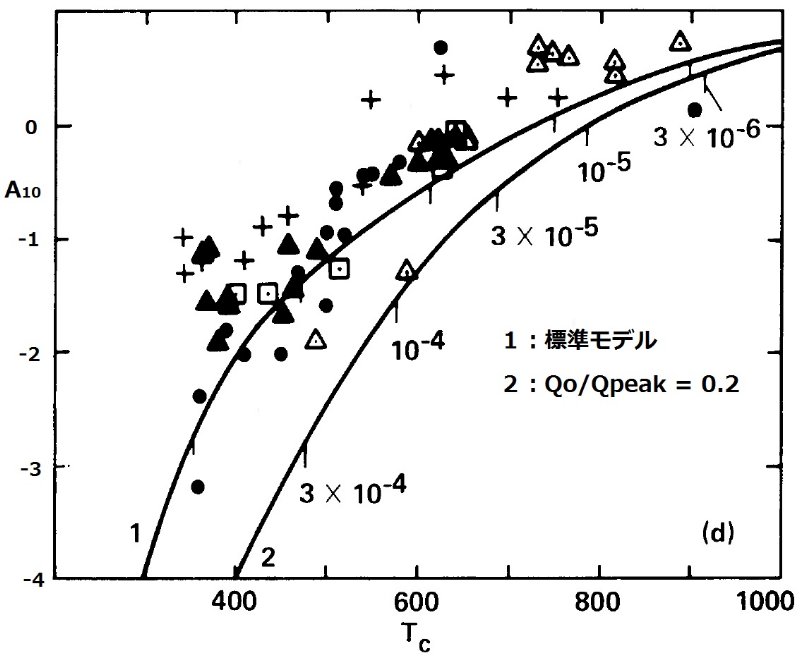
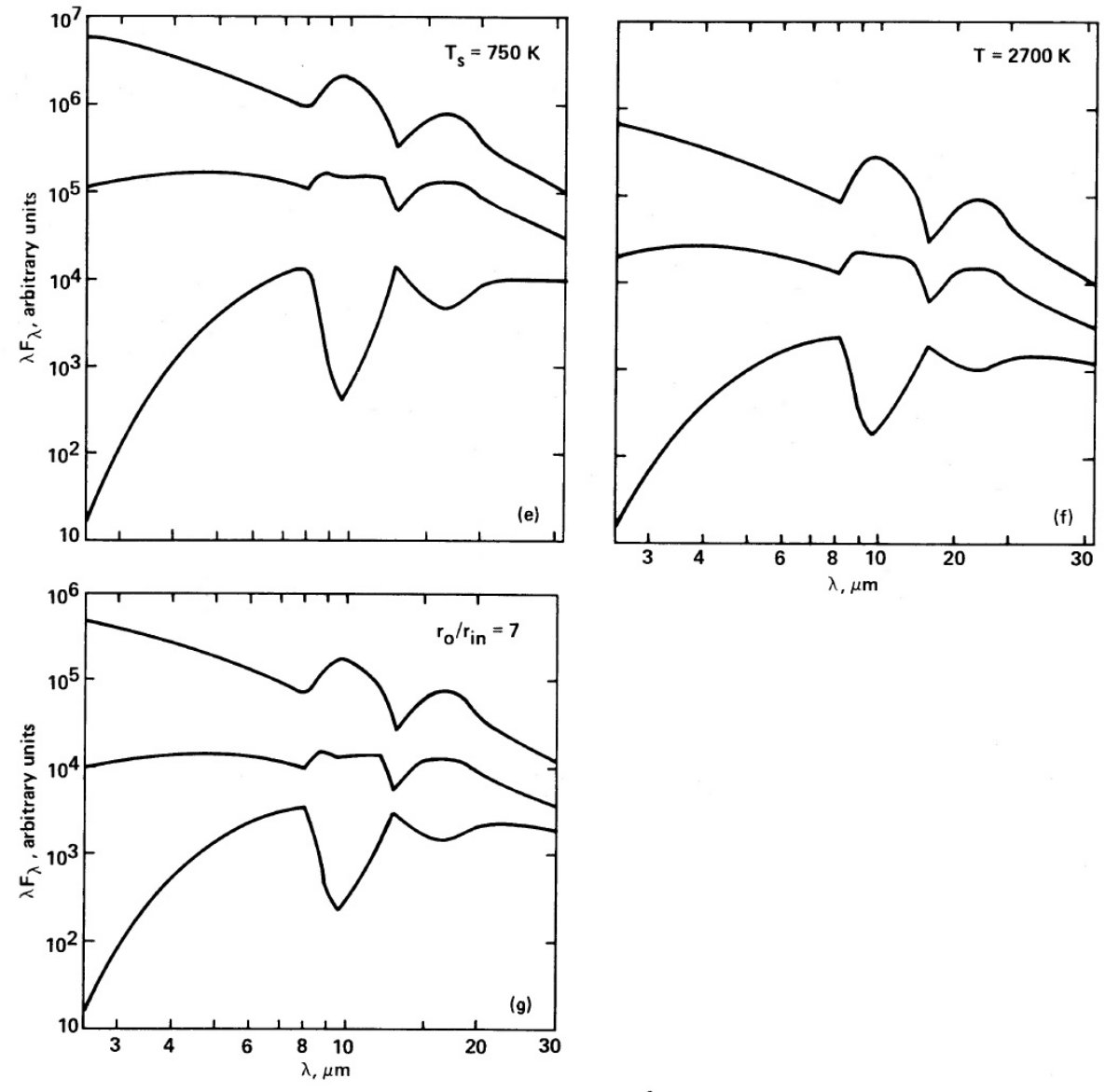
図１．放射スペクトルの解析表現、式 (5) 中の重み関数。１＝ 凝結温度 Ts 1000 K. ２＝ 凝結温度 Ts 750 K. ３＝黒体 B(T=1000K) 　式５と図１から分かること　 （１）光学的に薄い時には、マスロス率に無関係に、同じ Ts からは同じ放射 スペクトル が観測される。 　 （２）温度勾配のため、SED はＢＢより幅広になる。簡単には、 Td(r) = 3000 /λ(μm) までのダストが効くので、長波長ほど広い体積からの寄与 がある。 　 （３）式５の積分の勾配は黒体のレイリー・ジーンズ領域と似た形になる。し かし、その値は黒体の４に対し、３程度の緩やかなものである。 　 （４）もし、内側半径を一定に保つと、つまり r0 でなく、 Qabs/Qem を変動させると、低い Ts のシェルは低い平均 Td を持つようになり、 積分の形が変わる。しかし、 Ts > 750 K では λ > 5 μm の スペクトルはレベルが多少変わるだけで形はあまり変わらない。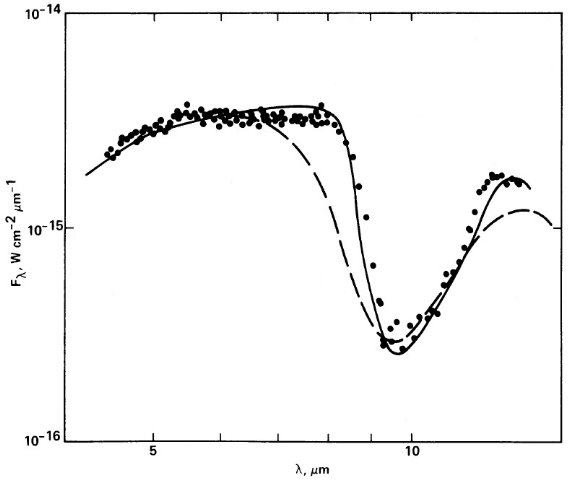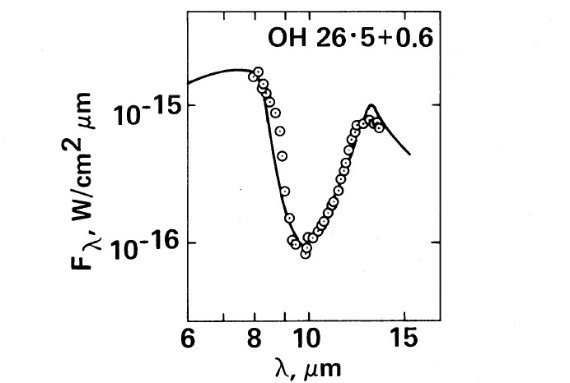 　10 μm 帯の形　 　光学的に薄いシェルからの 10 μm 帯の形はシェルパラメタ―からの影響 が小さく、ダスト吸収係数の形をほぼ忠実に再現する。もちろん、バンドの外 の波長帯の吸収係数を出すことは、光学的に薄い場合は困難である。 　近赤外 Qabs/Qem　 　光学的に薄いシェルの 近赤外 Qabs/Qem を観測から導くのも困難である。 というのは、それには r0 の値を知る必要があるからである。 　光学的に厚いシェル　 　光学的に厚いシェルの場合、ダストシェルからの赤外光もダストの加熱に効 くので、温度構造は光学的に薄い場合ほど単純ではない。この先はこの問題を 扱う。

　３．方法　

３．１．輻射輸達の式　 　Leung 1975, 1976a,b の準拡散法を使用する。この方法は輻射場の非等方性 も考慮されており、ダストの種類やサイズ分布も入れられるが、ここでは、 １種類の同一サイズのダストに限定する。 　３．２．ダストの吸光特性　 (この後に出る NIR, MIR, FIR をどう つないで全体の吸光強度が出来るのか、具体的な記述がない。肝心なところが ぬらりとしているのが残念。) 　３．２．１．近赤外域　 　レイリー粒子と仮定する　 　λ > 1 μm で、2π/λ ≤ 0.5 と仮定する。吸収、 散乱効率を以下の式で与える。 　　　Qabs(λ) = Q0[2/λ(μm)]　　　　　　　(6) 　　　Qsca(λ) = Q1[2/λ(μm)]4　　　　　　　(7) この領域では光学定数は一定で、Q1 = 1.6 10-4 と 固定する。Q0 はフリーパラメタ―にしておく。我々の標準モデル では Q0 = 0.018 としたので、Q1/Q0 = 9 10-3 となる。屈折率 n = 1.7 とすると、上の Q はグレインサ イズ 500 A に相当する。 (ここ、ついていけない。 ) 　取扱いの単純化　 　あとで述べるが、星周ダストの近赤外吸収は、遷移金属の電子遷移によると 考えられる。誘電物質の共鳴帯から遠い波長域で妥当な屈折率定数の仮定は 殆ど正当性がない。原則としては光学定数とサイズを仮定し、ミー計算を行う ことが出来る。しかし、それは近赤外吸収が何に起因するかが確定するまでは 待つべきと感じる。サイズ分布の仮定もフリーパラメタ―の数を増やすので、 単純に１パラメタ―で進む。 　３．２．２．10 μm 帯　 　３天体で異なるバンド形状　 　OH26.5+0.6, IRC10011, R Cas の予備的フィットの結果を図２に示すが、 それらは 10 μm バンドの形のみが異なる。モデル１＝OH26.5+0.6 のバン ド幅はモデル３＝R Cas より鋭く見える。しかし、注意しておくが、 FWHM の値自身はそう変わらない。

図２．仮定した星周シリケイトの吸収効率。単位は不定。１＝ OH26.5+0.6, 2 = IRC10011, 3 = R Cas のベストフィット。10 μm 帯の形、特に 8, 13 μm 付近、が違う。 Gillett,Jones,Merrill,Stein (1975) が導いたオリオンダストの 10 μm 帯の形は R Cas と最も近い。 　Qpeak = ピーク吸収効率　 　10 μm 帯は Qpeak = ピーク吸収効率に対して規格化される。 吸収強度 S(10μm) との関係は、 　　　Qpeak = 4aρsS(10μm)/3　　　　　　(8) ここに、ρs = ダスト物質の密度で、シリケイトでは 2.5 g cm -3 程度である。S(10μm) = 2 103 cm2 g-1 （実験で決めた非晶質シリケイト Day 1979） と仮定し、 a = 500 A とすると、Qpeak = 3.3 10-2. ダスト温度と放射スペクトルの形は Qabs/Q0 で決まり、Qabs の 絶対値ではないことに注意せよ。 　式８について　 τ=πa2QnsL n=ρ/(4πa3ρs/3) τ=(3/4)(Q/a)(ρ/ρs)L=SρL S=(3/4)(Q/a)/ρs Q=(4a/3)ρsS になった。お目出とさん！

　３．３．密度分布　

ここは面倒くさいので一部省略。 　星風解　 　　　v(dv/dr) = (GM*/r2(Γ-1)　　　　　　(12) Γ = ダストによる引きずり力/重力　であり、次の式で与えられる。 　　　Γ = (3Qrp/4aρs)(L*δ /4πcGM*)(v/vd　　　(13) Qrp = フラックス重み付き平均輻射圧効率。δ = ダスト/ガス。 ρs = ダスト物質の固有密度。光学厚みが大きいと Qrp は輻射が長波長側に移るにつれ小さくなっていく。しかし、計算では一定とした。 式 (12) を解くと、 　　　v = v∞[(x-y0)/x]1/2　　　(14) 　ここに、x = r/r0. 　　　y0 = 1 -(v0/v∞)2　　　(15) v0 はダスト凝結点での膨張速度で、大体音速程度である。 (臨界点と一致？ ) v0 << v∞ の時、Jura 1984 によると、 　　　v∞ = [2GM*(Γ-1)/r0]1/2　　　(16) 表１．標準モデルパラメタ―

脱出速度　 　ミラの典型的な値は、 Qabs/a = 2500 cm-1, ρs = 2.5 g cm -3, δ = 4 10-3, L* = 104 Lo, M* = 1 Mo, r0 = 2 1014 cm, v/vd = 1. これらから、v∞ = 13 km/s となる。 　密度分布　 　ダスト密度 nd は 　　　nd = n0/[(x-y0)1/2x 3/2]　　　(17) 　　　n0 = (dM/dt)δ/(4πr02 v∞md)(v/vd)　　　(18) y0 = 0 はダスト凝結点でいきなり v∞ で走り 出す解である。しかし、通常 y0 は １ に近い。その場合の密度 変化は図 3 に示した。 　コラム密度　 　式 (17) を x = [1, r1/r0] で積分して、 コラム密度を得る。 　　　Nd = 2n0r0[1 - (1-y0)1/2 ]/y0　　　(19) y0 = 0 (一定速度)の場合、Nd = n0r0. となる。y0 が増加するにつれ、シェル内側半径付近に溜まるダス トが増えて行く。y0 = 1 (境界で静止)の極限ではコラム密度は 倍の Nd = 2n0r0 となる. 　質量放出率　 　後のために、y0 と質量放出量の関係を書くと、 dM/dt=2πr0v∞[τ(10μm)/S(10μm)] (vd/v){y0/[1-(1-y0)1/2]} /δ S(10μm) = 10 μm ピークでの吸収強度である。 図３．加速域での密度分布。x = r/r0. 密度は n0 で 割って、(r/r0)2 を掛けて、一定速度への収束を 強調してある。曲線の数字は y0 の値である。

　４．星周シリケイトの近赤外オパシティ　

　４．１．観測された A₁₀ - Tc 関係　

Tc 　 　Tc = 3.8 - 12.5 μm でのカラー温度。3.4 μm データしかないものも ある。水の吸収が掛かるので、F(3.4) は位相により変光する。また、12.5 μm は10 μm バンドの端になる。それでも K-M カラーよりまし。 というのは、散乱の影響が少ないし、多くの天体データが揃っている。 　A10　 　　　A10　= 2.5 log(Fobs/Fc)　　　　　　　　　　(10) ここに、 Fc = 連続光のレベルである。連続光の求め方は書いていないが、 8.7 μm と 12.5 μm のフラックスの内挿らしい。 　A10 - Tc 関係　 　図４には、観測された A10 - Tc 関係を示す。A10 と Tc の間に一定の関係があることが判る。Tc は 3.8 - 12.5 μm のカラーエ クセス,つまり A3.8-A12.5 の指標であるから、これは A3.8 と A10 の相関と看做せる。 Kwan, Scoville 1976. 　変光の位相との相関　 　最後に強調したいのは、A10、Tc が変光の位相と共に変化する ことである。Evans, Beckwith 1977, Willems. de Jong 1982. その変化は、一般的な A10 - Tc 関係に沿っている。 明らかに、温度構造は位相と共に変化している。

図４．観測された A10 - Tc 関係。Tc = 3.8 - 12.5 カラー温度。 記号は文献の違いを表す。実線＝同じ星の異なる変光位相をつなぐ。二本の 矢印は Av = 30 mag の赤化。

　４．２．モデル　

　図５a: 境界温度　

１：標準モデル。Ts=1000 K, Teff=2000 K. ２：Ts = 750 K ３：Teff = 2700 K 　コメント　 　Teff が重要なのは、 Tc ≥ 650 K または A10 > -0.3 である。これは τ(10μm) ≤ 5 に相当。 　Ts が Tc - A10 関係に影響するのは、 Tc ≥ 500 K 又は A10 > -1 である。これは τ(10μm) ≤ 10 に相当する。 (　2: Ts=750K の方が 標準モデルよりフィットがよい )

　図５b: 内側半径一定　

１：標準モデル。Ts=1000 K, Teff=2000 K. ２：r0/r* = 7. ３：Teff = 2700 K 　コメント　 　r0 を一定に保つと、コラム密度＝光学的厚さが 大きくなると、内側温度が上昇する。その結果、 τ(10μm) > 10 で、 Tc - A10 関係に影響する。 (　 内側温度上昇で、To > Ts になってもそのまま放って置く ということなんだろうか？ )

　図５c: 境界速度　

１：標準モデル。Ts=1000 K, Teff=2000 K. ２：y0 = 750 K ３：Teff = 2700 K 　　　y0 =1 - (v0/v∞)2 ここに、v0 はダスト凝結点での膨張速度で、大体 音速程度を想定。加速域での速度分布は、x = r/r0 として、 　　　v = v∞[(x-y0)/x]1/2 である。 　コメント　 　y0 の Tc - A10 関係への影響は小さい。

　図５d: 近赤外吸収 対 10 μm 吸収　

１：標準モデル。Qo/Qpeak = 0.40 ２：Qo/Qpeak = 0.20 　Qo = 式(6) で定義される、Q(2μm)。 　コメント　 　τ(10μm) ≤ 5 では、 Tc - A10 関係が Teff, Tc に よって変化する。このため、ミラや IRC のように光学的に薄い天体では ダスト吸収の性質を一意に決められない。 (論理が良く分からない。) 一方、OH/IR 星のように光学的に厚い星では Tc - A10 関係が 主にダストの近赤外吸収の性質で決まる。これは光学的に厚くなると内側 境界条件が見えなくなってしまうからである。図５d では Q(2μm)/Qpeak = 0.2 と 0.4 について Tc - A10 関係を比較した。予想されるよ うに、同じ A10 に対し、 Q(2μm)/Qpeak が大きい（標準モデル） の方が低い Tc を与える。 (そうなのかな？ 2 μm で吸収が とよいからかな？ Tc は連続光部分で決まると思ったが、Qpeak はバンド だが、カラーにどう影響するのか？) 　これは A10 を決めるのに使う連続光 8.7, 12.5 μm が実際は 10 μm 帯のウィングに乗っているからである。

　図５e: 境界温度　

１：ダストモデル２。IRC 10011 採用。 ２：ダストモデル３。R Cas 採用。 　コメント　 　10 μm 帯のウィングの影響を示すために、ダストモデルを変えた 計算結果を示す。しかし、減光と放射の過程が複雑に関係し、簡単には 解釈できない。いずれにせよ、影響は小さい。

　４．３．近赤外吸収係数　

　４．４．マスロス率　

A10 - Tc 関係の利点　 　マスロス率は式 20 で与えられている。この式を用いてマスロスを計算した。 用いたパラメタ―は、 vd/v = 1, 　v∞ = 10 km/s, 　δ = 3 10 -3 S(10μm) = 2 103 cm2/g, 　L* = 104 Lo 図５には標準モデルについて、A10 - Tc 曲線上にマスロス率を マークした。光学的に厚いケースでは、A10 - Tc 曲線上の位置は ダストコラム密度に直接比例するから、導かれたマスロスはフリーパラメタ― の選択からかなりの程度まで独立である。このことは図５ a - e を詳しく調 べて裏付けられる。観測される 10 μm 帯の深さからコラム密度、マスロス率 を導く手法は複雑な輻射輸達効果により精度が下がる。同様に、Tc の観測から の導出も近赤外オパシティの知識を必要とする。、A10 - Tc 関係 は基本的にこの近赤外吸収率を 10 μm 吸収強度との相対比として較正する ものである。重要なのは、導かれた Qo/Qpeak がエネルギーバランスの式 (1) を通じて、シェル内側半径を直接決定することになることである。 　厚いシェルでの A10 - Tc 関係　 　A10 - Tc 関係が厚いシェルでは Ts に依存しなくなるというこ とに関してはコメントが要るだろう。 　Ts を下げると、シェル全体でダスト温度が下がるので、与えられた Tc また は A10 を得るために必要なコラム密度も低下する。(付録Ａ-4 を 見よ）しかし、対応するマスロスは内側半径の増加で相殺される。 　光学的に薄いケースでは、10 μm 放射帯強度から導くマスロス率は 仮定するダスト凝結温度に依存することを注意する。図５a と式 5 を見よ。 最後に、星光度 L はスペクトルのレベルには関係するが、光学深さには 関係しないのだが、マスロス率には内側境界の条件を通じて dM/dt ∝ L1/2 の関係がある。 　マスロス率の範囲　 　A10 - Tc 関係が輻射輸達関係の詳細に影響されにくいので、 この関係はマスロス率を決める際の第１候補になる。図５を調べると、 可視のミラ型星は < 10-5, IRC 天体では 3 10-6 < (dM/dt) < 3 10-5, OH/IR では 3 10-5 < (dM/dt) < 3 10-4 である。観測された最大値は 10-3 Mo/yr である。表２に、個々の星に対するマスロス率を 載せた。

表１．A10 - Tc 関係から導いたマスロス率 　変光効果　 　図５にある個々の天体のマスロスは表２にある。それらの不定性はファクター ３である。変光位相によるスペクトルの変化は図４の A10 - Tc 関係に沿っている。その原因は主に L の変化による。 　ダストの性質　 　ダストの性質もマスロス率の決定に重要である。ピーク強度 S(10) は 非晶質シリケイトの 103 から結晶の 104 cm2 g-1 まで変わり得る。我々は表１に示すように非晶質シリケイト を採用した。10 μm 強度は一般に SiO4 テトラへドラの数に 相関するので、 Mg, Fe を加えるとピーク強度は減る。

　４．５． A₁₀ - Tc 関係からのずれ　

　５．個々の天体　

　５．１．R Cas　

表３．R Cas, IRC 10011, OH26.5+0.6 星周シェルの観測及び導出特性。 　ベストフィットはダストモデル３　 　R Cas は M7e（位相 0.14） ミラである。10 μm 放射帯を持ち、光学的に 薄いことを示唆している。距離等のデータは表３に示すが、Ts は想定値である。 星の半径、光度は 3.5 μm 等級から出した (Forrest, Gillett, Stein 1975). v∞ は OH 観測から採った。y0 は式 15 に、 v0 = 2.8 km/s (T = 800 K の H2 音速）を入れて求め た。図６のベストフィットはダストモデル３を使用して、τ(10μm) = 0.10 の時に得られた。モデル３はオリオンで得られたものと似る。 モデル１と２は良いフィットを与えない。２−１節と付録Ａの議論から、 10 μm 帯の固有形状は他のフリーパラメタ―からの影響をあまり受けない ことが判るのでかなり確かと考えられる。例えば、10 μm 帯に対しては、 図６ベストフィット (Ts=1000K, τ(10)=0.10)とほぼ同じレベルのフィット が 2-2 節の Ts=750K, τ(10)=0.073 で得られている。Q0/Qext を動かした 時も τ(10) を調整するとやはり良いフィットが得られる。 　パラメタ―の不定性　 　逆に言えば、10 μm 付近のスペクトルだけでは Ts, y0, Qo/ Qpeak に制限を掛けることは難しい。強調したいのは、Ts, Qo/Qpeak を変え ても 6 μm 以下のスペクトルは殆ど変らない。

図６．R Cas の分光観測とモデルとの比較。実線＝図２のダストモデル３ を使ったベストフィット。破線＝モデル１の場合。 この波長域では観測される 光は光学的に薄いシェルによる星周減光を受けた光球からの輻射である。例え ば標準モデルでは τ(2μm) = 0.05 である。我々のモデルで、 Ts = 1000±300 K, Qo/Qpeak の不定性　30 % と仮定すると、 τ(10μm) の不定性は 40 % 程度になる。 　マスロス　 　標準モデルの τ(10μm) と y0 を用いてマスロス率を計算 した。Ts = 750 K モデルでは r0 が 70 % 大きくなるが、τ(10μm) が小さくなり、マスロス率としては 25 % 増加に留まる。同様に、Qo/Qpeak = 0.25 とすると、τ(10μm) が 50 % 上がり、r0 は 13 % 小さくなる。その結果マスロスが 40 % 大きくなる。 (Qo/Qpeak が下がり、 Ts 点が星に 近くなる。それが１３％、τ＝ｎｒで、それが　50 % 増しだから、新しい点の 密度は　63 % まし、それを元の点に戻すと、 元の点の密度が 63-12*2 = 38 % 増しになる。これがマスロス 40 %　増しの原因。) y0 もマスロス率に影響する。それらを考えるとマスロス率の不定性は 50 % である。

　５．２．IRC 10011　

図７．IRC 10011 の分光観測とモデルとの比較。実線＝図２のダストモデル２ を使ったベストフィット。破線＝モデル１の場合。 　IRC 10011　SED　 　IRC 10011 は 自己吸収 10 μm 放射帯 Merrill, Stein 1976 を示す。 これはかなり厚いシェルの証拠である。表２にはダストモデル２を用いたベスト フィットモデルのパラメタ―を示す。図８にはモデルスペクトルを観測と較べた。 τ(10) = 4.6 である。測光データの位相が異なるが、スペクトルの形はそう 変わっていないと仮定し、 Merrill, Stein 1976 に合わせた。

図８．IRC 10011 測光観測。観測値は 丸＝1.97, 三角＝1.51, 四角＝0.88, ひし型＝1.0 倍してフラックスレベルを合わせた。本文参照。 実線＝図２のダストモデル２を使ったベストフィット。 　ダストモデル２　 　10 μm 放射帯の固有形状は、図７に示すような自己吸収のために、やや 複雑である。モデル２が良いフィットを与えるが、測光データとの一致は不十分 である。他のダストモデルは 10 μm 帯を再現できない。図７にはモデル１ の例を示した。 12 μm 付近で高くなり過ぎることが判る。 　λ < 5 μm スペクトル　 　R Cas と異なり、λ < 5 μm スペクトルは Ts と Qo/Qpeak に 敏感である。付録Ａの図１５を見ると分かるように、 Ts を下げるか、Qo/Qpeak を上げるかすると、NIR フラックスを下げる。勿論 Ts と Qo/Qpeak で相殺さ せることは可能だが、完全なキャンセルは無理である。特に 3 μm 付近は 熱いダスト放射の寄与がある。 Ts が低いと、この寄与が消えるので修復が無理に なる。

図９a　IRC 10011 の 2.2 μm 規格化消失曲線。横軸＝月の縁からの角距離。 実線＝標準モデル(Ts=900K) 破線＝ Ts 750 K モデル。 　図９＝月の掩蔽観測　 　輻射強度の角分布はダストシェルの構造を調べる強力な道具である。短波長 λ < 3 μm では、強度分布はシェル内半径付近の熱いダストの 分布を反映する。長波長側では冷たい外側シェルの光が支配的となる。 図９には月の掩蔽を使った 2.2, 10, 20 μm の角度分布　Zappala et al 1974 を示す。予想されるように、長波長放射は中心から広がっている。 　Ts が決まるか？　 　Ts は短波長輻射の角度分布に大きく影響すると予想される。理論的強度分布を 図９の実線 Ts=900 K, 破線 Ts 750 K の二つに対して示す。仮定した 光度とシェル半径は観測の際の測光値と合わせるため、標準モデルより少し 小さい、 L = 4.6 10 3 Lo, r0 = 4.9 1013 cm とした。2.2 μm 図は Ts = 900 K 曲線が良く合うが、 Ts = 750 K を 否定するほどではない。 　不定性　 　我々は Ts と Qo/Qpeak の不定性を 10 % と評価する。τ(10) は　15 % である。式 15 から導くマスロスは 1.9 10-5 Mo/yr である。 この誤差は 10 % 程度。

図９b．IRC 10011 の 10 μm 規格化消失曲線。横軸＝月の縁からの角距離。 実線＝標準モデル(Ts=900K) 破線＝ Ts 750 K モデル。 図９c．IRC 10011 の 20 μm 規格化消失曲線。横軸＝月の縁からの角距離。 実線＝標準モデル(Ts=900K) 破線＝ Ts 750 K モデル。

　５．３．OH/IR 26.5+0.6 　

図１０．OH 26.5+0.6 の測光とモデル計算の比較。実線＝ダストモデル３ を使ったベストフィット。 　ダストモデル３　 　OH/IR 26.5+0.6 = AFGL 2205 は深い 10 μm 吸収帯を示す。中心星の 有効温度は不明である。そこで Teff = 2000 K を仮定した。図１０、１１ は τ(10μm) = 28.0、ダストモデル３のベストフィットを示す。 図１１にはオリオントラペジウム放射スペクトルで合わせた曲線も示すが、 幅が広すぎる。マスロスは 2 10-4 Mo/yr である。 近赤外オパシティ　 　ベストフィットは全体として観測と合うが、いくつかズレが見える。第１は 3.4 μm 付近で、第２は 20 μm の先である。近赤外の差は 3.4 μm 付近で吸収が弱く、3.4 - 10 μm に掛けて減光則が平坦になり、2.2 - 3.4 μm では急になることを意味する。 IRC 10011 のモデルフィットでも同じ ような兆候が見えた。これは、近赤外で強まる吸収がシリケイト中に溶け込ん だ遷移金属の電子遷移に依るならば、予想されることである。 　中間赤外オパシティ　 　中間赤外 λ > 20 μm では我々のモデルが仮定しているよりは 弱い吸収らしい。OH/IR 星の IRAS による観測の解析もそれを支持する。 遠赤外のオパシティの波長依存性はもう少し詳しい解析を必要とする。

図１１．OH/IR 26.5+0.6 の分光測光観測 (Forrest et al 1978) と モデルの比較。実線＝図２のモデル１を使ったベストフィット。破線＝オリオン 10 μm バンドを使ったベストフィットモデル。 　スペクトル変化の説明１　 　 Forrest et al. (1978) は変光の２位相で分光測光観測を行い、この星の光度が 50 % 低下した時に 10 μm シリケイトバンドの光学的深さが 60 % 上がる ことを示した。光度変化の影響を調べるために、星の半径を一定にしたままで 光度だけ低下させた。これは Wallerstein (1977) Wallerstein 1977 がミラ型星で見出したことである。シェルが光学的に厚い ため、付録 Ae に述べたように、有効温度は放出スペクトルには何の影響も 及ばさなかった。密度構造は変光位相で変わらないと仮定している。しかし、 光度が変わるために温度構造は変化する。特に、シェル内側半径の温度は 830 K となった。シェル全体でのこの温度低下は 10 μm 吸収強度の増加 を引き起こす。このモデルは図１２の観測結果を上手く説明する。 (密度構造が変わらなければ、光学的 深さは同じはず。変だ！ ) 　スペクトル変化の説明２　 　別の説明はこうだ。ダスト凝結温度を一定とする。すると内側半径は光度に 依って変化し、その結果式１９にあるように光学的深さが変わる。こうして 光度が下がると、光学的深さが増し、冷たいスペクトルになる。

ビジビリティ　 　OH25.6+0.6 の角度測定は Dyck et al 1984, Fix, Cobb 1988 により行われ た。図１３のモデルは Hankel 変換を用いたビジビリティ曲線である。 　密度分布　 　式１７の光学的に厚い場合への補正について。 図１２．OH/IR 26.5+0.6 の分光測光観測 Forrest et al 1978 とモデルの比較。 観測時光度 L は図１１の時の半分くらい。実線は標準モデルと同じ密度分布 だが、光度は低いモデル。 (同じ r0 なのか？ L が小さくなるので、 To < Ts になってしまう。 )

　５．４．議論　

10 μm 吸収プロファイル　 　３つのサンプルを較べると、光学的に薄い R Cas の 10 μm のバンド巾 は最も狭く、IRC 10011, OH/IR 26.5+0.6 と光学深さに連れて、広くなっていく。 10 μm 帯の固有プロファイルの変化は μ Cep に対して Rogers, Martin, Crabtree 1983 が、幾つかの巨星に対し Pegourie, Papoular 1985 が述べている。 　説明１＝サイズが原因？　 　Pegourie, Papoular 1985 は、この差がダストサイズが原因とした。しかし、 以下の理由により否定される。 （１）13 μm での差は 8 μm での差より大きい。これはサイズ効果の予想と 逆である。 （２）３つの天体で、Qo/Qpeak は大体等しい。これもサイズ効果ではないことを 意味する。 　説明２＝光学定数は？　 　Plendl 1970, Tielens, Allamandola 1987 は温度が下がると吸収帯が鋭く なると述べた。光学的深さが増加すると、平均温度は下がるので、傾向とし ては合っている。ただ、シリケイトの光学定数に関する温度依存性は分かって いないので定量的評価は出来ない。注意すると、この仮説はオリオンの幅広な バンド Tielens, Allamandola 1987 と Sgr A 方向の星間吸収プロファイル との差の説明でも述べられていた。 　説明３＝ダスト構造の違い？　 　第３の説明はダストの構造または組成の違いで、特に光学的厚みが増加した 際に、シリケイトの熱平衡凝結層の温度が上がる結果ダストの光学的性質が 変化するという説明である。この考えでは、ダスト形成層 3 - 7 r* の位置は脈動で決まり、熱平衡凝結温度では決まらない。凝結シリケイトの温度 は熱平衡凝結温度よりずっと低く、極度に非晶質の物質が生じる。Tielens 1983, Tielens, Allamandola 1987 を見よ。ダスト凝結層で形成されたダストは、 光学的厚みが大きいほど高温である。その結果できるダストはより結晶性が高い。 実験室の結果に依ると、グレイン温度が高いほど結晶度は上がり、10 μm 帯が鋭くなる。Kratschmer, Huffman 1979. 参照。しかし、 OH 26.5+0.6 と IRC 10011 の数値モデルは同じ T = 1000 K という内側温度を示しているので、 この説明は怪しい。

図１４．OH/IR 25.5+0.6 の解析的密度分布と標準モデルで加速を計算するため の局所輻射場を使った二次近似との比較。図３と同じく (x2/n 0)を掛けて規格化した。 　 　表４＝マスロス　 　表４ではモデルフィットから求めたマスロスを他の研究からの値と比較した。 最後の列は Salpeter 1974 の次の式に基づいている。 　　　dM/dt = L*τ/cv∞　　　　　　　(22) 計算したマスロスは距離に比例することを注意する。 (良く分からないが、まあいいや。 )

　６．まとめ　

　付録Ａ　

付録Ａ−１　マスロス率　 　コラム密度を上げて行くと、　10, 20 μm 放射帯総フラックスが増加する。 しかし、それらの波長で τ > 3 になると、自己吸収が始まり、 τ > 6 では吸収帯と変わる。ダスト凝結温度は 1000 K 以下なので、λ < 3 μm ではフラックスはダスト放射でなく、減光を受けた星の光である。 ダストコラム密度をさらに上げると、スペクトルは赤くなっていく。2 μm 領域のスペクトル変化は Qo/Qpeak を通じて 10 μm 変化と繋がっている。 　付録Ａ−２　ダスト吸光の性質　 　Qo/Qpeak の影響　 　 Jones, Merrill (1976), Bedijn 1977 が示したように、Qo/Qpeak の値はシェルスペクトルの形に決定的 な影響を及ぼす。光学的に薄い、&tau(10) ≤ 3 のケースでは、コラム密度 一定のまま、この比を下げると 10, 20 μm 放射帯を弱める。図15a, b を 見よ。注意するが、この時内側シェル境界半径は小さくなる。その結果、 Qo/Qpeak が低下すると、温度勾配が同じでも暖かいダストの総量、つまり 10, 20 μm 放射を行う総質量が減少するのである。　 　厚いダストシェルのスペクトル　 　ダストコラム密度が τ(10) > 3 に上がると、同じコラム密度を持つ 標準モデルの 10, 20 μm 付近のスペクトルとの差は小さくなって（図15a,b を見よ）来る。これは基本的にこれらの波長での放射がダストシェル外側の 冷たいダストから来て、そこでは星の NIR 光よりはダストからの λ > 10 μm 輻射の方が加熱に効くからである。Ts が不変だから、内側 シェルのダスト温度は変わらない。 　近赤外スペクトル　 　勿論、星からの光が支配的な λ < 3 μm スペクトルは Qo/Qpeak に強く影響される。同じコラム密度＝同じ 10 μm 光学的深さ、で較べると、 Qo/Qpeak が小さいモデルの近赤外光学的厚さは小さく、近赤外カラーは青く なる。この効果は星周シリケイトの近赤外オパシティを決めるのに使える。 Jones, Merrill (1976), Bedijn 1977 参照。

表５．モデルの 2.2 μm フラックス。