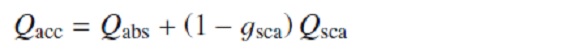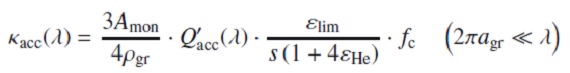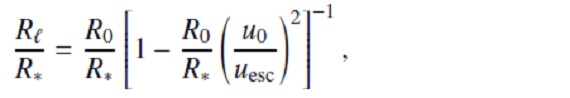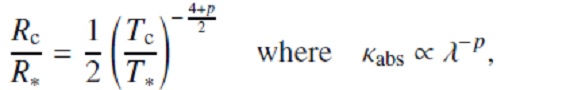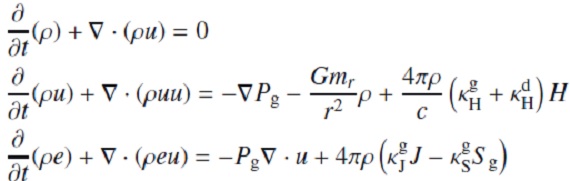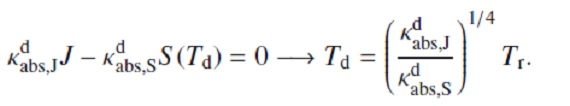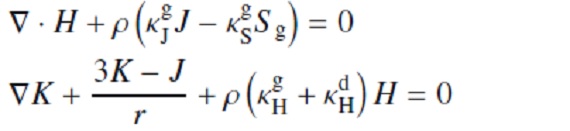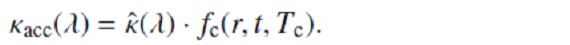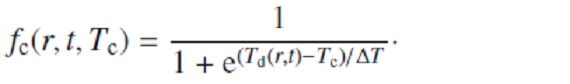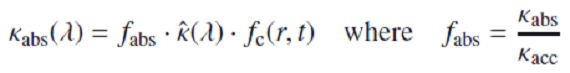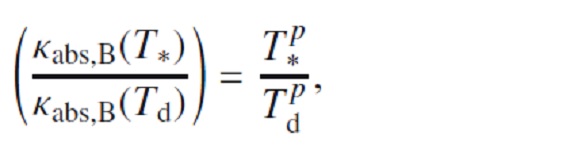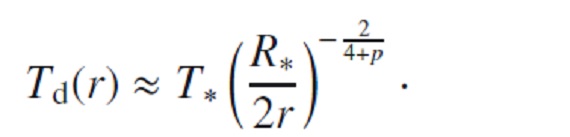Exploring Wind-Driven Dust Species in Cool Luminous Giants
I. Basdic Criteria and Dynamical Models of M-Type AGBs

　アブストラクト　

　１．イントロダクション　

　２．ダスト駆動星風：定性的な描像　

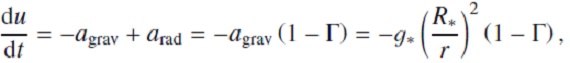
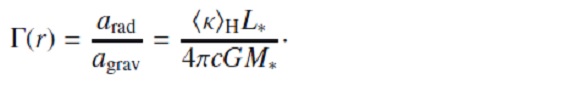
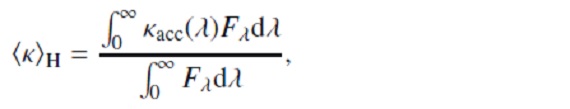
２．１．星風の輻射加速　 　基本方程式　 　流体中の質点の運動を考える。その運動方程式は、 ここに、g*=GM*/R+2 は星表面重力加速度、Γ=　輻射と重力 の加速度の比であり、以下の様に表される。 上式はフラックス平均の(単位星間ガス質量当たり？)ダストオパシティ。 κacc(λ) = 波長λ での （星間物質単位質量当たり）オパシティである。 次に臨界オパシティ κcrit を以下の様に定義する。 これは上の第２式で Γ = 1 とした時に当たる。

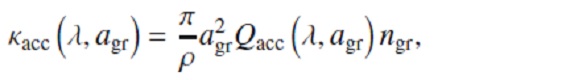
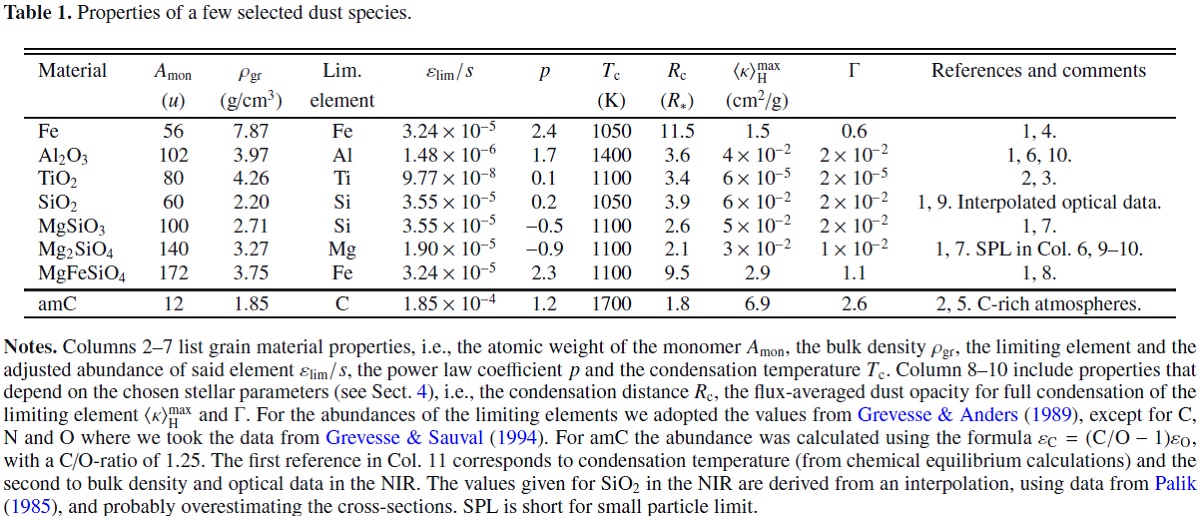
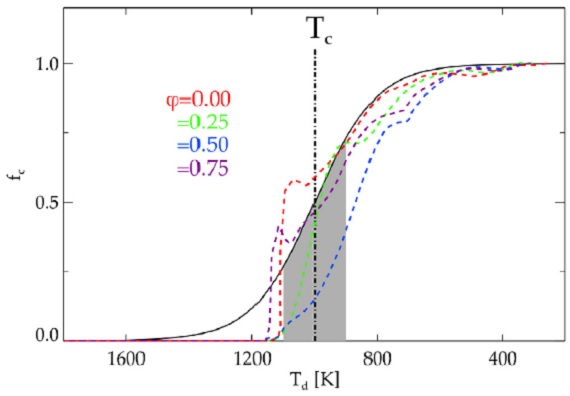
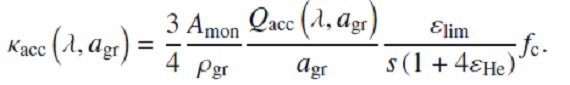
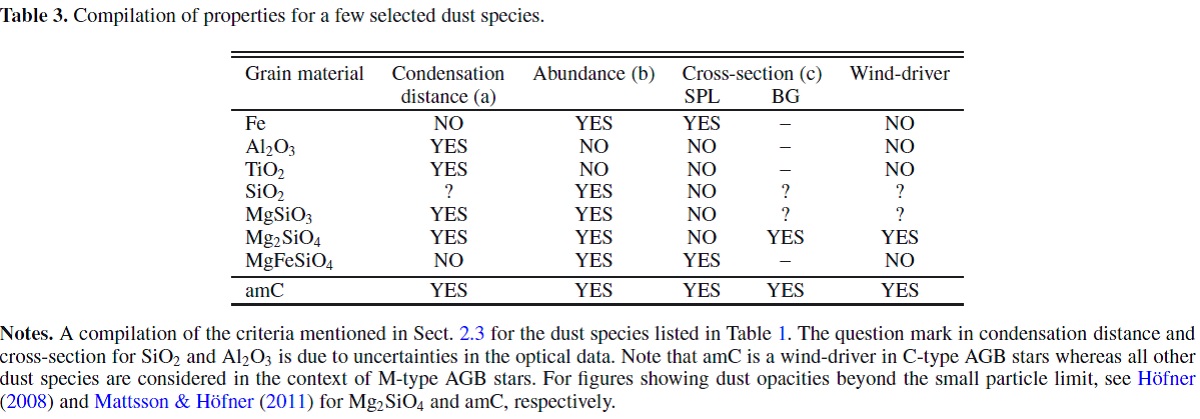
オパシティ　 　簡単のため、グレイン半径 agr = 一定とする。すると単位質量 当たりのオパシティは ここに、ngr = ダストの数密度。Qacc = 輻射断面積/幾何断面積である。 Amon = 単量体原子量, ρgr = グレイン物質の巨視密度, εlim = 制限元素の存在比, εHe = ヘリウムの存在比、 fc = 制限元素のダスト化比率、s = 化学等量係数、とすると、 と書き直される。Mg2SiO4 グレインの場合、最小元素 は Si であるが、 単量体(monomer) 一つに Mg は二つ消費されるので、s = 2 の Mg が制限元素となる。 星間物質単位体積当たりオパシティ ρκ = πa2Qn 水素原子の数密度 nH = ρ/H/(1+4εHe) ダストに組み込まれた制限元素の数密度 nlim = nH εlimfc ダストグレイン１個内の制限元素数 Nlim = s(4π/3)a3 ρgr/(AmonH) ダストの数密度 n = nlim/Nlim = (nHεlimfc)/[s(4π/3)a3 ρgr/(AmonH)] = [ρ/H/(1+4εHe)][εlimfc] [3AmonH/(4sπa3ρgr)] κ = [a-1Q/(1+4εHe)][ε limfc][3Amon/(4sρgr)] =[3Amon/(4ρgr)][Q/a][ε limfc/s(1+4εHe)]

減光効率 Q　 　吸収と散乱を含んだ効率 Q は、 ここに、gsca = 非対称ファクター。小粒径極限では、 Qabs ∝ a, Q ∝ a4 なため、 散乱は無視できるようになり、Q' = Qabs/a とおくと、 　２．２．凝集距離 Rc と浮揚距離 Rl　 　浮揚距離 Rl　 　衝撃波で持ち上げられたガスが r = Ro で速度 u0 の自由運動 に移ると仮定する。星表面の脱出速度 uesc = (2M*G/R*) 1/2 とすると、 　Ｍ* ＝１Mo, L* = 5000 Lo, Teff = 2800 K の場合、uesc = 36 km/s である。CO 第２倍音の観測から得られる視線速度は 10 - 15 km/s である。 Nowotny10 の動力学モデルによると、これらのラインが形成されるのは星表面 から上空 1.5 R* までの間である。そこで、 u0 = 15 km/s, Ro = 1.5 R* を仮定すると、上式から Rl = 2 R* となる。 　u02/2 - GM*/Ro = - GM*/Rl 　1 - u02Ro/2GM* = Ro/Rl 　Rl/R* = (Ro/R*)[1-(Ro/R*)(u0/uesc)2] -1 　凝集距離 Rc　 　κabs ∝ λ-p を仮定すると、ダス トの熱平衡式は 　　4(R*/Rc)2∫B(ν,T*)νpdν= ∫B(ν,Tc)νpdν 　　4(R*/Rc)2T*4+p = Tc4+p であるから、 図１には Rc/R* = 2, 4, 10 のラインを p - Tc図上に描いた。 かなり変わった発想の図に思える。式で表すと 2log(Rc/R*)=-(4+p)log(Tc/T*)-2log2 p = -4-2log(2Rc/R*)/log(Tc/T*) こりゃダメだ。変数は p, Tc, Rc/R*, T* か。図１は p-Tc 面上で 二つの T* に対して、Rc/R* ＝一定の線を３本描いた。もっと分かりやすいのは、 Rc/R*-T* 面上に、いくつかの p に対して、Tc = 一定の線を描くことでは？

図１．凝結距離 Rc/R* ＝　2, 4, 10 のライン。実線は T*= 2800 K, 破線は T* = 2500 K. 　p の正負　 　正の p を持つ物質は星表面に近いと吸収効率の方が放射光率より高くなり がちで、そのため凝結距離が遠くなる。一方、負の p を持つと逆の傾向となる。 負の p というのは信じがたいが、あるんだ。しかもシリケイト！ 例えば、Feシリケイトの場合、 Tc = 1100 K, p = 2.3 である。すると、 T* = 2800 K に対し、 Rc = 10 R* となり、浮揚半径を大幅に超過する。一方、 Fe フリーシリケイトでは Tc = 1100 K, p = -0.9 で、Rc = 2 R* である。この 距離なら浮揚半径内となる。 　熱平衡？　 　イントロダクションで述べたように、相平衡は AGB 星におけるダスト形成 を正しく記述しない。 Gail10 の詳細なモデルでは、冷却効果が凝結温度より ずっと低い温度にしないと形成過程が進行しない。従って、熱安定を仮定する と凝結距離を実際より小さく見積もる結果となる。Tc を 10 % 下げると、ｐ によるが、Rc は 17 - 41 % 大きくなる。この様に、いくらかの誤差はあるが、 炭素質ダストと Fe-フリーシリケイトの　Rc が 2 - 3 R* に収まることは 確かであろう。

２．３．星風駆動源の条件　 　グレインの性質　 　あるグレイン物質が星風駆動源として適当かどうかを決めるためには 次の性質を調べる必要がある (a) Rc(Tc, p, T*) (b) εlim (c) Qabs と Qsca 特にフラックス極大波長域での。 詳細なモデル計算には時間変化、例えば成長率、などの考慮が必要である。 　選別　 　特定の物質が星風駆動源として適当かどうかを判別するには、 （i）(Rl/R*) と (Rc/R*) が十分に小さいか。 （ii）εlim と fc = 1 (最高に良い条件)で、 κacc を計算する。 （iii）適当な星フラックスで計算した ⟨κ⟩H > κcrit か。 以上を全て満たす物質は星風駆動源として更に詳しい研究の対象となる。図２上 に示す物質の図２下のフラックスに対する ⟨κ⟩H を表１に示す。

図２．上：小半径極限でのグレイン半径当たり効率 Qacc/a gr と波長との関係。破線＝指数則フィット。斜線部＝フィット 波長帯。下：黒線＝Teff 2800 K の星スペクトル。赤線＝BB

　３．詳細 RHD モデル　

３．１．ガス力学と輻射場　 　質量、運動量、エネルギー保存則　 　質量、運動量、エネルギー保存則は次のように書かれる。 ここに、u=動径方向速度、ρ=ガス密度、Pg(ρ,e)=ガス圧力、 mr=半径 r 内部の星質量、e=ガスの単位質量当たり内部エネルギー である。式から分かるように、ダストが輻射から受けた運動量は一瞬にして ガスに渡されると仮定している。ダストの吸収と散乱効率は共に運動量獲得に 寄与し、まとめてκHd に含まれる。 (ダストからガスへの熱移転なし？ ) 　ダスト温度　 　ダストのエネルギー収支は次の式で表される。 ここに、Tr ＝ 4√(Jπ/σ) = 輻射温度、 κabs = ダストオパシティの吸収部分である。 　モーメンタム方程式　 J, H = 輻射強 度 Iν の周波数モーメンタムで、輻射方程式のゼロ次と１次 モーメンタム方程式を解いて求める。 注意すると、上の最初の式のダストオパシティの項はキャンセルして消える。 その前にあるように輻射平衡を仮定しているからである。 波長毎の輻射方程式を解いて、 Jν, Hν, Kν を求め、 でモーメンタム平均オパシティを求める。LTE を仮定し、源泉関数はプランク 関数 Sg = Bν(Tg), Sd = Bν(Td) とする。注意 しておくが、周波数依存の輻射方程式を解く際に散乱光は無視した。散乱光は 運動量獲得に関しては大きな役割を持つ。しかし、散乱光自体は輻射場を大きく は変えない。特にダストが成長して前方散乱が強くなるとそうである。

図３．凝結率とダスト温度の関係。 　３．２．パラメター化したダストモデル　 　ダストのパラメター化　 　Bowen88 にヒントを得てダストのパラメター化を行った。それは、 　fabs　 　散乱と吸収がグレインに与える影響を区別するため、我々は fabs = κacc 中の吸光部分の割合、を導入する。

　４．モデルパラメター　

星パラメター　 　動力学モデルに選んだ星パラメターは M* = 1 Mo, L = 5000 Lo, T* = 2800 K, 太陽組成である。内側境界での脈動は速度振幅 4 km/s とする。 　臨界オパシティ　 　ダストは、κ0, p, Tc, ΔT で記述される。 κcrit = 4πGM*/L* を計算すると 2.6 である。 SI で、G＝6.7 10^(-11) N・m^2・kg^(-2), Mo= 2 10^30 kg, L*=5000*3.85 10^26 W. を代入すると κcrit = (4π*6.7*2/5000*3/3.85)10^(-11+30-26+8) N・m^2・kg^(-2)・kg・m/W/s = 0.26 m^2/kg = 2.6 cm^2/g 単位ぐらい書けよ！

パラメター化ダストオパシティ　 パラメター化したダストオパシティで、 p = 0 の場合に、 κ0 = 3.0 cm2gm-1 とする。そして他の p の対しては &lang:κ&rang:H が 同じになるように調整する。&lang:κ&rang:H の計算に 当たっては黒体でなく、モデル大気を使用する。こうして、 &lang:κ&rang:H = 3.0, Γ = 1.1 の動力学モデルを 計算することになった。 　ΔT　 　ΔT = 100 K とした。この値自体は結果にあまり影響しない。 　モデルグリッド　 　こうして、 p と Tc を変えて、モデルグリッドを計算した。最もありそう な組合わせをカバーするため、 p = [-1, 2.5], Tc = [700, 1700] K の 範囲を選んだ。さらに、 fabs = 0.5 - 1.0 の範囲で計算した。

　５．結果　

図５．赤＝ダスト、黒＝ガス、青＝輻射温度(Tr) の距離変化。 Tc = 1500 K, ψ = 0.5. 上　p=1, 中 p=0, 下 p=-1. 破線＝静水大気。 　５．１．星風駆動源の制限　 　高 Tc で 負または緩い正の p 　 　図４を見ると、(Tc, p) のどのような組み合わせが星風を駆動するのに 必要かがはっきりと分かる。Tc が高く、波長と共に NIR 吸収が強まる、 またはゆっくり低下するダスト物質は星表面近くで凝結し、 M-AGBs の 星風を駆動できる。例として、Tc = 1700 K, p = 1.5 という急勾配の 物質でも星風を駆動可能である。しかし、 Tc < 1400 K だと、p ≤ 0 が必要となる。

図６．Hofner08 の Mg2SiO4 グレイン質量放出モデル。 赤＝ダスト、黒＝ガス、青＝輻射温度(Tr) の距離変化。 破線＝静水大気。 　星風と非星風の境界　 　星風と非星風の境界線は下式で決まる凝結距離一定線と形が似ている。 それは、前に述べた質量放出の二つの段階をつなぐ上で凝結距離が重要な役割 を担っていることを示す。そうは言っても図９を見れば、単純な評価では詳細 モデルの値を出すことが無理と分かる。境界の位置は、星のパラメター、脈動 振幅、その他に影響されるのである。また、ダストの単純なパラメター化は Td < Tc になると直ちにダストオパシティが働き出すと仮定しているので、 ダスト形成の効率を過大評価していることになる。 　５．２．グレイン温度の傾向　 　p < 0 だと星近くでダスト形成　 　p < 0 の場合、長波長側での放射効率は短波長側での吸収効率より高い。 このために、ダストは吸光より放光がしやすいため、グレイン温度は低くなる。 その結果、グレイン形成距離は星表面に近い。p > 0 ではそれと正反対の事 が起きる。この傾向は図５にはっきり見られる。p = 0 を境に 赤線と青線の 上下が逆転することに注意せよ。 　詳細モデル　 　比較のために、図６にはMg2SiO4 グレイン形成 と光学的性質を詳細に組み入れたモデルを示す。この物質はパラメター化 では p = -0.9 となる。しかし、詳細モデルではダスト温度はそれより更に 低くなっている。

　５．３．質量放出と星風速度　

　５．４．グレイン透明度の効果　

　６．議論：　グレイン物質　

図９．

表４．他の候補物質の p, Tc

　７．まとめ　

　App B. 凝結距離　

輻射平衡は輻射輸達の式から 　　κabs,JJ - κabs,SS(Td) = 0 　　光学的に薄い大気を考え、 Jλ = W(r)Bλ (T*) ここに W(r) = [1-√(1-(R*/r)2)] は幾何学的希釈ファクター κabs,BW(r)Bλ(T*)= κabs,BBλ(Td)