| 論文シリーズIIIで紹介した動流体力学と周波数依存輻射方程式を結合した 動的大気モデルに基づいて、 C-AGB モデルスペクトルを計算した。分子 CO, CH, CN, C2, CS, HCN, C2H2, C3 を大気構造と合成スペクトルの計算に含めた。 | 0.5 - 25 μm における合成スペクトルと観測スペクトル、カラーとの比 較を、TX Psc, WZ Cas, V460 Cyg, T Lyr, S Cep について行った。 変光の様々な位相で集められた観測結果と、単位相でのモデルスペクトルとの 一致は 0.5 - 5 μm では良い。より長波長では我々のマスロスモデルは 初めて、これまでの疑問=なぜ全ての静水大気モデルとマスロス無しの流体 動力学モデルが予想していた 14 μm 付近の強い吸収帯が観測では存在し ないか、の説明に成功した。 |
2.1.動力学モデルピストン内側境界は速度振幅 Δu, 周期 P のサイン関数型の運動を与えられている。 内側境界での光度は内側半径の二乗に比例とフリーパラメター fL の 掛け算の形で変化する。以前の扱いは fL =1 に対応し、フラックスが 固定されていた。 |
外側境界 静水大気初期モデルの外側境界は光球のすぐそばに位置していた。動力学計算では、 星風ナシの時には大気の最上層を境界にする。星風が発生すると、星風を追跡できる R = 20 - 30 R* の位置に外側境界を置く。 |

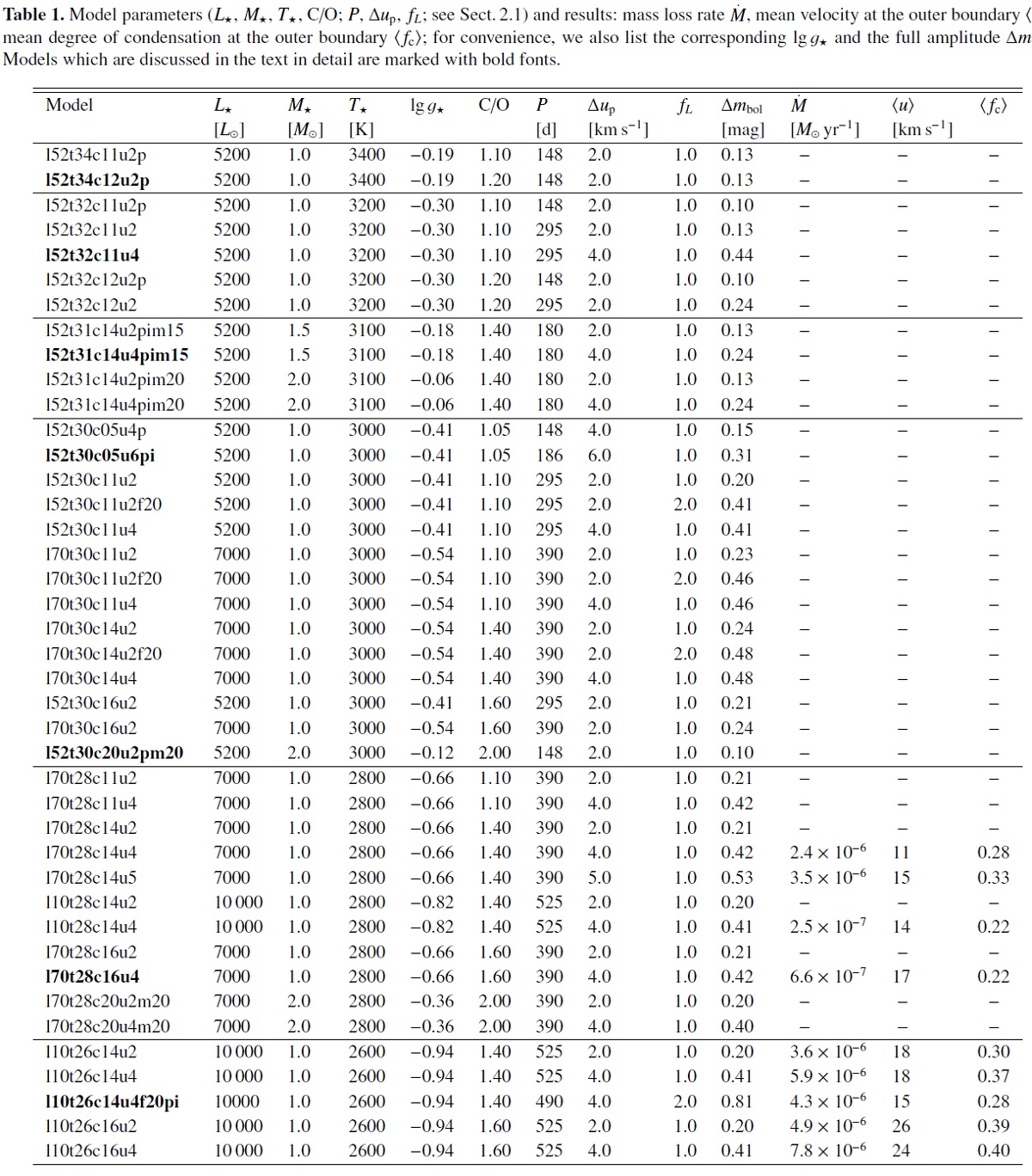
2.2.モデルパラメターと星風の性質モデルのパラメターと性質表1に計算で使用したモデルのパラメターと性質をまとめた。 星風が発達した場合には質量放出率と星風速度 u、それに凝結の割合 fc も 載せた。どの計算でも 星風の発生は禁止していないが、多くの場合、ダスト フリーの脈動大気に終わった。 ダスト層が薄い星 実際、今回のモデルパラメターは、厚いダスト層には囲まれていない星から 選んだ。厚いダスト層は観測との比較を難しくするからである。唯一 S Cep のみはかなりマスロスが強く、短波長側スペクトルが変形を受ける。 薄い星風の計算は厄介 モデル面からは薄い星風の計算は厄介である。星風なしから星風アリへの 転移はかなり狭いパラメター領域で起こる。AGB 星でのダスト形成は平衡から 遠い条件で進行する。熱力学的条件に対するダスト形成の応答は強い非線形性 を示し、さらに強いフィードバック効果を持つ。それは、モデルのグリッドを 非常に細かく切る必要を意味する。それは現実的でない。したがって、我々は 低マスロス星にはマスロス無しの星を使用する。 |
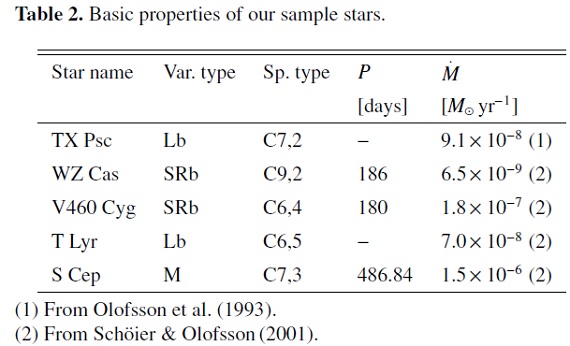 表2.サンプル炭素星の基本性質 2.3.モデルパラメターと星風の性質 |
|
過去30年間次の4天文台で集められてきたデータを使用する。 (i)Kuiper Airborn Observatory (1976-1978) 1.2 - 4 μm. 4天体。 (ii)Carlos Sanchez Telescope (1983, 1985) 1.0 - 4.2 μm. |
(iii)CRSOP/KPNO 1998. 1.08 - 4.16 &mu:m.
(iv)SWS/ISO. 1995 - 1998. 2.36 - 45.2 μm (v)Baumert 1972 狭帯干渉フィルター観測 |
4.1.フィット条件とモデルグリッドスペクトル診断Gautschy-Loidl 2001 は次の吸収強度が診断に使えることを示した。 Teff C2H2/HCN 吸収帯 2.5, 3, 3.8 μm SED C/O C3 吸収帯 5.1 μm Gautschy-Loidl 2001 によると、C2H2/HCN の 0.5 - 2 μm での吸収は C2 データに不確実な所があり、 2次的な用途しかない。 合成スペクトル 図1にモデル l52t32c1 の極小期(ψ = 0.5)合成スペクトルと、各分子 からの寄与を示す。 モデルパラメター ピストン速度 Δup の大きさはスペクトル変化に決定的な 影響を及ぼす。スペクトルの主要部は Teff と C/O で決まる。計算は マイクロ乱流 3 km/s と 12C/13C = 89 で行われた。 グリッド モデルは Hofner 2003 のグリッドを拡張した。それは、L = 5200, 7000, 10,000 Lo, Teff = 3400, 3200, 3000, 2800, 2600 K, C/O = 1.1, 1.4, P = 295, 390, 525 d で、周期と 光度は P-L 関係で繋がれている。Δup = 2, 4 km/s. 観測星は SRs と Irrs モデルとの比較星は SRs と Irrs で位相が決めにくい。また、モデルは脈動 大気ではなく、ピストン運動を内側境界に置き、フラックス H を一定に仮定 している。その結果、運動学的変化=密度-温度構造、衝撃波の進行、と変光 位相には観測とのズレが生じる。Nowotny04 によると、CN 1.995 μm と CO 第2倍音の速度は、モデルと観測で同じ位相変化を示す。しかし、これらの吸 収線は T > 3000 K 以上という大気の深部で形成される。一方、ここで議論 する低分散スペクトルの主要部は T ≈ 2200 K の大気上層、または星風 基部で形成される。そこでの速度変化はあまり周期的ではない。 |
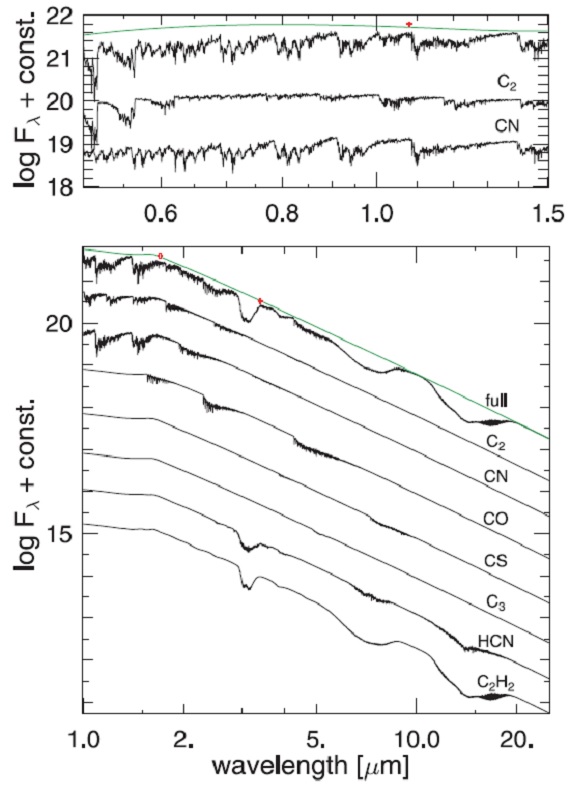 図1.上:モデル l52t32c1 の極小期合成スペクトル。 緑線=連続光。上=合成スペクトル。下二本=C2 と CN の寄与。 下:最上位の黒=合成スペクトル。他は分子の寄与。 |
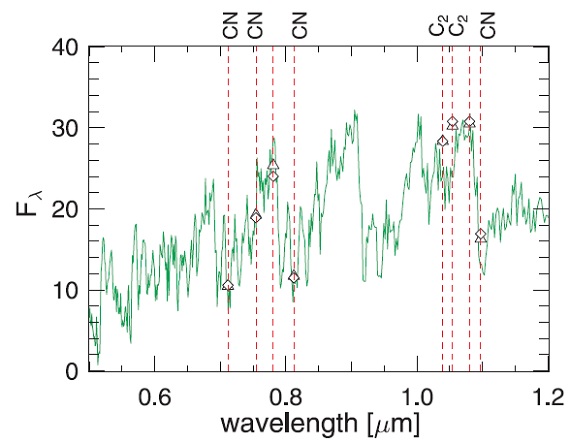 図2.モデル l52t32c11u4 極小期(φ0.5)合成スペクトルとTX Psc の比較。 TX Psc TX Psc は最も明るい炭素星で、 Lb で マスロスは 9.1 10-8 Mo/yr (Olofsson93) である。 観測 観測スペクトルには Baumert 1972 による 2 回の Kuiper Airborn Observatory 観測と 3 SWS/ISO 観測をデータに用いた。モデルスペクトルは T* = 3200 K, L* = 5200 Lo, M* = 1 Mo, C/O = 1.1, P= 295 d, Δup = 4 km/s を用 いた。図2にスペクトルを比較した。観測とモデルは 1.0804 μm で合わせ てある。この波長が連続光水準に最も近いからである。 |
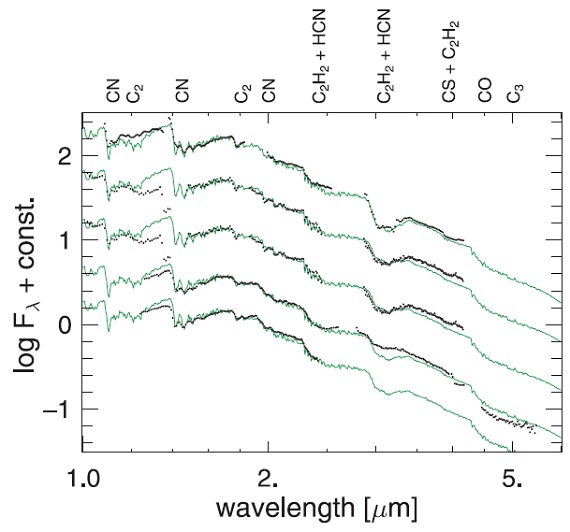 図3.緑= l52t32c11u4 極小期(φ0.5)合成スペクトル。 黒=観測。上から φ 0.83, 0.66, 0.71, 0.71, 0.66. 図3= 1 - 5 μm スペクトル 図3には5つの観測スペクトルをモデルと比べた。1.7 μm が最も薄いので そこで合わせてある。上から三つはフィットが良いが、4つ目の浅い C2H2/HCN 吸収帯ははどの位相の合成スペクトルでも 再現できなかった。CN 1.46 と C2 1.77 μm 帯は良く合い、 Teff (CN から)と C/O (C2 から) は適切であったことを示す。 それら、Teff と C/O, は主に C2H2, HCN, C3 強度から決めた。 |
|
2.4 - 4 μm スペクトル 図4には SWS スペクトルをモデルと比べた。両者は 3.4 μm で合わせてある。 上から一番目から二番目へ 3 μm 帯が深くなっているのは温度の低下を示す。 我々はモデルフィットを 2.5, 3, 3.8 μm C2H2/HCN 帯に集中した。そこでは基本的には光球を見ることになり, l52t32c11u4 モデル はこの波長域を正確に表現するはずである。 5.5 - 7 μm スペクトル 5.5 - 7 μm でのスペクトルの一致は悪い。高温期にはまあまあだが、 低温になると不一致が目立つ。特に 5 μm C3 帯の長波長側が いけない。6 - 8.5 μm での 7 μm より短い側は C2H2 /HCN が、7 μm より長い側は CS が支配的なはずであるが、観測スペクトル では CS の吸収しか見えない。この波長帯では CS は大気の深い部分を見ていて、 上層部は C2H2/HCN の吸収帯が見えるはずである。 我々のモデルは C2H2 吸収帯が強すぎる。これは球対称 静水モデル Gautschy-Loidl01 でも現れた現象である。平面大気(Jorgensen00) ではこの不一致が現れないので、球対称モデルの最外層起源の吸収かも知れない。 まとめ というわけで、まとめると、 TX Psc の観測スペクトルは合成スペクトルで 極めて上手く説明された。 4.2.1.モデルパラメターの影響T*スペクトルフィットで最も重要なパラメターは T* である。TX Psc のベスト フィットは 3200 K で得られたが、100 K 上げただけで C2H2 /HCN 帯はずっと弱くなる。ただ、KAO 観測で見えた弱いC2H2 /HCN 帯を説明するために T* を上げると全体の SED が合わなくなる。 C/O L, M の影響は大きくない。 C/O が高いと、C3 5.1 μm 帯と C2 0.5, 3 μm 帯が強まる。 |
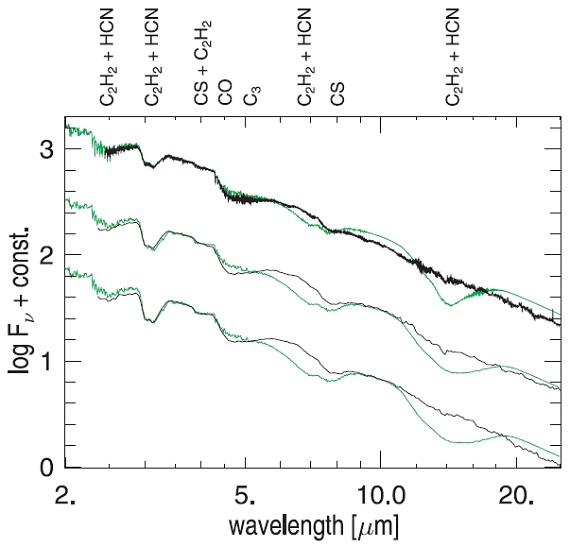 図4.緑= l52t32c11u4 極小期(φ0.5)合成スペクトル。 黒= SWS 観測スペクトル。上から φ 0.66, 0.71, 0.83. 一般に、我々のモデルは C2 1.7 μm 吸収線は上手く説明するが、 1.0395, 1.0544 μm 線は強すぎてしまう。 P 周期 P の変化、例えば、ダストフリーモデルで P を半分にすると、驚くこ とに吸収線強度が強まる。その理由は、浮揚したガスが次々に衝撃波の攻撃 を受け、浮揚物質が多く溜まり、多原子分子の分圧が高まったからであろう。 それが、我々が普通温度の目安に使っている C2H2 /HCN 3, 3.8 μm 帯強度を上げているのだろう。 |
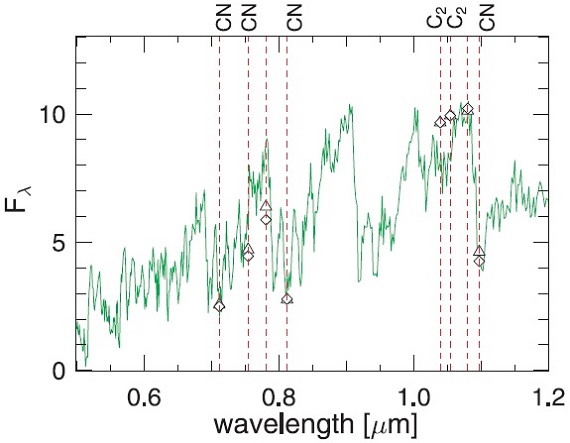 図5.l52t30c05u6pi 極小モデル(φ=0.52) と Baumer 観測 (三角と菱形)との比較。 ベストフィット この星は SRb 型で Schoier, Olofsson 2001 はマスロス= 6.5 10-9 を与えている。ベストフィットは T* = 3000 K, L = 5200 Lo, M* = 1 Mo, C/O = 1.05, P = 186 d, Δup = 6 km/s である。 Baumert 観測 図5にはBaumert 1972 の4回の観測の最大値と最小値をモデルと比較した。 CN 0.7117(Δν=+3), 0.8122(Δν=+2), 1.0975(0, 0) は良く合う が C2 1.0395, 1.0544 μm は強くなりすぎる。 |
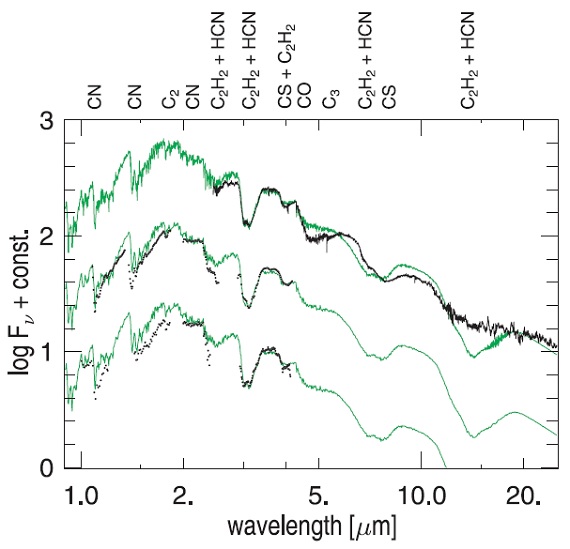 図6.緑線= l52t30c05u6pi 極小モデル(φ=0.52) と黒線=SWS/ISO との比較。モデルは上から φ = 0.83, 0.89, 0.83. SWS/ISO 図6には SWS/ISO スペクトルとの比較を示す。モデルは C2H2/HCN 3, 3.8 μm 帯強度と形を上手く再現する。 しかし、 4.5 μm から先がまずい。モデルの CO 4.6 μm 帯は弱すぎた。 逆に、C2H2 6 - 7 μm 帯と CN 8 μm 帯は強す ぎる。 |
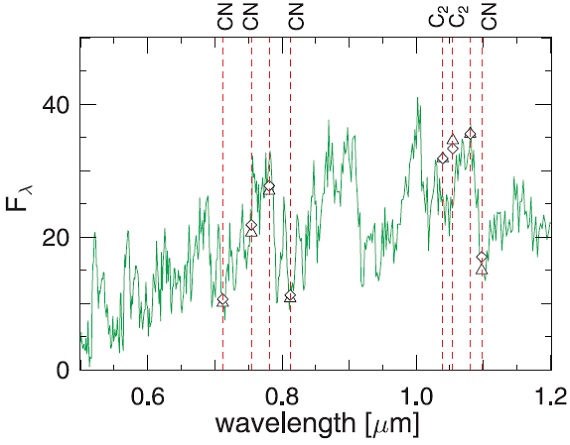 図7.l52t34c12u2p モデルと V460 Cyg Baumert72 狭帯フィルター測光との比較。 三角=最高カラー。ひし形=最低カラー。 星の性質 Schoier, Olofsson 2001 はマスロス= 1.8 10-7 を与えている。ベストフィットは T* = 3400 K, L = 5200 Lo, M* = 1 Mo, C/O = 1.2, P = 148 d, Δup = 2 km/s である。 Baimert 1972 の狭帯測光 図7に Baimert 1972 の狭帯測光との比較を示す。モデルの 1.0395, 1.0544 μm 吸収強度は強すぎる。 SWS スペクトル SWS とは 2.4 - 4.6 μm で正しくフィットできた。2.5 μm より短い側 と 6 μm より長い側では、モデルが星風、ダストなしであることが原因である。 C3 5.1 μm は上手く合う。 C2H2 7 μm 帯は強すぎる。 |
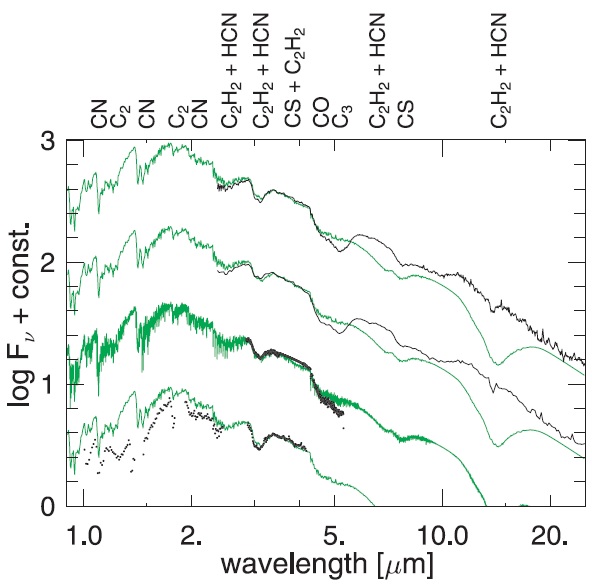 図8.l52t34c12u2p モデルと V460 Cyg SWS/ISO スペクトル。変光 位相は上から φ = 0.54, 0.56, 0.56, 0.57. 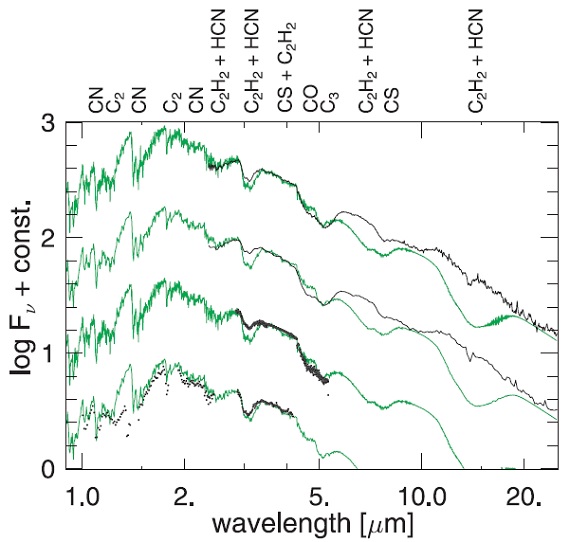 図9.l52t34c14u4pim15 モデル φ = 0.55 と V460 Cyg SWS/ISO スペクトル。 |
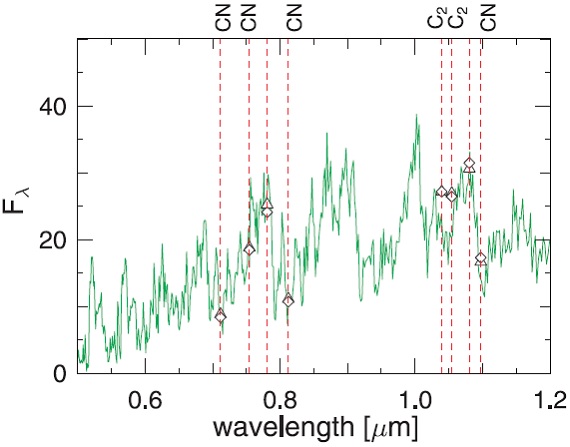 図10.l52t30c20u2pm20 モデルと T Lyr Baumert72 狭帯フィルター測光との比較。 三角=最高カラー。ひし形=最低カラー。 星の性質 Schoier, Olofsson 2001 はマスロス= 7.0 10-8 を与えている。ベストフィットは T* = 3000 K, L = 5200 Lo, M* = 2 Mo, C/O = 2.0, P = 148 d, Δup = 2 km/s である。 Baimert 1972 の狭帯測光 図10に Baimert 1972 の狭帯測光との比較を示す。モデルの 1.0395, 1.0544 μm 吸収強度は強すぎる。 SWS スペクトル T Lyr は強い C2 1 - 2 μm バンド、 C2H2/HCN 3, 7 μm 帯 を持つ。SiC 放射帯 11 μm はない。フイットは上手く行っていない。 C2H2/HCN 2.5, 3 μm 帯は良く合う。 |
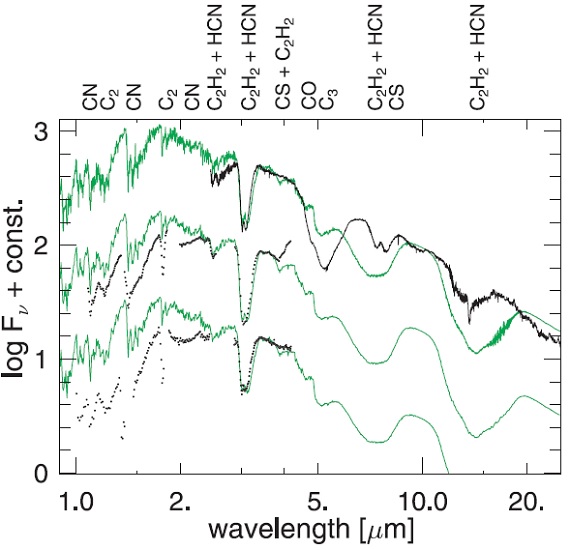 図11.l52t30c20u2pm20 モデルと V460 Cyg SWS/ISO スペクトル。変光 位相は上から φ = 0.61, 0.52, 0.09. 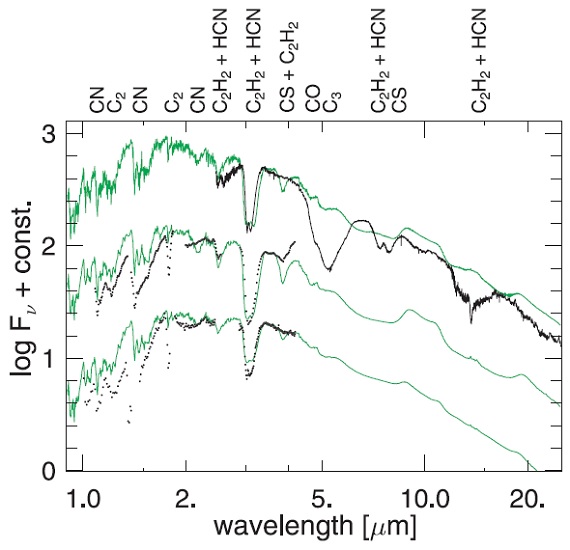 図12.l70t28c16u4 モデル φ = 0.509, 0.82 と0.00 |
|
星風ナシモデル 今のところ、動力学モデルは主に星風ナシで、比較的高温の星に向いている。 それらは標準的な静水モデルと比較され、またそれらの穏やかな変動を説明する ために用いられた。 ダストの性質 星風モデルの計算に当たってはダストの性質を注意深く調べなければならない。 Andesen03 はダストの性質が星風速度、凝結度、マスロスに大きく影響することを 指摘した。ここでは Rouleau, Martin 1991 の非晶質炭素の光学的性質とグラ ファイトの密度 2.25 g/cm3 を採用する。 二つだけ 今回は二点の検討に限る。 5.1.S Cep星風モデルの目的表2に S Cep の基本性質が載っている。ここでは、フィットを目的とする のではなく、星風モデルによる一般的な傾向を調べることを注意する。 図13にモデルスペクトルと KAO, ISO スペクトルとを比較する。 分子帯の再現度 S Cep の 5 μm よち長波長側では C2H2/HCN 7, 14 μm 吸収帯と 11 μm SiC 放射 帯がある。星温度の決定は C2H2/HCN 2.5, 3, 3.8 μm 吸収帯強度と全体の SED が良くフィットされるという条件で決める。明らかにこの条件は幾つかの位相、 特に 2H2/HCN 3 μm 吸収帯が強い時期には満たされ ない。SED と 2.3 μm スペクトル、3.8 μm 2H2/HCN 吸収帯がフィットする時には、強い 2H2/HCN 3 μm 吸収帯と CO 4.6 μm 帯、 C3 5.1 μm 帯を再現できない。 C2H2/HCN 3, 3.8 μm 吸収帯の位相変化 C2H2/HCN 3, 3.8 μm 吸収帯は φ 0.56 = 変光曲線が極大から極小へ向かう半道、で最強になり、可視極小時 φ0.4 (あれ、何か変! ) に最弱になるが、モデルでは極小時に最強となり、極大直前 φ 0.89 に 最弱となる。しかし、 Nowotny04 は同じモデルで CO, CN のラインプロファ イル変化が観測と合うことを見出した。 C2H2 吸収線だけが 大気の上層で形成され、星風領域は位相がずれるのである。 図4, 6, 8, 11 を図 13 と比べるとマスロスの結果次の状況が生じると 判る。 (i)C2H2/HCN 3, 3.8 μm 吸収帯は非常に弱くなる。 (ii)CO 4.6 μm, C3 5.1 μm, それに光球で形成される C2H2と HCN 7, 14 μm 吸収帯はダスト放射で埋まる。 (iii)SED 極大は長波長側に移る |
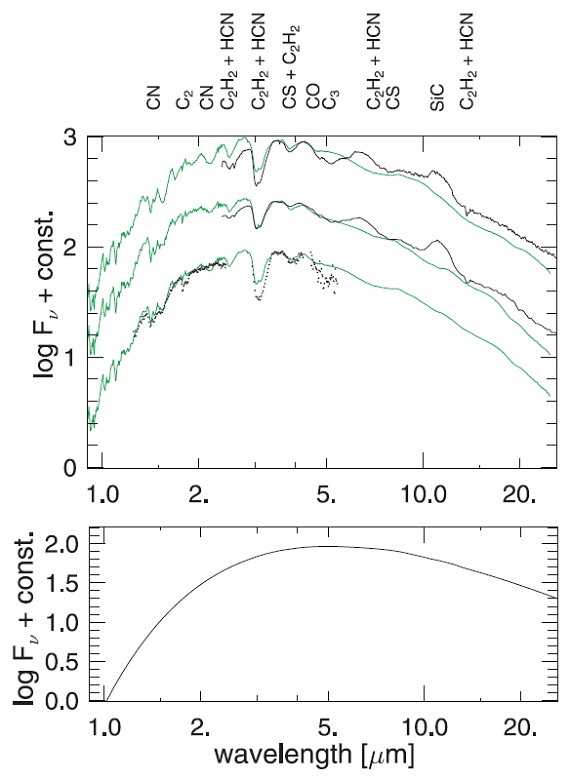 図13.上:緑線=l10t26c14u4f20pi モデル。黒線=上から φ 0.0, 0.4, 0.56. 下:純粋なダストスペクトル (φ 0.56)。 埋め立て 図13のモデルスペクトルは、光球起源の C2H2/HCN 7, 14 μm 吸収帯が殆ど見えなくなっているのに、 C2H2/HCN 3 μm 吸収帯が強いままでいるかを説明できた 最初の例である。その根底にはマスロスを起こす星風がある。マスロスが起きると、 吸収を起こす同じプロセスが C2H2/HCN 7, 14 μm では放射となって働くのである。 (LTE の源泉関数をプランクとすると、 C2H2 とダストは同じ光学的深星風層を見ることに なるけど? ) |
5.2.低温炭素星における 1.53 μm 吸収帯星風合成スペクトル星風モデル l70t28c14u5 の極小付近では 1.53 μm に非常に強い吸収が 出現する。図14にはその拡大スペクトルを示す。 観測スペクトル 1.53 μm 吸収帯は R Lep のような低温炭素星のいくつかで観測されている。 これは C2H 説とC2H2/HCN 説がある。 |
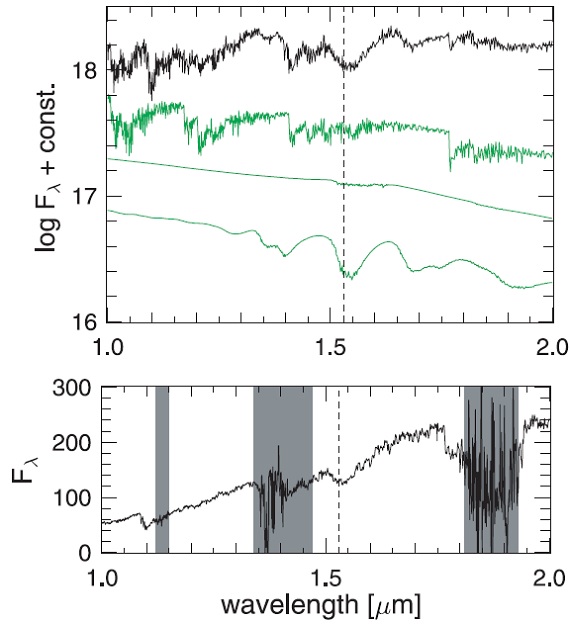 図14.上:黒=星風モデル l70t28c14u5 の極小付近合成スペクトル。 緑線は上=C2, 中=HCN, 下=C2H2. 縦点線= 1.53 μm 吸収帯の短波長端。 下:R Lep スペクトル。網部は大気吸収。 |
|
深く幅広な 14 μm 吸収の予想 平面平行静水モデル、球対称静水モデル、星風ナシ動力学モデルのどれもが 14 μm に深くて幅広な C2H2/HCN バンドを予想した。 しかし、観測スペクトルはどれも弱くて幅が狭かった。もしバンドが光球下部で 形成されるなら、多くの遷移が関与して、幅が広くなるはずである。したがって、 観測されているのは純粋な光球スペクトルではあり得ない。 暖かな分子層 Tsuji97, Yamamura99 は「暖かな分子層」を想定し、その温度と密度を調整 してこの矛盾を解こうと試みた。この案の問題点は、 (1) 背景となる物理モデルの不在 (2) 説明しても星への追加情報がゼロ (3) 3 μm と 14 μm の遷移確率と振動準位の励起エネルギーがほぼ等しい。 したがって、14 μm バンドを弱めようとして温度逆転を導入すると、3 &mu:m バンドも弱くなる。 部分的「分子層」 Jorgensen00 は 500 K の「分子層」を部分的に光球の上において、強い 3 μm 帯と弱くて鋭い 14 μm 帯を両立させようとした。しかし、物理的 基礎を欠くという問題が残る。 |
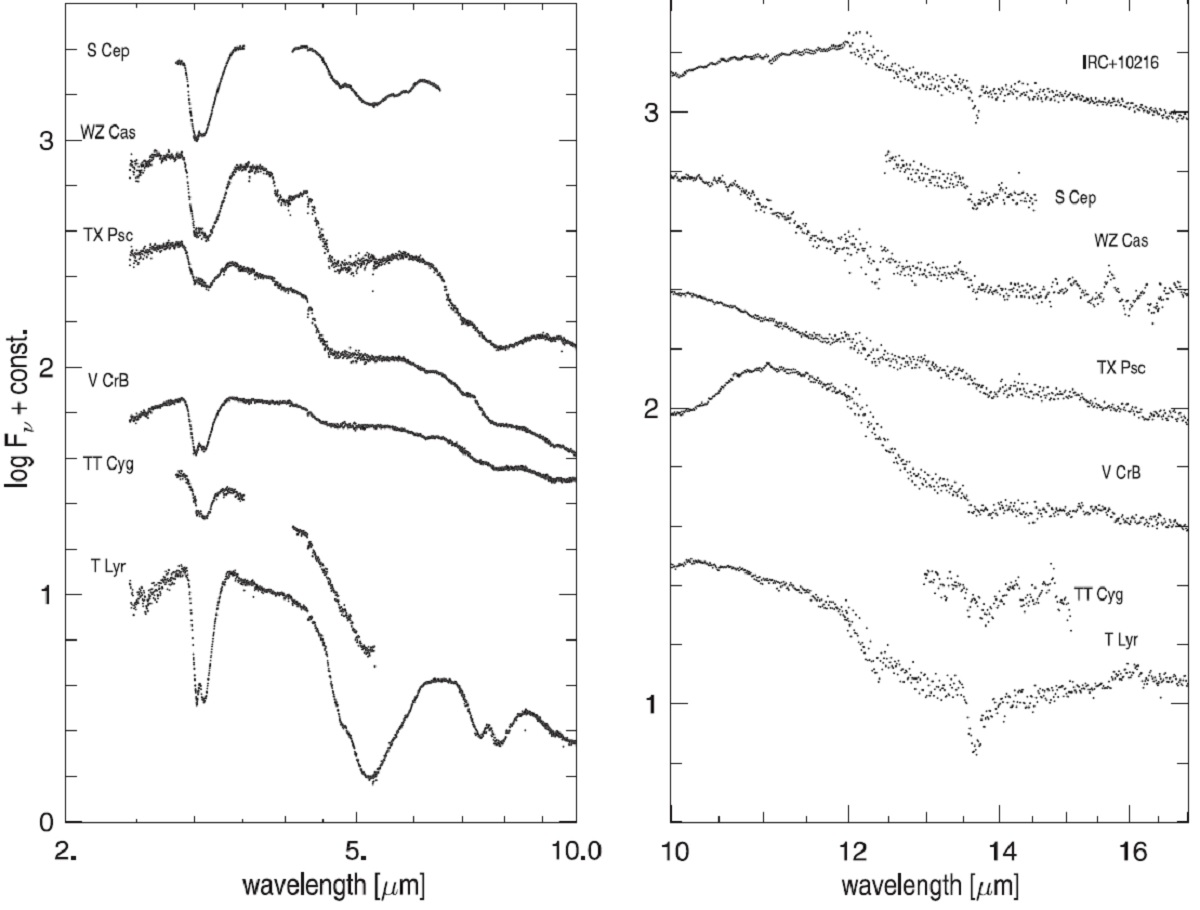
動力学星風モデル 我々の動力学モデルでは、上層のダストと C2H2, HCN からの放射が光球吸収帯を埋め、見える吸収帯は13.7 μm C2H2 と 14 μm HCN 基幹部のみとなる。 (埋めるって、やに感覚的。結局 光学的に厚い上層部=星風下部?の温度勾配が新たに MIR 吸収線を作る、つまり 光球は見えず星風のスペクトルを見ているということか? ) l70t28c16u4 は興味ある遷移モデルである。図12を見ると、上の合成スペク トルで 14 μm 帯のウイングは依然として吸収を示し、一方 13.5 - 14 μm の「中心部」は強い放射に変わっている。次に中のスペクトルでは放射の寄与は 小さいがまだ見える。下では全吸収帯が放射で埋められ、なんのバンドも見え ない。 炭素星 SWS 図15には 3 と 14 μm 帯が観測された炭素星 SWS スペクトルを集めた。 Aoki99 は TX Psc, V CrB, SS Vir を調べている。スペクトルを調べた結果、 彼らが同定した以外の輝線が S Cep, WZ Cas, TX Psc, TT Cyg で見つかった。 T Lyr 我々のサンプル中 T Lyr のみが深い 14 μm 吸収を示す。この他にも 3, 5.1, 7, 8 μm で強い吸収を持つ。それらは C2H2, HCN 起源である。 |
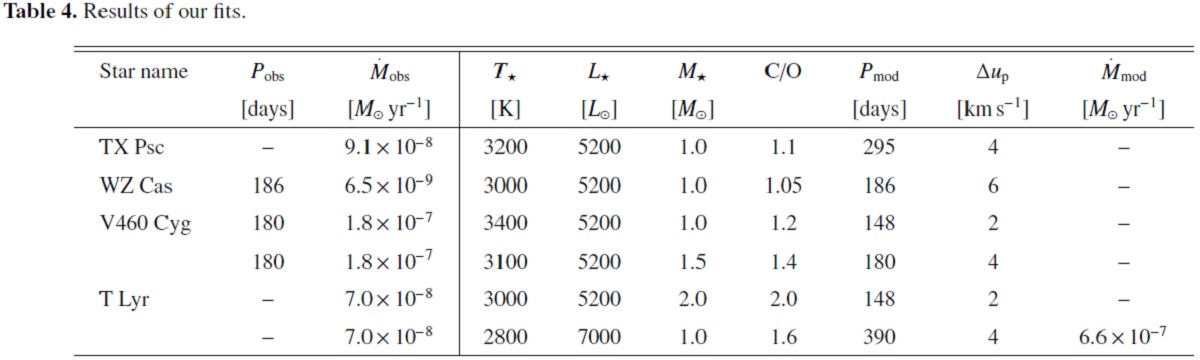
| 今回初めて、炭素星観測スペクトルと星風背ペクトルとの比較が行われた。 |