2.1.一般特性
2.2.流体方程式
流体力学方程式を時間依存で解く。2.3.輻射方程式
流体の配置が決まったら、その配置に対する輻射の分布を解く。2.4.結果の定義
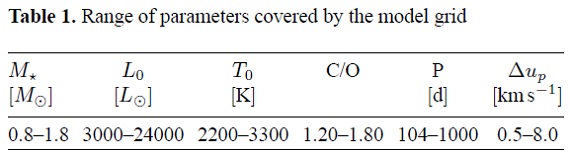
表1.モデルグリッドの範囲
| ダスト形成を含めた時間依存流体方程式を解き、マスロスを調べた。モデル グリッドは二つの領域に分かれた。(A) 領域は、5 km/s を超す星風領域である。 星風はダストに働く輻射圧で駆動される。 |
(B)領域では、星風速度は小さく、
マスロス率は 3 10-7 Mo/yr を越えない。輻射圧の役割は副次的で
ある。(A) から(B) への転換は急である。
(表2がない?) |
|
マスロス下限値 Epchtein, Le Bertre, Lepine, Marques dos Santos, Matsuura, Picazzio (1987), van der Veen, Habing (1988) は IRAS 二色図のギャップを星風が安定して存在できるのは、マスロス率が 数 10-8 Mo/yr 以上の場合であると予想した。それは理論モデル の結果とも一致する。 超低マスロス星 Chan, Roelig, Onaka, Yamamura, Tanabe (1998) はバルジの MIR 拡散光スペクトルがマスロス星のそれと似ていることから、 多数の低光度マスロス星の存在を予想した。一方、 Omont, Ganesh, Alard et al. (1999) は 10-9 Mo/yr の非常に低いマスロス率の星をやはりバルジに見出 した。 |
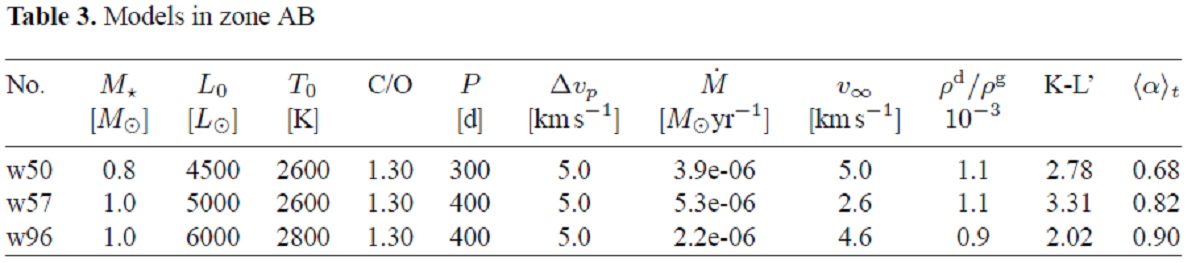
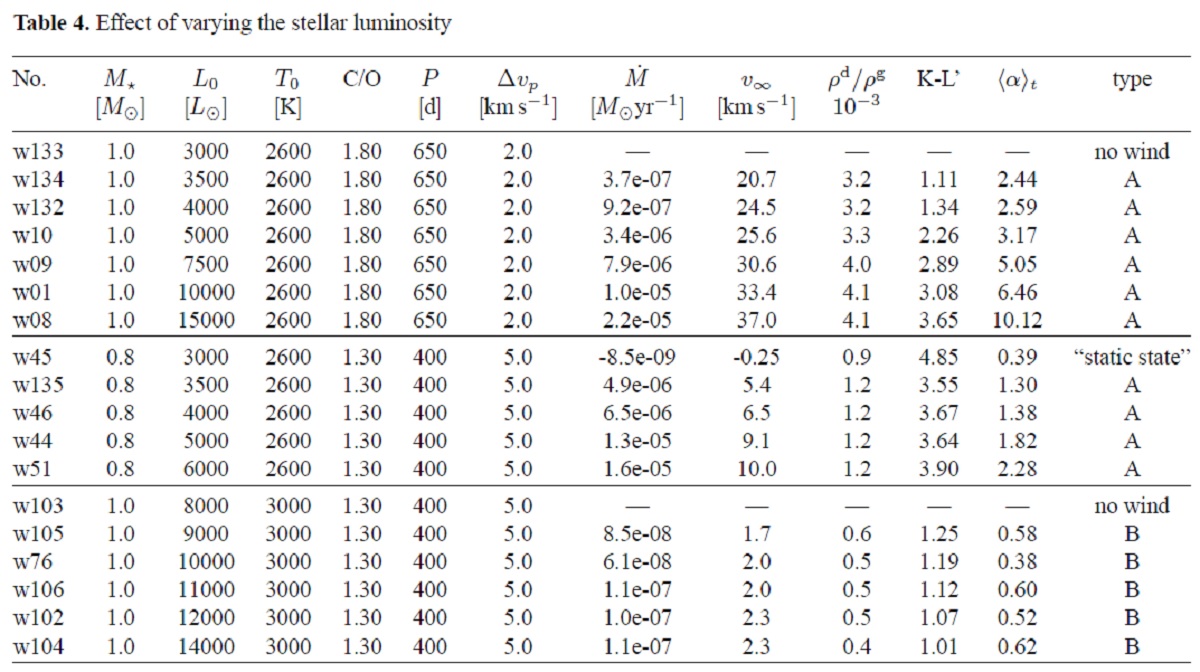
AGB が IS ダストの 70 % Sedlmayr 1994 は星間空間への質量供給において AGB 星の寄与が 70 % に 達するとした。 ダスト形成付きの」流体モデル Le Bertre, Winters 1998 はカラーとマスロス率の間に関係があることを見出した。 そこで、本論文では TU-Berlin モデル(Fleischer92)=ダストはKoike 炭素データ 使用で、ダスト形成をモデルに入れ、輻射圧はダスト量に比例、を使い 様々なパラメターで計算。主に炭素質ダスト、ちょこっとシリケイト。 |
2.1.一般特性2.2.流体方程式流体力学方程式を時間依存で解く。2.3.輻射方程式流体の配置が決まったら、その配置に対する輻射の分布を解く。2.4.結果の定義 |
 表1.モデルグリッドの範囲 |
3.1.マスロスとカラーの関係図1.モデル全体での (dM/dt) - (K-L) 関係。ダストは Pleibisch93 の非晶炭素。 |
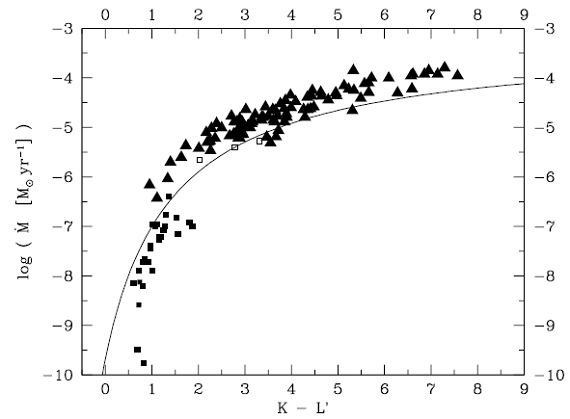 |
3.2.輻射加速度 α の影響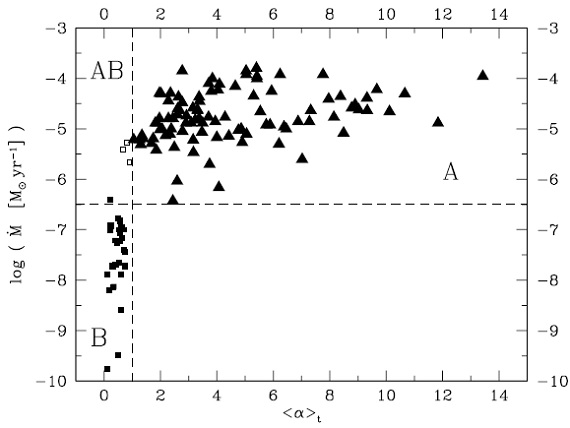 図2.(dM/dt) - 輻射加速 α 関係。ダストは Pleibisch93 の非晶炭素。 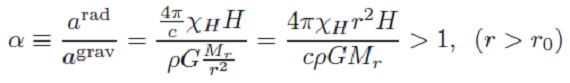 もし、 r2H = L*/16π2 を仮定すると、  α > 1 の条件をエディントン光度 Ledd で書き直すと、 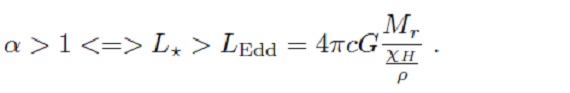 α の時間平均は、 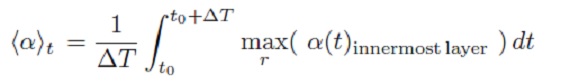 図2を見ると、⟨α⟩ < 1 でのマスロス低下は明らか。 領域Aでは輻射加速が効いている。領域Bでは輻射加速が効いていない。 しかし領域ABには ⟨α⟩ < 1 だが、 (dM/dt) > 10-6Mo/yr のモデルがある。これらはマスロス率 と α が振動するモデルである。 |
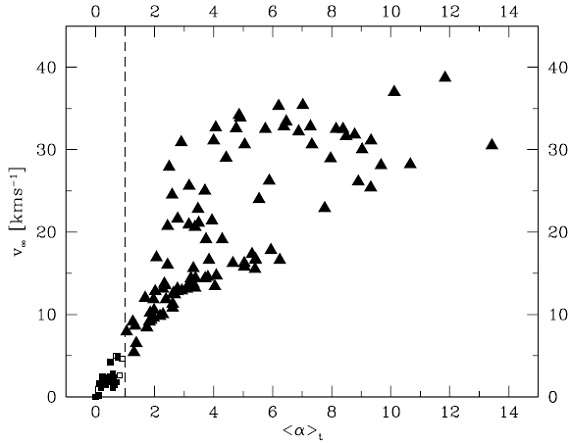 図3.終端速度と輻射加速度の関係。ダストは Pleibisch93 の非晶炭素。 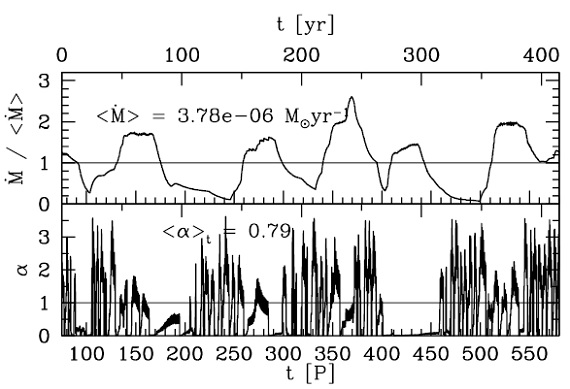 図4.ABモデルの振動する (dM/dt) と α. IRC+10216, CRL2688 などで観測される多重シェルとの関係が興味深い。 |
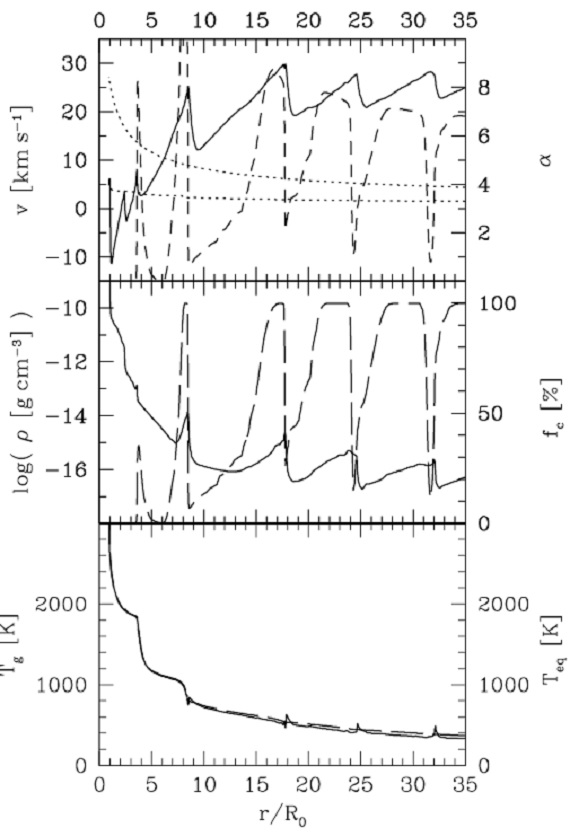 図5.A モデルの動径構造の例。 上:実線=速度。破線=輻射加速度/重力加速度。 上側点線=脱出速度。下側点線=音速。 中:実線=密度。破線=固体化率。 下:実線=ガス温度。破線=平衡温度。 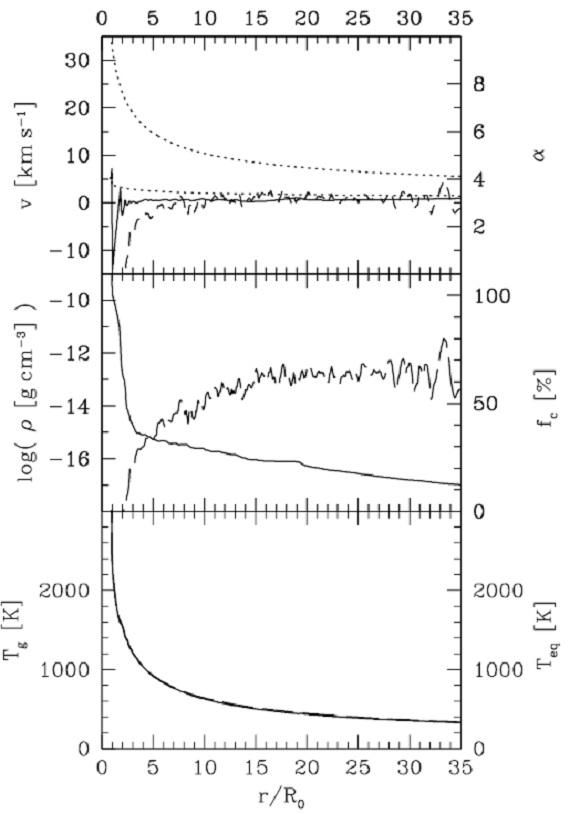 図7.B モデルの動径構造の例。線の意味は図5と同じ。 |
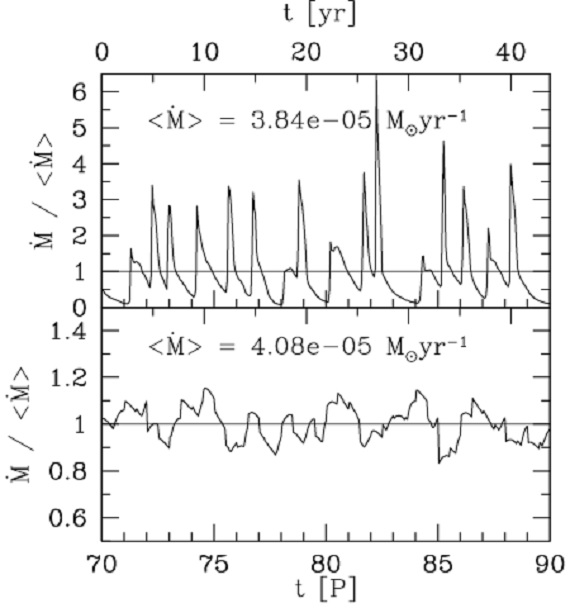 図6.Aモデルでのマスロス率時間変化の例。上:r=45 Ro における マス流出率。下:動径平均マスロス率の時間変化。上と下との横軸 スケールの違いに注意。 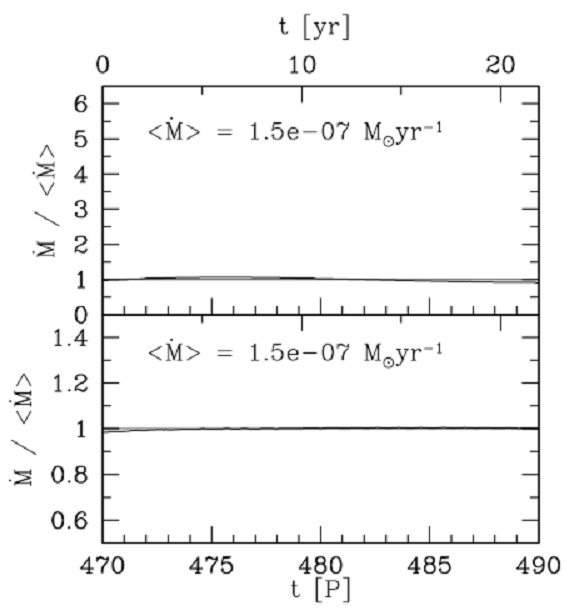 図8.Bモデルでのマスロス率時間変化の例。線の意味は図6と同じ。 線の意味は図5と同じ。 |
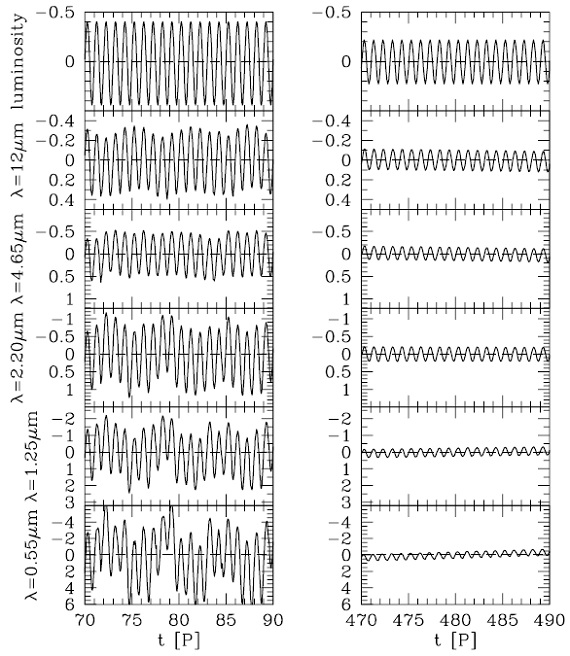 図9.様々な波長での変光。左=A, 右=B.一番上が L 変化。 |
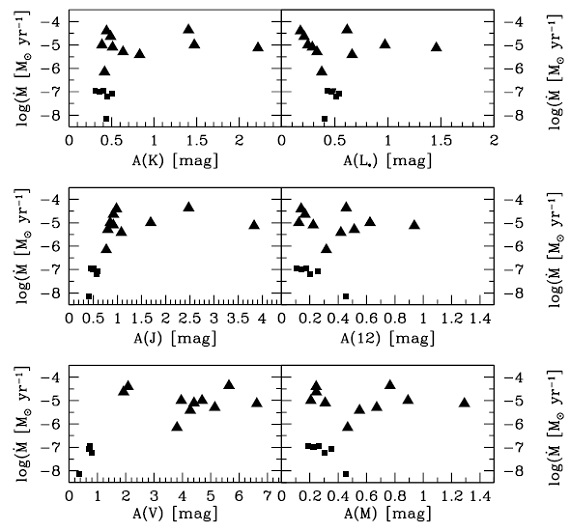 図10.16個のモデルに対するマスロス率と変光振幅 A の関係。 |
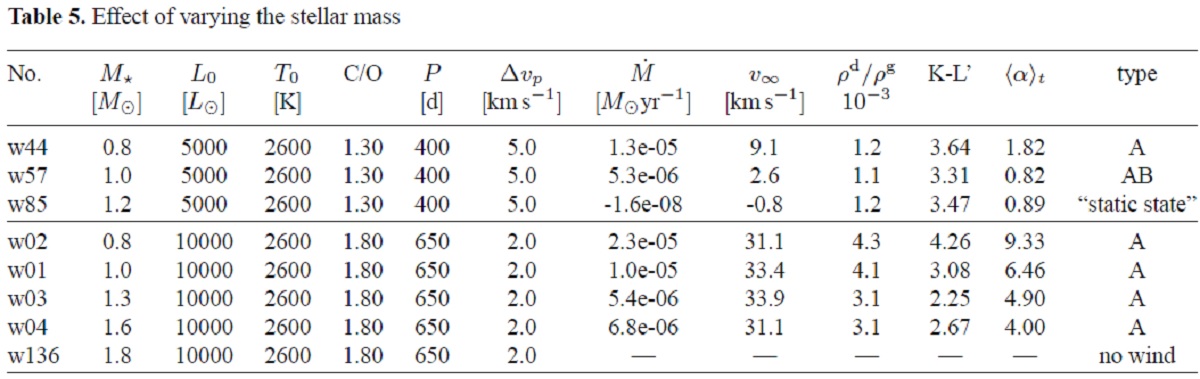
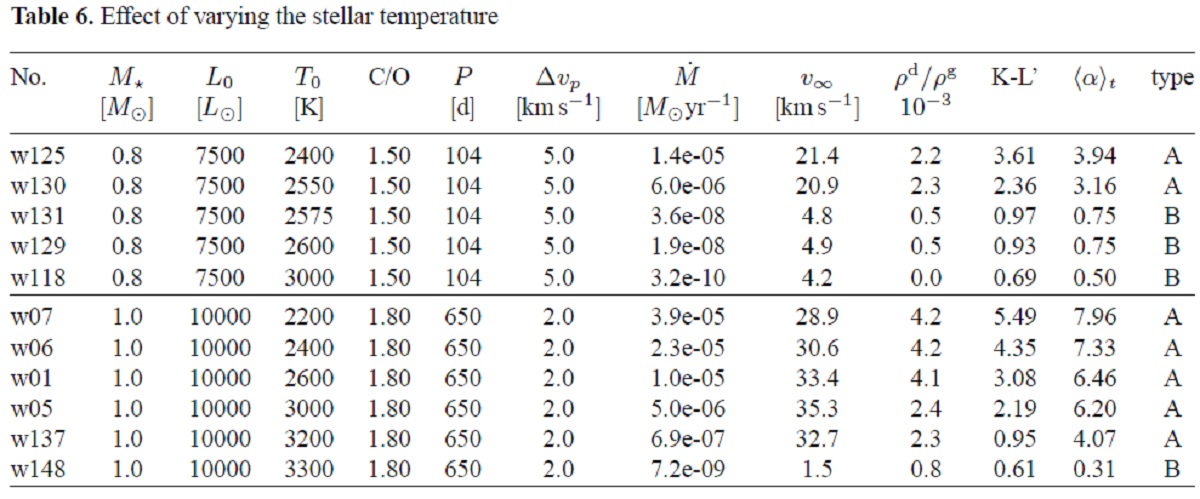
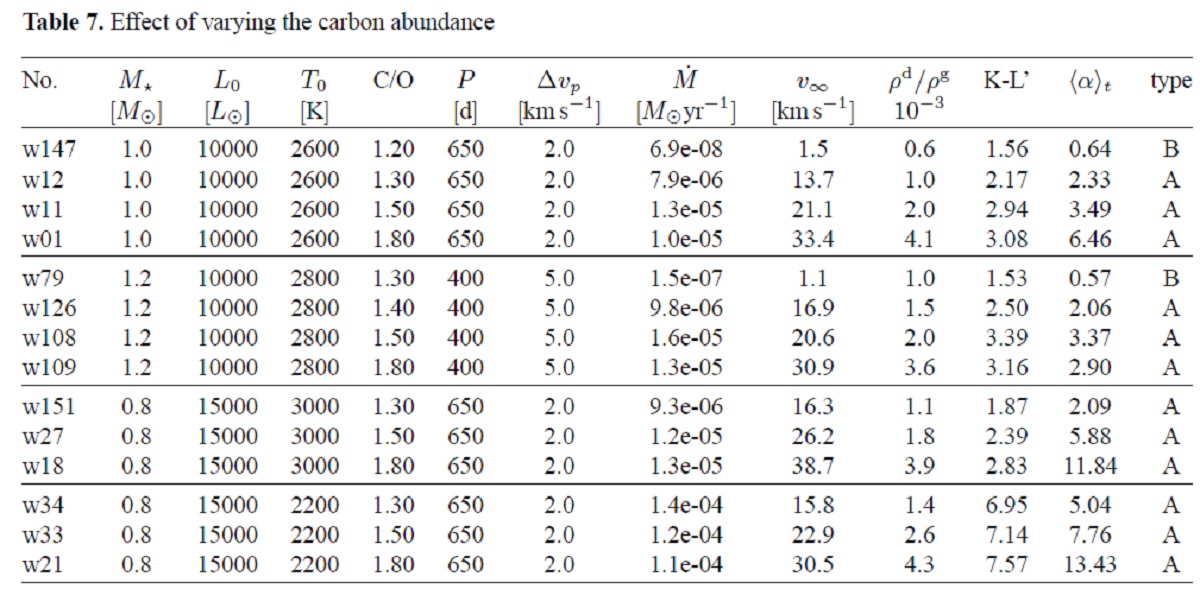
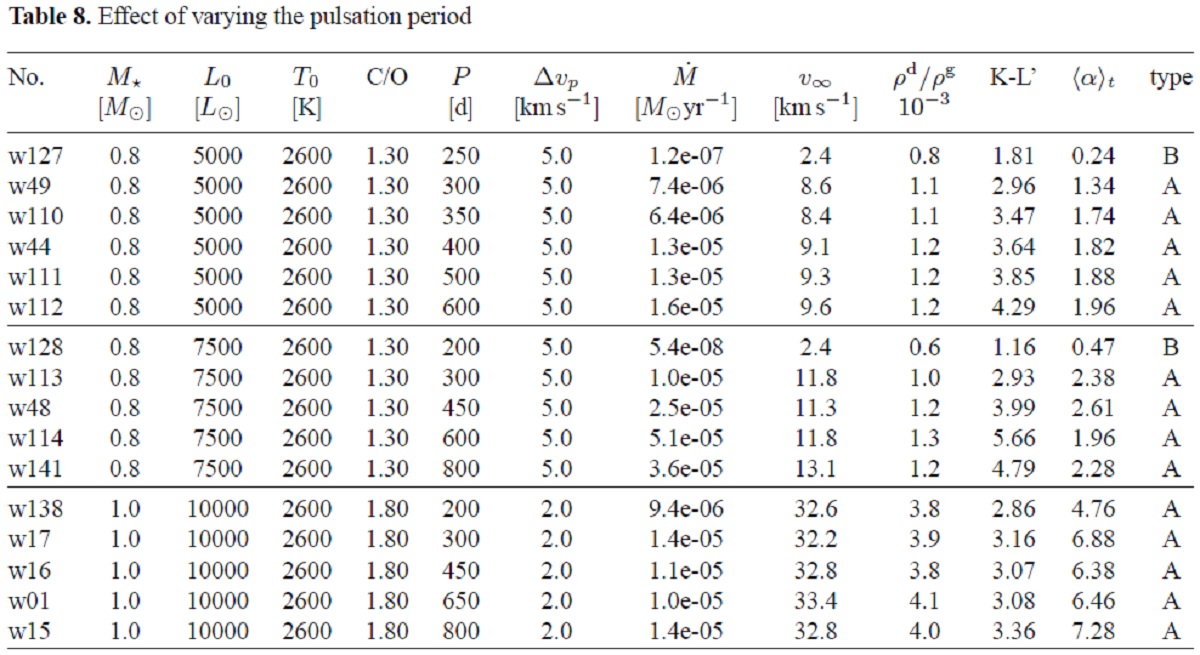
3.5.1.光度の影響3.5.2.星質量の影響3.5.3.光度と質量の結合効果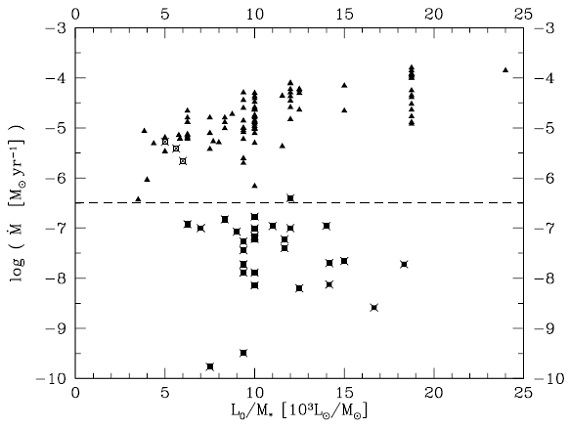 図11.(dM/dt)と Lo/Mo の関係。 |
3.5.4.恒星温度の影響3.5.5.炭素量の影響3.5.6.周期の影響 |
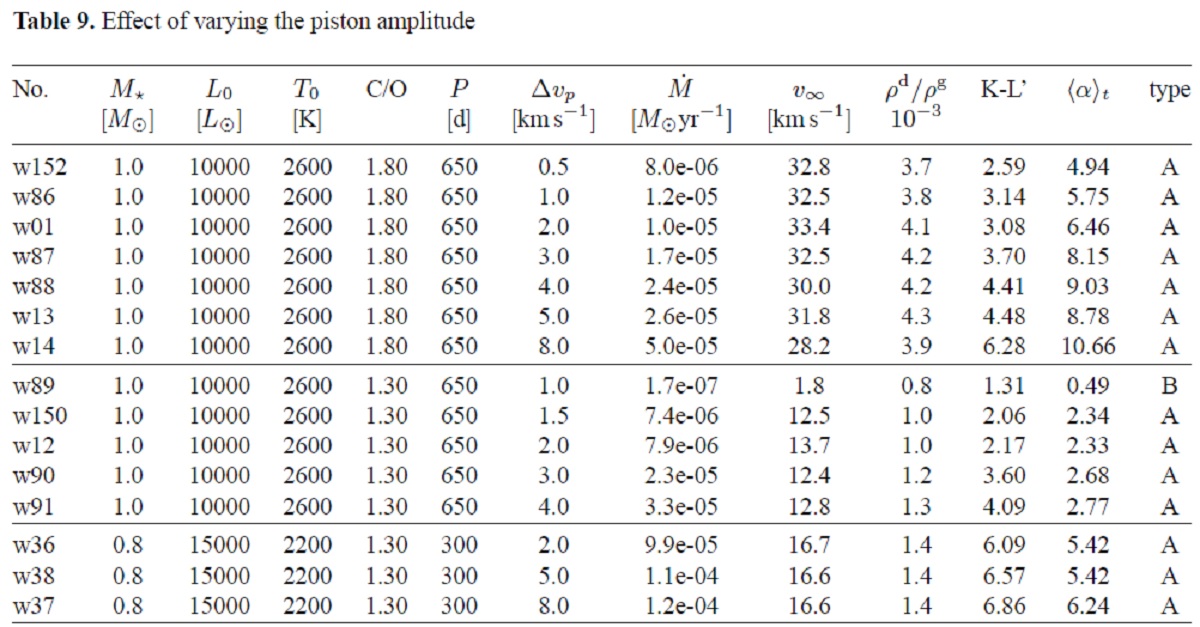
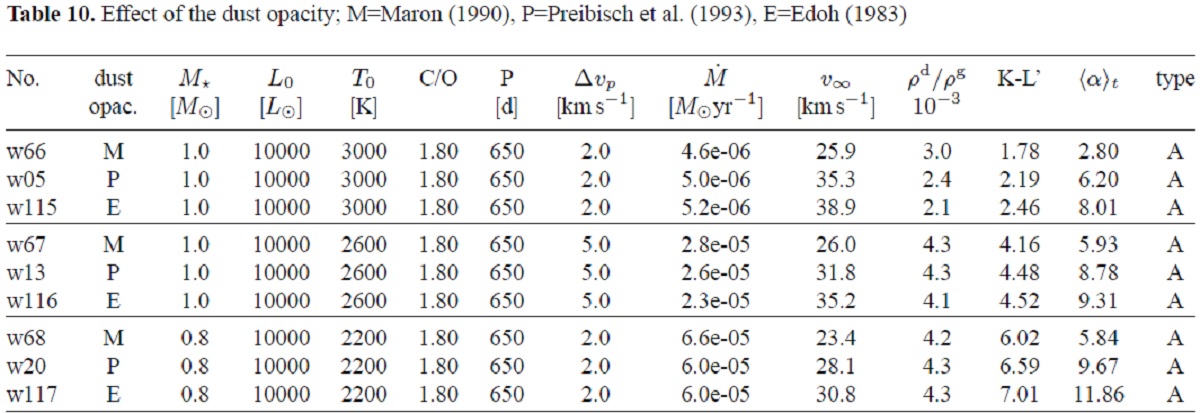
3.5.7.ピストン振幅の影響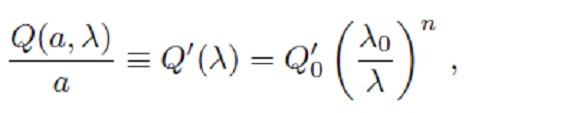
|
3.6.オパシティの効果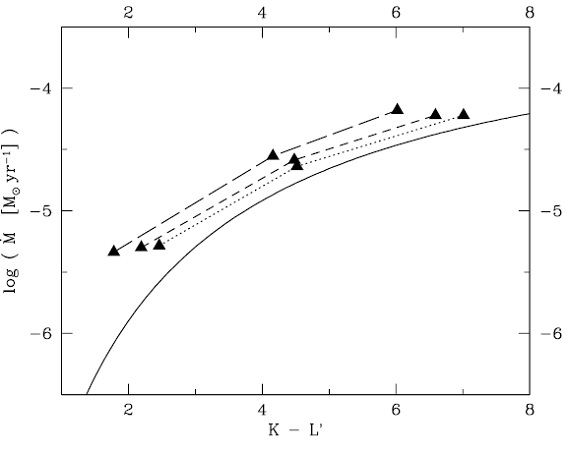 図12.3つのモデルでの(dM/dt)と (K-L') の関係。 長破線=Maron90, 短破線= Preibisch93, 点線=Edoh83. |
3.7.カラーとマスロス率の関係の意味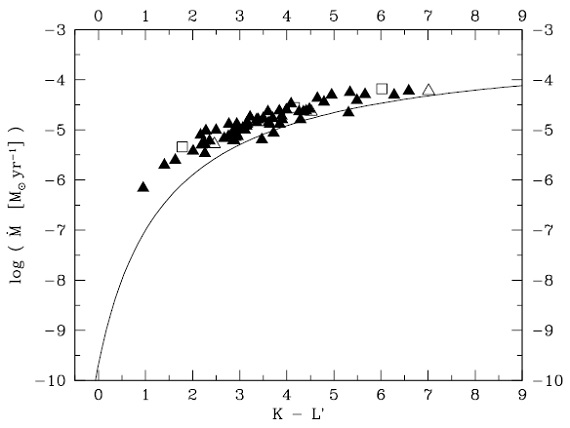 図13.A 領域モデルに対する (dM/dt) - (K-L') 関係。 3.8.低速星風 |
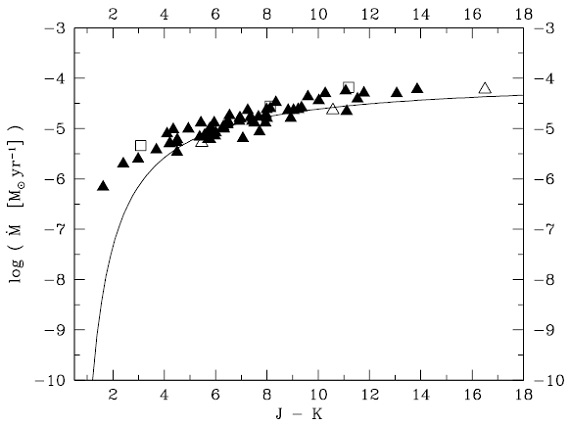 図14.A 領域モデルに対する (dM/dt) - (J-K) 関係。 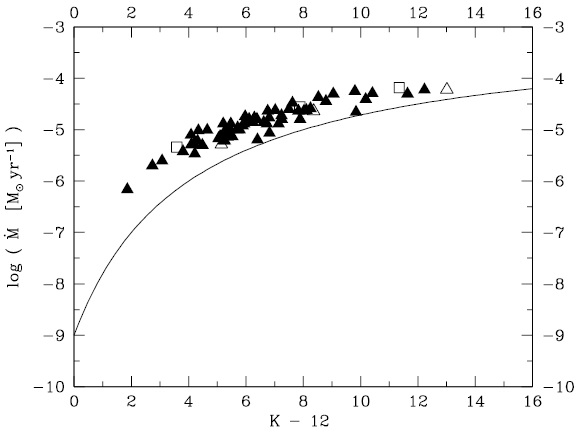 図15.A 領域モデルに対する (dM/dt) - (K-12) 関係。 |
4.1.ガスオパシティ4.2.O-リッチモデルB 領域モデルが Chan, Roelig, Onaka, Yamamura, Tanabe (1998) Omont, Ganesh, Alard et al. (1999) の説明になる可能性がある。 |
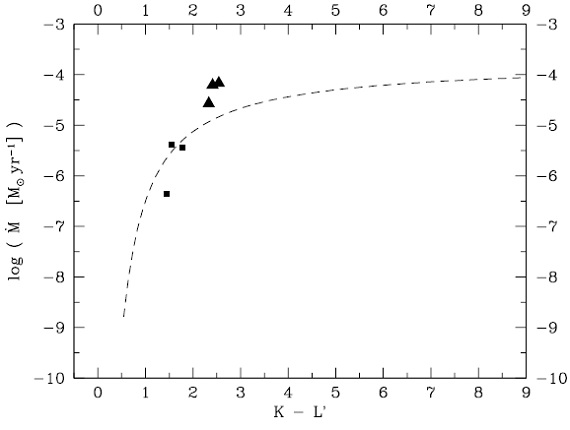 図16.O-リッチモデルの (dM/dt)-(K-L') 関係。Draine-Lee "astronomical silicate" モデル。 Draine, Lee (1984), Draine (1985) |