On the Deprojection of the Galactic Bulge


Binney, Gerhard
1996 MN 279, 1005 - 1010



　アブストラクト

　銀河系バルジの測光観測において起きた問題を解決するためのアルゴリズム を開発した。バルジは天空上にある大きさで広がっている。これにより空に 投影された二次元輝度分布を、バルジが３つの直交する対称面を持つという 仮定の下で、３次元分布に戻すことが可能である。

　１．イントロダクション　

３次元分布を一意に決められるのか？　
　DIRBE/COBE はデータの質が高く、現在幾つかのグループがバルジモデルを 作っている。そこから疑問が起きた：
投影輝度分布から放射密度の３次元分布を一意に決められるのか？

対称面の仮定　
　一般的には２次元輝度分布から３次元放射分布に戻すこと一意性の保証はない。 しかし、適当な対称性を仮定するとそれが可能となる。３枚の直交する対称面を バルジが持つと仮定し、その方向をどう定めるかのアルゴリズムをここで提案する。
( ３次元分布を関数展開して、各関数の ２次元投影関数を決め、空の輝度分布をその投影関数で分解したら？)

　２．リチャードソン・ルーシーのアルゴリズム　

　２．１．動機　

　遠方銀河では視線同士が平行で、視線に沿って物体を動かし、様々な ３次元分布を得る自由度が高い。しかし、バルジのように有限視角を持つ 天体ではその自由度が限られる。

　２．２．数学的定式化　

　座標軸　

　バルジの主軸と一致する座標軸を取る。それら３軸は３つの対称面の交線 である。任意の x に対し、同じ放射密度 ν(x) を持つ８点、xi, i = 1, 2, ..., 8 が存在する。

　表面輝度　I(Ω) と放射密度 ν(x)　

　　　ν(x) = ∫+octant d3x′ δ8(x, x′)ν(x′) 　　　　　 　　　　（１）
ここに、δ8(x, x′) = δ(|x1|-x1′) δ(|x2|-x2′) δ(|x3|-x3′)　　（２）

　太陽からの方向 Ω の表面輝度は

　　　I(Ω) = ∫ds ν(x(s))　　　　　　　　 　　　　　　　　　　　　（３）
ここに、x(s) = xo + sΩ

(1) 式を (3) に代入して、
　　　I(Ω) = ∫+octantd3x′ ν(x′)∫ds δ8(x, x′)
　　　　　　= ∫+octantd3x′ ν(x′)K(Ω | x′)　　　　　　　　　　　（４a)
ここに、K(Ω | x′) = ∫ds δ8 (x(s), x′)　である。
このカーネル K は積分しての規格化は１でなく、

　　　∫d2ΩK(Ω | x′) = ∫d2Ω∫dsδ8 (x, x′)
　　　　　　　　　　　　　　=∫d3xδ8 (x, x′)/s2(x)
　　　　　　　　　　　　　　　　　= 0　　　　　 (x′が＋八分区にない時）
　　　　　　　　　　　　　　　　　= Σi=18[1/s2 (xi′)] = 1/⟨s2(x′)⟩　（ある時）

(8 倍しないでいいのか？ )
　ここに、xi′ は x′ の i-th 対称位置で、 s(x′)=|x′-xo| は太陽と x′ との 間の距離である。(4) 式を考え、次の定義を成す：

　　　　　K′(Ω | x′) =　 ⟨s2(x′)⟩ K(Ω | x′) 　　　　　　　　　　（５）
　　　　　ν′(x′) = ν(x′) /⟨s2(x′)⟩

　明らかに、K′(Ω | x) は方向 Ω が xi のどれか一つを向いていないとゼロである。そして、その方向に向いている ときには、K′ はデルタ関数的になる。 		K′ を Ωi の周りの小さな立体角 ΔΩi で積分すると、

　∫ΔΩi d2ΩK′ (Ω | x′)
　　　　　　　= ⟨s2(x′)⟩ ∫ΔΩi d2ΩK(Ω | x′)
　　　　　　　= ⟨s2(x′)⟩ ∫ΔΩi d2Ω ∫dsδ8(x(s), x′)
=⟨s2(x′)⟩ ∫∫ d2Ωs2ds δ8(x(s), x′)
ΔΩi s2(xi)

= ⟨s2(x′)⟩
s2(xi)

= 1 = 1/8
(Σj=18 1/s2( xj′))s2(xi′)


そこで、
　　　K′(Ω | x) = ⟨s2(x′)⟩ (x)Σi=18δ(Ω-Ωi)/ s2(xi)　（x +octan内)
　　　　　　　　　　= 0 　　　　　　　　　　　　　　　　　　　　　（ない時）　（６）

　リチャードソン・ルーシー近似　

　結論として（３）式の逆変換は、

Ir(Ω) = ∫d3x νr(x)′ K′(Ω | x)
　　　　 = ∫d3x νr(x)K(Ω | x)
　　　　 = ∫ dsνr(x(s))

νr+1(x(s))′= νr(x(s))′ ∫d2Ω K′(Ω | x) [ I(Ω) / Ir(Ω)]
= νr(x(s))′ ∫d2Ω⟨s2(x)⟩ Σ 8 δ(Ω - Ωi) I(Ω)
i=1 s2(xi) Ir(Ω)


単純な形で書くと、

νr+1(x) = νr(x) s2(x) Σ 8 I(Ωi) 1
i=1 Ir(Ωi) s2(xi)


　R-L 法では I(Ω) の代わりに g(Ω)I(Ω)、 ここに g(Ω) は 何でも良い正関数、を使うと収束が良いことが知られている。
(このあたりから理解できない。 )
新しいシステムで得られる逐次近似式 Ir は I ln Ir の代わりに gI ln gIr を極大にする。式 4a の両辺に g を掛けると、新しいシステムでは カーネルが g K となることが判る。容易に分かるようにカーネル（９）は下式になる：
νr+1(x) = νr(x) Σ 8 I(Ωi) g(Ωi) /Σ 8 g(Ωi)
i=1 Ii(Ωi) s2(xi) i=1 s2(xi)


次章で述べる実験では、初めの５回の逐次近似では g = I-0.2, 次の４回は g = I-0.8 が有効だった。

　３．アルゴリズムのテスト　

　テストに使った楕円体密度分布　

　(l, b) 面を 80 × 80 グリッドに分け、 輻射強度 I = ∫ds ν を 下の単純な楕円体密度分布 ν(x) を通して計算した。
ν(x) = (xe yeze)-1exp [ - ( rc2+x2 + y2 + z2 ) 1/2 ] 　(11)
xe2 ye2 ze2


ここに rc = 175 pc は計算の分解能にほぼ等しい。太陽 - 原点 (x = 0)線は (x, y) 面に対して角度 θ0 傾いている。また、太陽-原点線 の (x, y) 面への投影線は x-軸と角度 φ0 を成す。|x0 | = 8 kpc を仮定した。輻射強度の積分は s = 2 - 14 kpc で行った。 任意 (l, b) に対する I 値はグリッド点での値を２次元線形近似で得た。

　モデル密度　

　モデル密度は正の８分義区画 xmax = 4.2 kpc, ymax = 3.2 kpc, zmax = 2 kpc を被う、 25×25×10 直交座標 グリッド上で定義される。|x| ≤ xmax, |y| ≤ ymax, |z| ≤ zmax の直方体領域を "boundary box" と呼ぶ。 モデルの方向は一般には、真の分布とは異なる θ, φ を向いている。 ∫ ds ν の積分に使う ν は "boundary box" グリッド点での値を内挿して用いる。 "boundary box" を外れる視線方向に対しては十分小さい値を与えておく。 図１に見られるように "boundary box" の投影は天空上で不規則な形を示す。

　実験１　

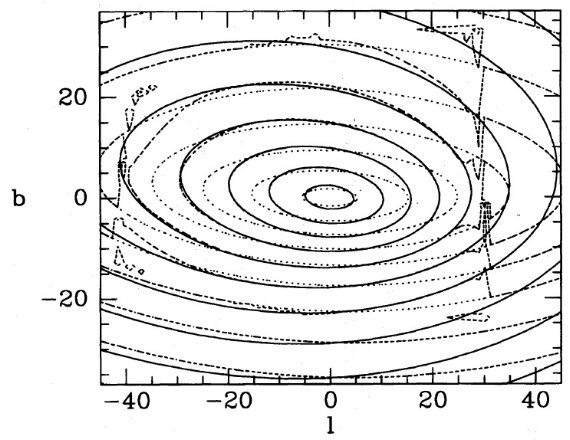
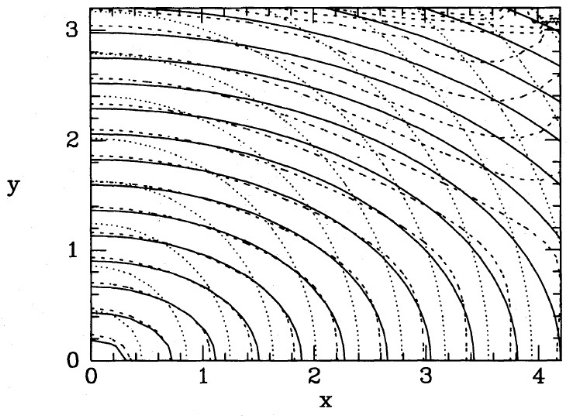
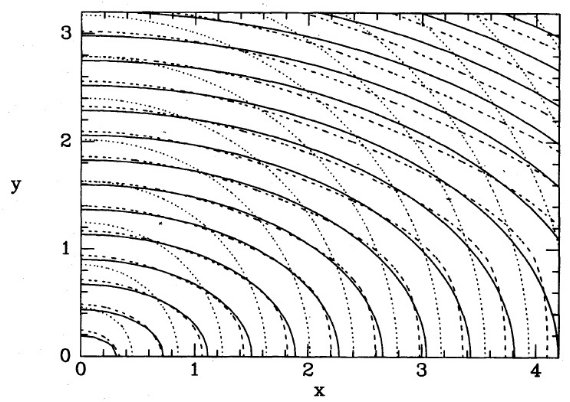
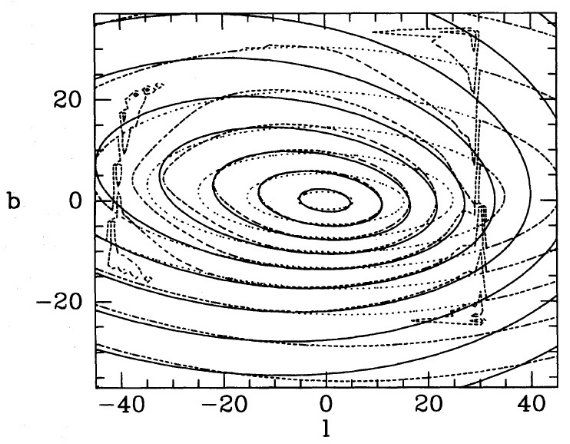
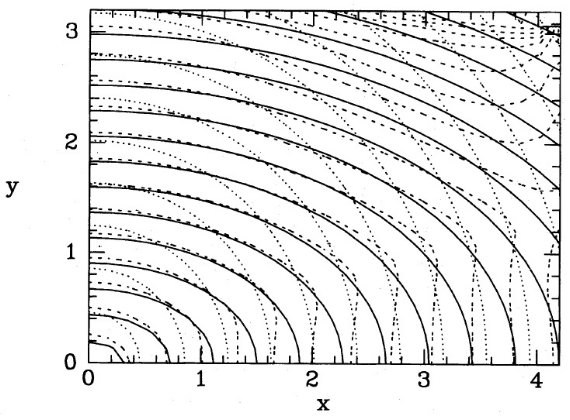
　図１は θ0 = θ = 7°, φ0 = φ = 18°, (xe, ye, ze) = (0.5, 0.3, 0.13) kpc でのテスト結果である。実線＝真の密度分布。点線=スタート分布。 破線＝９次近似解 I9。"boundary box" の縁に I9 の 等高線が集まってきている。その内側では R-L 法で修正が行われ、その外側では 最初の仮定のままである。この不連続転移は初期分布が不適切だった現れである。

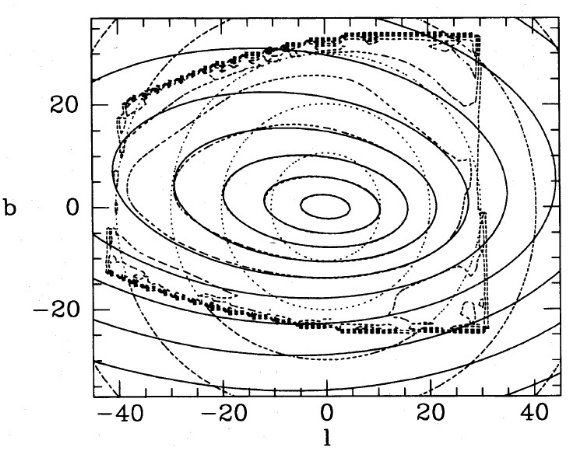
図１．θ0 = ．θ = 7°, φ0 = φ = 18° でのテスト。実線＝真の密度分布。点線=スタート分布。 破線＝９次近似解 I9。 I9 等高線は境界箱シルエットの縁に 集まる。なぜならその外側では I9 = I0 だから。


図２．図１と同じだが、スタート分布を扁平にした。ν0 を式１１ の (xe, ye, ze) = (0.4, 0.4, 0.15) kpc で与えた。境界の集中が弱くなっている。




図３．図２の密度分布。実線＝真の密度分布 ν の (x, y) 面上の等高線。 点線=スタート分布 ν0 。破線＝９次近似解 ν9。



　図２の解説　

　図１で起きた、境界での近似線の集中は初期推定が悪かった結果である。 図から真の分布がもっと扁平なことが判るので、次に扁平な初期値から出発した。 その結果が図２である。境界の強調はずっと弱くなった。実線と破線との乖離は 右上方部に限定されるている。ここは "boundary box" の効果が最も厳しい。

　図３の解説　

　図３には図２の逆変換として、 (x, y) 面上での等密度線を示す。破線が内側で 真の分布を良く追随していることが判る。使用したアルゴリズムはバー形バルジを 正しく導き出した。破線（近似解）は x ≤ 3 kpc までは真の解を再現しているが、 その先では上向きに反ってしまう。この効果は図２の右上でモデルの表面輝度 を上げる必要から生じた。特に、逐次近似が細長過ぎる初期値から出発した場合、 例えば、 (xe, ye, ze) = (0.6, 0.3, 0.15) kpc というような値、 "boundary box" による丸め作用が逆に働き、図３の破線は大きな x では破線を下に押し下げる働きをする。

図４．図３と同じだが、"boundary box" を (6, 4.6, 2.9) kpc へ広げた。




図５．θ0 = θ = 7°, φ0 = 30°, φ = 18° でのテスト結果。ミスマッチの特徴が分かる。



図４の説明　

　図４ではその点を強調するために、拡大した "boundary box" による計算の結果を示した。 "boundary box" による人工的な影響が除去されていることが判る。

　図５の説明　

　図５には分布の主軸方向が回転した場合の結果を示す。実際に使用した パラメタ―は、θ0 = θ = 7°, φ0 = 30°, φ = 18° であった。残差に独特なパターンが認められる。真の等高線とモデル 等高線が中心の周り一回転の間に三回も交差するのである。

　図１−５を見て　

　図１−５を見ると、θ0 = θ = 7° に対しては、 R-L 法で満足な再現に成功している。太陽 - 中心線が主平面に乗っていなけ れば同様に良い結果が得られるだろう。
(ということは、x-y 面が銀河面と一致 していたら、ありそうな事態だが、無理と言うことか？ )


図６．ln (I/Ir) の rms 残差。三角＝図１．四角＝図２，３． 五角形＝図５．六角形＝図７．



　図７の説明　

　図７は、太陽ー中心線が主平面上にあり、θ0 = θ = 0°, φ0 = φ = 18° である。この場合の R-L 法 は上手く働かない。モデル等高線は突然下に折れ曲がる。数値実験で φ を変えると折れ曲がり角度も変化する。

図７．図３と同じだが、太陽ー中心線が銀河面上にあり、 θ0 = θ = 0°, φ0 = φ = 18° である。破線（モデル）は x - 軸の周りに肩が出来ている。 その角度は φ に近い。
( 面対称になっていると、x 軸で折れ曲がらないか？ 角度 φ の折れ曲がりって何が原因か？ )



　なぜ変になるのか？　

　この場合、対称面の上下の像はもはや独立な情報を与えない。θ ≠ 0 ですら 投影の逆変換に一意性は保証されていないので、&thetal = 0 の場合にアルゴリズムが おかしな分布を拾ってしまうことは無理もない。回復密度と真の密度との差は x - 軸の周りの負密度の円錐状領域と、太陽ー中心線付近の正の稜線とからなる。 (Gerhard, Binney 1996)



図８．ノイズのあるデータ。左：図３と同じだが、 l = 20 の先では支配的になる ガウスノイズを加えた。分散は 0.001 I(0, 0) である。右：もっと浅い輝度分布 に対する逆変換の結果。

　４．結論　

　非軸対称分布の回復　

　Richardson - Lucy アルゴリズムを面対称を持つ分布に対して適用した。 最初に仮定した主軸方向が実際と大きく離れていても、アルゴリズムは正しい 方向を導き出した。適切な出発からはアルゴリズムは銀河面上の非軸対称性を 正しく検出できた。

　太陽ー中心線が主平面に近い場合　

　太陽ー中心線が主平面に近い場合、回復された等密度面は非現実的に角ばった 形となる。その場合でも全体の細長さは回復された。 		中心部の高 S/N 領域は保存される。

　データのノイズが大きいとアルゴリズムは上手く働かない。一般には S/N ≥ 1 なら意味ある結果が期待される。幸運なことに、データの質が高い中心付近での結果が 低質の周辺部データにより大きく影響されることはない。

　COBE/DIRBE データ　

　COBE/DIRBE データの誤差がこのアルゴリズムの適用を可能にするレベルかどうかが 大きな興味がある。