The Maser Strength of OH/IR Stars, Evolution of Mass Loss and the Creation of a Superwind

　アブストラクト　

　１．イントロダクション　

　２．OH 光度とマスロス率　

サヘルサイズとマスロス率　 　Elitzur et al 1976 モデルは L35 ∝ LOH を予想している。 L35 はマスロス率と相関するだろう。 Bowers, Johnston, Spencer (1981) はマスロス率とシェルサイズの関係を見出した。従って、シェルサイズと マスロス率の間に関係があるに違いない。 　表１　距離　 　表１にシェルサイズの分かっている OH/IR 星を載せた。第３列の距離は 次の３つのどれかで決めた。 （i）周期光度関係。ミラ型星。 Nguyen-Q-Rieu et al 1979. （ii）接点距離。Vlsr > +100 km/s. Rgc=10 kpc 仮定。OH25.1-0.3, OH30.1-0.7, OH18.5+1.4 の距離は Rgc に比例する。 （iii）位相遅れ距離。 ただし、IRC-20197 と VX Sgr の距離は L = 10,000 Lo を仮定して決めた。 VY CMa の距離は星団に付随すると考えた。 　表１　シェルサイズ　 　表１第４列にはシェルサイズを載せた。アステリスクが付いているのは位相遅れ から決めたサイズで、距離と無関係。その他は OH マップで求めた角サイズに 距離を掛けて決めた。 　マスロス　 　表１第６列のマスロス率は赤外観測に基づいている。

表１．シェルサイズ測定のある OH/IR 星

図１．LOH(Jy kpc2 と シェル半径。 白丸＝可視ミラ。黒丸＝ 不可視 OH/IR 星。 　図１＝ LOH と ROH の関係　 　図１で LOH と ROH の関係をプロットした。数値の エラーに拘わらず、両者の相関は明らかである。可視ミラと不可視 OH/IR 星 の間で LOH と ROH が重なっていることは、二つの 星グループが連続的に変遷していくことを示す。 　　　LOH ＝ 4 ROH2 (ROH in 1016 cm)　　　　　　　　　　　　(1) この勾配は赤外観測からのマスロスとも良く合う。 　マスロス式 　 　　　dM/dt = 4πρ(ROH)Ve ROH2　　　　　　　　　　　　　(2) OH メーザーに必要な OH 最低コラム密度は 1017cm-2 である。これは水素分子に直すと 　　　N(H2) = 6 1020cm-2 　　　 　　　　　　　　　　　　　　　　(3)　　 OH メーザーの表面輝度はほぼ一定らしいので、式（３）が全てのメーザー源に 適用可能と仮定する。密度変化を逆二乗則として、ROH から 外側へ積分すると、コラム密度は、 　　　N(H2) = nH2(ROH)×ROH である。

図２．LOH(Jy kpc2 と dM/dt (Mo/yr) の関係。 マスロス率は赤外観測から決めた。 　式（２）を dM/dt = 4πμ(H2)Ve nH2(ROH)× ROH 　　　= 4πμ(H2)N(H2)VeROH ROH = (dM/dt/Ve)/[4πμ(H2)N(H2)] を（１）に代入すると、 　　　LOH = 3 1013[(dM/dt)/Ve]2 Jy kpc2　 　　　　　　　　(4) ここで、 dM/dt は Mo/yr, Ve は km/s 単位である。 　式 (4) のチェック　 　式４は独立に求めた dM/dt でチェックされる。赤外観測からは、可視 OH/IR 星で 5 10-6 Mo/yr (Hyland 1980)、不可視 OH/IR 星で 3 10-5 Mo/yr (Werner et al 1980) という典型値が得られた。 Ve = 15 km/s で 式 (4) を使うと可視ミラで 4 Jykpc2, 不可視 OH/IR 星で 130 Jykpc2 となる。これは観測される LOH と合う。この結論は図２で、赤外から決めた dM/dt を 電波からの LOH を較べて、支持される。つまり、式４は低光度 の近傍 OH 放射ミラから非常に明るい不可視 OH/IR 星への遷移が質量放出率 の遷移に伴うことを示す。 　以前の研究　 　Nguyen-Q-Rieu et al 1979 は LOH と [3.5-10] カラーの 相関図を示した。 Jones et al 1982b は LOH/L* = Mbol - MOH と (L-M) との相関を示した。現在進行中のプログラム では、LOH/LIR と [4.8-12.5] の相関が明らかに された。しかし、これまでに LOH と dM/dt との間の関係を 明示した例はない。

　３．OH 光度関数とマスロスの進化　

図３．OH 光度とマスロス率の時間変化。式５と式６．OH メーザー寿命 tOH = は主系列質量 0.7 - 6 Mo に対して、0.6 - 6 105 yr となる.(表２参照) 時間の大部分は低マスロス率期間である。メーザー寿命 の最後の 1 % 期 = 600 - 6000 年間が OH/IR 星として銀河のどこからでも 見られるほど明るくなる。 (この "明るい" は OH メーザー光度の 意味と思うが、明確でない。L* だったら大変。 ) マスロス率の変化は改訂レイマース則で表す。 　dM/dt の時間進化　 　前章で LOH が主に (dM/dt) で決まることを見出した。観測から、 LOH ∝ (dM/dt)2 となることが分かっている。 LOH の分布巾が広く、第１近似では Mms に依存しないことから、 我々は、与えられた Mms に対し、様々な LOH = 様々な (dM/dt) の OH/IR 星があると結論する。つまり、一つの AGB 星の LOH と (dM/dt) は時間と共に増加していく。 (時間変化への結論は論理では出てこない ように思える。 ) 　LOH 光度関数　 　 Baud, Habing, Matthews, Winnberg (1981) では、LOH の光度関数 ψ(LOH)dLOH = dLOH 巾内の OH/IR 星数として定義した。そこでは ψ ∝ LOH-α とした時、α = 1.65 とした。最近 Olnon (p.c.) は３つのサーベイを再解析して、α = 2 ±0.1 を 得た。 我々もこの値を採用する。 　進化の方程式　 　LOH の光度関数は、光度進化のスピードを反映すると考え、 (どの Mms 星でも同じ進化を辿ると考えて いるから。) 　　　 ψ(LOH)dLOH = βLOH -αdLOH = (NOH/tOH)dt (本文では NOH でなく LOH と書いてあり混乱する。) ここに tOH = AGB 離脱の時間、 β = 規格化定数、α = 2、 Lmin = t=0 の時の OH 光度、Lmax = tOH の時の最高 OH 光度。表１を 見ると、妥当な値は Lmin = 1 Jy kpc2, Lmax = 1000 Jy kpc2 あたりである。上式を積分すると、 　　　β/(1-α)[Lmax1-α-Lmin1-α] = NOH 　　　β = NOH(1-α)/[Lmax1-α-Lmin1-α] 方程式の解は、 　　　β/(1-α)[LOH(t)1-α- Lmin1-α] = NOHt/tOH 　　　LOH(t) = [NOH(1-α)t/(tOHβ) + Lmin1-α]1/(1-α) 　　　　　　 = Lmin[1+[Lmax1-α-Lmin 1-α]t/tOH/Lmin1-α]1/(1-α) 　　　　　　 = Lmin[1+(Lmax1-α-Lmin1-α)t/tOH /Lmin1-α]1/(1-α) 　　　　　　 = Lmin[1+[(Lmax/Lmin)1-α-1]t/tOH]1/(1-α) 　　　　　　 = Lmin[1-A(t/tOH)]1/(1-α) 　　　　　　　　　　　　　　(5) ここに、A = 1-(Lmax/Lmin)1-α である。式 (4), (5) を使 い、 Ve = 一定と仮定すると、 　　　dM/dt = (dM/dt)min [1 - B(t/tOH)]1/2(1-α)　　　　　　　(6) ここに、 B = 1 - [(dM/dt)max/(dM/dt)min]2(1-α). 観測 される範囲では A = 1, B = 1 としてよい。厳密に言うと、これは、 t → tOH の時、 L OH → ∞, dM/dt → ∞ を意味する。しかし、それは脈動の最終時期のみの問題である。また、Lmin, Lmax, (dM/dt)min, (dM/dt)max, tOH は Mms の関数であろう。

表２．OH/IR 星のパラメタ―。第３列＝メーザー開始時(t=0) のマスロス率。 第４列＝開始時コアマス。第５列＝熱パルス開始時のコアマス(Iben 1981). 第６列＝ WD マス。第７列＝開始時星光度。第８列＝開始時外層マス。 第９列＝メーザー寿命。 (低質量ほど短いのはちょっと変。 ) 第１０列＝ Baud, Habing, Matthews, Winnberg (1981) のメーザーサーベイ(感度 Ls = 100 Jy kpc2)による相対空間密度。 最終期での OH 消灯の効果は入っていない。 第１１列＝ OH 最高光度 Lmax。第１２列＝　Ls < LOH < Lmax にあって、 BHMW サーベイに掛かる状態の星の相対空間密度。 ( ) 　マスロス進化最終期＝超星風　 　図３には、式 (5), (6) をグラフで示す。α = 2, Lmin = 1 Jy kpc2, Lmax = 1000 Jy kpc2 を仮定した。大部分の時間 LOH は低く、 Lmin 付近にあることが分かる。この 低光度期は太陽近傍に見られる可視ミラである。AGB 進化の最終時期にのみ OH/IR 星が現れ、銀河のどこからでも検出可能となる。OH 光度関数から導いた OH/IR 期への遷移は連続的となる。しかし、 Baud, Habing, Matthews, Winnberg (1981) が用いたデータはダブルピーク型の光度関数を否定するには不十分であった。したがって、 非連続な遷移もあり得る。 　超星風期の長さ　 　　　Lc = Lmin/[1-(tc/tOH)] = Lmin[tOH/ (tOH-(tc) 　　　(tOH-(tc) = tOH(Lmin/Lc) Lmin = 1 Jy kpc2, Lc = 100 Jy kpc2 とすると、 OH メーザー放射期の 1 % が星風期であることになる。 (これは勿論光度関数の数比からも容易に出る。 ) 　超星風期の太陽近傍での評価　 　観測的には、太陽から 1 kpc 以内にある、弱いまたは明るいタイプ II OH 源 = 可視ミラ、M-超巨星、 IRC 天体、は大体 45 あるが、超巨星 NML Cyg を除いては 100 Jy kpc2 である。OH サーベイはフラックスリミッテッドである から、弱い電波源はサーベイから漏れる。無バイアス銀河面サーベイは太陽近傍の 明るい OH 源としてあと一つ OH 25.5+0.6 を見出した。これで、 4 % にあるが、 上で評価した 1 % とは矛盾しない値と言える。 　放出量＝外層質量　 　tOH の間の放出量＝外層質量 Me と考え、式６を積分し、 　　　dM/dt = (dM/dt)min[1-(t/tOH)]-1/2 　　　Me = 2tOH(dM/dt)min 　　　tOH = Me/[2(dM/dt)min]　　　　　　　　　　　　　(7)

　この節のまとめ　

　４．星のパタメタ―を用いるマスロス進化　

　５．Mms と Ve の関係　

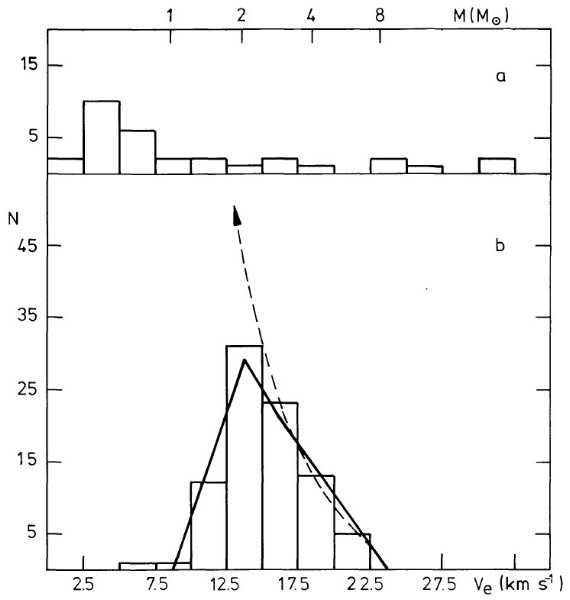
Ve と星年齢（主系列質量）の関係　 　 Baud, Habing, Matthews, Winnberg (1981) は Ve と星年齢の間に相関を見出した。図４a には Nguyen-Q-Rieu et al 1979, Engels 1979, Olnon et al 1979, Wilson, Barrett (1972) から採った、 < 1 kpc の近傍ミラの Ve 分布を示す。図４b は遠方、非 可視の OH 光度が高い OH/IR 星の Ve 分布。それらは銀河全面に及ぶ電波サーベイと Baud, Habing, Matthews, Winnberg (1981) = BHMW の l = 10 - 50 サーベイから採った。それらの大部分は太陽から 7 - 10 kpc 離れた分子リングに属している。二つの分布の違いは驚くほど大きい。OH 放射 の可視ミラ型星は Ve = 3 - 30 km/s と非常に Ve 分布巾が大きい。弱いピー クが低 Ve 側にある。一方、非可視 OH/IR 星は目立つピークが Ve = 15 km/s で、分布巾は狭い。また Ve < 15 km/s の例はない。そこは可視ミラ型星 の大部分がある区間である。可視ミラの方のサンプルは一様ではないが、可視 ミラと非可視 OH/IR 星との速度分布に関する差は選択効果でなく、事実であ ろう。これが意味するところは、Ve <: 10 km/s, つまり Mms < 2 Mo (BHMW), の星で非常に明るい LOH にまで届くものはほんの僅かし かいないということである。BHMW では第１近似で ψ(LOH) は Ve に依らないとしたが、この事実はそれに反する。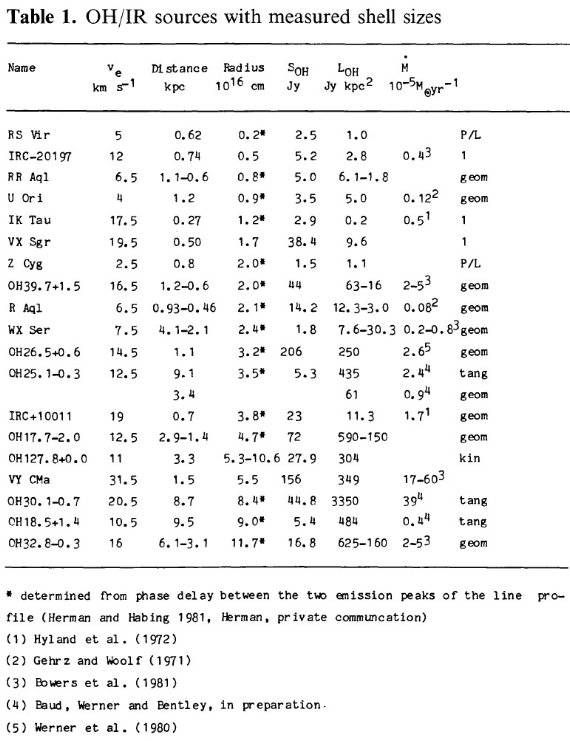 　LOH > Ls である OH/IR 星の 質量分布関数　 　 Bowers et al. (1978) や Baud, Habing, Matthews, Winnberg (1981) は OH/IR 星の大部分が R = 5 kpc 分子リング上に位置し、太陽から大体等 距離であることを見出した。そこで、我々は図４b サンプルには BHMW 観測感 度に対応する LOH 光度 Ls 以上の OH/IR 星が全て含まれている と仮定する。 (実質的に体積・光度リミッテドに なっているという意味。 ) 　Ve と M は相関するので、N(Ve)dVe = N(M,Ls)dM とする。N(M,Ls) は LOH > Ls である OH/IR 星の質量分布関数。φ(M) = 現在 の質量関数、t*(M) = 主系列寿命、NOH = OH/IR 星密度、ψ (LOH) = OH 光度関数、として、 N(M,Ls)dM = ψ(M) tOH [∫ ∞ φ(LOH) dLOH ] dM t*(M) Ls NOH ( この式は、ψ(M)dM が dM 区間内の星数(実質的には主系列星数)、それに tOH/t*(M) を掛けて dM 内の HO 放射星の数、さらに [∫...dL]で、dM 内で、OH 強度が Ls 以上の OH/IR 星の数となっている。 この式を見ると、M に依存する項 ψ(M)/t*(M) は進化フローレイト。この 項以外は M 依存性はない。つまり、Ls 以上での M 分布は進化フローレート に比例している。OH 期の進化が共通と仮定しているので当然と言えば当然。) BHMW に倣い、ψ(LOH) は Ve つまり Mms に依存しない。 ψ(LOH)/t*(M) は初期質量関数 ξ(M) ∝ M-2.5 (Miller, Scalo 1979) に等しい。ψ(LOH) ∝ LOH-2 で積分して、 　　　N(M,Ls) = C M-2.5 tOH(M) Λ(Ls)　　　　　　 　　　　　(12) ここに、Λ(Ls) = (Lmax-1-Ls-1)/ (Lmax-1-Lmin-1) Ve > 15 km/s で、Ve 増加と共に OH/IR 星の数が急減するのは単に、初期 質量関数の勾配の反映に過ぎないことが判る。

図４．a: タイプ II OH （1612 MHz 最強）の近傍可視ミラと超巨星の Ve 分布。 b: BHMW による L = 10 - 50 にある非可視 OH/IR 星の Ve 分布。 破線＝ LOH に下限を設けない場合のモデル分布。実線＝ Lmax(Ve) を設けた場合のモデル分布。 (星質量の出典は？ ) 　Ve と M の関係　 　Ve = [3, 10] km/s は P = [300, 500] d ミラで、 Mms < 1 Mo である。 Ve = [10, 15] km/s 星の運動は M = 2 - 3 Mo に合うことを BHMW は見出した。 Ve > 15 km/s は M = [3, 10] Mo であろう。そこで、 　　　Ve = γ log(M/Mo) + δ 　km/s　　　　　　　　　　　　　(13) と仮定し、観測値にフィットして、γ, δ を決めることにした。 それには、式１２を図４b に逐次的にフィットしていく。その際には Lmax = 1000 Jy kpc2, Lmin = 1 Jy kpc2, Ls = 100 Jy kpc2, Ls = 100 Jy kpc2 とした。その結果、 γ = 16, δ = 8 km/s を得た。

　Appendix： 表２の星パラメタ―を決める逐次近似の方法　

　 γ, δ の決定について　

　６．議論　

　今後