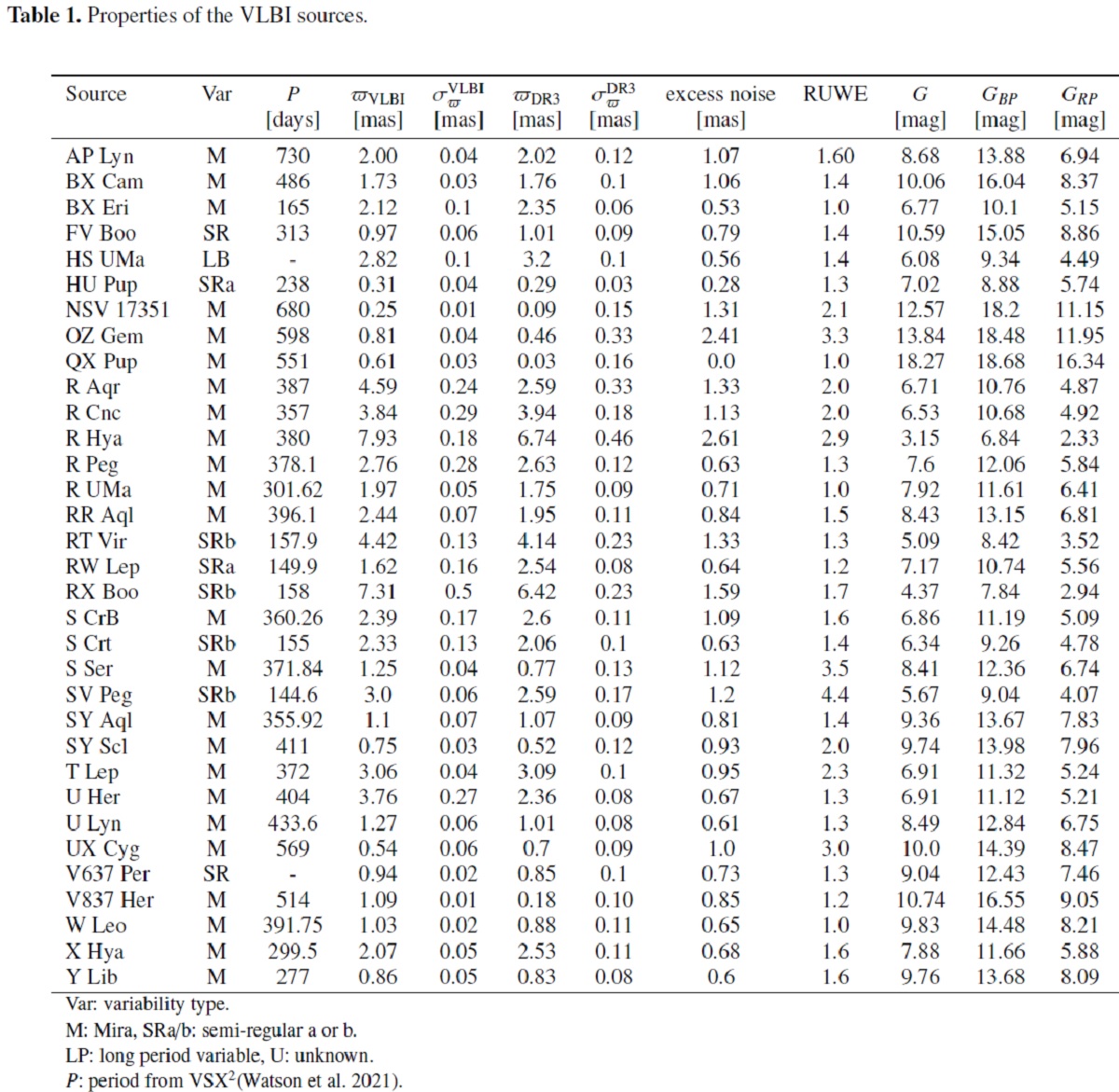
| Gaia DR3 視差をO-リッチの 33 AGB 星 VLBI メーザー視差と比べ、DR3 視 差に対する統計的補正ファクターを得た。次に、補正された Gaia 視差と 以前に得られた AGB 星の銀河分布からの事前確率 (prior) に対してベイズ法 を適用して、DEATHSTAR 計画からの 200 AGB 星距離を計算した。VLBI 星の SED を DUSTY モデルでフィットして、星の光度を求めた。 G < 8 mag の最も明るい星では、Gaia DR3 視差はファクター 5.44 低く 見積もられている事が判った。それより暗い 8 ≤ G < 12 ではファクター 2.74 である。Gaia DR3 視差ゼロ点オフセットは、明るい AGB 星で -0.077 mag である。より暗い AGB 星ではこのオフセット値はよりマイナス方向に振れる。 |
DR3 視差を補正すると、得られた距離は、我々のサンプルで、40 % 以上もの
非対称なエラーを伴うことが判った。銀河系 O-リッチミラ
型変光星の新しい周期光度関係は、 Mbol = (-3.31±0.24)[logP-2.5] + (-4.317±0.060) DEATHSTAR 星の新しい距離カタログを与えた。 DR3 視差の誤差が 20 % 以上の場合 AGB 事前確率に基づいて距離を求める際に は、距離がモデルに依存し、天体によりオフセットが変わるので、注意が必要 である。RUWE(re-normalised unit weight error) が 1.4 以下の場合、信頼で きる距離の保証はない。個々の AGB 星に対しては、距離の精度に RUWE のみを 使うことには問題がある。 |
1.イントロダクションAGB星の視差AGB 星の視差測定には次の困難が伴う。 (1)星周減光で暗くなる。 (2)星の半径が大きく、視差と角半径が同程度となる。 (3)対流セルが光球中心位置をずらす。 (4)明るい星では画像に飽和効果が生じる。 VLBI DEATHSTAR サンプル内の 200 近傍 AGBs を用いて GAIA DR3 視差の精度を 調べる。その為、 (1) Gaia と VLBI の視差測定データから視差補正ファクターを決定。 (2) ベイズ法で DEATHSTAR サンプル星の距離を決める。 (3) DEATHSTAR サンプル星の距離を PLR で決める。 (4) DEATHSTAR AGBs の距離カタログを作る。 |
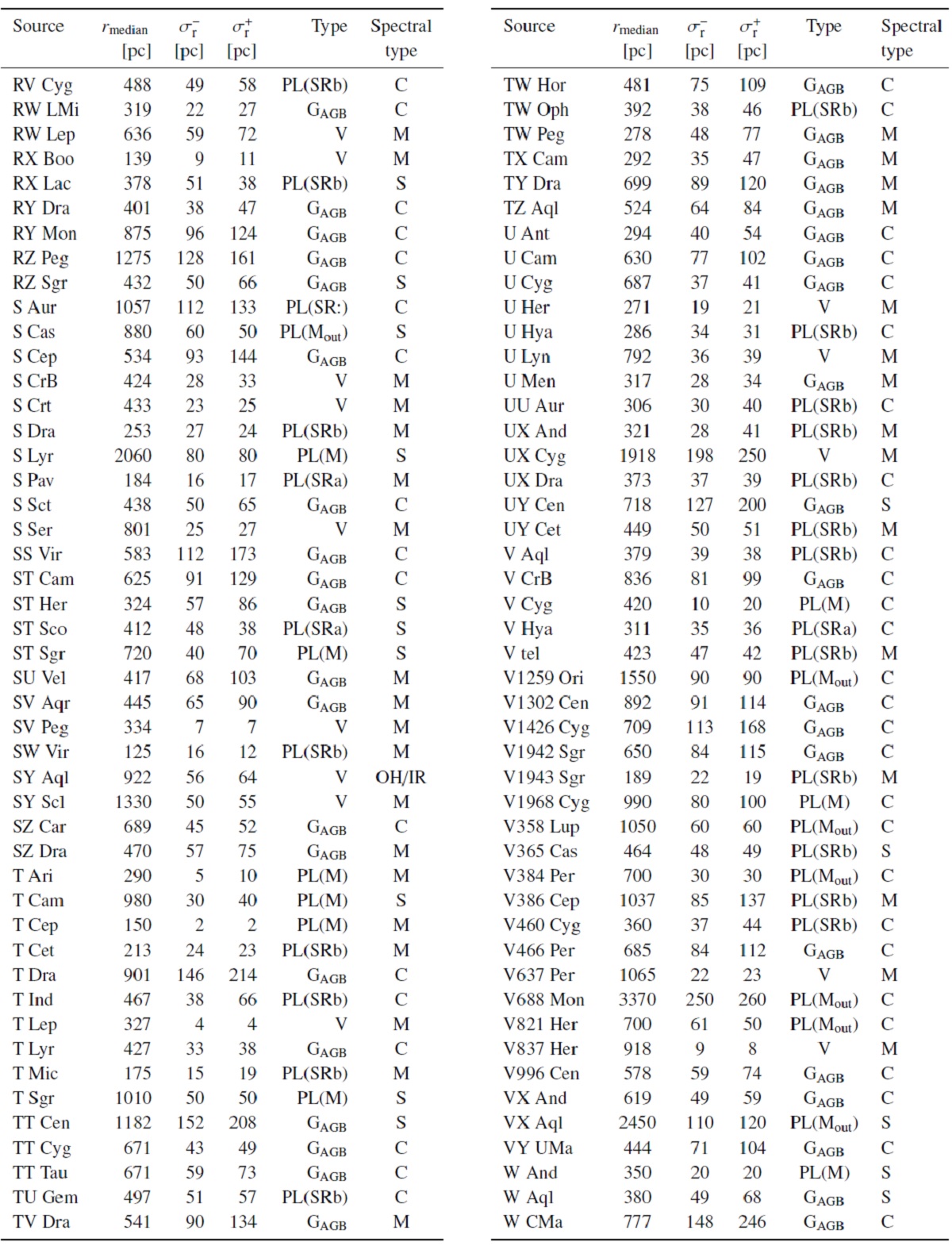
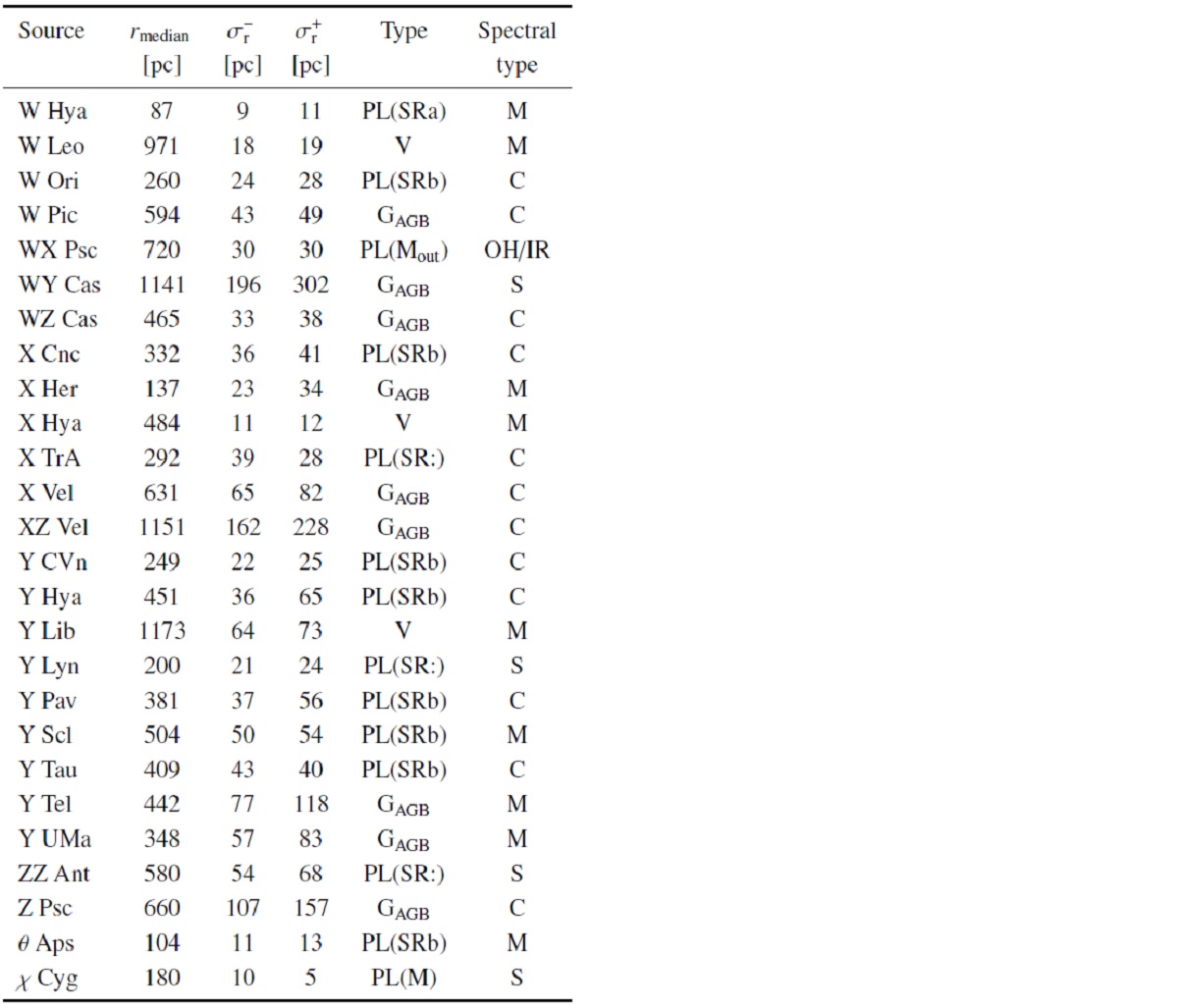
2.サンプルDEATHSTAR サンプル星は約 200 の AGB 星である。C-星は K < 2 mag で Schoier, Olofsson 2001 から採られた。非ミラ M-星は GCVS (Samus et al 2017)から、QI(12,25,60) = 333, F(60) > 3 Jy の基準で、 ミラ型 M-星は Gonzales Delgano et al 2003 から取られた。 S-星は Stephens 1984 と Jorissen, Knapp 1998 から採られた。 DEATHSTAR サンプルの 93 % は DR3 視差を持つ。 |

3.1.VLBI 観測3.2.VLBIサンプルVERA カタログ 2020 中の 29/99 天体は AGB とされている。 内、 3/29 = PPNe または post-AGBs, 26/29 = AGBs である。 Xu et al 2019 にも VERA 観測結果があり、AGB 星とされるが VERA カタログ と重ならない 13 星は、 6/13 = 超巨星またはハイパー巨星であった。 これらから BW Cam, R Cas, W Hya は VLBI 視差/誤差 < 5 なので落とす。 この結果、VLBI サンプルは 29 + 13 - 6 -3 = 33 である。 |
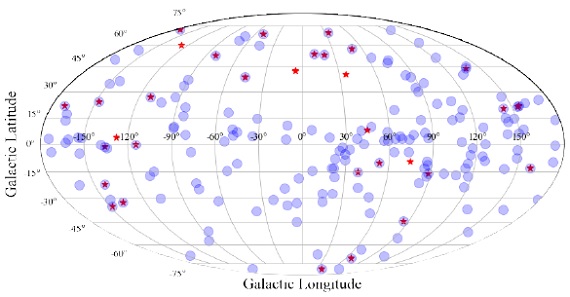 図1.サンプル星の位置。青丸=DEATHSTAR 星。赤星= VLBI 星。 |
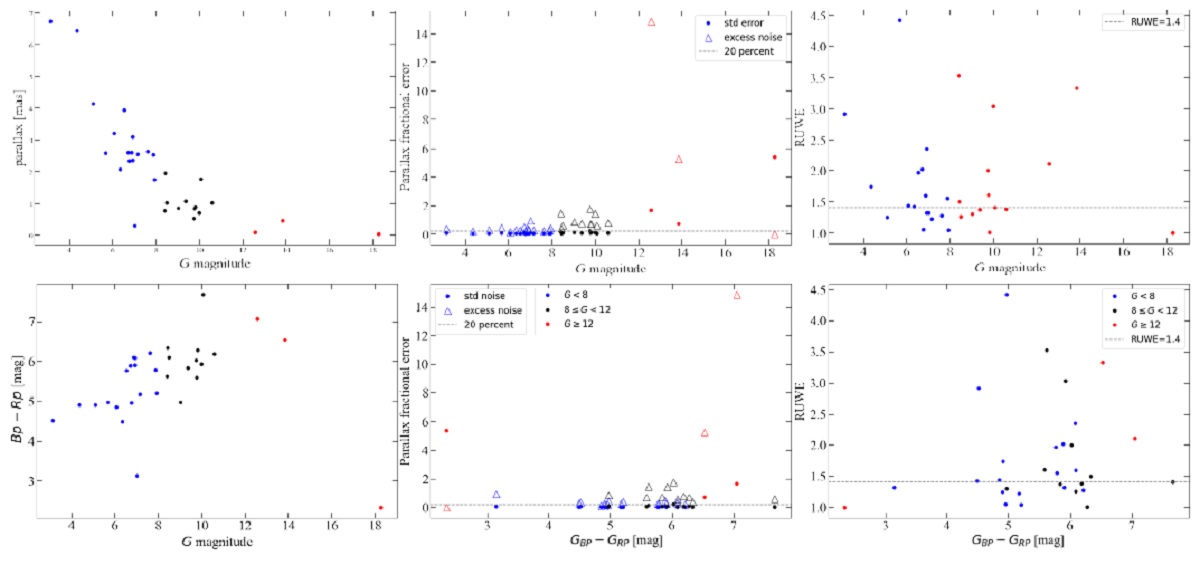
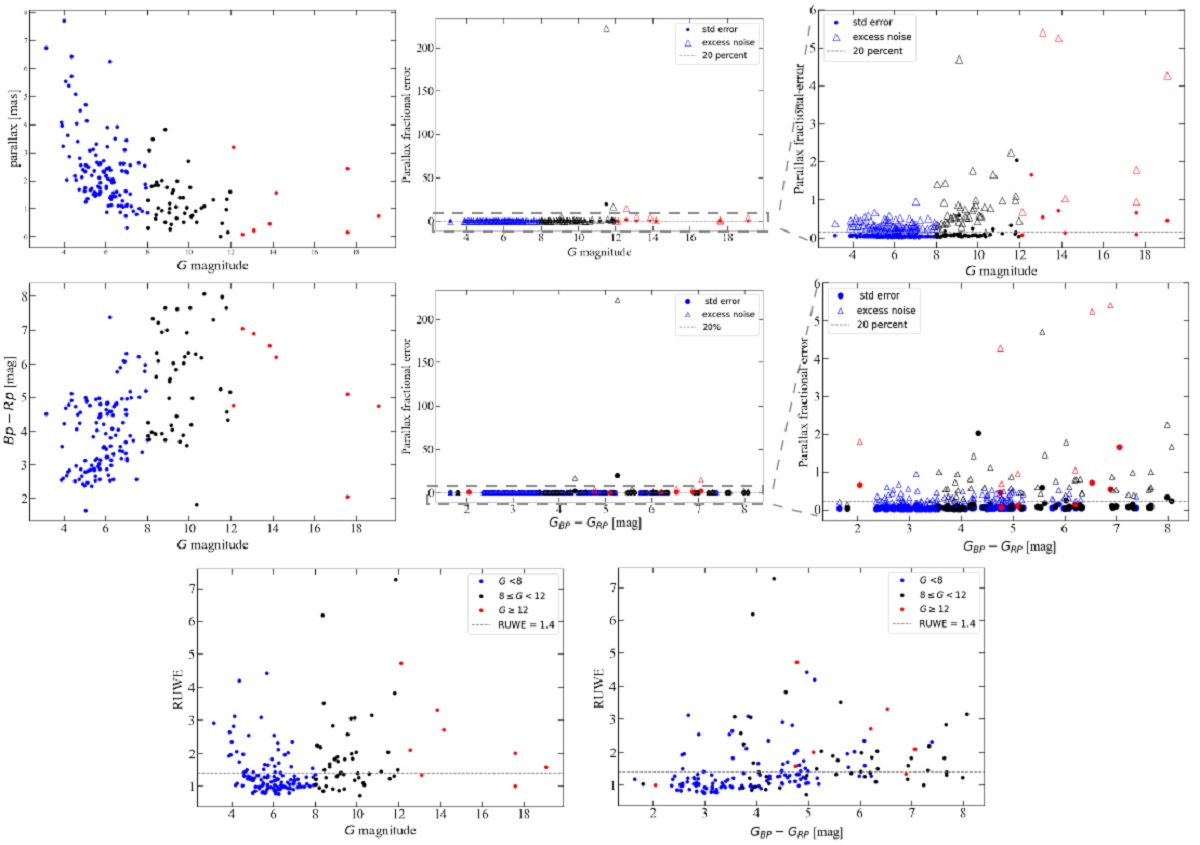
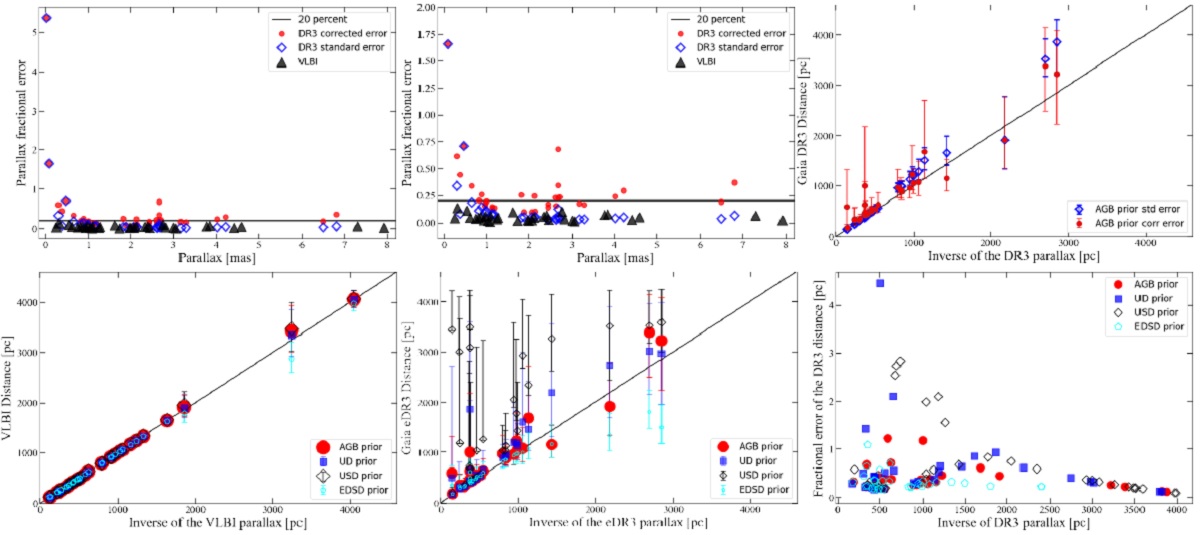
3.3.Gaia DR3 視差3.3.1.G 等級とカラー視差の相対誤差図2,3から G < 8 mag の星では 視差の相対誤差が 20 % 以下だが、 G = 8 - 12 でやや上昇することがわかる。 (この結論も適用範囲が不明。G 絶対等級が一定値なら良いが、視差の大きさ自体も関係するはず。) VLBI の暗い方3天体では、図2に示すように相対誤差が 75 % を越える。 (図2中央上段の赤丸3つの中央を 指して、 75 % 以上という言い方をしているらしい。トリッキー。) 図3の DEATHSTAR サンプルではその散らばりは一層大きい。 |
距離エクセスノイズ 距離エクセスノイズは G 等級が暗くなるにつれ大きくなり、 G = 8 mag の 先では明瞭に悪化して行く。 G 等級区分 G < 8, 8 < G < 12, G > 12 の 3 区分に分ける。 |
3.3.2.ゼロ点オフセットと誤差インフレーションファクター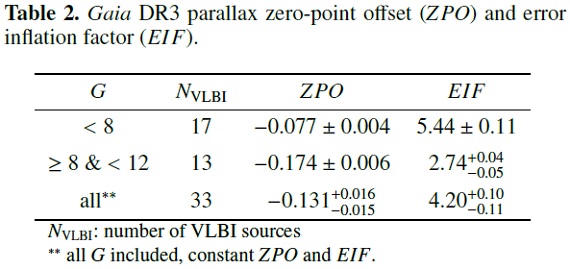 表2.Gaia DR3 ゼロ点オフセット (ZPO) と誤差インフレーションファクター。 視差の比較 図4には VLBI 視差 ωVLBIと DR3 視差ωDR3 を比較した。視差が 4 mas 以下では一致が良い。視差が大きい天体では散らばり が大きくなる。DR3 名目誤差 σωDR3 はVLBI 誤差 σωVLBI より小さい。しかし Gaia 誤差は過小評価されていることが判っている。カラー、表面輝度分布などの効果 で PMSs, Miras, binary pulsars には余分の誤差が加わる。 Gaia エラーの補正ナシ van Langevelde et al 2018 は DR2 と VLBI の視差を比較して、Δω= =ωDR3-ωVLBI の散らばりを説明するには、 追加のエラー astrometric excess noise を加える必要があるとした。 エラー補正なしでは、視差の差の分散は σω,tot = sqrt[ (σωDR3)2 + (σωVLBI)2] |
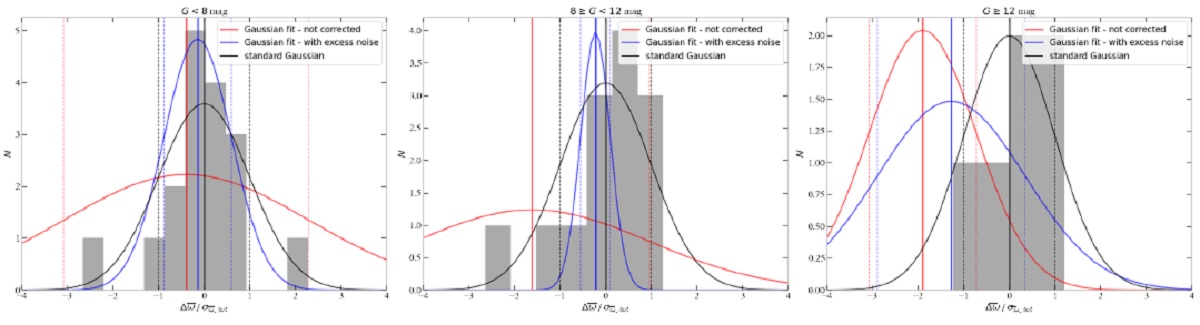
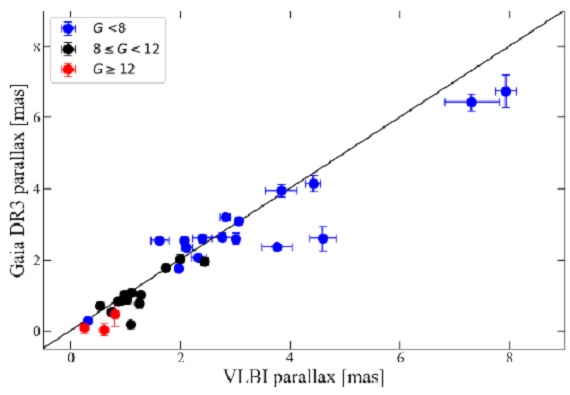 図4.VLBI と Gaia 視差の比較。 astrometric excess noise だが、astrometric excess noise が加わると、 σω,tot = sqrt[ (σωDR3)2 + (σωexcess)2 + (σωVLBI)2] となる。 EIF = error inflation factor この論文では、Gaia エラーを名目値より EIF 倍に大きくする。すると、 σω,totcor = sqrt[ (EIFσωDR3)2 + (σωVLBI)2] となる。図5に示す視差の差は total error で規格化されている。 (3種類の "total error" のどれを指すのか? それとも、観測的なΔω==ωDR3-ωVLBI の散らばりか?ただし差の平均をゼロにしてからだが。 ) 観測的総エラーで規格化してあるとする。 |
|
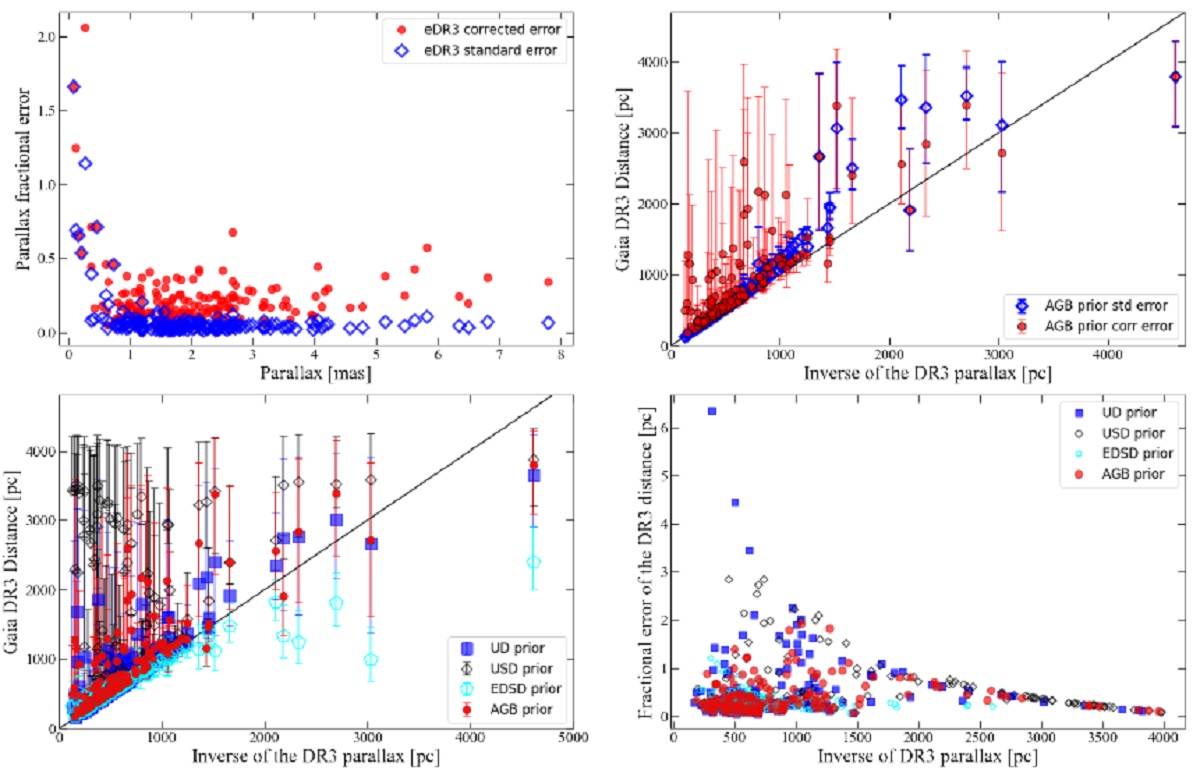
astrometric excess noise の比較 図6は、VLBIs に対しては DR3 の astrometric excess noise が DR2 の excess noise より大きいことを示す。DEATHSTARs に対しても 60 % の星で DR3 の excess noise の方が大きい。 補正ファクター 我々の結果は、 G < 8 mag の星に対する視差の誤差がファクター5以上 も過小評価されていることを示す。 G = 8 - 12 mag では名目エラーが大きく なるために補正ファクターは小さくなる。 G > 12 ではこの傾向は一層 強まり、補正ファクターは小さい。EIF 一定の適用は不適当である。 ゼロ点オフセット 表2に我々の得たゼロ点オフセットを示す。この値は、絶対値で Ren21 の -0.028 や Groenewegen21 の -0.039 より大きい。 |
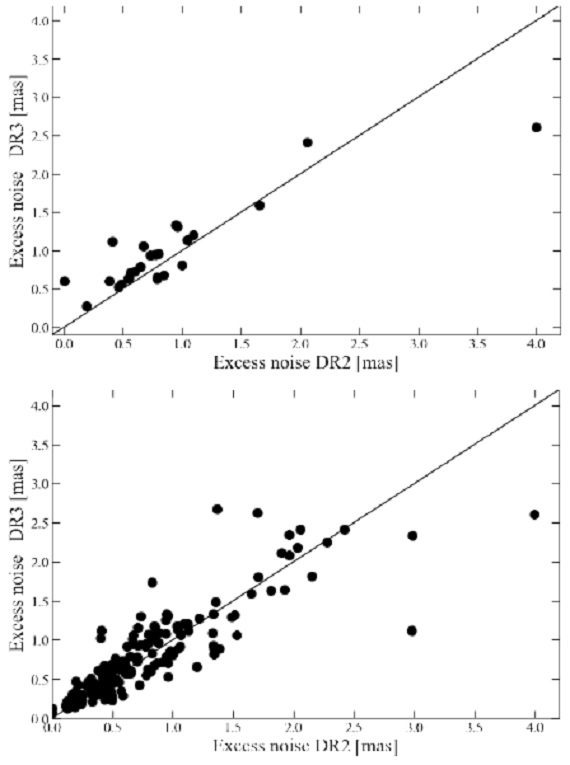 図6.DR2 と DR3 の astrometric excess noise 比較。 上=VLBIs。下=DEATHSTARs |
|
ベイズの定理 観測視差 ω が真の視差 ωTrue = 1/r の周りに 標準偏差 σω での正規分布から取り出された値と 仮定する。その時、観測視差の尤度は 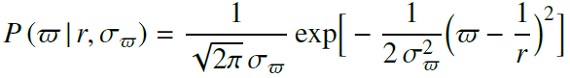 である。Bailer-Jones15 は視差の確率分布から距離を導く際の問題を指摘した。 より良い方法は、制度の低い視差観測から最も確からしい距離を推定すること である。そのような距離の事後確率分布は、 P(ω|r,σω)=(r,σω) の時に ω である尤度 と prior P(r)= 距離が r でありそうな事前情報 との掛け算となる。ベイズの定理は 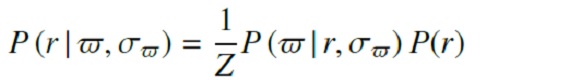 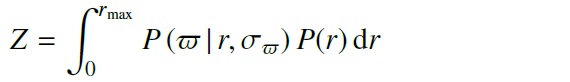 と表される。ここに、 P(r|ω,σω)=(ω,σω) の時に, r である確率 で、Z は ∫P(r|ω,σω)dr=1 とするための 規格化定数である。 Bailer-Jones 距離 Bailer-Jones21 は最も確からしい距離は事後確率分布の中間値であると述 べた。その結果得られる誤差分布は、1/ω から r への変換が非線形であ ることを反映して、非対称となる。Bailer-Jones15 によると、視差の相対誤差 が 20 % 以上だと、事後距離の分布は非常に非対称となる。 eDR3 天体では 視差の相対誤差が 20 % を越える。 距離の事後分布 VLBI, DEATHSTAR サンプル星に対して、距離の事後分布を計算した。 その際に重要なのは prior =事前確率の選択である。事前確率に多くの情報を 入れるほど、結果得られる距離のモデル依存度が高くなる。従って、事前確率 は予想されるデータを良く表現するように選ぶ必要がある。その為、4種類の 事前確率を試した。それらは、 (1) UD = r に関して一様な分布。Bailer-Jones15 の表記では、 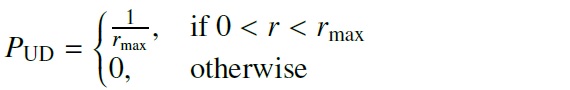
(2) USD = 空間に関して一様な分布。Bailer-Jones15 の表記では、 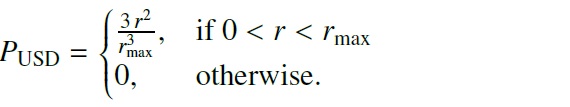
(3) EDSD = 指数関数減衰型分布。Bailer-Jones15 の表記では L = 250 pc、 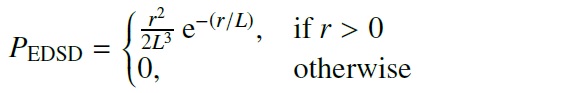
(4) AGB =より現実的な 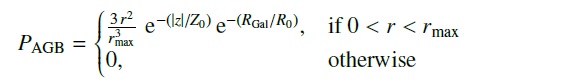
である。ここでは、 Jura, Kleinmann (1990), Jura, Kleinmann (1992) に従い、AGB 星の分布をスケール高 Zo = 240 pc, スケール長 Ro = 3.5 kpc の指数関数型円盤分布と仮定する。RGal = 銀河中心からの距離、 z = 円盤面からの光度である。 |
捜索範囲 sサンプル星の 2MASS K 等級分布は Ks = 3.2 mag が限界等級になっている と判った。太陽質量星の AGB 先端等級を M(V) = -2 mag, (V-K)o = 8 と Bladh, Hofner, Nowotny, Aringer, Eriksson (2013) 理論モデルから見積もると、M(K) = -10 mag から、最大距離は DM = 3.2+10 =13.2. logD(pc) = 13.2*0.2 +1 = 3.64. D = 4.4 kpc となる。そこで、我々 のサンプルの許容最大距離 = 4.5 kpc とする。 採用事前確率 今回採用した AGB 星事前確率は Jura, Kleinmann (1992) の分布関数である。それは Ishihara et al. (2011) が見出した、 O-リッチ星が銀河系動径距離と共に減少し、C-リッチ星は太陽から 8 kpc 以内で一様な分布、という結果と一致する。 Jackson, Ivezic, Knapp (2002) は 5 kpc 以内で一様な分布で、スケール高 300 pc であり、かつ その上では スケール高 1.6 kpc で 銀河面上 12 kpc まで広がっていることを見出した。 我々が採用するスケール長はこの二つの研究と一致する。スケール高 Zo や スケール長 Ro を変えても結果にあまり影響しない。導かれる最終距離に 最も大きく影響するのは許容最大距離 rmax である。この値を下げ ると、事後確率が収束しなくなって、距離の値が上限値に張り付くケースが増え る。rmax を 5 kpc に上げると、DEATHSTAR サンプルの二星のみの 距離が変わり、新しい限界値(5kpc?)に移した。つまり、これらの距離は 怪しい。 視差相対誤差 視差相対誤差が 18 % より大きい場合、いくつかの星で導かれる距離のエラ ーが 20 % を越えることが判った。誤差のカットを 20 % にすると、一層大き な不定性が生じる。 VLBI サンプルの 85 % は DR3 視差相対誤差 0.2 以下で あった。しかし、第3章で議論した Gaia DR3 視差への補正を行うとこの 数字は 35 % に下がる。 (意味不明) DEATHSTAR 星の場合、補正前には 94 % が視差相対誤差 0.2 以下であるが、 補正後は 52 % に下がる。(表A.1.を見よ) VLBI 距離 VLBI 視差を使って、4つの事前確率から導かれた距離は殆ど変化しない。 その様子を図7に示す。VLBI 視差の相対誤差は 30 % 以下で、そのような場 合、事後確率はデータの尤度により支配されるので事前確率の選択は結果に 響かないのである。導かれた距離の相対誤差は 20 % 以下で、信頼度の高さを 表している。 事前確率の影響 補正 DR3 視差から導かれた距離は事前確率の影響を大きく受ける。視差相 対誤差が大きい場合には事前確率が事後確率を支配するからである。図7と 図8の様々な事前確率で得られる距離の比較は、導かれた距離に対する視差 相対誤差の影響を示す。ここから先では (iv) の AGB 事前確率に集中する。 これが最も現実的だからである。不定性が大きくなると、真の視差は測定視差 よりも小さい確率が大きくなる。その結果、我々が得る真の距離は大きくなる。 これは Lutz-Kelker バイアスとして知られている。測定の相対誤差と事前確 率の感度とが効果の大きさを定める。 距離相対誤差 Gaia DR3 補正視差と AGB 事前確率を用いて、DEATHSTAR サンプルの 46 % は距離相対誤差が 25 % 以上と分かった。15 % 以上は距離相対誤差 50 % 以上である。事前 及び/または 事後確率分布が収束しなかった時には、又は 相対誤差があまりに大きかった時にはその距離を棄却した。 |
|
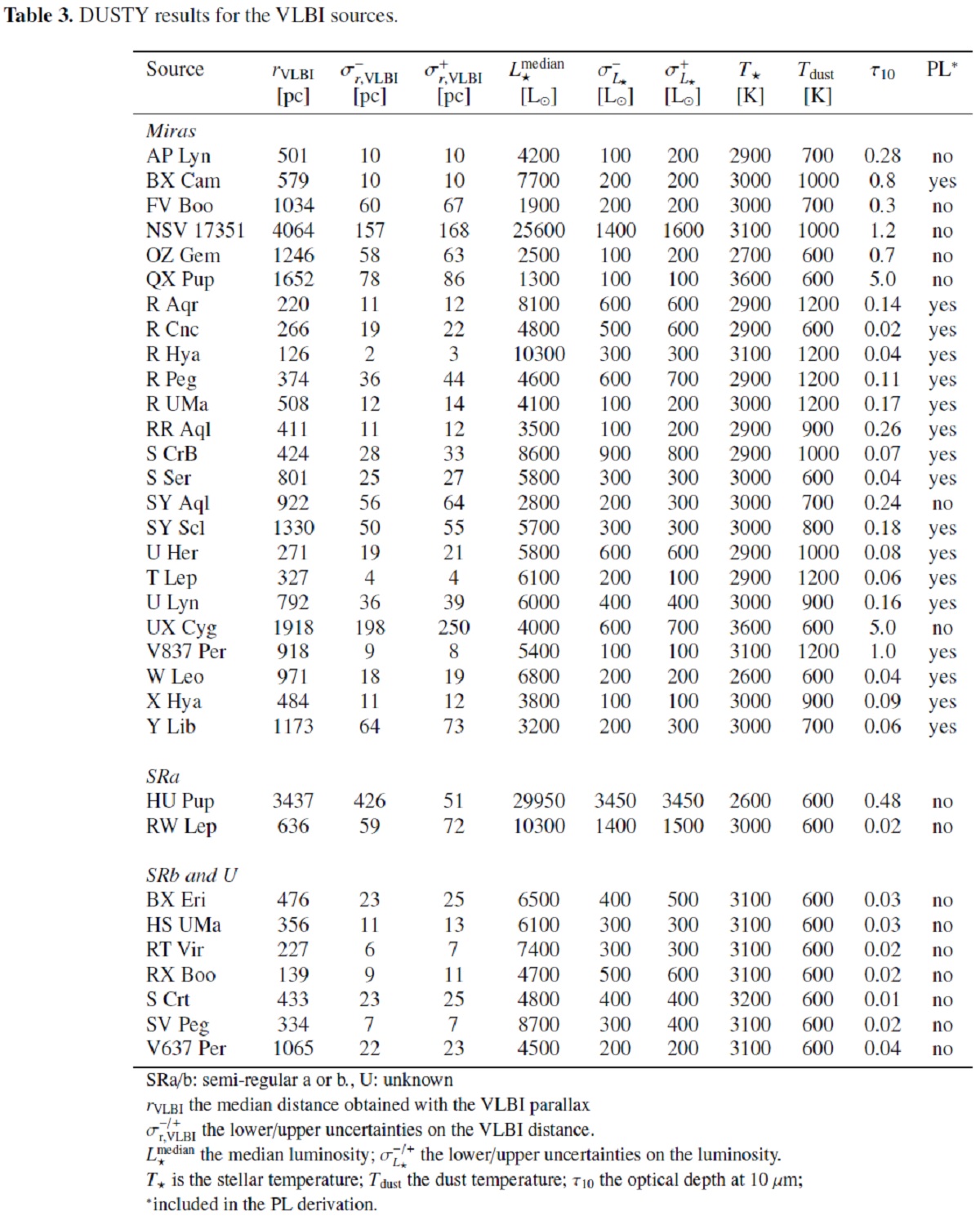
低精度星への対策 DEATHSTAR サンプルには、第4章の方法で補正視差から導いた距離が不確か 過ぎて棄却された星が多い。そこで、別法として PLR による距離推定を考え る。そのため、 VLBI サンプルを用いた新しい PLR を導く。 DUSTY VLBI サンプルの光度は SEDs に DUSTY フィットを行って求める。App B に そのやり方を述べた。表3にその結果を示す。Mbol,o = 4.74 を仮定した Mbol と GCVS または VSX から求めた周期 P を用いる。 OH/IR 星 規則的なミラ型変光 を示さない星は PLR 導出には使わない。したがって、 OH/IR 星は省かれる。 van Langrveld90 Whitelock91 は OH/IRs が PLR の下に現れることを指摘し た。VLBI サンプル中、 SIMBAD で OH/IR とされているのは NSV 17351, QX Pup, SY Aql であるが、OZ Gem Urago20 も oH/IR 星になりつつあるある星 ではないかと言われている。Chibueze20 は AP Lyn が同様の過程にあるとした。 最後に、FX Boo を Lewis20 a, b はマスロスが停まったり、始まったりする死 にかけの OH/IR 星とした。Kamezaki16 は20年間にわたる FX Boo モニター から, この星が 2005 に一時的な光度低下を経験したことを述べた。UX Cyg のメーザー強度が激しく変動することは Etoka, Le Squeren 2000 が述べている。 Whitelock08 は UX Cyg を彼らの PLR サンプルから除いた。 Whitelock PLR Whitelock08 は周期帯毎にゼロ点をずらす形式で PLR を導いた。得られた PLR の勾配は -2.67±1.88 で、ゼロ点は 2.323±4.8432 であった。エラーが大きいのはサンプル数が少ないためである。この問題は 勾配を固定してゼロ点のみを自由パラメターとすれば解決する。 LMC と MW の星を用いて、Whitelock08 は O-リッチ星と C-リッチ星の間でゼロ 点は異なるが K バンド勾配は等しいことを示した。かれらはさらに、LMC と MW の間でゼロ点は共通であるとした。 PLR のこの普遍性を使い、 Whitelock et al. (2009) は Fornax 距離を定めた。 新しい PLR そこで、K バンドでの勾配普遍則が輻射等級にも成立するとして、 我々は LMC 炭素星で Whitelock et al. (2009) が決めた勾配 -3.31±0.24 が輻射等級 PLR にも成立すると仮定し、 VLBI サンプルに対し以下の式を求めた。 Mbol = (-3.31±0.24)[log P - 2.5] + (-4.317±0.060) 今回 M-型星に定めたゼロ点は LMC C-星や(Whitelock06,09) や MW C-星 (Feast06) に対するゼロ点の範囲と大体合っている。図9を見よ。 特に得たゼロ点は Whitelock et al. (2009) の値と良く合っている。 L の評価法 Whitelock et al 2008, 2009 は Matsuura07 のDUSTY 法について、L を 最大で 50 % 高く見積もると批判した。最も逆に Whitelock らの内挿法は 両端で過小評価を招く危険がある。 |
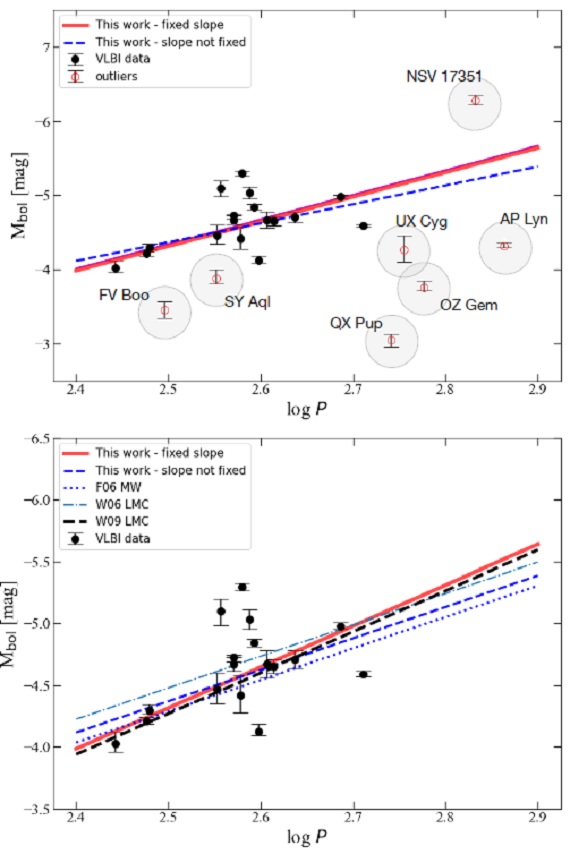 図9.ミラ型の PLR. 上:VLBI サンプルの L を用いた輻射等級 PLR. 赤実線=勾配固定で決めたフィット。青破線=勾配とゼロ点フリーの フィット。大きな白丸はフィットから除いた星。 下:炭素星に対する様々な PLRs の比較。黒点=VLBI sアンプルは上 と同じなので注意。 (下図は何を言おうとしている? ) PLR の普遍性 Urago20, Chibueze20 はPLR の普遍性に対し疑問を投げかけている。 Urago20 は OZ Gem を OH/IR 星ではないかとした。 長周期 O-リッチミラの不在 図9から MW では P > 600 d の O-リッチミラが不在である。しかしながら、LMC ではその周期の O-リッチミラが存在している。 |
|
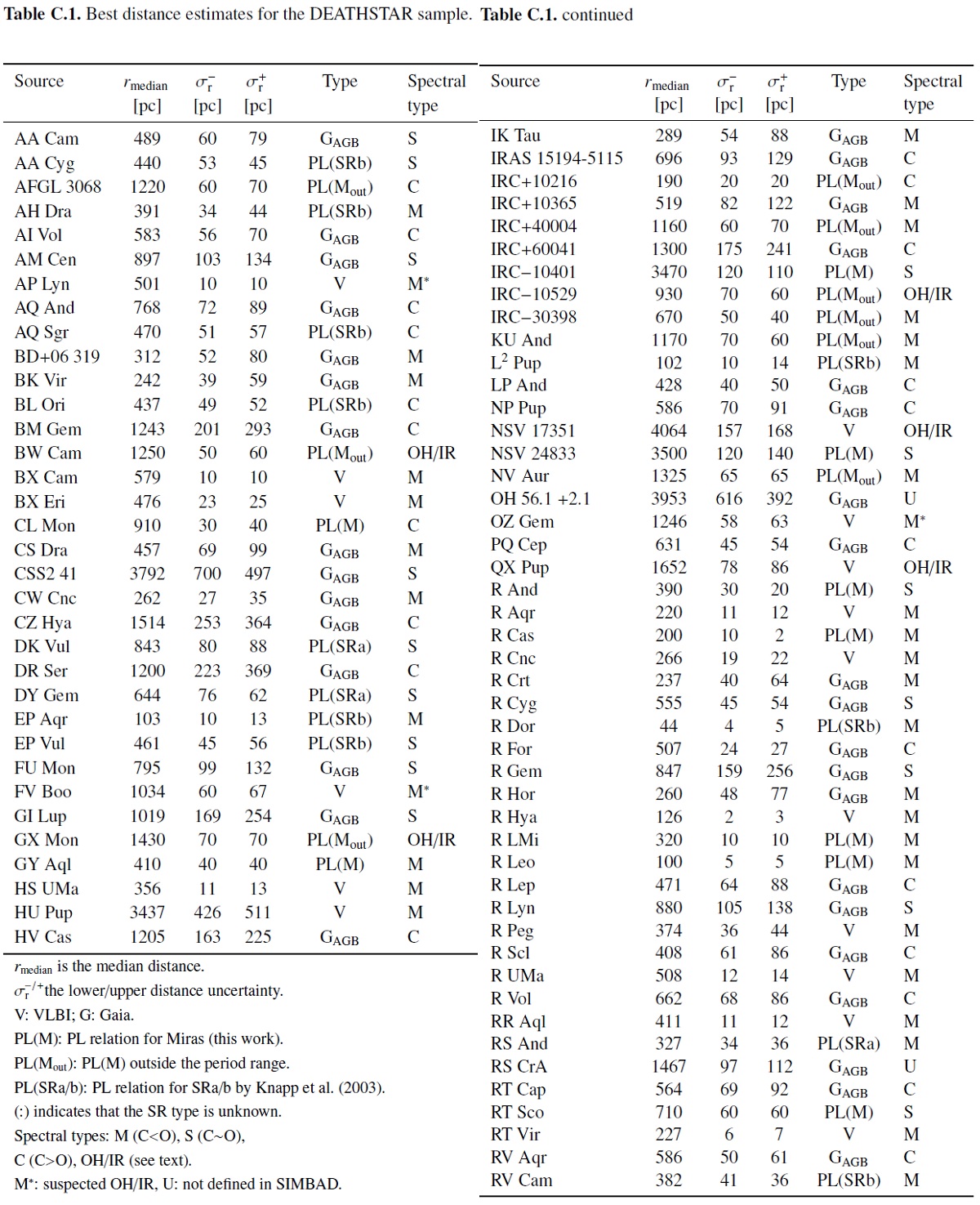
表C1にDEATHSTAR 星の新しい距離カタログを示す。 星の区分けは以下の通りである。 (i) タイプ"V" = VLBI サンプル AGB 事前確率を用いてベイジアン法で VLBI 視差から距離とその エラーを決定した。相対エラーは 25 % 以下である。 (ii) タイプ "GAGB" = 補正DR3視差相対誤差<15% AGB 事前分布を用いたベイズ推計距離。 (iii) タイプ "PL(M)" = 補正DR3視差相対誤差が 15 - 20 % ベイズ距離の相対誤差が 25 % 以下ならそれを用い、タイプは "GAGB"。それ以上で変光周期とタイプが確定していれば、 PLR を用いる。ミラ型星には Mbol = (-3.31±0.24)[logP-2.5] + (-4.417±0.060) (iv) タイプ "PL(SRa/b)" = Knapp03 の SR PLR は MK = -1.34(±0.06)logP - 4.5(±0.35) |
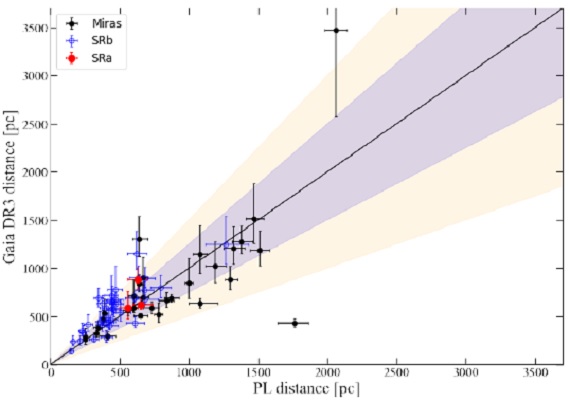 図10."good" Gaia Dr3 距離と PL 距離の比較。青線= ± 25 %. 橙線= ± 50 %. |
NESS |
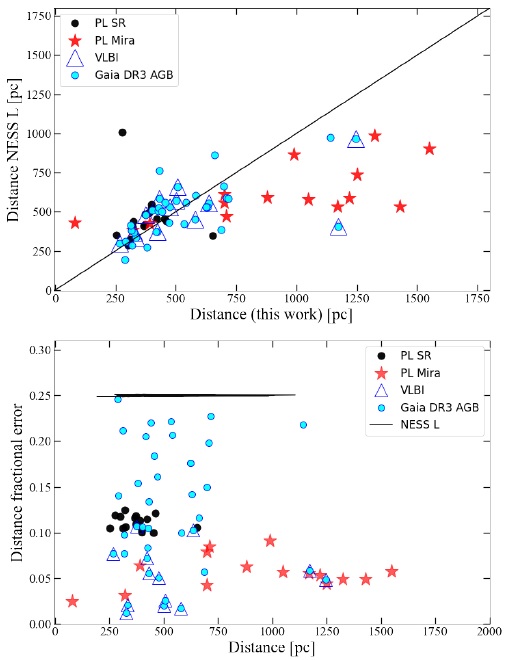 図11.上:NESS 光度距離と今回決めた距離の比較。下:今回とNESS 光度 距離の距離相対誤差 |
RUWE |
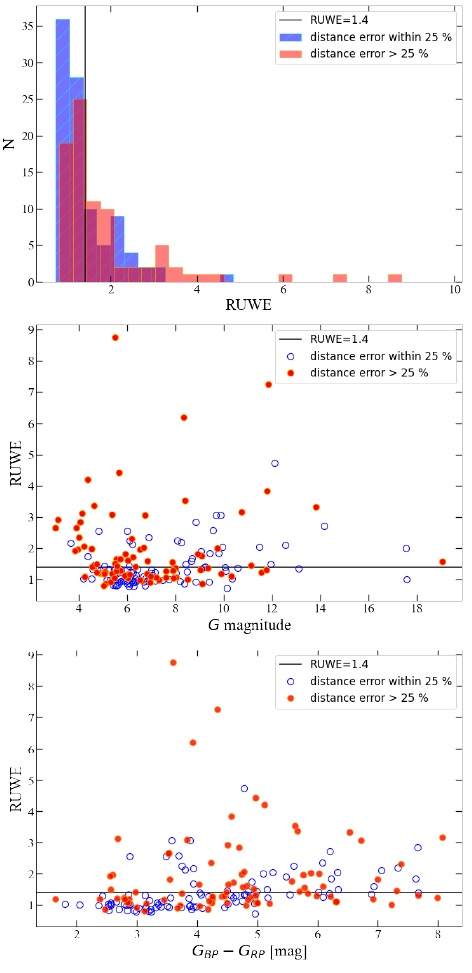 図12.上:DEATHSTAR サンプル星の RUWE 分布。青=DR3距離相対誤差 < 25 %、"good". 赤=DR3距離相対誤差 > 25 %、"bad". 中:G 等級と RUWE の関係。下:カラーと RUWE の関係。 |

|
大きなノイズ Gaia の AGBs 視差は、星周ダスト、大きな半径、表面輝度の変動、などに よって大きなエラーを含むことが示された。Chiavassa18, Xu19, El-Badry21. VLBI 視差との比較から G < 8 mag の AGBs に対しては、Gaia DR3 視差 の標準エラーはファクター5以上も過小評価されていることが判った。 Gaia DR2 で行われた "astrometric excess noise" の導入は不定性を過大 評価する結果となる。DEATHSTAR と VLBI サンプル星の 60 % 以上に対し。 DR3 の過大ノイズは DR2 の過大ノイズより大きい。 ベイズ推計法 Bailer-Jones15 のベイズ推計法に従い、DR3 視差から距離を推定した。 この方法は距離分布の情報を与える事前確率を必要とする。この論文では Jura, Kleinmann 1990 の銀河系 AGBs 分布則を採用した。この方法で最も 大事なパラメターは測定視差の相対誤差である。我々の結果は Bailer-Jones15 が良い精度の測定に対して与えた精度限界 0.2 より大きな限界値を導いた。 この限界値より小さな相対誤差では、距離の事後分布は測定値の尤度分布に 接近し、距離は 1/ω になる。そのような例は VLBI サンプルの殆どと DEATHSTAR サンプルの半数以上の星で見られた。残りの相対誤差が 0.2 以上 の星では事後確率分布は事前確率分布に支配され、距離エラーは大きく、非 対称である。その際の距離不定性は大きく、 1/ω に近くなりそうにない。 |
距離カタログ VLBI 天体に DUSTY フィットを行い、VLBI 視差を用いて光度を決定した。 それから銀河系 O-リッチミラの PLR (P = 276 - 514 d) Mbol = (-3.33&plumn;0.24)[logP-0.24] + (-4.317&plumn;0.060) を求めた。この PLR は LMC, MW の炭素星 PLR と有意には違わない。 距離カタログ 約 200 の近傍 AGB 星に対し、 VLBI, 補正 Gaia DR3 視差、PLR から定めた距離のカタログを作成した。 RUWE の注意 RUWE < 1.4 の星は注意する必要がある。 |