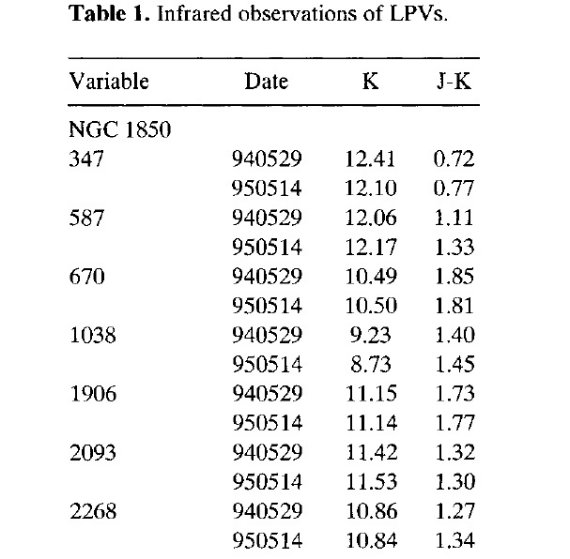
表1a.NGC 1850付近(?)の LPV 赤外観測
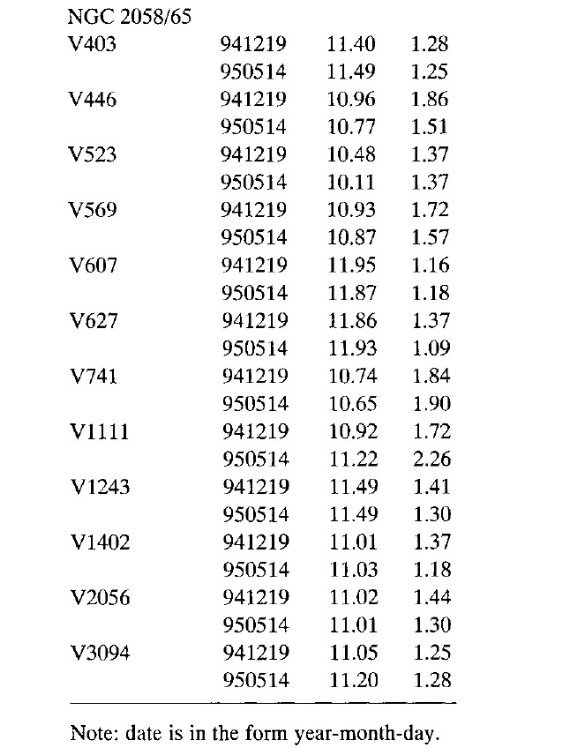
表1b.NGC 2058/65 付近(?)の LPV 赤外観測
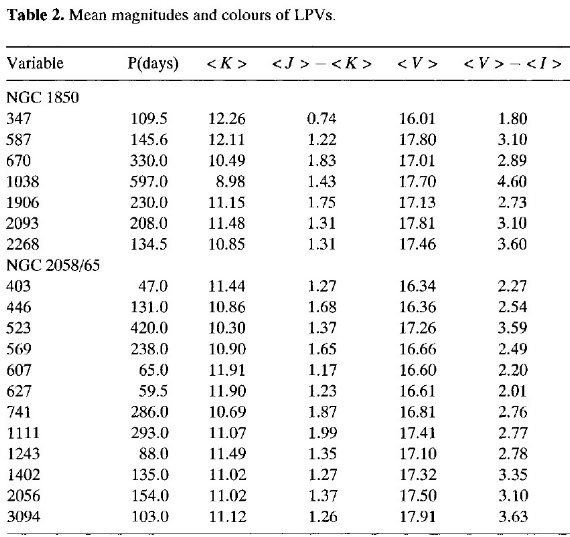
表2.LPV の平均等級とカラー
| ミラ型変光星の視直径測定はこれらの星が非常に大きくて、基本振動よりは 第1倍音振動と合致することを示している。一方では、ミラ型星の非線形脈動 モデルは、少なくとも M ≤ 2 Mo 星に関しては、観測されるような大きな 速度振幅を達成できるのは基本振動だけであることを示す。ここでは、LMC の LPV が二本の (K, log P) 系列に乗ることを示す。一本は良く知られたミラ 系列で、もう一本はそれと平行する Δlog P = 0.35 の系列である。 ミラ系列上の LPV 振幅は ΔI = [0.1, 3] という大きな散らばりを持つ。 第2系列の振幅は ΔI < 0.5 と小さい。ΔI > 0.5 の 既知 LPV は全て第1系列に乗る。 | LPV の理論モデルは基本振動周期の第1、第2倍音周期に対する比として、 Δlog P = 0.3 - 0.4 を予想し、かつ倍音振幅は基本振動よりも小さな 極限振幅を持つことを予想する。もし、第1系列が基本振動で、第2系列が 倍音ならば、観測結果は自然に理解できる。第2のテストとして、 LMC の 古い巨星枝にある星に対して振動モデルを計算し、計算された周期を観測と 比較した。基本振動脈動星の周期は観測されたミラ型星と一致した。倍音周期 はミラ型星周期には短すぎた。これらの結果はミラ型星が基本振動という説を を強く支持する。 |
|
基本振動か第1倍音か ミラの振動モードを説得力を持って定める事は未だになされていない。ミラ のような赤色巨星では基本振動周期と第1倍音周期の比は2より大きい (Fox, Wood 1982) ことを考えるとこれは驚きである。ミラの質量と半径を 適当な方法で決めさえすれば、最初の数モードに対する理論的な周期・質量・ 半径関係と比較して、振動モードを決めることが出来るはずだ。このような 解析は過去に多くのしごとがある:Wood 1975a, 1990b, Whitelock 1986, Tuthill et al 1994, Haniff,Scholz,Tuthill 1995, Feast (1996) などがそれである。周期数百日のミラの運動学的性質は古い円盤種族 Feast (1963), Jura, Kleinmann 1992 と一致することから、ミラの質量として通常 1 Mo が 仮定される。半径は直接視直径を測定するか、温度スケールを仲立ちにして 有効温度から決める。これらの研究は一般にミラは第1倍音モードで振動して いるという説を支持している。ただし、非変光赤色巨星のもっと暖かい温度 スケールを採用すれば、ミラが基本モードで振動するという説も成り立つ。 第1倍音説の大きな難点 しかし、第1倍音説には大きな難点がある。第1倍音振動星の半径は非常に 大きいので、重力が小さく、脈動速度が観測される速度よりずっと小さくなっ てしまう Hill, Willson 1979, Willson 1982, Bowen 1988, Wood 1990a, Bessell, Scholz, Wood 1996 のである。ただし、ここでも状況はあいまいで、 M ≥ 2 Mo か P ≤ 250 d の第1倍音モデルは観測される速度振幅と 一致する。Wood 1974, Tuchman 1991. 基本的に言って、問題の根源はミラの半径を決める困難さにある。その大気は 非常に広がって、次第に星間物質に溶け込んでいき、境界を決めにくいのであ る。 |
二本の系列の間隔 赤色巨星脈動モデルによると、星が AGB を昇って行くと倍音モードが不安定 になる。最も不安定なモードは光度が上がるにつれて低次になっていき、AGB 先端では基本振動が最不安定となる。(Fox, Wood 1982) もし、ミラが基本 振動星であるなら、LMC の (K, log P) 図中に Δlog P = 0.34 離れた 二本の系列が見えるはずである。なぜなら、P0/P1 = 2.2 だからである。一方、もしミラが第1倍音振動星なら P1/P2 = 1.3 に対応して、Δlog P = 0.11 くらい にしかならないだろう。 CCD で小振幅 LPV を発見 LMC 星団の CCD 観測は多数の LPV を発見した。以前の写真観測では振幅の 大きな、例えば Hughes 1989 は ΔI > 0.5 を LPV とした、変光しか 検出できなかった。しかし、新しく発見された LPV は既知 LPV に較べ振幅が 小さい。この論文では新しく発見された LMC LPV 中に第2の K-logP 系列を 探す。振幅が小さいことから、それらがミラより高次のモードで振動している 可能性は高い。 以前の試み Wood 1975b, Barthes, Tuchman 1994 は以前に太陽近傍のミラの 変光曲線中に多重モードの存在を探した。しかし振幅の大きな振動星中に 第2モードを検出することは失敗に終わった。 第2の方法 第2の方法として、大振幅振動が開始される光度より暗い所で、理論モデル を巨星枝にフィットする。次にそれをミラ領域に伸ばし、モデルを LMC ミラ の観測と較べるという方法がある。Wood 1995 に予備的結果がある。 |
 表1a.NGC 1850付近(?)の LPV 赤外観測  表1b.NGC 2058/65 付近(?)の LPV 赤外観測 |
この研究で用いる LPV は、(1)LMC 星団 NGC 1850 = LMC バー北端付近
と、(2)NGC 2058, NGC 2065 = LMC バー南端付近、で発見された。赤外撮像
観測は 1994 May 29 と 1995 May 14 に行った。また、単素子赤外観測が 1994
Dec 19 に 10 arcsec アパーチャで行われた。表1に観測を、表2にはその
平均を載せた。
 表2.LPV の平均等級とカラー |
|
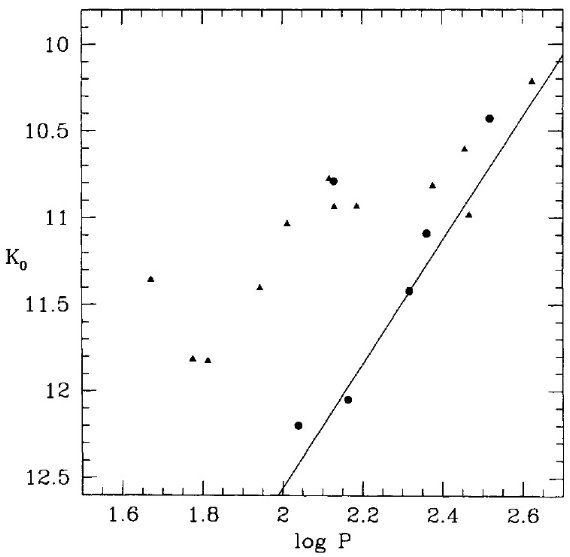
図1= Ko - log P 関係 図1には観測された Ko - log P 関係を示す。E(B-V)NGC1850 = 0.15, E(B-V)NGC2058/65 = 0.21 を仮定した。A(K) = 0.4E(B-V) とした。 第2系列 図1を見ると、 LMC ミラ系列にあるのは LPV の半数である。図1には明ら かに第2の系列が見られる。それは第1系列と平行し、ΔlogP = -0.35 離れている。同じ光度での周期の比では 2.2 に当たる。この値は第1節で議論 した値 2.1 に驚くほどに近い。従って我々は、ミラ系列は基本モード、第2 系列を第1倍音モードと考える。 図1.LPV の Ko - log P 関係。丸= NGC 1850 付近の星。三角= NGC 2058/56 付近の星。実線= LMC ミラの関係 (Feast et al 1989). |
 |
|
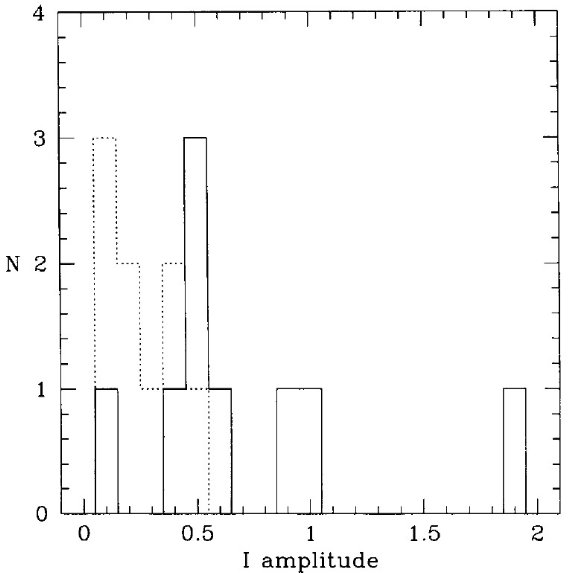
図2=振幅分布 一般的に倍音振動は基本振動に較べ振幅が小さいと考えられる。そこで、 図2に二つの系列に属する星の振幅 ΔI の分布を示した。ミラ系列の振 幅は ΔI = [0.1, 2.0] に亘るが、大部分は ΔI ≥ 0.5 である。 一方、ΔI ≤ 0.5 に限られる。 図2.I 等級振幅の分布ヒストグラム。実線=ミラ系列。点線=第2系列。 |
 |
| 図3に NGC 1850 周り、10'x10' の星の (I, V-I) 図を示す。黒丸=NGC 1850 周りの LPV。黒三角= NGC 2058/2065 周りの LPV. M = 0.8(破線), 1.0(実線), 1.5(点線) Mo の理論 AGB 経路も示す。0.8 Mo はコアマス=0.6 Mo になる質量、 1.5 Mo は 3 Gyr 昔に始まった星形成バースト(Butcher 1977, Bertelli et al 1994) に対応する。質量と光度の組に対し、光度・核質量関係 Wood, Zarro (1981) で核質量を定め、外層部のモデルを計算する。混合距離 l は Mbol = -1, MI = -2.5 の AGB 下部で正しい有効温度を与えるように定めた。 l/HP = 2.5 が最適値であった。この l/HP で AGB 上部 まで計算を進める。(L, Teff) から (MI, V-I) への変換には、 Teff > 4000K では Kurucz 1993 のモデル大気を用いた。より低温では、 Bessell 1979 の (V-I, logTeff) 較正と、Bessell, Wood 1984 の BCI を用いた。この手法で LPV の温度スケールを考えずに済んだ。LPV の温度と半径 は、混合距離比 l/HP 一定の仮定から直接導かれた。この仮定は 一般に、例えば球状星団の巨星枝を上手く再現した。AGB 系列のためには、OPAL オパシティ(Iglesias, Rogers 1993) が用いられ、そこに Chios, Wood, Capitanio 1993 の分子オパシティが加えられた。Y = 0.30, Z = 0.008 を用いた。 |
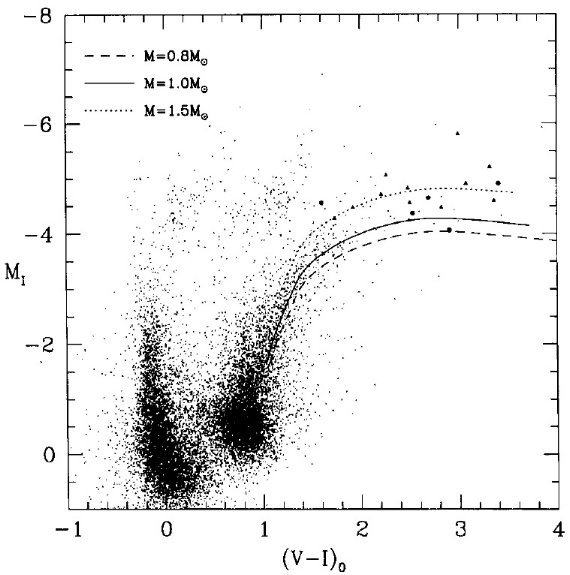 図3.NGC 1850 周り、10'x10' の星の (I, V-I) 図。黒丸=NGC 1850 周りの LPV。黒三角= NGC 2058/2065 周りの LPV. M = 0.8(破線), 1.0(実線), 1.5(点線) Mo の理論 AGB 経路も示す。 |
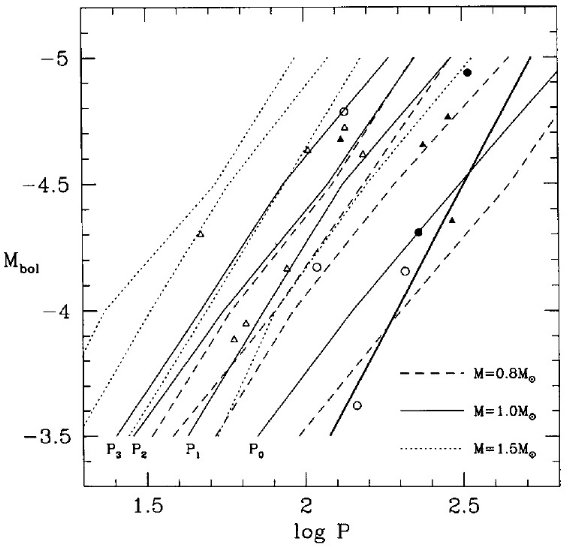
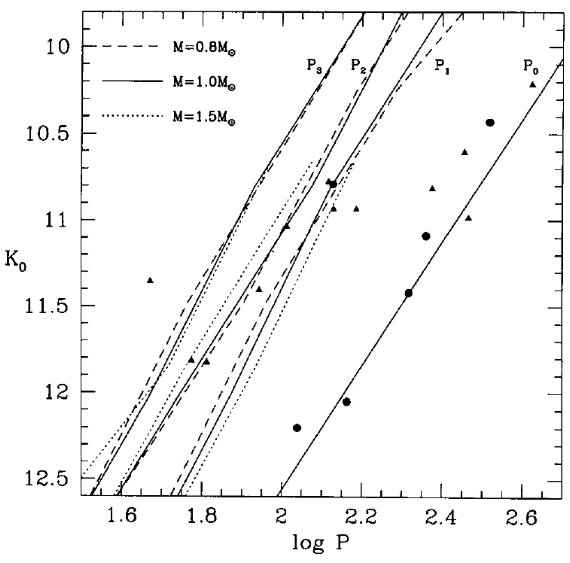 図4.(Ko, log P) 面上で観測 LPV とモデルとの比較。点の意味は図1と同じ。 基本振動モデルは Feast et al 1989 に合うように強制した。そして、モデル 周期比を用いて、第1倍音、第2倍音、第3倍音ラインを引いた。 線形非断熱動径振動 図3の AGB モデルに対し、 Fox,Wood 1982 の方法に先に述べた新たなオパ シティを加えて、線形非断熱動径振動を計算した。これらを観測結果と比較する ために二つの方法を用いた。 |
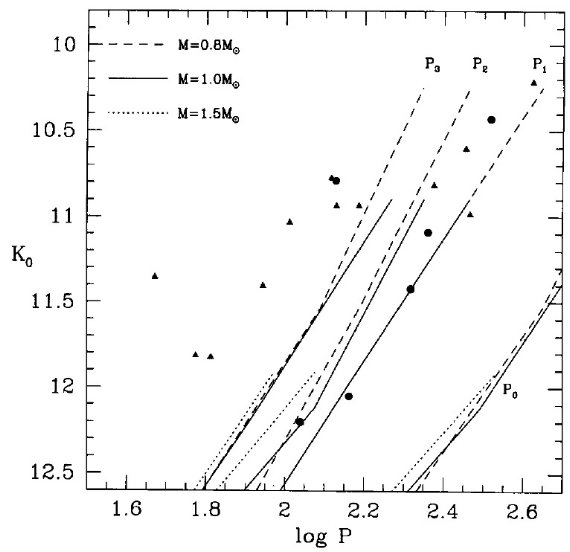 図5.図4と同じだが、ミラ系列に第一倍音を強制的に合わせた。 第1の比較法 第1の方法では、モデルで得られるモード間の周期比を用いる。しかし、 周期自体は用いない。 この方法は混合距離比 l/HP が巨星枝を昇る 際に変化して、距離比一定では不正確な Teff を、さらに不正確な周期を 与える可能性を避けることができる。周期比は星のパラメタ―に鈍感なので 比較的安全である。そこで、与えられた K 等級に対する振動モデルの基本振動 周期を観測値に変え、周期比はモデル値を使って、倍音の周期を計算する。 その結果を図4に示す。同様の処理を、第1倍音を使って行った結果が図5 である。図4の方が観測と合う。 |
|
第2の方法 この方法では、モデルで決まる基本、第1、第2、第3倍音の4つの周期を 0.8, 1.0, 1.5 Mo に対して直接プロットした。AGB 星モデルは前と同じ である。図6にその結果を示す。 光度と共に質量が増せばよい。 図6を見ると、ミラの周期光度関係は、光度が上がると共に、質量が上がると 考えれば、基本振動でうまく説明できることが判る。 銀河系ミラの運動と年齢 Feast (1963), Jura, Kleinmann (1992a) は銀河系ミラ型星の運動学的性質から、周期と共に質量が増加することを 示した。ここで見つかった第2系列の星は倍音系列として説明できる。 図6.質量 0.8, 1.0, 1.5 Mo の基本、第1、第2、第3倍音の周期と光度 の関係。太い実線= LMC ミラ (Feast et al 1998). 丸= NGC 1850 付近の LPV. 三角= NGC 2058/2065 付近の LPV. 白印= M-型星。黒印=炭素星。 |
 |
| LMC の小振幅と大振幅の LPV を赤外で観測した。それらは、K-logP 面上で 二つの系列に分かれた。一つはミラ型星系列で、第2系列はミラ系列と平行だ が、周期が 2.2 倍小さい。理論振動モデルとの比較から、ミラ系列は 基本振動で、第2系列は倍音と考えられる。 | ミラに対して、視直径の観測、または Teff の観測から得られた大きな半径 には説明が必要である。可能な説明としては、ミラ距離を過大に見積もってい る、大気オパシティを過小評価、脈動によるミラの膨張などがある。 この問題の理解は明らかに必要である。 |