2.有効温度とカラー
二つの Te - (J-K) 関係Te - (J-K) 関係に二つの意見があった。この二つは殆ど同じ勾配 dlogTe/d(J-K) ∼ -0.21 (Feast et al. 1989) を持つが、ゼロ点が 0.1 異なる。 もう一つの方 Wood et al 1991 は主に月掩蔽から決められた非ミラ型星の角直径から 導かれた。かれらの関係の勾配は高温側はやや早期型の星、低温側は炭素星の観測 から決められた(Bessell, Wood, LoydEvans 1983)。
炭素星使用への疑問
したがって、ミラやSRの領域 での関係は炭素星の結果に強く依存する。しかし、炭素星とM型星とはオパシティが 異なるので、適用可能性に疑問が残る。
さらに、炭素星はしばしば周囲にダストシェルを有しこれがカラーに影響する。しかし、 もしわれわれが炭素星の結果を無視すると、(J-K) - logTe 関係の勾配が低温度 領域で決められなくなる。
黒体温度の適用範囲
良く使われる他の関係式ではミラの角直径の観測に基づいたゼロ点を有している。 この様にして決めたミラの有効温度は赤外SEDに黒体フィット(TBB) して決めた温度 (Roberts,Feast 1981, Glass,Feast 1982)と近い。この関係の 勾配は dlogTBB/d(J-K) (Feast et al 1989) から決められる。しかし、 Te ∼ TBB はある限られた温度領域でのみ角直径測定により 確認されているだけであり、 dlogTBB/d(J-K) = dlogTe/d(J-K) の観測的証拠とは言えない。
早期型の角直径測定の例はないのか?やっぱり、黒体フィット の有用性はチェックしておきたいな。
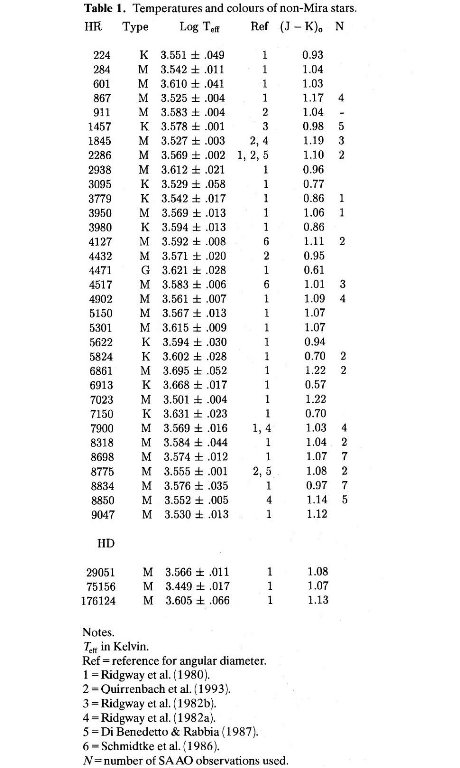
角直径データ
表1,2に酸素型のミラと非ミラに対し、(J-K) - Te 関係を調べるための データを集めた。Te は角測定に依存する。ミラと非ミラの双方で 2 μm での 直径を「真の」直径と考える。この論文の中では脈動関係式に使われる半径という 意味である。非ミラでは角直径は波長によってあまり変化しない。しかし、ミラでは 大気が広がっているため波長で大きく変化する。赤波長域で得られた角度は大気モデル を使って「真の」角直径に直された。このデータと輻射等級とから Te が導かれる。 非ミラでは Te は表2にある文献から採られた。ミラに対しては新しい mbol が、公刊されたデータ、または SAAO JHKL 測光から求められた。大部分 の場合、ミラの測光データは角測定と類似の変光位相での値である。
Ridgway et al 1992 は 2 μm で散乱光のため、見かけ直径が大きくなると 述べた。しかし、その効果を入れないでも観測とモデルが良く合うことから 考えると、この効果は小さいのではないか?
測光データ
可能な限り SAAO データを使った。SAAOの二つの赤外装置の間の関係は、 (J-K)1.9 = 0.955 (J-K)0.75 である。赤化補正は 通常は必要ないが、Feast, Whitelock,Carter 1990 にある手続きに従った。 SAAO データのない非ミラは Ridgway et al 1980 に 0.073 を Carter (0.75) システムに加え、次に 1.9m システムに変換して用いた。

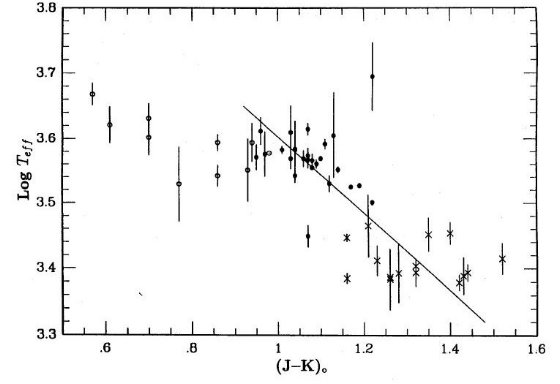
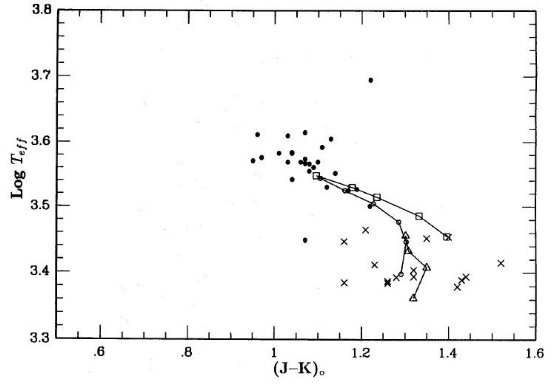
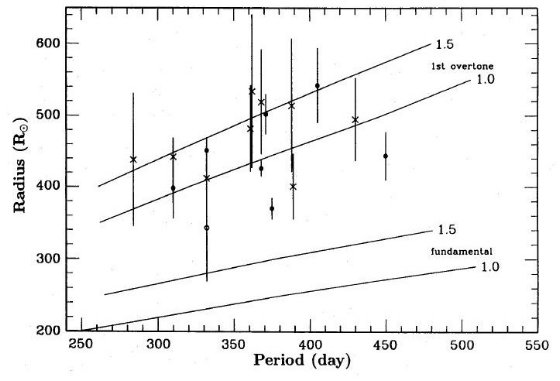
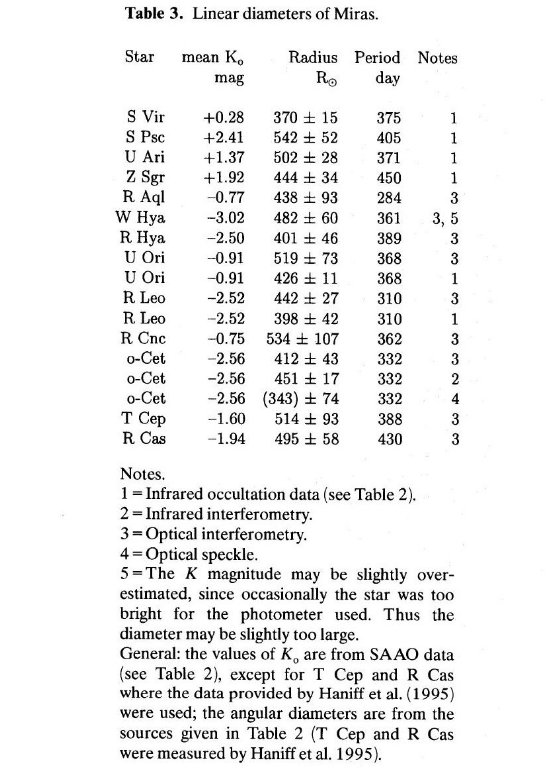
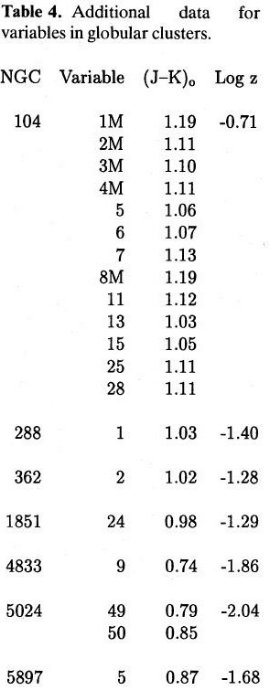
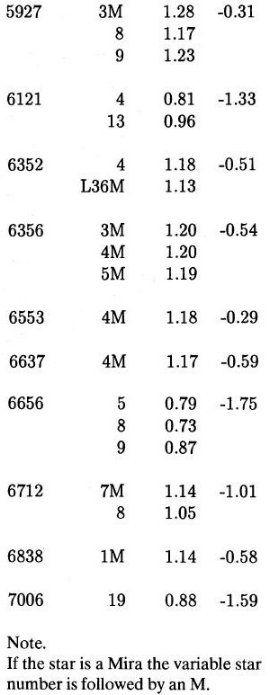
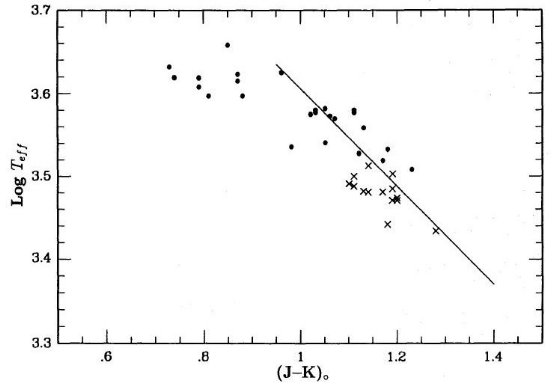 図4.式(9)から決めた球状星団内SR,ミラの Te
図4.式(9)から決めた球状星団内SR,ミラの Te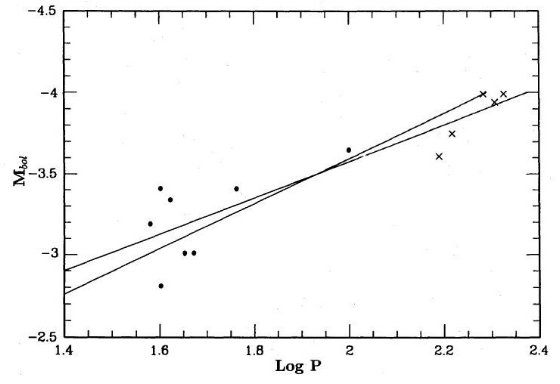 図5.47 Tuc 内SR、ミラの Mbol - log P プロット。回帰線も示す。
図5.47 Tuc 内SR、ミラの Mbol - log P プロット。回帰線も示す。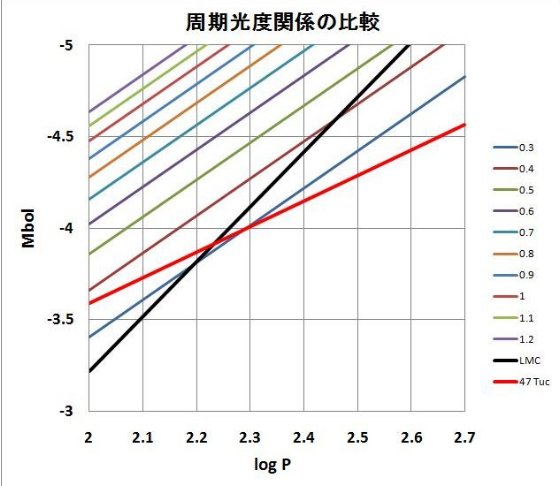 図 式(8)をlog z = -0.6, Q=0.04, でM = 0.3 - 1.2 M๏
に対し、P−L 関係。
図 式(8)をlog z = -0.6, Q=0.04, でM = 0.3 - 1.2 M๏
に対し、P−L 関係。