Wood81

Helium-Shell Flashing in Low-Mass Stars and Period Changes in Mira Variables

Wood, Zarro

1981 ApJ 247, 247 - 256

　アブストラクト　

　M = 0.8, 1.0, 2.0, 3.0 Mo で、Mc = 0.53 - 0.9 Mo の星でのヘリウムシェルフラッシュを調べた。特に注意したのはフラッシュ後の光度変動である。というのは、フラッシュサイクル中の表面光度の極大は AGB 進化の終焉を決めるのに重要だからである。フラッシュ期の光度ピーク L_P と静謐光度極大 L_Q　の双方はコア質量に比例して増加する。

　L_P と L_Q は、大気対流層は星の内部深くまでは浸透しないから、星質量に独立である。L_P, L_Q, パルス間隔、フラッシュ期に表面光度が静謐期光度を上回る期間の長さが M_C にどう依存するかを調べた。表面光度変化の近似式も与えた。ミラ型星、 R Hya, R Aql, W Dra の周期変化をモデルと比較した。その結果、光度と光度変化率の関係から光度に制約が与えられた。こうして求まった、R Hya, R Aql の光度を脈動モデルから求めた光度と比較した。

　１．イントロダクション　

　AGB 終焉の二つの説　

　AGB の終焉として次の二つが唱えられている。

１．水素層の質量が徐々に減少し、 0.002 Mo で終わる。
　　　　　(Kwok, Purton, Fitzgerald 1978)

２．急速な質量放出。その原因として、力学的不安定性 Lucy 1967, Paczynski, Ziolkowski 1968, Roxburg 1967.
基本振動脈動に伴う緩和振動。Smith, Rose 1972, Wood 1974, Tuchman, Sack, Barkat 1979.
輻射圧による全外層の放出。Faulkner 1970, Sparks, Kutter 1972.

第１メカニズムでは長い静謐期のマスロスが重要である。第２メカニズムは一般に光度がある臨界値を超えた時に起こる。従って、もしシェルフラッシュの時の表面光度がフラッシュ直前の静謐期光度極大を超えるなら、フラッシュのピーク光度期に急激なマスロスが起きるかも知れない。

　ＡＧＢ進化の二つのシナリオ　

　AGB 進化のシナリオを考えるに際し、 Wood, Cahn (1977) はフラッシュピーク光度は静謐期光度極大を下回ると考えた。一方、 Tuchman, Sack, Barkart 1979 は上回るとした。この二つのどちらが正しいかによって、進化の様子は大きく変わる。この論文では、シェルフラッシュ期の変更を体系的に調べ、どちらが正しいかを調べる。

　２．計算　

　計算不安定を避けるため、エネルギー流を層境界でなく、層中心で定義してヘニエコードで計算した。各シリーズで計算開始時には、水素欠乏核と外層の質量を与えた。

　最初に人為的に水素燃焼殻とヘリウム燃焼殻の間の質量を多めにしておく。するとヘリウム燃焼が盛んになり、やがて小さな振動が開始され、大体１５回くらいで本格的なシェルフラッシュを起こす。　

　３．計算結果　

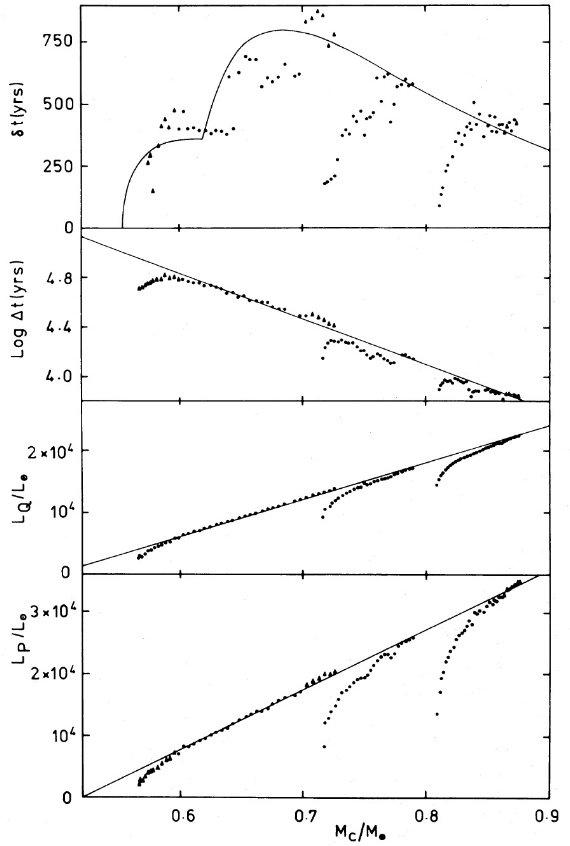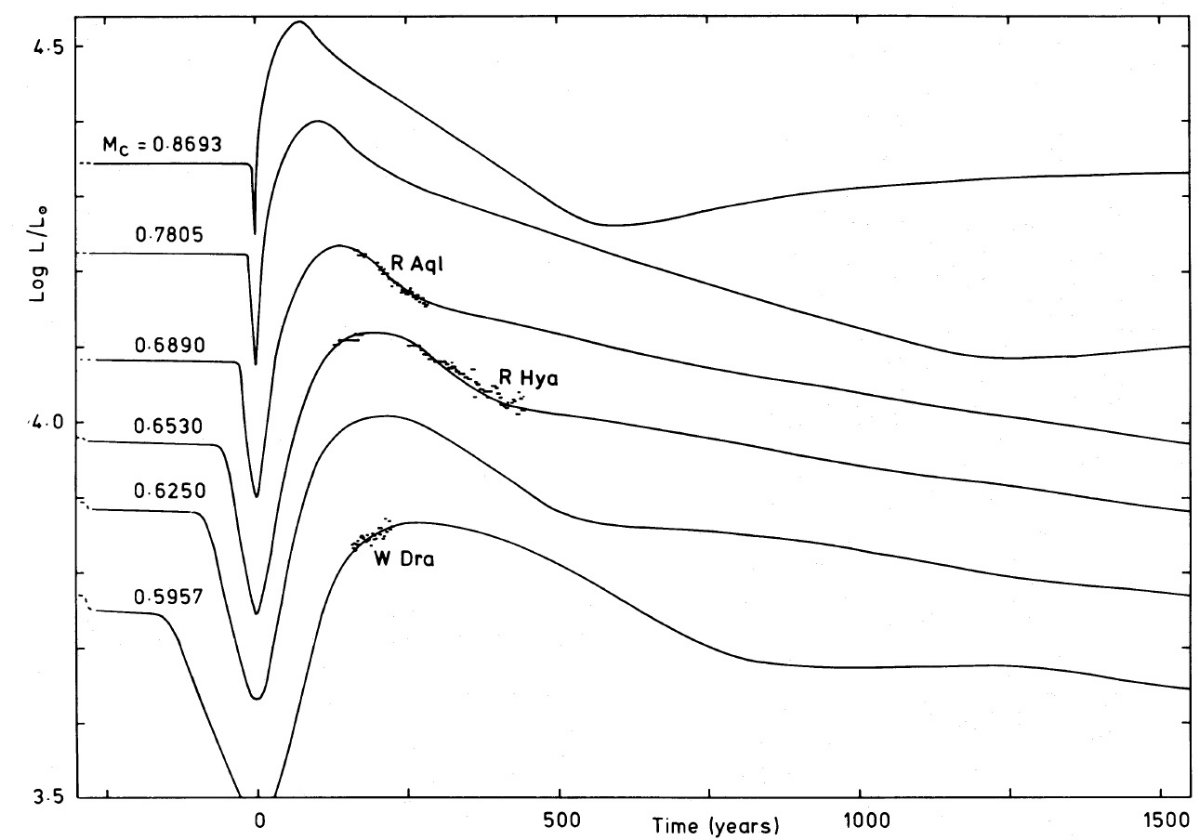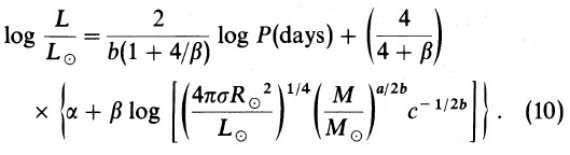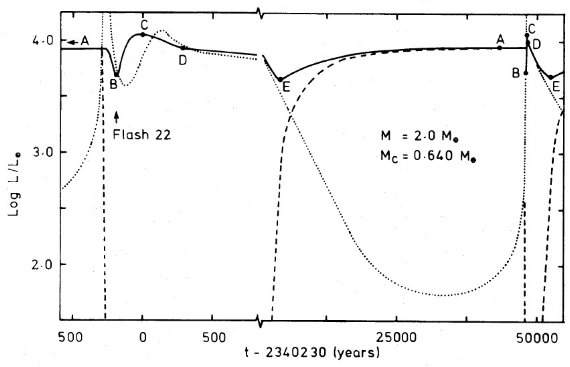
図１．フラッシュ期間中の、実線＝表面光度変化、破線＝水素燃焼光度、点線＝ヘリウム燃焼光度。

　３．a. 典型的フラッシュでの表面光度変化　
　図１に表面光度変化を示す。熱サイクルの静謐期は水素燃焼が主で、表面光度は次第に上がって行く。Ａ点＝フラッシュ直前の光度静謐期極大。フラッシュが開始すると、水素燃焼が消え、表面光度が急低下する。（図１を見ると５０年くらいで底＝Ｂ点に達する。）Ｂ点でヘリウム燃焼のエネルギーが表面まで辿りつき、フラッシュのエネルギーが到達する結果表面光度は極大＝Ｃ点まで上がる。フラッシュの熱が拡散する結果点Ｄまでは光度は比較的高い状態を維持するが、その後はヘリウム燃焼の落ち込みの結果Ｅ点まで光度低下する。Ｅ点から先は水素燃焼が主なエネルギーの担い手となる。

　３．b. フラッシュの振る舞いの総質量による変化　
　熱的タイムスケール　

　ここで考えている 1 - 3 Mo の星では外層質量が 2.4 Mo 以下で、その熱的タイムスケールは数年である。
(そんなに短いのか？ダイナミカルタイムスケールとあまり変わらなくなる。一方で Menv*T/L とすると, Menv*T は太陽とあまり変わらず、L は 5000Lo とすると確かに熱的タイムスケールは太陽の 4　桁下になる。赤色巨星は透け透けなのか！ )
したがって、熱エネルギーの吸収 &epusilon;_g が効くのは B 点付近である。Ｂ点の深さはしたがって外層質量が大きくなると少し浅くなる。しかし、Ｃ点の高さ、Ｄ点までの振る舞いは、M < 3 Mo, Mc < 0.9 Mo では外層質量を変えてもあまり変わらない。つまり、Ｂ点付近を除き、外層は熱的、力学的平衡にある。もっと大きな外層質量の星では、外層による熱エネルギーの吸収が重要になる。

　中心核境界圧力、温度への外層質量の影響　

　水素欠乏核と対流外層の間には輻射層が存在する。そこではオパシティは電子散乱でほぼ一定である。輻射層の質量は非常に小さいので力学平衡式を解く際に Mr = Mc = 一定の近似が使える。以上で静水平衡式を積分すると、Schwarzschild 1958 にあるように、
　　　P = 16πσGMcT⁴/3κL
　　　T = βGMcμm_H/4kr
が導かれる。この輻射層の間に温度は一桁、圧力は４桁変化する。対流外層の効果は上式で書かなかった小さな積分定数に含まれる。その結果、中心核の進化は外層質量と独立に進む。

　３．ｃ. 2Mo 星におけるフラッシュ　
　３系列の計算　

　前節の結果に依れば、フラッシュ時の光度低下深さを除けば、フラッシュサイクルに伴う諸量が Mc によりどう変化するかは、総質量 M 一定で Mc を変えたフラッシュのモデル計算から分かる。図２にその結果を示す。初期中心核質量 0.53, 0.7, 0.8 Mo からスタートする３系列の進化計算を行った。どれも大体１５回の緩和フラッシュの後はコアマスに対応した定常的なフラッシュ強度に落ち着く。

　Mc - L 関係　

　図２から、以下の関係が導かれる。

　　　L_Q/Lo = 59,250(Mc/Mo - 0.495)

この関係の係数は Paczynski 1970, Uus 1970 が導いたものと等しい。ただ、定数の値が異なるので、彼らのフラッシュ抑制モデルから求めた L よりは大きい値を与える。

　Δt = フラッシュ間隔　　

　Δt も Paczynski 1975, Becker,Iben 1980 の与えた式と大体合っている。

　　　log Δt = 3.68(1.14 - Mc/Mo)

傾きが異なるが、Becker, Iben 1980 は様々な Mc で計算しているが緩和していないフラッシュも混ざっている。彼らの上枠部は成熟したフラッシュでその部分は我々の計算と一致する。

　L_P 　

　フラッシュのピーク光度 L_P は以下の式で表される。

　　　L_P/Lo = 97,000(Mc/Mo - 0.52)

また光度 L が前回の静謐光度極大 L_Q を超えている時間 δt は 400 - 800 yr である。
( L_P　と L_Q の差はどんどん大きくなるのか？等級差だとそうならないのか？)

　フラッシュ時の表面光度変化　

　図３には、フラッシュ時の表面光度変化が Mc の大きさで変わる様子を示す。

図２．個々のシェルフラッシュとコアマスの関係。L_P = フラッシュ期の光度ピーク。L_Q = 静謐光度極大。Δt = 前フラッシュからの間隔。δt = フラッシュ表面光度が前回静謐光度極大を上回る時間。実線＝本文で与えた式。

図３．様々な Mc に対するフラッシュ時の表面光度変化。周期変化から導いた R Hya, R Aql, W Dra の表面光度変化も示す。

　４．ミラの周期変化とヘリウムシェルフラッシュ　

　ミラの周期変化　

　ミラ型星の R Hya と R Aql の周期が動いていくことは昔から知られていた。 Wood 1975b はこの変化がヘリウムフラッシュに伴う光度変化に起因することを示唆した。残念ながらミラ型星の周期は常に数％の変動を持ち、さらに、期間 10 - 50 yr で突然 2 % 程度の突然の周期変化を起こす。この二つの効果により、多くのミラ型星では 100 年に及ぶ変光データがあるに拘わらず、連続的な周期変化の検出を困難にする。

　図４＝その実例　

　図４には極大日の O - C の時間変化を示す。よくデータの整った 48 ミラを調べた。その内 23 星は　100 年を越すデータがあった。図４に示すように、 R Hya と R Aql の周期が短くなる様子は明らかである。調査の結果新しく、 W Dra が周期が伸びている星として検知された。しかし、例えば T Cep のように 70 年間に亘り周期が伸びて来たのに、突然の周期変化で傾向が逆転する例もあるので、今後の観測が重要である。S Her は周期の突然の変化の例である。 T Her も突然の周期変化を起こすが、変化量は小さい。

　周期から光度への変換　

（１）脈動の関係式
　　　C = P(M/Mo)^α(R/Ro)^-β

（２）有効温度の式
　　　L = 4πσR²Teff⁴

（３）ＨＲ図の AGB を表式化
　　　log L/Lo = α - βlogTeff

上３式から、R と Teff を消去すると、与えられた M の下での、L-P 関係

が導かれる。

図４．O-C = O(観測極大日) - C(計算極大日)　と周期番号の関係。計算極大日は図中に示す一定周期を仮定して計算。 　

　５．ヘリウムフラッシュが AGB 進化シナリオに及ぼす影響　

　Tuchman, Sack, Barkart 1979 のモデル　

　 Wood, Cahn (1977) や Tuchman, Sack, Barkart 1979 のモデルでは、低質量星は AGB を上がり、途中のどこかでミラ型振動を開始し、更に光度を上げ、十分明るくなるとマスロスを開始する。ミラ脈動に伴う質量放出の範囲は、(log L/Lo, M) 面上に描けるはずである。Tuchman, Sack, Barkart 1979 の非線形脈動計算は (log L/Lo, M) 上にまず、ミラ型脈動領域を描くことを目的としていた。脈動領域を見出した後、彼らはミラ領域を通る AGB 星進化経路を用いて、ミラ型星の周期ー数密度関係の観測を再現しようとした。しかし、観測とモデルを合わせるには、全てのミラが ≥ 2 Mo と仮定する必要があった。この矛盾を解消するため、彼らは静謐期光度ではミラ帯の下にある < 2 Mo の星がヘリウムフラッシュ期にミラ帯に跳ね上げられると考えた。彼らの発見したミラ領域は全ての M に対して log L/Lo でほぼ等しい幅である。したがって、M < 2 Mo の星をミラ型域からはねるには、M が小さくなるに連れ、パルス高を上げなければならない。しかし、今回の計算はそれが誤りであることを示している。その上 Feast 1963 は観測されるミラが M ≤ 2 Mo であることを示している。

　Wood, Cahn モデル　

　Wood, Cahn モデルでは、(log L/Lo, M) 面上のミラ帯が観測的に探られた。そして、ヘリウムシェルフラッシュ極大光度が AGB 進化に及ぼす影響が無視された。(log L/Lo, M) 面内のある領域が観測される周期分布とミラの数密度を再現することが判った。この領域が本来のミラ不安定域と考えられた。しかし、今回の研究に照らすと、ミラ領域はシェルフラッシュの効果を入れて少し直されるべきであろう。Wood, Cahn モデルで考えられた質量放出ラインより log L/Lo で 0.15 高いところになる。

　６．議論と結論　

　Mc と L は M に独立な進化をする　

　この論文の主目的の一つは、ヘリウムフラッシュ極大光度期に前静謐期極大光度をどのくらい上回るかを、(M, Mc) の関数として探ることであった。 M ≤ 3 Mo の星では Mc と L の進化は M から独立していることが示された。例外はフラッシュ発生時の非常に短い極小期である。これは、燃焼殻の上に広がる輻射層の存在による。

　L_P と L_Q 　

　フラッシュピーク L_P と静謐期光度極大 L_Q は Mc と一次式関係を保って上昇する。計算で用いた (X, Z) = (0.68, 0.02) では、 Mc > 0.559 Mo で L_P > L_Q となり、Mc が大きくなると log L_P/L_Q = 0.21 に漸近する。

　変光周期の永年変化　

　R Hya と R Aql の変光周期の永年変化をヘリウムフラッシュ後の予想周期変化と較べると良い一致が見られた。

　L_P/L_Q　

　Tuchman, Sacks, Barkart 1979 は M が下がると L_P/L_Q が上がるという、我々と反対の結果を出した。これは、一つには彼らが Z = 0.001 モデルを使ったことではないか。 Z が下がると L_P が上がり、 L_Q は下がる。その他の多くのモデル計算とも比較した。