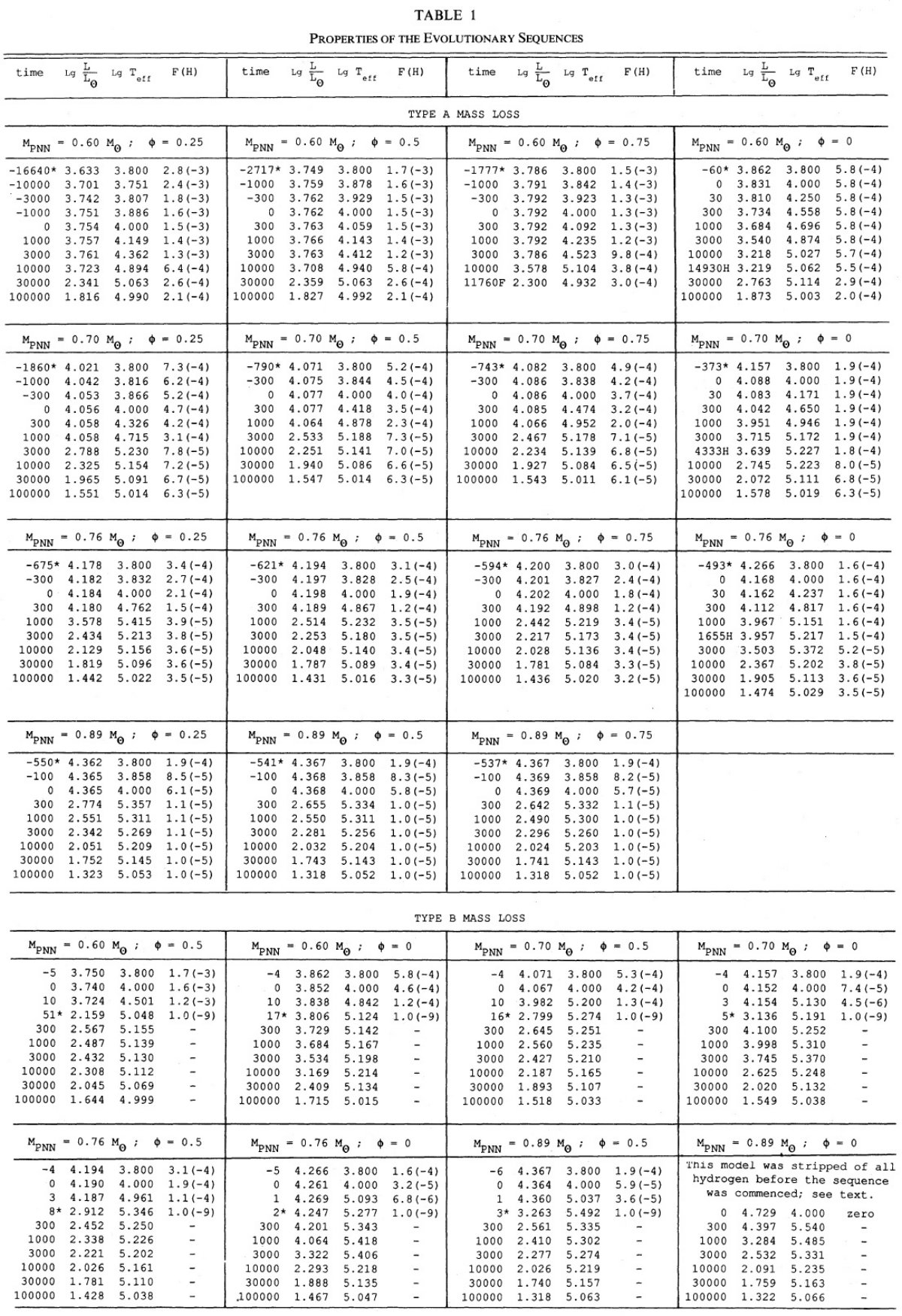
| 惑星状星雲注進星=PNNの進化を計算した。核の性質を次の3つの関数として 調べた:(1)核質量=0.60, 0.70, 0.76, 0.89 Mo. (2) AGB を離れる時の ヘリウムシェルフラッシュサイクルにおける位相 ψ = 等間隔で4種。(3) マスロス。AGB 核質量と PNN 質量には臨界値があり、それ以上では輻射圧が 高水素外層を全て吹き飛ばしてしまう。 Mc > 0.86 Mo となる AGB 星は 高ヘリウム核を持つ惑星状星雲を形成する。そのような中心核はヘリウムを燃 やしながら、PN 期を過ごし、その後冷えて non-DA 白色矮星となる。輻射圧 メカニズムはマゼラン雲の最近のサーベイで明らかになった高光度 AGB 星の 不足を説明する助けになるかも知れない。 | それより質量が小さい星で、フラッシュ間期に AGB を離れる場合には、AGB から 惑星状星雲領域に移行するまでの遷移時間は、フラッシュサイクルのどの位相で AGBから離れるかで大きく変動する。 AGB 質量放出は星がフラッシュ後の光度 極小になった時に停止するが、その後の星雲の post-AGB 膨張期の大きな割合は この遷移期間で占められる。 我々の進化計算の結果と観測データとの比較を行った。最近の惑星状星雲中心核 の光度評価には系統的にファクター3程度の過小評価が見られるという強い証拠 がある。惑星状星雲の中心核質量は 0.6 Mo - 0.8 Mo 以上に亘る。惑星状星雲は 主にヘリウムシェルフラッシュの際に放出されるという仮説に対して、観測からは 何とも言えない。 |
|
Paczynski 1971 モデル Paczynski 1971 は AGB - PNN 進化系列を 3 本計算した。彼のモデルの スタート点は、ヘリウムフラッシュを抑えた 3 Mo 星の AGB 計算から 0.6, 0.8, 1.2 Mo のコアを選び、それぞれに 1.2 10-3 Mo, 1.4 10-4 Mo, 4 10-6 Mo の高水素外層を加えた。 これらの外層質量は小さいので、スタート点は AGB から離れた所、log Teff = 4.2 - 4.7, となる. Paczynski 1971 はそこからマスロスなしで白色矮星 までの進化を計算した。3本の進化系列のどれも PNN 期間中にヘリウムシェル フラッシュが起きた。このモデルの欠点は、スタート前のシェルフラッシュを 考慮していないことである。その結果、PNN の光度低下タイムスケールに大き なエラーが生じた。 Harm, Schwarzschild 1975 モデル Harm, Schwarzschild 1975 は AGB 期シェルフラッシュが PNN 進化に及ぼす 影響を調べた。彼らはスタートモデルに 0.65 Mo と 1.0 Mo を選び、シェル フラッシュを抑えた計算で進化させた AGB 星に一度だけシェルフラッシュを 許し、その光度最高点をスタート点とした。彼らは外層からガスを剥ぎ取り、 0.63 Mo, 0.68 Mo とした。問題はこのような手続きで生じるシェルフラッ シュは正常なものよりずっと強くなることである。彼らの計算で PNN 経路 上で生じた1回のフラッシュは E-AGB 期に特有なトリプルフラッシュ型 であった。 |
Schomberner 1979, 1981, 1983 のモデル Schomberner 1979, 1981, 1983 は AGB から PNN にかけて全てのシェル フラッシュを丁寧に扱う計算を行った。彼のモデルは AGB 期にレイマース マスロスを受けて、MPNN/Mo = [0.55, 0.64] と比較的低質量であ る。計算を調節して、AGB 離脱時期をヘリウムシェルフラッシュ (1079), 間 フラッシュ期 (1981) と変えたが、かれはフラッシュサイクル位相の影響を系統 的に調べることはなかった。 Iben 1984 の研究 Iben 1984 は 0.6 Mo モデルについて、サイクル位相 φ = [0.7, 1.0] に対して、位相と進化の関係を詳細に調べた。この位相区間でのみ PNN 期間 内に最後のヘリウムシェルフラッシュが起きる。 この論文 ここでは、 Schonberner や Iben の計算を更に広いパラメタ―空間内で行う。 それらは (i) PNN 質量、(ii) AGB 離脱期位相 φ、(iii) マスロスの時間 変化、である。AGB - PN 進化に関しては Iben, Renzini 1983, Renzini 1984 を参照せよ。 |
|
PN 形成のマスロス率 PN 前駆天体=タイプ II OH/IR 星(Werner et al 1980, Zuckerman 1980, Jones et al 1983)、極端炭素星 (Knapp et al 1982) の観測から、PN マスロス が開始される時のマスロス率は 3 10-5 Mo/yr 程度である。この 割合で典型的な惑星状星雲質量 0.2 Mo に達するには 6000 年掛かる。そして、 この時間は、惑星状星雲の半径を膨張速度で割って得られる年齢にほぼ等しい。 一般にはシェルが電離し始めるのは 5000 年経ってからで、30,000 後には見 えなくなる。 速度加速 PN 形成の質量放出は PN シェル全体が係る、それ自体で独立な出来事であり、 星からの放出速度は低いが、何らかのメカニズムで次第に加速され、PNN がシ ェルを電離するほど熱くなる頃までには、PNe で典型的に見られるような膨張 速度に達すると思われる。 Sabbadin Hamzaoglu 1982, Robinson, Reay, Atherton 1982 は膨張速度が時間と共に増加する観測的証拠を示した。 スタートモデルの作成 MPNN = マスロスが実質的に終止した時の星質量。これは星が AGB にあった時よりもずっと小さい。ここでは MPNN = 0.60, 0.70, 0.76, 0.89 Mo を調べる。スタートモデルは Wood, Zaro (1981) での AGB 進化系列 M = 2.0 Mo, (X, Y, Z) = (0.68, 0.30, 0.02) から採った。 各スタートモデルは 12 回以上のシェルフラッシュを経験しており、本当の PN 前駆体とよく似た熱的緩和状態にある。Mc = 水素燃焼層内側の質量。 光度は全質量に関係なく Mc で決まる。有効温度 Teff は、外層質量 Me が極 端に小さい場合を除いて、全質量にはあまり依存しない。したがって、 PNN 与えられた MPNN と φ でスタートモデルを作るには、 (i) AGB モデル系列から Mc = MPNN, で与えられた φ のモデ ルを選ぶ。 (ii) 外層から質量を剥ぎ取り、外層を熱的に緩和させる。 剥ぎ取り量は、残った星が以前として AGB に留まり、残余水素量が PN マス ロスにより間フラッシュ期間内に消失する、ように決める。実験を繰り返した 結果、我々の初期マスロス 3 10-5 Mo/yr に対しては MeXe = 0.01 MPNN まで剥ぎ取るのが適当であることが分かった。 |
フラッシュ間期間 フラッシュ間期間は Mc で大体決まり、Mc 増加と共に急速に減少する。 例えば、Mc = 0.6, 0.7, 0.76, 0.89 Mo に対し、期間 = 68,500, 29,300, 16,600, 6000 年である。この長さは惑星状星雲シェルの放出時間 6000 年と 比較されるべきである。我々の選んだ MPNN 範囲の下限値付近では 我々のマスロス率では間フラッシュ期間のほんの一部の時間で全 PN シェルを 放出できる。上限値では、シェル放出時間と間フラッシュ時間が同程度となり、 定常星風がフラッシュサイクルの全位相を通して維持される。それにも拘らず、 AGB 進化はマスロスに影響されることなく進行し、Me ≤ 0.01 Mo になって AGB から離れる。与えられた MPNN に対し、星が AGB から離れる 時の位相が PNN のその後の進化を決定する。このために、前に述べた剥ぎ取り の時点での φ を指定する必要があったのである。 16種のスタートモデル 前に述べたように、我々は Mc が指定した4種の Mc の夫々に達した時の、 また4つの位相 φ = 0.0, 0.25, 0.50, 0.75 でのモデルを抽出した。 結局、全部で 16 のスタートモデルがある。夫々のモデルは 1 Mo/yr という 急速な剥ぎ取りを強制して、MeXe = 0.01 Mo にした。 マスロス継続期間の1 マスロス率は恒星の全体量 M, R, L で決まると考える。この場合 AGB 先端で 定常的な星風が吹き、星の全体量が AGB 先端とかけ離れるまで続く。このモデ ルでは、PNN が AGB を離れるまでマスロスには観測量を適用し、その後はゼロ に急落させる。 マスロス継続期間の2 マスロスは外層の元素組成で決まる。水素が残っている限りはマスロスが続き、 残余の水素が枯渇してマスロスが終了する。 |
|
マスロスタイプA PNN が AGB から離れる: log Teff = 3.8 まで、 dM/dt = 3 10-5 Mo/yr が継続。その後はゼロ。 マスロスタイプB 残余水素= 10-9 MPNN まで、dM/dt = 3 10-5 Mo/yr 継続。終了時の恒星表面物質は燃え終わった水素燃焼殻基部からの物質 である。この物質中の水素組成は 0.001 以下であり、表面物質はほぼ純粋な ヘリウムと言って良い。10-9 MPNN でマスロスを止め たのは主に計算上の理由であるが、その量の水素は実際上の影響は殆どない。 この場合の PNN はヘリウムリッチ PNN または DB 白色矮星として進化する。 |
観測可能性 注意しておくと、タイプAマスロスは星が AGB の上又は近くにいる時に起 こるが、タイプBの場合、マスロスのある部分は AGB 上かその近くで起き、 残りは PN 領域に入っても起きる。しかし、実際問題として PNN がここで 述べたマスロスを行っている現場を観測できる可能性は低い。タイプ A でも B でも、マスロス期間は短いからである。タイプ B で 0.01 Mo の水素をマス ロスで失う期間は 0.01/(3 10-5X) = 490 yr である。タイプ A ではさらに短い。その上、その時期の PNN は深いシェルに埋もれていて、 おそらく見ることは出来ないだろう。実際のマスロスはタイプ A と B との 中間であろう。 |
|
PNN 進化の一般的な様子 以前の PNN 進化計算の一般的な様子は良く知られている。AGB から離れる 初期進化は HR 図上を水平に移行し、その後衰退期に入って PNN から WD 領 域へ落ちて行くのである。この特徴は観測的に得られた Harman-Seaton 系列 (H-S 系列) と大体一致する。 |
PNN 期のヘリウムシェルフラッシュ 多くの場合、PNN は H-S 系列に沿って、水素またはヘリウムを、または交互 に、燃やしつつ静かに進化する。どちらになるかは AGB 離脱期にヘリウムフラ ッシュサイクルのどの位相にあるかに依存する。この殻燃焼は外層が薄くなり、 シェル温度がもはや燃焼温度に達しなくなったときに終止する。その後は、 収縮による重力エネルギーの放出が主なエネルギー源となる。しかし、 AGB 離脱期が次のヘリウムシェルフラッシュ直前であるような場合には、PNN 進化 の途中でヘリウムシェルフラッシュを起こす。Iben 1984 は 0.6 Mo モデルに ついて、この問題を注意深く調べた。この論文では様々なパラメタ―がどう影 響するかを調べた。 |

|
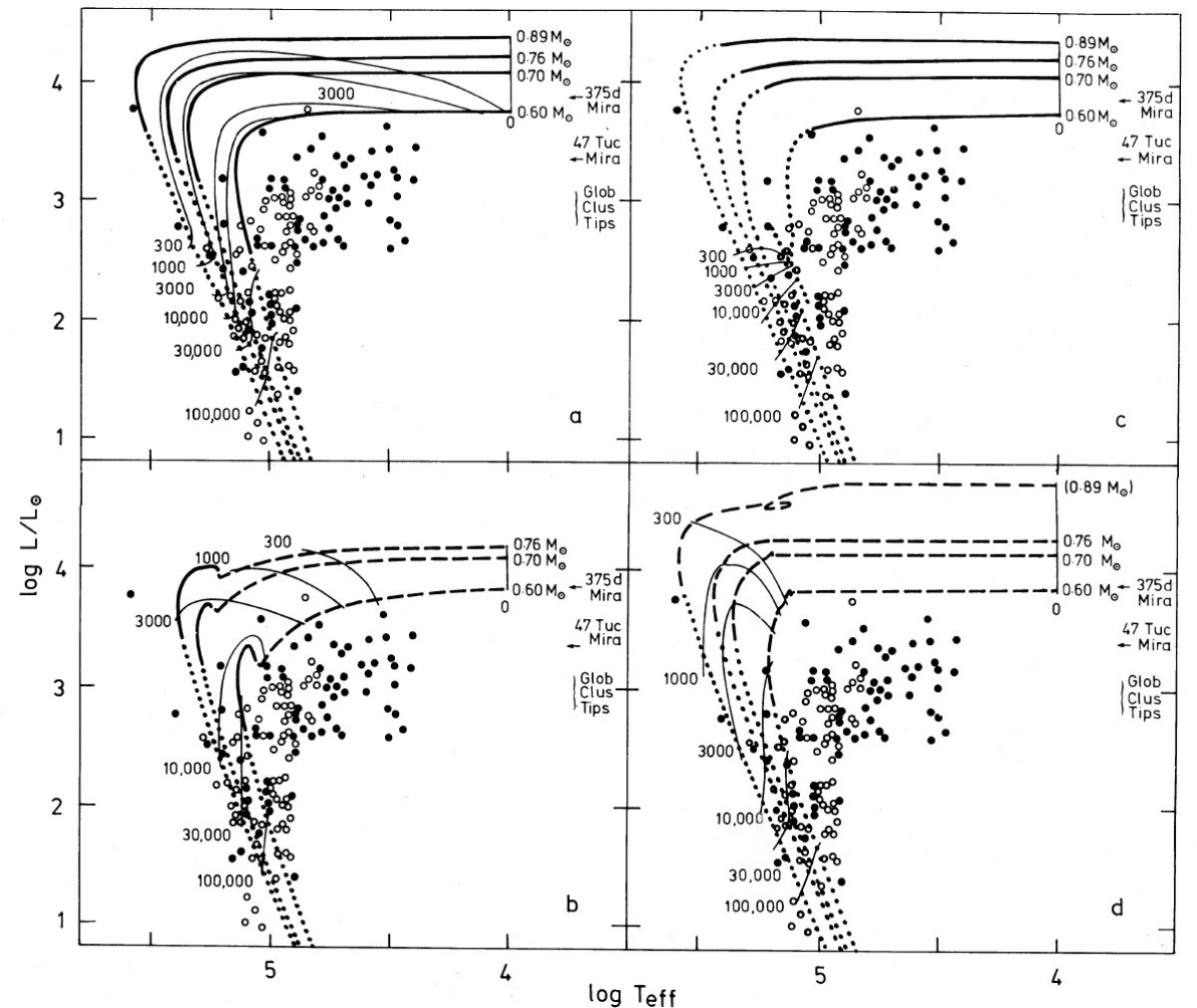
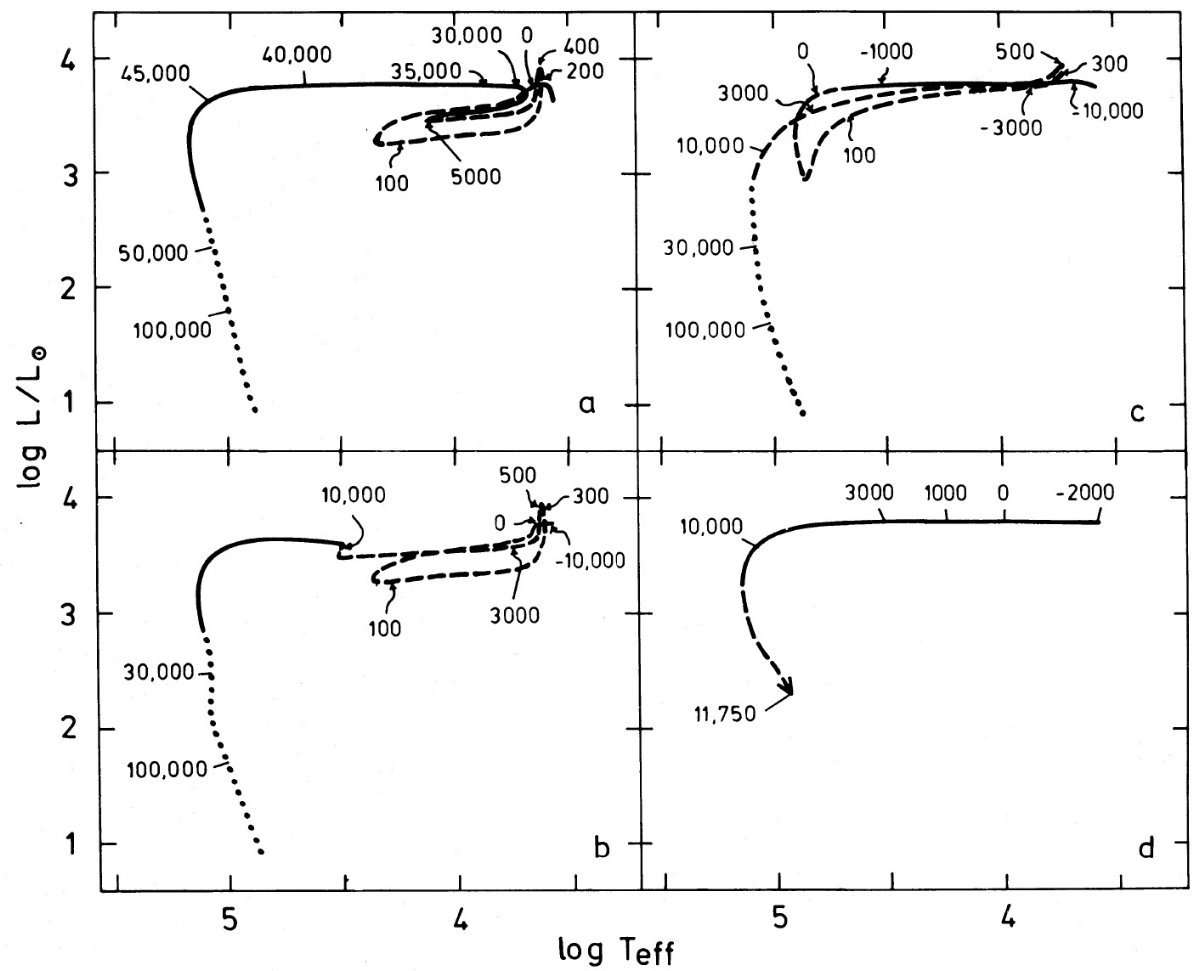
φ = 0.50 と 0.0 計算した 32 進化系列の結果は表1に示す。一例を除き、 φ = 0.25, 0.75 は φ = 0.50 と変わらない。従って φ = 0.50 と 0.0 を詳細に 検討する。それそれを間フラッシュ系列、フラッシュ系列と呼ぶ。例外となった のは M = 0.6 Mo,て φ = 0.75 で、最後のミクシングヘリウムフラッシュに 出合った。 0.89 Mo については、タイプ A, B どちらも、完全に収束するモデルを作れ なかった。理由は次節で述べる。それで、 14 系列を検討することになる。 それらの HR 図を図1に示す。図1、2から得られる特徴は、 1.全体の傾向 PNN 質量が大きいほど、より高温、高光度、高速の進化を示す。特に、PNN が Mv = 0 から 6 まで下がる時間は 低質量 PNN 程長くなる。 2.間フラッシュ系列でタイプ B 間フラッシュ系列でタイプ B の場合、 H-S 経路の水平枝の進化速度は 非常に速いので、 PNN 寿命のほぼ全てを Mv > 6 で過ごす。 3.タイプ A では タイプ A が log Teff = 3.8 で質量放出を止めることは 0.76, 0.89 Mo PNN 進化には影響しないが、低質量星では H-S 経路の水平枝寿命をかなり伸ばすこ ととなる。 |
4.フラッシュ系列は高光度期が長い フラッシュ系列では高光度期の寿命を延ばされる。 5.フラッシュ系列はタイプ A, B の差がない フラッシュ系列のタイムスケールは、間フラッシュ系列と較べると、タイプ A, B 間に差がない。 6.光度減衰の速度 光度減衰の初期は急速だが、 log L/Lo = 2.6 から速度が低下する。 7.M > 0.8 Mo 0.76, 0.80 Mo のどちらも L = 180 Lo になるまで 3000 年であった。この 一定性が M > 0.8 Mo 全部に適用できると、それらの検出率は等しくなる。 このチェックにはここでは使えなかった新しい計算テクニクが必要である。 タイプ B では水素発火が起きない 図1b に示す、タイプ A ヘリウム系列では、ヘリウム燃焼は水素燃焼にと って替わられる。その時に短期間の光度上昇が見られる。タイプ B ヘリウム 系列(図1d) ではマスロスの結果 PNN 期には水素量が不足するので 水素発火は起きない。例えば 0.6 Mo の場合、図1b では水素発火時に 5.5 10-4 Mo 水素量を保持しているが、図1d では水平枝の端までに 10-9 Mo になっている。 タイプ A での水素残量 タイプ A が水素燃焼を終えた時、まだ 10-5Mo - 10-4 Mo の水素が残っている。図1a, b で実線から点線への転換は水素燃焼が重力 エネルギー解放を下回った時期を表す。しかし、より低光度でも CN- チェイン から p-p チェインに替わって細々と燃え続けている。 |
|
基礎方程式 前に述べたように、ヘリウムフラッシュ系列の 0.89 Mo の計算は収束しな かった。これは外層対流層基部での輻射圧があまりに大きくなったためである。 静止モデルでは dPr/dP = (κLr)/(4πcGMr) (1) である。中心核付近で Mr = Mc, Lr = L として積分すると、 Pr/P = 1 - β = ⟨κ⟩L/4πcGMc (2) となる。β = Pg/P である。β は対流層基部で最小値を取る。 ヘリウムフラッシュの時何が? ヘリウムフラッシュで光度パルスが生じたとする。式 (2) の L がエディン トン限界 Led = 4πcGMc/⟨κ⟩ を超えた時何が起きるだろうか? この問題を探るため、Mc = 0.89 Mo に対し、様々な M, L の外層積分を行った。 計算手順は以下の通り (i) (L, M, Teff) のセットを選ぶ。 (ii) 静水平衡の式を表面から内側に積分する。 (iii) 対流層の基部で圧力が急上昇する。 (iv) 対流層の底の質量がコアマスである。 (v) 正しい Mc が得られる Teff を探す。 外層積分の結果 こうして得た結果を M = 0.9, 2 Mo に対して図3に示す。2 Mo は PN 前駆 AGB 天体の典型例、0.9 Mo は AGB 離脱に近い例である。光度は M = 0.89 Mo の AGB 星がヘリウムフラッシュサイクルで経験する幅を選んである。0.9 Mo と 2 Mo の双方で、βmin は式 2 で評価した値に非常に近い。 二つのモデルでの β の差は低質量モデルでは κ が大きいことに よる。L が Led に近づくと対流が深くなり、ついに対流層がヘリウム燃焼の 想定位置 r = 0.01 Ro を突き抜けるようになる。これは、現実の星では ダイナミカルな膨張が始まる時期に当たり、それは静力学平衡解が存在しない 事に現れるのではないか。 |
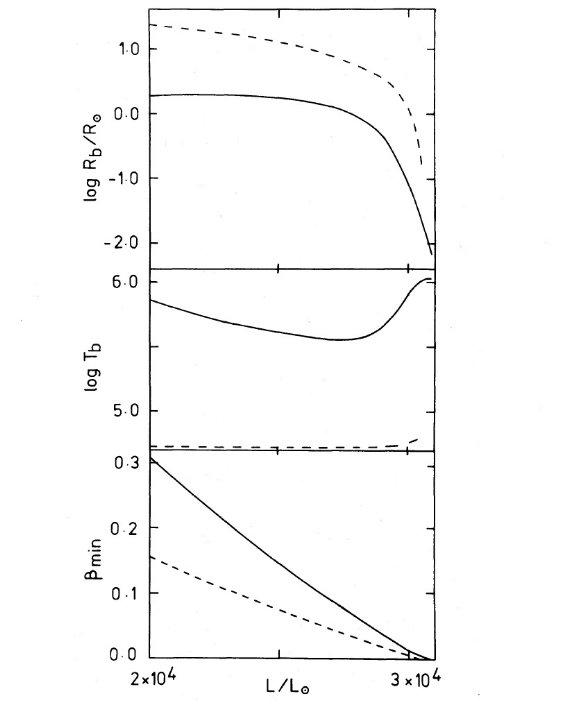 図3.βmin = β の最小値、Tb = 対流層底 での温度、Rb = 対流層底半径と 0.89 Mo PNN 光度の関係。 実線=総質量 2 Mo, 破線=総質量 0.9 Mo. |
|
収束不能の意味 0.9 Mo モデルの βmin は 2 Mo モデルより小さい。これは 低質量モデルでは κ が大きいからである。外層質量が減るにつれて、 対流層基部の密度が薄くなり、オパシティが大きくなることは、 AGB 星が 対流層基部で Led に近づいた時に質量減少によりそこでの Led が下がり、 L > Led になる可能性がある。その時には完全な外層放出が起きる。 我々の 0.89 Mo モデルで起きたのはそれではないか。2 Mo モデルはそのような 分解は起こらないが、計算の収束は困難となる。このため Mc > 0.89 Mo の PNN 進化計算は出来なかった。 計算不安定 同様の計算不安定は Rose, Smith 1972 も 0.9 Mo コアに外層を付ける計算 で経験している。しかし、より大きい Mc に対して不安定性の報告はない。 これは M > 3 Mo の計算だかららしい。図4を見ると分かるが、外層質量が 大きくなると、不安定を起こすのに必要な L も増加するからである。 エネルギー Paczynski 1969 が既に述べているが、外層の総エネルギー=熱+電離+重力 は正である。重力エネルギーを考えてみよう。Mc = 0.89 Mo モデルでは、 外層質量の大部分は 600 Ro に位置する。ここから 1 Mo 質量を無限遠まで 移す絵エネルギーは 6.4 1045 erg である。 Wood, Zaro (1981) のヘリウムフラッシュ光度から 1.7 1047 erg が シェルから外層に移される。その時表面光度変化は 10 % 以下である。従って、 フラッシュエネルギーの 4 % で 1 Mo 外層を無限遠に持っていける。 脈動不安定 多くの研究によると、脈動不安定の方が輻射圧不安定より先に起きる。 従って、静止平衡光度限界が達成される以前に大質量放出が起き、所謂 超星風がこれらの脈動により発生する。我々のこの静止平衡不安定は 光度に上限を設定するものであろう。 |
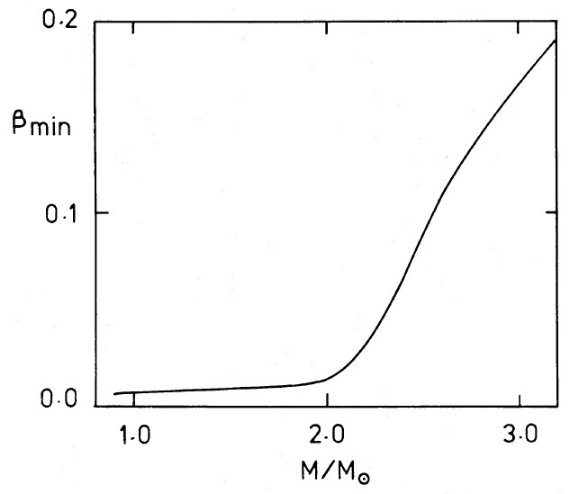 図4.Mc = 0.89 Mo, L = 3 104 Lo の時、βmin と M の関係. |
|
ヘリウムフラッシュの4つの例 φ = 0.75 で AGB を離脱した 0.6 Mo タイプ A PNN 系列は F-S 経路の 光度衰退期でヘリウムフラッシュを起こしている。低いマスロス率を適用した テスト計算では 0.6 Mo PNN の幾つかで水平枝上でのヘリウムフラッシュも起 きていた。図5にはヘリウムフラッシュが起きたケースを AGB からの距離 準に並べた。表2にはそれらのデータを示す。水素量はマスロスで外層質量 がどのくらい減少していたかの目安になる。 ケース (a) (a) は殆ど AGB 上にある時に起きた。その結果二回の大きなループが生じる。 どちらも AGB に復帰する。似た現象が Schonberner 1983, Iben 1984 で報告 されている。 ケース (b) ケース (b) は (a) より少し起きているが、ほんの少し の追加マスロスの結果は大きな差を生み出した。今回は AGB への復帰は起き ない。そして、水素燃焼が PNN 領域では最低温部 log Teff = 4.5 で回復し た。 ケース (c) ケース (c) ではフラッシュ以前に星雲の電離が開始される。それにも 拘わらず AGB 極近くへの復帰が起こった。ただ前者と違うのは第2ループが 見られないことである。実際水素燃焼は起きず、ヘリウムフラッシュ後直ちに 重力収縮に入る。 ループは観測可能か? 最後のフラッシュが水平枝上で起きた場合、第1ループは数百年で起き、 ヘリウム燃焼のエネルギーが表面まで達する前に終了している。 |
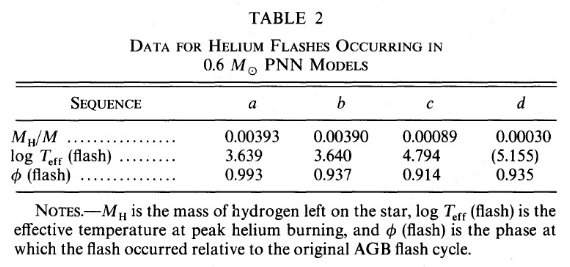 表2.0.6 Mo PNN モデルのデータ |
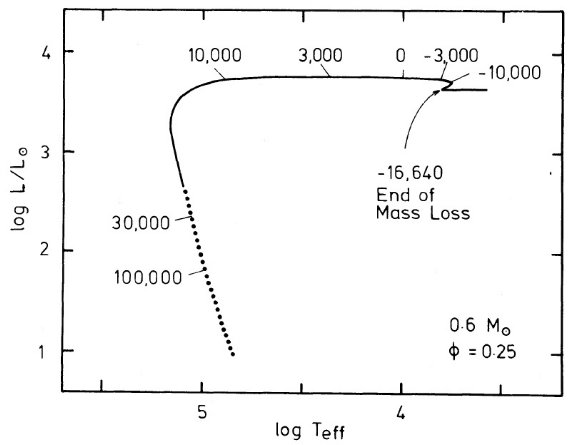 図6.0.6 Mo PNN 進化。φ = 0.25 で AGB 離脱。 AGB から PN 領域までの経過時間は ttr = (MeR - MeN)/(dM/dt) で与えられる。MeR = 主マスロス期終了時の外層質量、 MeN = Teff が 3 万度を超えた時の外層質量。dM/dt = 殻燃焼と マスロスの結果外層質量が減る速度。MeN はモデル計算でよく決 まっているので (dM/dt) と MeR の不定性が問題になる。 フラッシュによる AGB への復帰 ttr の一般論は Iben, Renzini 1083 に詳しい。ここでは MeR の不定性を調べる。AGB マスロスは log Teff = 3.7 - 3.8 になったら停止すると仮定されている。 MeR はこの時点で決定さ れるしかし、与えられた Mc に対し、MeR は L に依存する。 (?) L を大きくすると、星は AGB に近づく。これが post-AGB フラッシュを受けた星が AGB に復帰する理由である。 図6= φ = 0.25 タイプA進化 さて、ヘリウムフラッ シュ後の光度低下期に超星風が停止したとしよう。その後表面光度は間フラッ シュ光度極大に向けて増大して行き、 AGB へ復帰する傾向を見せる。その結果 AGB から PNN への時間が延長される。この様子は図6にはっきりと示されて いる。そこでは、φ = 0.25 で AGB を去った 0.6 Mo PNN がタイプ A で、 log Teff = 3.8 でマスロス停止する進化経路が示されている。シェルフラッ シュサイクルの早期には光度増加率が最大であるので、 ttr の遅延 は最大となる。表1に載せた 0.6 Mo タイプ A の遷移時間 ttr にはこの効果が良く現れている。それは高質量になると呆けてくる。注意すべき は、0.6 Mo のように小質量 PNN では、この早期位相での AGB 離脱による静謐 水素燃焼期が引き起こす AGB から PN への遷移の遅れは PN シェル膨張時間の かなりの部分を占めることである。例えば、φ = 0.25 の 0.6 Mo モデルで は, ttr = 2 104 年である。こうして、もし超星風停止 が起きる位相が均等であるなら、上に述べた遅延効果は、PN半径と PNN 位置 との間に元来存在したであろう相関を覆い隠してしまう。 |
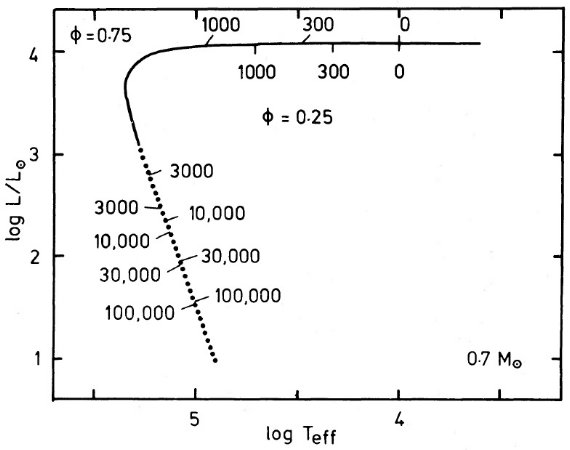 図7.0.7 Mo PNNi φ = 0.25, 0.75 AGB 離脱の進化。二つの経路は時間 スケール以外では区別できない。経路の下又は右にマークした時間は φ = 0.25 のもの。 ( タイプAかな?) 図7=位相と進化速度の関係 タイムスケールへの第2の影響は、 HR 図上の PNN 領域内での進化に及ぼす 放出期の位相である。図7には、φ = 0.25 と 0.75 の経路を描いた。二つ は殆ど重なって区別できないが、時間だけが違う。一般には φ が早いと PNN 進化速度が遅い。 Schonberner 1981, Iben 1984 と比較 我々の計算を Schonberner 1981, Iben 1984 と比較する。0.6 Mo PNN で 間フラッシュ期に AGB 離脱した場合、log Teff = 4.0 からの水平枝期間は Schonberner 7000 年、我々が 12000 年、 Iben が 18000 年である。光度 低下期で較べると、log Teff = 4.0 から測り、 30000 年後に Schonberner は log L/Lo = 1.9, 我々は 2.3, Iben は 1.8 まで低下している。 0.6 Mo AGB 離脱がシェルフラッシュ時に起きた場合のタイムスケールに関 しては、 Iben 1984 と我々の結果の間に大きな差がある。例えば、我々の モデルでは、水素燃焼ピーク光度に達するのは log Teff = 4.0 を通過後 18000 年経ってからだが、Iben 1984 のモデルでは 60000 年掛かる。 この差は主にフラッシュ間隔 Δt が Iben 1982 と我々のモデルで大きく異なるためである。Iben では log Δt = 5.4 に対し我々は log Δt = 4.8 と大きく異なる。2倍分はモデル組成差 で説明できる。フラッシュ間隔が長くなると、水素燃焼再点火までの時間も伸びる。 |
|
Pottasch 1983, Kaler 1983 のサンプル 図1には Pottasch 1983, Kaler 1983 の PNNi サーベイの結果を示す。Kaler 半径 0.175 pc 以上の大きな星雲に重点を置いている。一方 Pottasch は Shklovsky 法による距離決定で使われる標準質量のような「天体物理学」仮定 にできる限り依存せずに HR-図をサンプルを集める方針を取った。彼は 距離と温度を決める幾つかの方法を使用した。このため天体の選択基準は非常に 入り組んだものとなった。 サンプルは暗すぎる 図1を見ると、特に Pottasch のサンプルは、PPNi の質量は 0.6 Mo 以下と 結論しそうである。しかし、このサンプルは他の観測と食い違いがある。特に AGB から離れる時の光度が球状星団巨星枝先端光度より低いのは問題である。 また、 LMC で典型的な P = 375 d ミラよりは更に暗い。Pottasch サンプルの 光度は実際の3倍暗いのではないか。 |
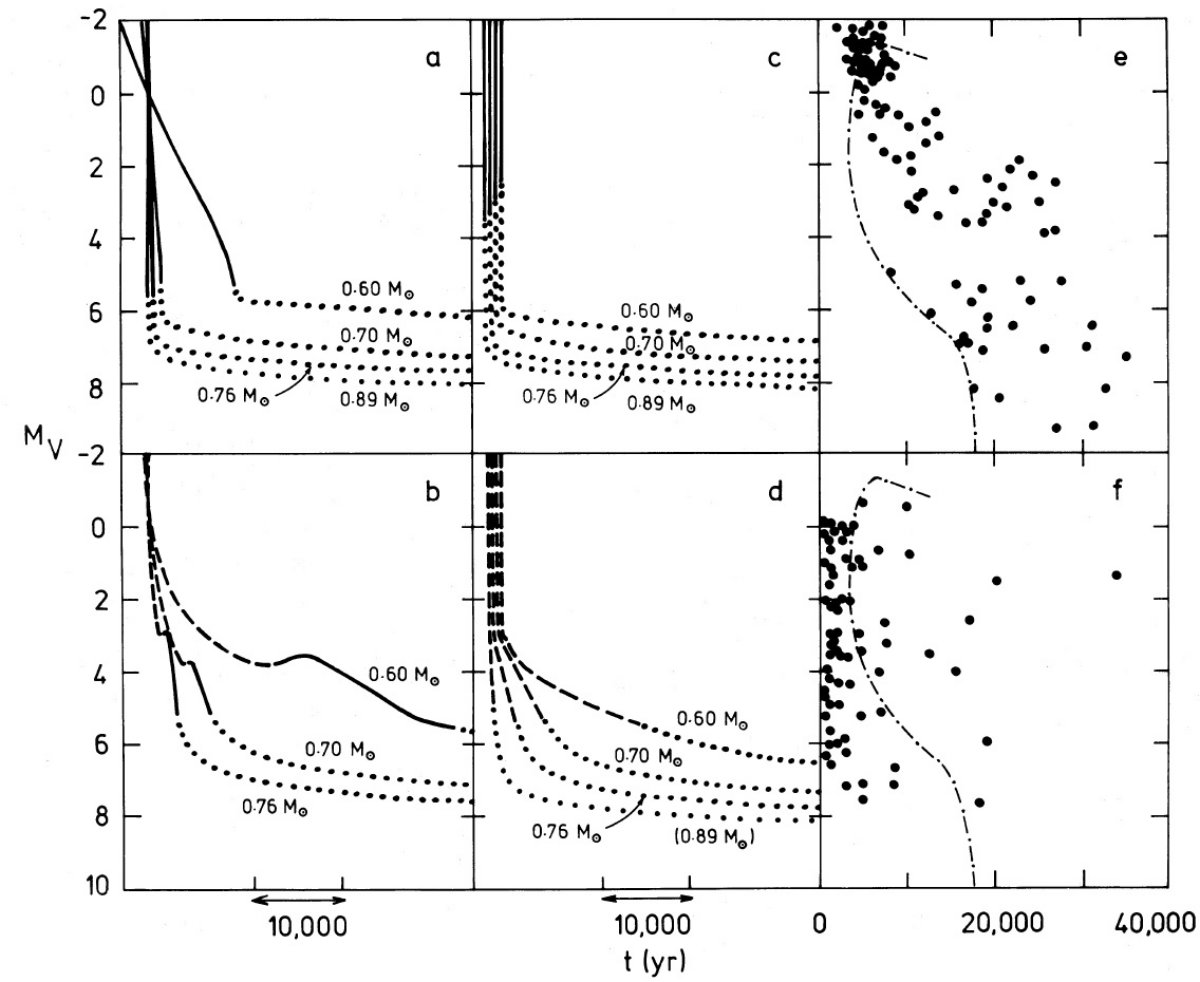
Schonberner 1981 の時系列 もう一つの方法は、モデル時間系列を観測のシェル半径の膨張年齢と較べる ことで、図2に示した。これは Abell 1966 が最初に行った方法である。 図2e には Schonberner 1981 の観測資料を示す。彼の図7を参照せよ。 彼自身はこの図を、唯一本の進化系列の存在を示すものと考えた。彼の 経路を図2の (Mv,t) 上の一点鎖線で示す。比較のために図2f には Pottasch のサンプルを示す。2e と 2f の相違は、観測とモデルの比較から結論を導く ことに疑いを投げかける。 略す その他、DA, DB 白色矮星、C 再結合によるマスロスなの度の話を略す。 |
|
臨界コアマス M < 3 Mo の AGB 星に対して臨界コアマス 0.86 Mo が見つかった。それ より上ではシェルフラッシュの時に水素外層は輻射圧で吹き飛ばされる。AGB 星質量が 3 Mo より大きい場合は、その運命は超星風の効率次第である。 もしもコアマスがチャンドラセカール質量に達する前に星風の結果星質量が 3 Mo 以下になったなら、輻射圧による外層放出メカニズムが働く。そうでない 時には超新星となる。 この輻射圧メカニズムは少なくともある種の DB 白色矮星とヘリウム PNNi nの形成に関与している。また、マゼラン雲で明るい AGB 星が少ないことの 説明にも関係する。 離脱位相の効果 間フラッシュ期に AGB を去った星では、 AGB から PNe までの時間はフラッシュ サイクルのどの位相で離脱が起きたかに強く影響される。サイクルの早期=間 フラッシュ光度極小からの回復期、に離脱した星は電離光を発するまでに非常 に長い期間を水平枝状で過ごす。例えば、 φ = 0.25 で離脱した 0.6 Mo PPN は Teff = 30,000 K になるまでに 20,000 年掛かる。 |
冷却期 0.8 Mo より大きいと冷却期の光度低下が速くなると以前は信じられていた。 しかし、低下速度は大きく変わらない。従って、以前の想定より多くの高質量 中心核が見つかるはずである。 観測との比較 我々の進化経路と H-S 系列を較べると、最近報告された PNN 光度はファク ター3暗いと思われる。観測データの更なる見当が必要である。 |