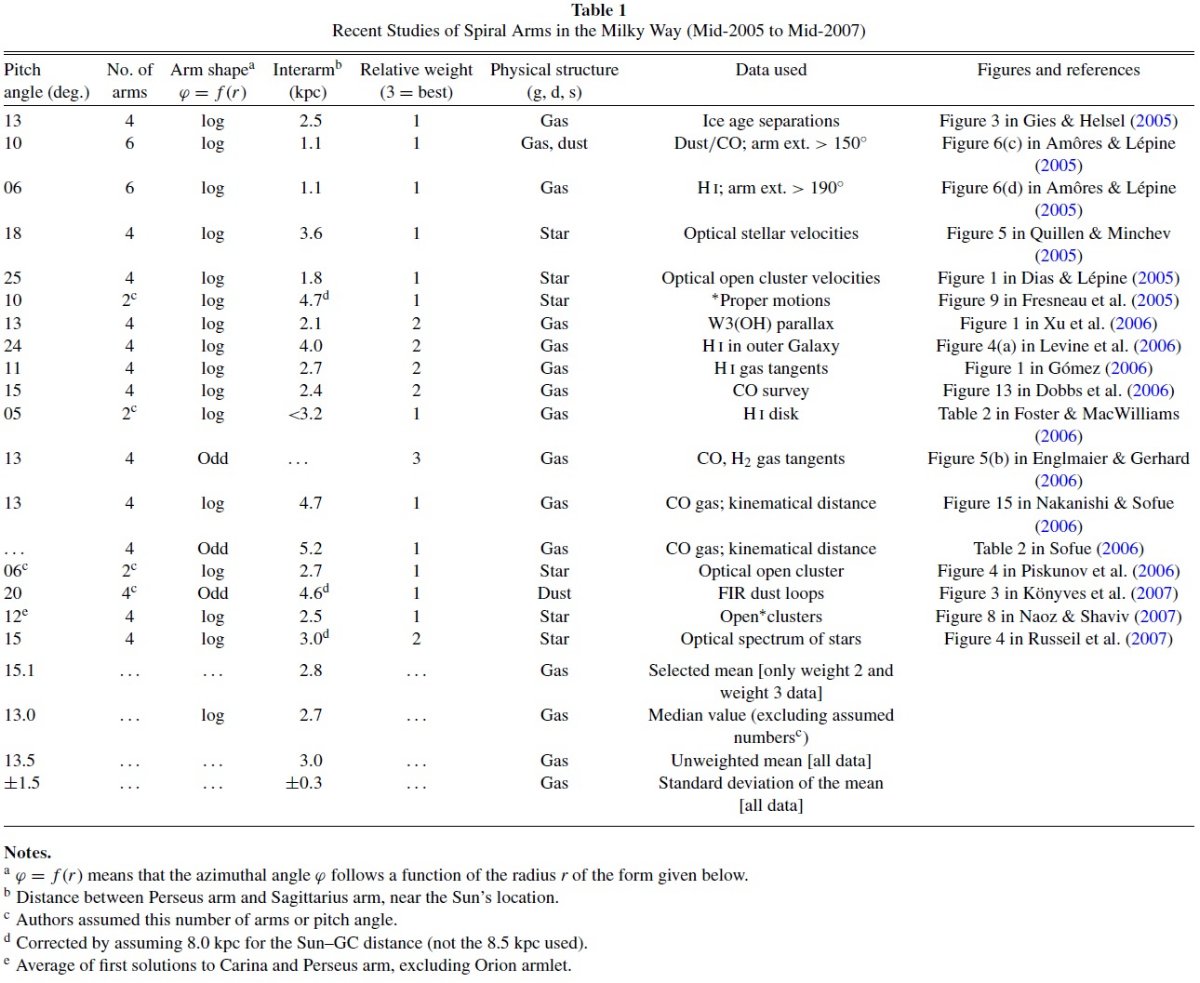
| 渦状腕の位置(ピッチ角、形、数、腕同士の間隔)と速度(回転 曲線)に関する最近の成果を評価し、以前の数値と較べる。それに基づいて データ平均値にフィットする、地理学的モデルを作成した。銀河系四分区 内の腕の断片の一つづつに対して LSR 視線速度を計算した。我々の 速度距離モデルから、視線の腕交差点が速度空間で予想される。 | モデル予想と CO 観測データとの比較を銀河系四分区で行ったが、結果は 良好であった。我々の方法は単純であるが、観測との比較が容易である。 この速度距離決定法は銀河系地理学と共生関係にあり、互いに矛盾しない。 ペルセウスとシグナス腕の混合を例示した。また、 4 kpc 付近での 4本の渦状腕出発点の銀経・速度混合も論じる。 |
|
これまでの腕モデル研究のまとめは以下のようである。 1980-1994 Vallee et al 1995 1995-2001 Vallee et al 2002 2001-2005 Vallee et al 2005 | この論文では、これまでに発表された位置モデルを用いて腕の固有速度マップ を予想する。その逆ではない。運動マップは良い腕の位置マップは与えない。 |

|
評価 公表されたデータを評価して、重み1,2,3を付ける。ダストの影響を 受けているデータは、不規則なダスト分布の補正が不完全になるので低い評価 を受ける。円軌道を仮定して得た距離も既知の非円運動を考慮すると低い 評価になる。視差や接線のように仮定が少ない距離決定法は大きな重みを与える。 局所腕は本物か? 局所腕のような光学構造は物理的に本物の腕ではないかも知れない。 または実在するにしても Piskunov et al. 2006 が言うような減光スクリーンのような影響で見え方が本当とは大分異なって いるかも知れない。 重み3のデータ Englmaier, Gerhard 2006 質量モデルを用いて CO と HI の終端速度曲線と腕接線データをフィットした。 彼らはモデルに対数螺旋を強制していない。 重み2のデータ Xu et al 2006 W3(OH) l = 134 のメタノール 12 GHz メーザーの視差 = 1.95 kpc を導き、 長い間議論のあった距離の問題に決着を付けた。その視線速度中間値 = -43 km/s はこの天体をペルセウス腕の向こう側に置く。一方、シグナス 腕はこの方向で -60 km/s である。 Gomez 2006 間違った速度モデルを使うといかに銀河系の像がゆがむかをモデルによって 示した。彼は二本腕ポテンシャルからの対応として4本ガス腕を導いた。 Levine et al 2006br> HI の表面密度分布を導いた。円軌道にエピサイクル運動が加わった モデルを使用し、各腕は独立している。マップ上で各腕は銀経により 巾が変化する。 Dobbs et al 2006 平滑化粒子流体力学モデルを CO 観測とフィットした。大きな分子雲は 渦状腕内部に含まれることを見出した。彼らのモデルは円軌道に限定されて いない。 Russeil et al 2007 可視域分光と U, B, V 測光から、23 個の HIIR 距離を改定した。 そして、シグナス腕における速度偏差を見出し、 ペルセウス腕における偏差を確認した。 重み1のデータ Gies, Helsel 2005 氷河時代は太陽が渦状腕を通過している間の現象であると 考えて、過去 500 Myr の4回の通過を決めた。で可視星の 速度をフィットし、局所渦状腕を得た。 Amores, Lepine 2005 ダストとガスが良く混じり合っているという星間減光モデルを HI, H2/CO サーベイと較べた。彼らは 14 - 18 の 渦状腕断片をフィットした。 |
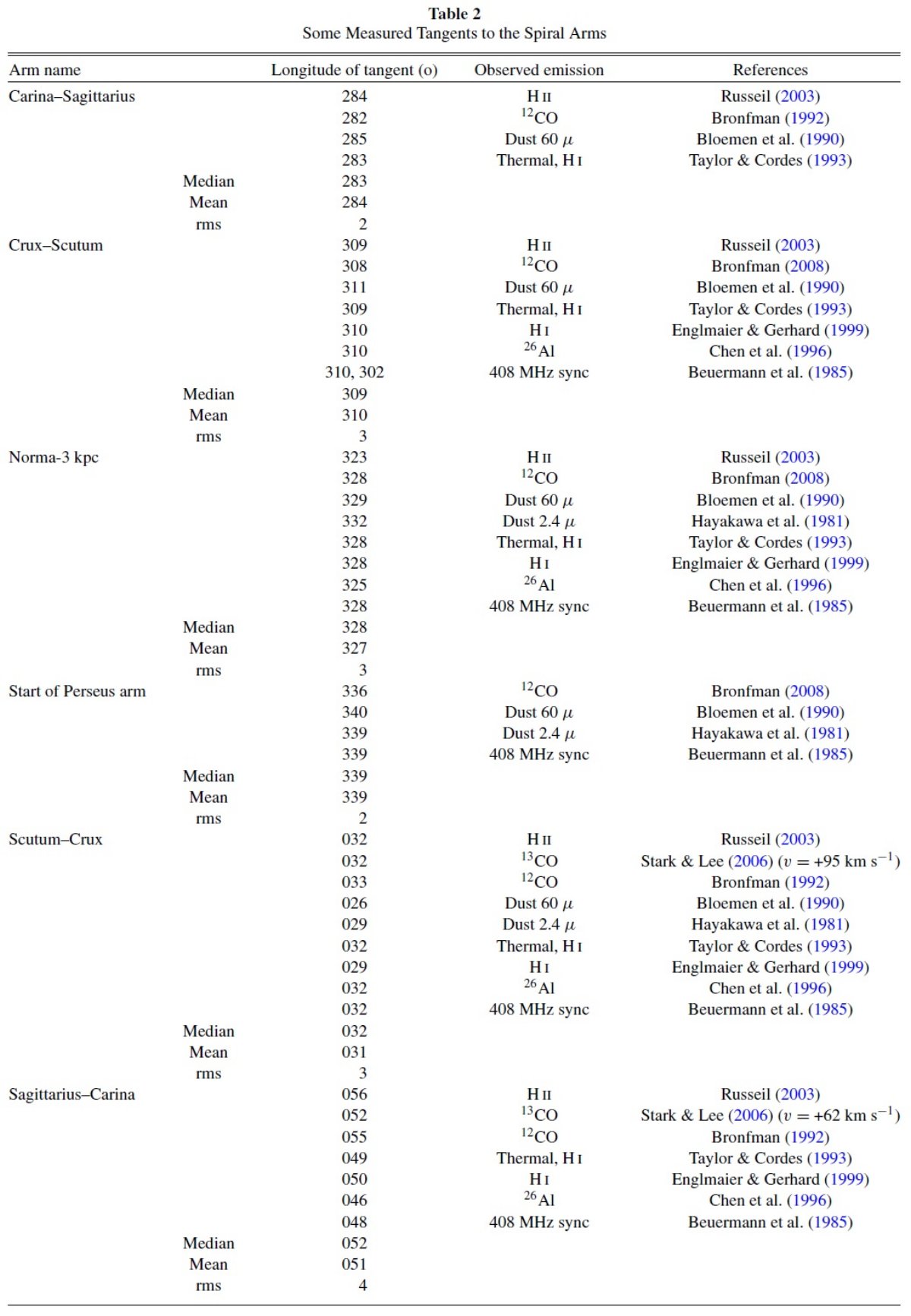
Guillen, Minchev 2005 可視星の運動がエピサイクルであると仮定したモデルDias, Lepine 2005 散開星団の星が生まれた場所を用いて渦状腕の位置を決めた。しかし 多くの腕間星団が見られ、腕位置の決定は困難であった。 Fresneau et al 2005 l = [310, 315] にある可視で明るい星の固有運動を求めた。それらの距離は 0.5 kpc 以内に限られる。彼らは星がサジタリウス腕に沿って流れていると 仮定した。 Foster, MacWilliams 2006 HI データに二本腕密度波のある円回転モデルを適用して二本腕 のピッチ角を決めた。 Nakanishi, Sofue 2006 CO データから3Dガスマップを作った。 Sofue 2006 CO と HI の視線速度勾配を用いて、太陽・銀河中心線近くの腕距離を 決めた。彼は非円運動を全て無視した。 Piskunov et al 2006 可視星団を渦状腕にフィットしようと試みた。かれらは二本腕に フィットさせるためピッチ角を 6° という低い値にした。 Konyves et al 2007 IRAS 60, 100 μm マップから遠赤外ダストループを探した。それらが 腕をなぞっていることを見出した。次に彼らはループ内部にそれらの 距離が既知の前駆天体を探した。 Naoz, Shaviv 2007 可視散開星団の生まれた場所を決定し、「multiple spiral sets = 多重腕セット」の証拠を見出した。例えば、サジタリウス・カリーナ 腕は二つのセットが重なり合っている。一つはパターン速度 30 km/s/kpc ピッチ角 21 で、もう一つは 16 km/s/kpc でピッチ角 15 である。 彼らは腕巾を 0.7 kpc と仮定し、パターンスピードに特異速度の 補正は行わない基本回転運動のみを仮定した。 表1=2005-2007 の結果 表1には 2005 - 2007 の渦状腕に関する結果を載せた。Ro = 8 kpc の補正以外は文献通りの値が使われている。例えば減光補正に ダストのマダラ性を考慮しないと天体を系統的に遠くに見積もる。 また、固有運動補正を正しく行わないと距離を近くに見積もる。運動 と距離の関係でショックによる速度のジャンプを考えないと、 遠すぎたり、近すぎたりする。従って、全ての平均を取るのが 自然である。 表2=接線方向の観測の結果 表2には接線方向の観測の結果をまとめた。分子雲、ダストレーン、若い星 で接線方向は少し異なる可能性がある。銀河中心から 3 kpc、又は銀経 22 以下 l = [338, 22] ではバーが存在し、渦状雲の星と力学的に分離が困難である。 Englmaier, Gerhard 1999 は 腕接線データを収集した。ただし、彼らはカリーナ腕 l = -76 を完全に無視 した。また腕の名前はその後次のように変化した。 ケンタウルス腕は十字座腕に。 3 kpc 腕はペルセウス腕のスタート点に。 その後の新しいデータの幾つかは彼らの集めたものよりも感度、分解能の点で 優れている。また 13CO のようにその後現れた新しいタイプの データもある。 |
|
Ro Eisenhauer et al (2005) の 7.6 kpc をこの論文では採用する。表1 は Ro = 8 kpc を使用した値が 載っているが、訂正は行わない。 バー 最近の研究はバーが複合的であることを示唆している。しかし、我々はバー 構造は扱わず、最終結果に上書きするのみである。 3.1.新しいモデルフィット平均法の理由づけ色々な新しい方法の結果を平均すれば渦状腕の真の姿にかなり近いという 仮定を表1で採用した。採用した論文が数個、重み2と3、であるのは、系統 誤差が入り込む可能性のある方法を除いたからである。色々な手法の平均をとる ことで、プラスに働いたり、マイナスに働いたりする較正エラーの影響を軽く したと考える。 研究の基本方針 腕のピッチ角、腕の数、腕の形、Ro を入力として用いて、以前の天の川銀河 地図作製学モデルを改訂できる。モデルフィットからは8つの出力を正しく導 く必要がある。それらは、6つの接線方向(表2)、腕間隔=ペルセウス腕とサジタリ ウス腕の太陽位置での間隔(表1)、W3(OH)間での距離 = 1.95 kpc である。 我々は基本データの平均値を入力として、腕の正確な位置を求めるという方針を 採っている。したがって、銀河面上に散らばった個々の天体をつなぐという方法は 使わない。この論文では完全な対称性を仮定しているが、完全に対称な腕構造 を示す銀河が実際には僅かであることは確かである。しかし、この論文は腕構造 のスタートであり、将来の研究が偏差を明らかにしていくだろう。 W3(OH) の意義 Xu et al 2006 の決めた W3(OH) l = 134 の距離は重要である。ペルセウス腕 には W3, W4, W5 が数度に亘って伸びている。W3(OH) はその中に含まれ、 ペルセウス腕の中央部から近い可能性が強い。 入力パラメタ― 入力は4つで、p = 12.8°, m = 4, 対数螺旋、Ro = 7.6 kpc である。 これらは過去の論文 I, II, III と表1での値を考慮した。それらは、 ⟨p⟩ = 11.6, 11.7, 11.1, 12.6, 13.5, Ro = 8.0, 7.2, 7.9, 7.6 である。 θ0 と r0 の決定 対数螺旋の表示は以下の式で与えられる。 tan p (θ - θ0) = ln (r/r0) θ0 と r0 を変えて、表2の6個の接線方向と W3(OH) 位置が合うようにする。その結果、 θ0 = -20±5 と r0 = 2.1 ±0.1 を得た。この新しいパラメタ―から出る結果は (i) 腕間距離 = 2.76 kpc (ii) W3(OH) までの距離 = 1.97 kpc (iii) 6個の接線方向 |
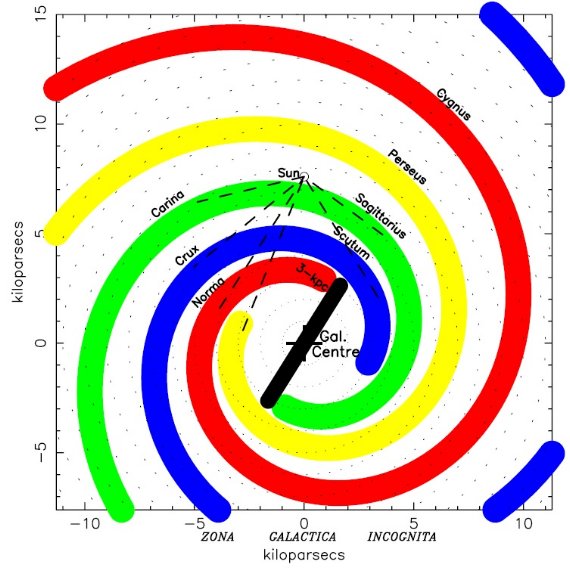 図1.我々の運動学的モデルと合う、地図作製法によるベスト解。破線= ガス、ダスト、星の観測から決めた実際の腕の接線。青い腕切片が十字ー盾座 腕の外挿上にあることに注意せよ。 腕の名前 図1にはこうして得た地図作製学的モデルを示す。破線は観測から決めた接線 である。青色腕は第1象限では盾座腕(Scutum arm)、第4象限では南十字座腕 (Crux arm)と名前を変える。この腕の先端部は第1象限銀河中心の向こう側で 再び現れ、さらに第2象限にもその続きが見られる。赤色腕もやはり名前を変え、 内側銀河系では 3 kpc 腕、定規座腕(Norma arm)であるが、外側銀河系では 白鳥座腕(Cygnus arm)と変わる。同様に、サジタリウス腕(Sagittarius arm) はカリーナ腕(Carina arm)となる。ペルセウス腕(Perseus arm) でさえ内側銀 河系では分子リングの一成分として混同される。 白鳥座腕の呼び方 最近ペルセウス腕の外側の腕は様々な呼ばれ方をされていて、例えば、 白鳥座腕(Cygnus arm)、ペルセウス+I腕(Perseus+I arm)、 定規座-白鳥座腕(Norma-Cygnus arm)など。我々は白鳥座腕を好む。 太陽近傍の腕 太陽近傍 1 kpc の局所的な腕片を、初期の論文ではオリオン腕、オリオン -白鳥座腕、白鳥座腕、シグナス領域(Cygnus region) と呼んだ。我々はこの 太陽付近の小さく局所的な星の集まりをオリオン腕片と呼ぶ。 |
|
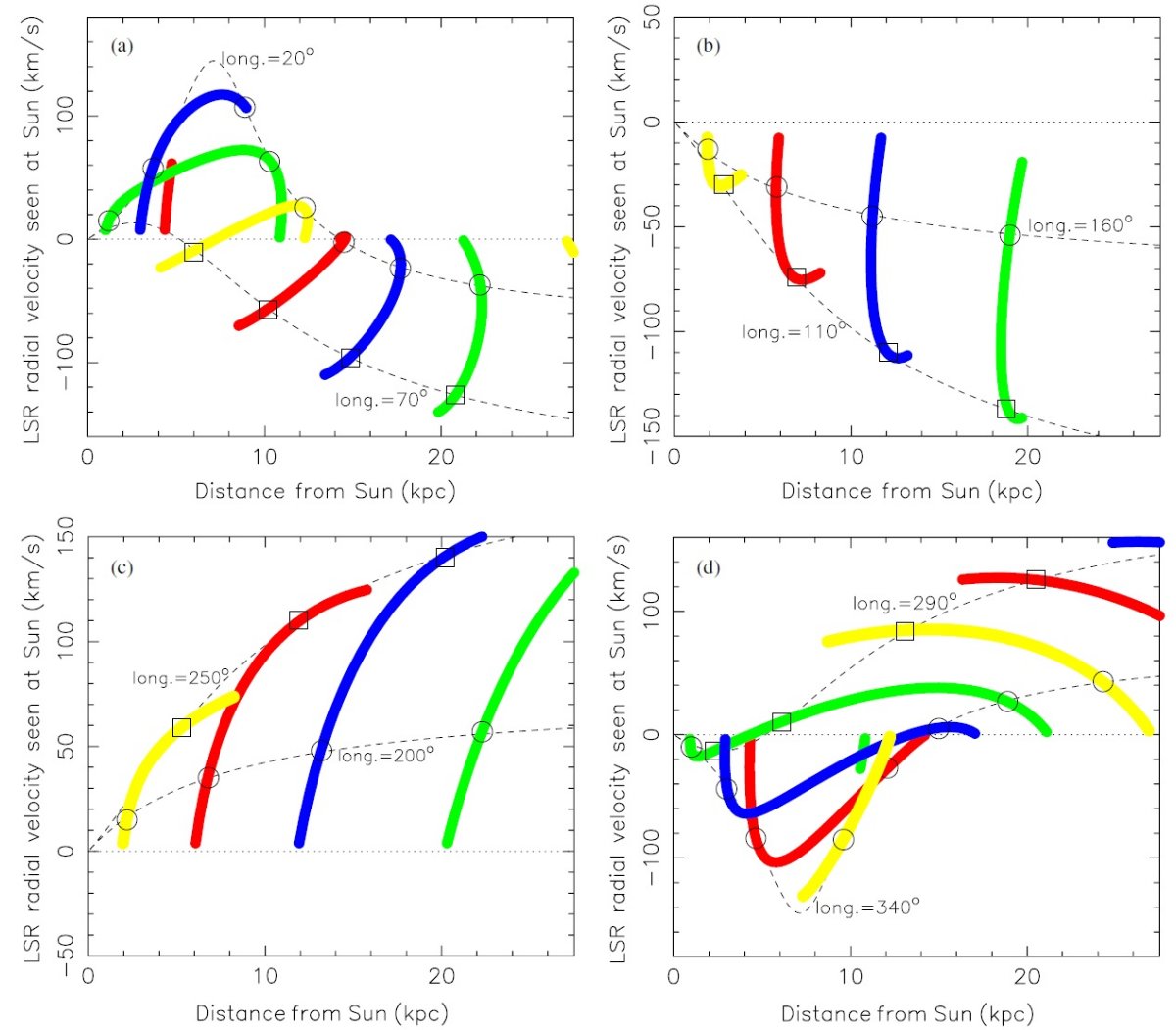
腕の発生領域 R = 3 - 5 kpc の領域では4本の腕が発生し、その間に間隙が生じている。 以前の角分解能の低い観測ではこれを分子リングと呼んでいた。例えば、 Brown et al 2007 の図1、Taylor, Cordes 1993 の図3、 Dame et al. 2001 の図3.4つの渦状腕の発生部分を低分解能で眺めるとリング状に見えるので ある。所謂 4 kpc 分子リングは連続した物理構造ではなく、装置の低分解能 によるものなのである。その根拠を示すと、 (i) l = 340 付近にペルセウス腕の発生領域がある。図2(d)にその距離の 範囲が広いこと、図3(d) には視線速度の範囲が広いことが示されている。 (ii) l = 33 付近は盾座腕の発生領域が見かけ上の分子リングと重なっている。 図1」参照。 |
(iii) l = [-15, 15] の分子リングは他の二つの腕、サジタリウス腕と定規
座腕の発生源に起因している可能性がある。図1を見よ。これらは
Sawada et al. 2004
が発見した銀河系中心分子バーとの重なり合いの上に現れるだろう。 その他に、Englmaier, Gerhard 1999 は分子リングは渦状腕の組が二つ から成っていると主張した。この説は 中西、祖父江 2006 も賛成している。 5 kpc リング l = [21, 30] VLSR = [40, 120] km/s には 13CO 観測 Jackson et al 2006 図3に "5 kpc ring" のようなものが見える。 しかし、実際にはそれは我々の南十字・盾座腕と一致する。彼らもそれはリング ではないかも知れないと述べている。 |
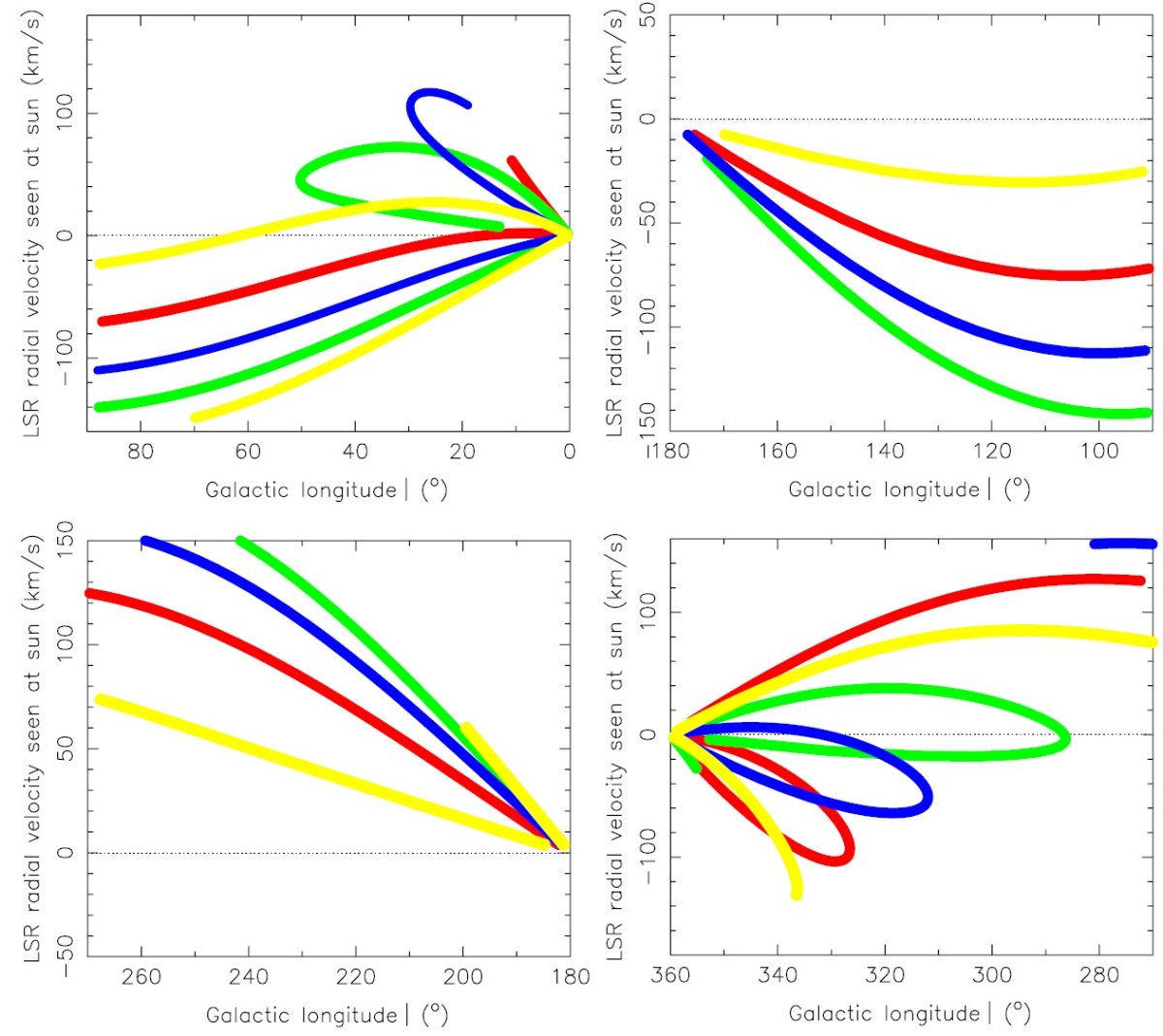
4.1.新しい予言個々の天体にモデルをフィットしない渦状腕のモデルと標準速度曲線を合わせると、腕の速度モデルを作れる。 内側銀河系ではバーの存在が非円運動を引き起こす。しかしこの論文では バーの外側の銀河回転を扱う。図1のような腕のマップを変換して銀緯- 速度関係に直すことが出来る。我々は個々の天体に我々のモデルをフィット しない。 Vo 最近の太陽位置での回転速度の研究は 220 km/s 付近に収束している。 4.2.距離・速度マップ第4象限図2は各腕の太陽からの距離・視線速度マップを示す。妥当性テストと して、l = 340 の視線速度、図2(d), は HI 観測に基づく Kothes, Dougherty (2007) 図1とそっくりである。さらに、彼らの論文の図3にあるように、 l = 340 の HI プロファイルは渦状腕に対応する全てのピークを示す。 特に V = -140 km/s の最高速ガスは予想通りである。 彼らは V = [-140, -100] km/s のピークはガス密度の超過によるものではなく、 同じ速度の成分が積み重なった所為、つまり広い距離範囲に渡る同じ速 度を有するガスからの放射、であることを見出した。 4.3.図3 = (l, v) 図図3には各腕の (l, v) 図を示す 。前にも述べたが、CO データは半乱雑な 分布を示す。そのよい例は、Jackson et al 2006 図3の l = [18, 36], v = [0, 120] km/s の半乱雑分布、 Dame et al. (2001) 図3の同じ銀経でのやはり半乱雑な分布である。このように CO が何処にでも ある状況では4つの腕が何処にあるかを (l, v) 上に探すのは大変困難である。 第1象限では、我々は図3の腕予想位置を観測された分子雲位置と較べることが できる。 |
|

|
|
|

|
|
|

|
|
|

|
|
|

|
|
|

|
|
|

|
|
|

|
|
|

|
|
|

|
|
|
