Optical Properties of the Silicate Dust Grains in the Envelopes around AGB Stars

　アブストラクト　

　１．イントロダクション　

　２．ダストオパシティ　

　２．１．オパシティ関数　

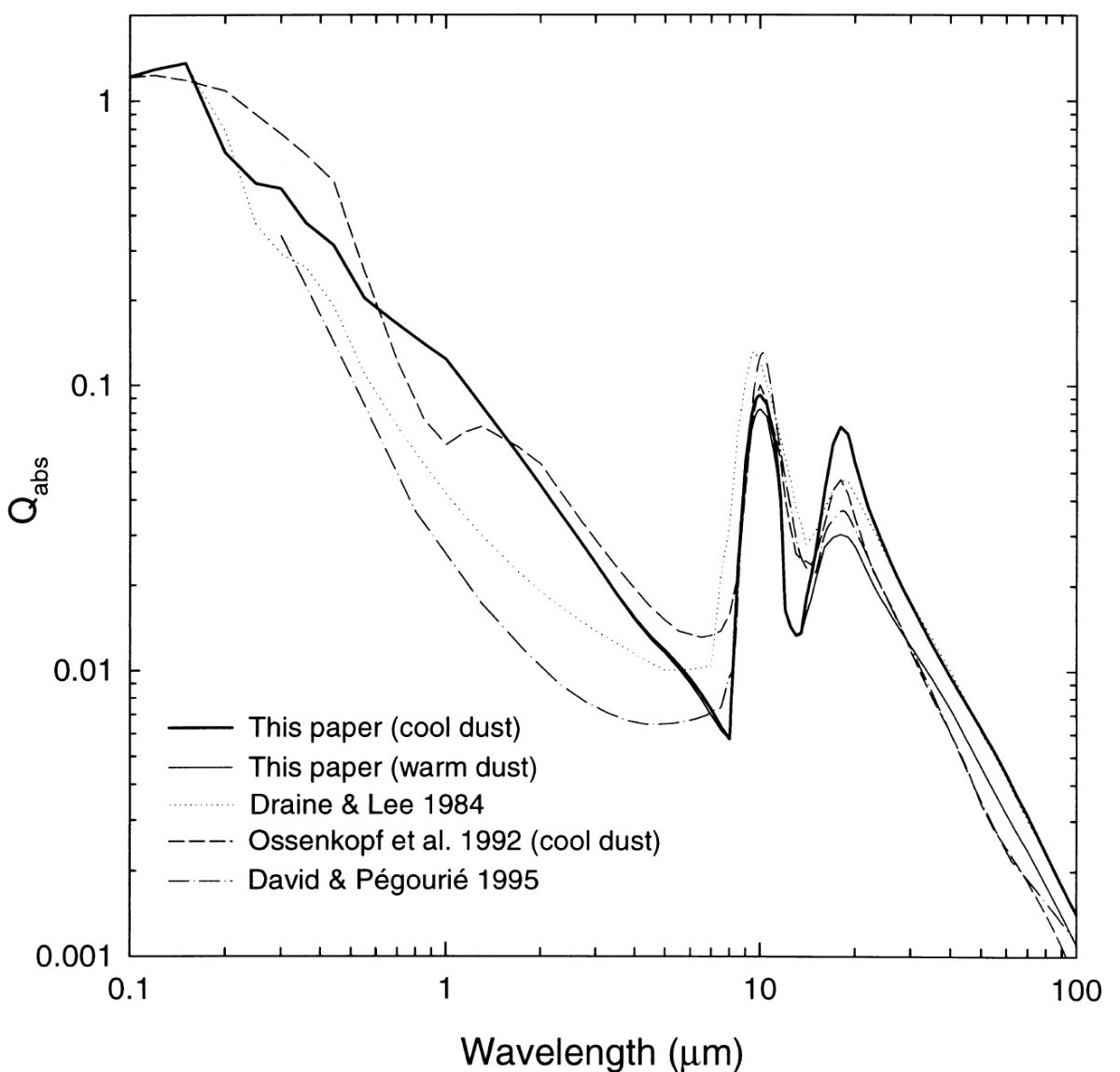
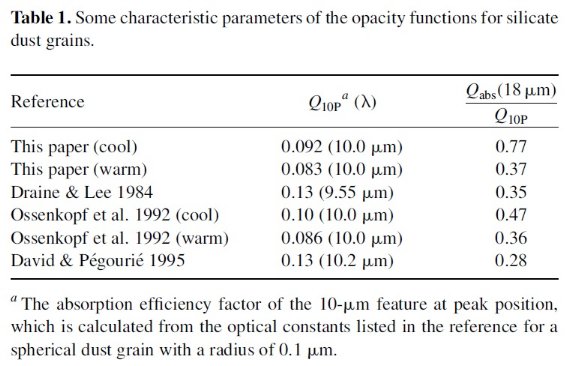表１．オパシティ関数の特性 　暖かいダストと冷たいダスト　 　図１には今回求めたダスト吸収効率を以前の研究値と比較した。 ここに示した Q は 半径 0.1 μm の球形グレインに対するものである。 今回、暖かいダストのオパシティは 10 μm 放射帯を示す OH/IR 星との フィットから、冷たいダストのオパシティは 10 μm 吸収帯を示す OH/IR 星とのフィットから求めた。二つは λ < 8 μm では同じ である。しかし、 λ > 13 μm では、冷たいダストの 10, 18 μm ピーク値及び、全体の値も大きくなる。表１には様々なオパシティ モデルの特性をまとめた。 　レイリージーンズ近似　 　この論文では半径 0.1 μm を仮定する。サイズパラメター 　　　x = 2πa/λ << 1　 の時には、

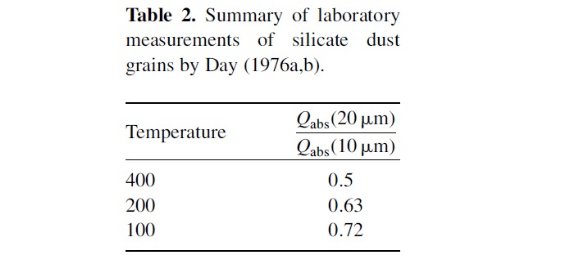表２．Day 1976 が測定したシリケイトグレインの特性 Ｑがレイリージーンズ近似 　　　Qabs = Qext = (8πa/λ) Im[(ε-1)/(ε+2) からあまり離れない。従って、 a < 0.5 μm のダストで、λ > 1 μm ならば、半径にはこだわらない。 　オパシティの温度依存性　 　Bedjin 1987, Volk, Kwok 1988, Suh 1991 が述べているように、観測に フィットするダストオパシティは、光学的に厚いシェルに対しては λ > 13 μm で大きい値を取る。これは、オパシティに温度 依存性があることを意味する。Day 1976 は減光効率が温度依存することを 実験で見出した。表２にその結果をまとめた。簡単に言うと、 200 K 以下に 冷やすと、Qext(λ>13μm) が上昇し、一方 Qext(λ=10μm) は一定値である。 Jones, Merrill (1976) は T < 250 K または < 125 K で吸収を生む出すためには大きな Qext(λ=10μm) が必要と述べている。Pegourie, Papoular 1985 はダストの成分、サイズ分布が場所により変わる必要があると述べた。 しかし、彼らが議論するダストサイズの変化は非現実的である。

　２．２．光学定数の導出　

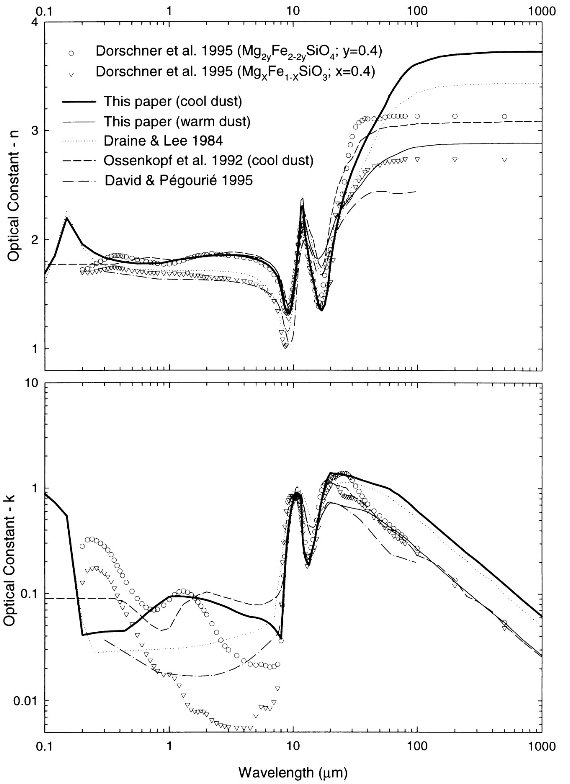図２．シリケイトダストの光学定数。

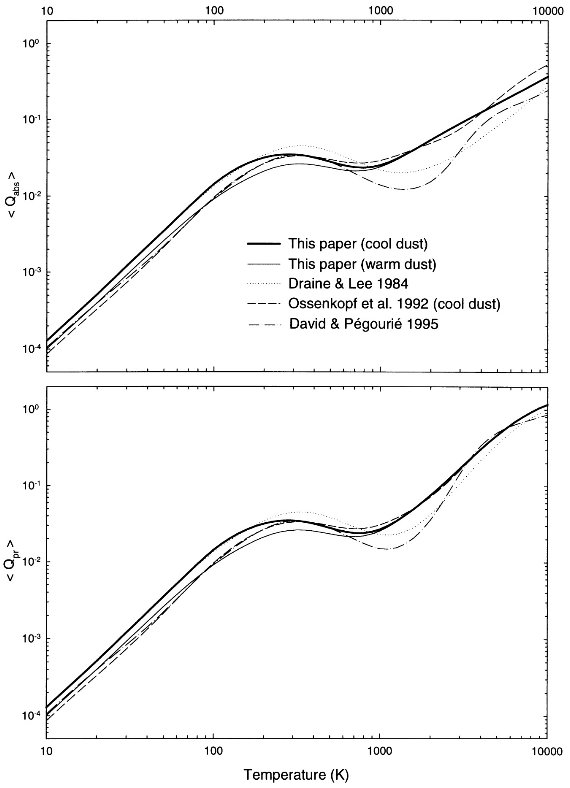図３．プランク平均輻射効率 と温度 T の関係。

　３．ダストエンベロープモデル　

　３．３．ダスト密度分布

色々な提案　 　通常の研究では密度分布には　r-2 則を仮定する。 r-3 則や r-1 則の方がフィットが良いという主張も あるが、輻射圧モデル (Kwok 1975, 小笹ら 1984) や、脈動と衝撃波を 加えたモデル (Bowen 1988, Suh,Jones,Bowen 1990) は r-2 則 に近い。　 　マスロス増加の影響　 　AGB 進化を考えるとマスロス率は時間と共に増加する。従って、全体としては 質量分布は逆二乗より急なはずである。ダスト凝結半径 Rc は普通の OH/IR 星で、Rc ∼ 3 1014 cm である。 Vexp = 10 - 20 km/s とする とこれは 6 年程度に相当する。図４には, マスロス率が連続的に増加する 場合の密度分布を示す。 R < 1000 Rc まではマスロス率変化に伴う 密度勾配のズレは無視できる。超星風現象を扱う際にはこの限りではなく、 もっと複雑な分布則 Suh, Jones 1997, Suh 1997 が必要となる。 しかし、ここでは R-2 則を仮定する。

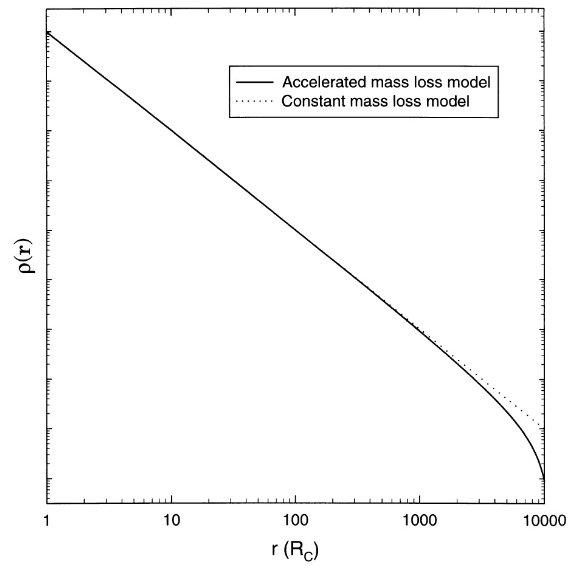図４．加速マスロスと定常マスロスの二つでの密度分布

　３．４．ダスト温度とオパシティ　

暖かいオパシティと冷たいオパシティ　 　図５には(上)＝ダスト数密度分布と(下）＝ダスト温度分布を τ 10 = 0.01 と 10 の場合について示す。 この論文では暖かいシリケイトと冷たいシリケイトの二種類のオパシティ を別々に用いた。10 μm 放射帯を持つ星には暖かいシリケイトオパシティ、 吸収帯の星には冷たいシリケイトオパシティを使用してモデルフィットを 行った。放射帯から吸収帯への変換は τ10 = 3 付近で起こる。 　マスロス率　 　シリケイトの巨視密度＝ 3 g cm-3, Rc = 3 1014 cm, Vexp = 15 km/s, ダスト/ガス = 0.01 を仮定して、マスロス率は、 3 10-8 Mo/yr (τ10=0.01), 9 10-5 Mo/yr (τ10=50) である。 ( dM/dt = Ng(Rc)Rc^2、τ＝Ng(Rc)κ∫(Rc/R)^(2)dR= κNg(Rc)Rc=κ(dM/dt)/Rc つまり、dM/dt = τRc/κ である。κ(cool)/κ(warm) = 1.1 (図１)、 [dM/dt(cool)]/[dM/dt(warm)] = 3000, τ(cool)/τ(warm)=5000 を入れると、 3000 = 5000 [Rc(cool)/Rc(warm)]/1.1 Rc(cool)/Rc(warm) = 0.66 になる。マスロスが大きくなると Rc は増加する センスではなかったか？ )

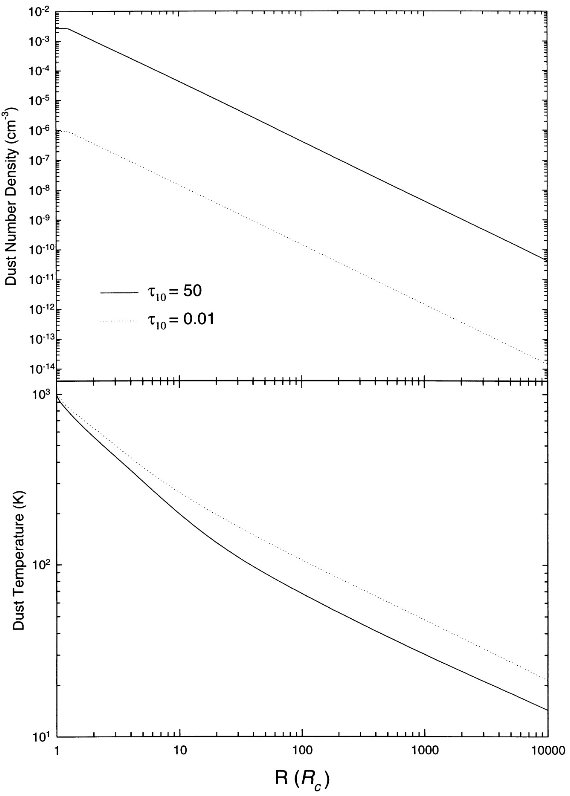図５．ダスト数密度 Ng とダスト温度の距離による変化。R はダスト凝結半径 Rc からの動径距離。 (とあるが、 R は中心距離を Rc 単位で表示した量でないか？ )

　４．ＳＥＤの比較　

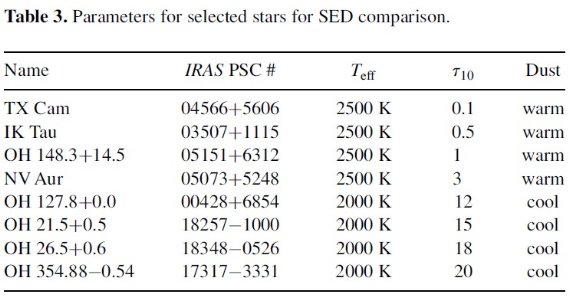表３．モデルフィットのパラメタ― 　観測データ　 　比較に用いた赤外データの大部分は Fourth Catalog of IR Observations (Gezari, Pitts,Schmitz 1998) から採った。幾つかの場合では、 異なる時期に得られた SED を他の時期のデータと合わせるためにスケール を調節した。 　天体　 　光学的深さを広い範囲で代表するように８個の OH/IR 星を選んだ。 表３にそれらに対するモデルパラメタ―を示す。モデルフィットの結果 を図６−９に示す。どのモデルでも暖かいオパシティと冷たいオパシティ のフィット結果を示した。 　二種のオパシティ　 (i)　光学的に薄いダストシェル。 　　　　TX Cam 　　　　IK Tau 　　　　OH 148.3+14.5 暖かいオパシティが良く合う。 (ii) 中間型 　　　　NV Aur 　　　τ10 = 3 くらい。どちらも同じ程度のフィット。 (iii) 光学的に厚いシェル 　　　　OH 127.8+0.0 　　　　OH 21.5+0.5 　　　　OH 26.5+0.6 　　　　OH 354.88-0.54 　　　暖かいオパシティでは光学的深さをどんなに厚くしても 18 μm 吸収帯は作れない。

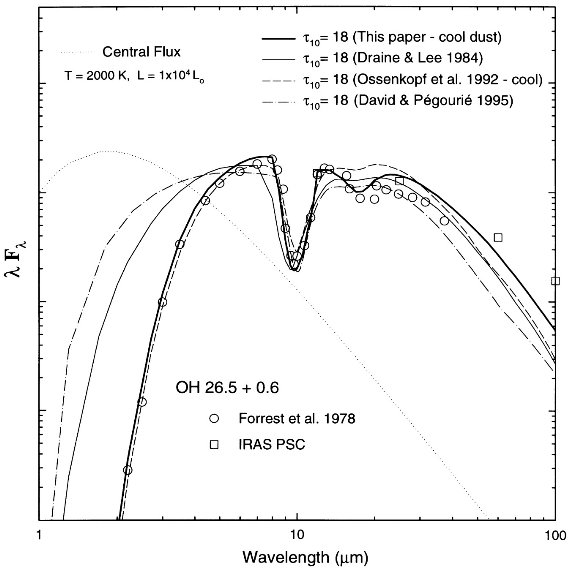図１０． OH 26.6*0.6 を様々なオパシティでフィットした。 　OH 26.5+0.6 を用いた比較　 　図１０では OH 26.5+0.6 を様々なオパシティでフィットした。 ρ ∝ r-2, Tc = 1000 K を仮定してフィットしたモデル 　SED を較べた。この仮定では今回のオパシティが最良であったが、 元論文では異なる密度、温度の仮定でフィットしていることを注意する。 (i) 図１で分かるように、10 μm 吸収帯オパシティは互いに似ているので、 そこのフィットはどれも良い。 (ii) Ossenkopf et al 1992 は λ < 13 μm で良いフィットだが、 18 μm 吸収を生み出せない。 (iii) Ossenkopf et al 1992 の基論文では、 Tc = 1500 K を仮定。 (iv) David, Pegourie 1995 は Rc/Rs ∝ Ts3 仮定。 (v) 現在、 Draine, Lee 1984, Ossenkopf et al 1992, David, Pegourie 1995 が良く用いられている。より適切なオパシティモデルを観測との 対比を同じ条件で較べて選ぶべきである。

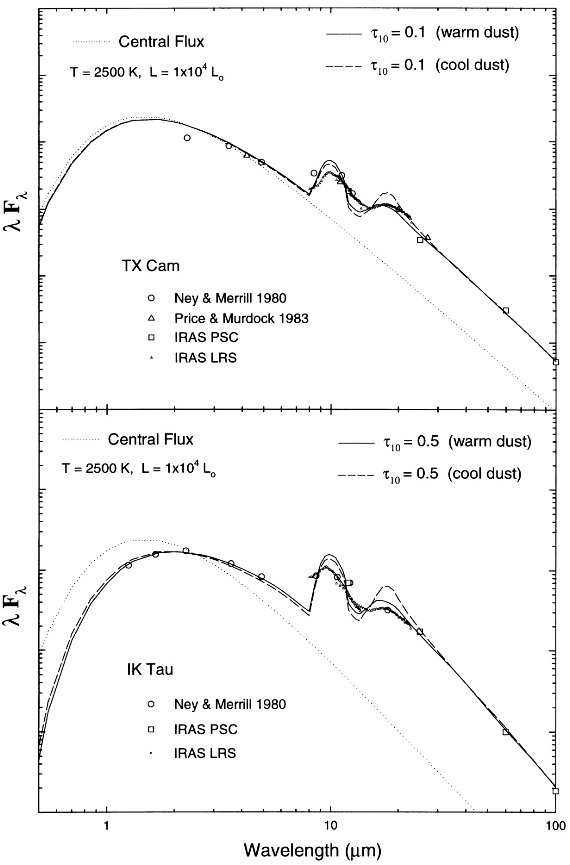図６．上＝TX Cam。下＝IK Tau。

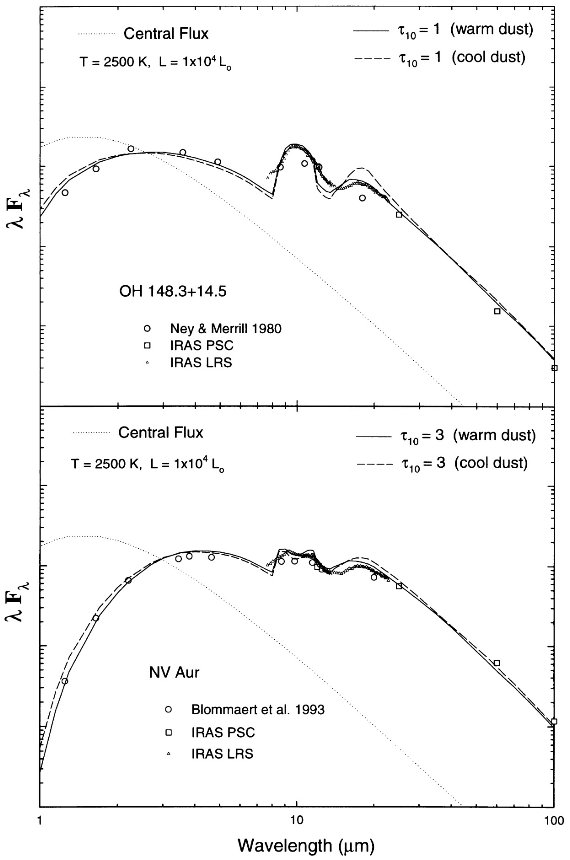図７．上＝OH 148.3+14.5。下＝NV Aur。

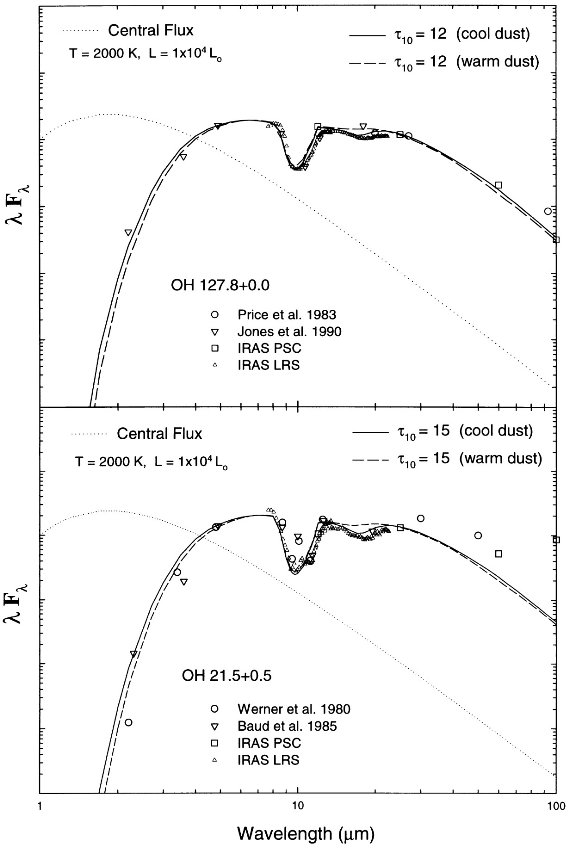図８．上＝ OH 127.8+0.0。下＝ OH 21.5+0.5。

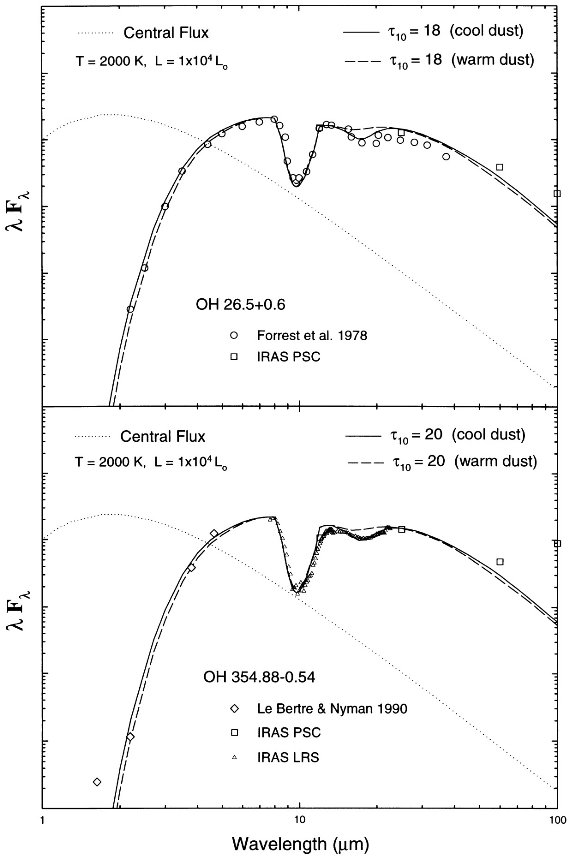図９．上＝ OH 26.5+0.6。下＝ OH 354.88-0.54。

　５．二色図　

不完全なデータ　 　完全な SED データを持つ OH/IR 星は少ない。その多くは IRAS フラックス が分かっている。また多数の OH/IR 星には NIR - 10 μm バンドまでの 測光データがある。SED には不完全なデータでも二色図には使える。 　K-L 対 A(10)　 　Jones, Gehrz 1990 と Lawrence, Jones, Gehrez 1990 は K-L カラー と 10 μm 吸収帯強度 A(10) との関係を二色図として調べた。 A(10) の定義は Lawrence, Jones, Gehrez 1990 に載っている。 彼らはダストシェルモデルが観測された傾向に良く合っていることを 見出した。 　モデルとの比較　 　図１１のデータは Lawrence, Jones, Gehrez 1990 に幾つか強い メーザー源を足したものである。モデルは τ10 = 0.01, 0.05, 0.1, 0.5, 3, 7, 15, 30, 40 をつないだ。今回のモデルは、 τ10 ≤ 3 では暖かいオパシティ、τ10 > 3 では冷たいオパシティを使用した。シェルなしの星は通常の 赤色巨星 K-L = 0.2, A(10) = 0.0 に位置する。

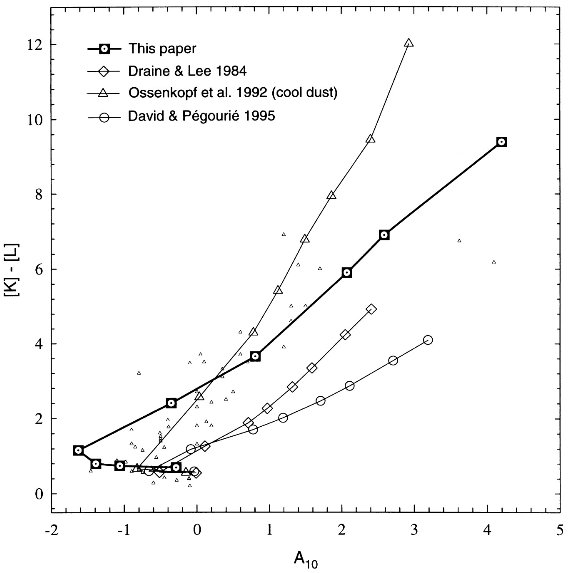図１１．(K-L) と A(10) との関係。

IRAS が見た OH/IR 星　 　IRAS PSC には OH/IR 星とされた星が 1597 星ある。それらは、 Lewis, Eder. Tezian 1990 Le Squeren et al 1992 David, Le Sequeren, Sivagnanam 1993 Blommaert, van der Veen, Habing 1993 Chengalur et al 1993 Loup et al 1993 Xiong, Chen, Gao 1994 Lepine, Ortiz, Epchtein 1995 Lewis 1997 Kwokm Volk, Bidelman 1997 van Loon et al 1998 である。図１２には 870 OH/IR 星をプロットした。ラインは τ10 = 0.01, 0.05, 0.1, 0.5, 3, 7, 15, 30, 40 をつないだ。 今回のモデルが以前のモデルより観測に良く合っていることが判る。

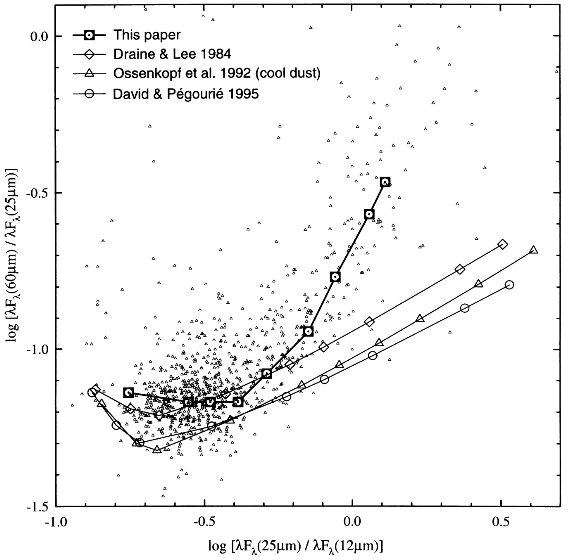図１２．ＩＲＡＳ二色図上の OH/IR 星

　６．結論