|
我々は天の川分子雲カタログをベル研 13CO サーベイの結果に温度
閾値を設けて作成した。このカタログから、二つのグループを作った。 (1) 近運動距離にあったとしても M > 105 Mo の雲。 (2) 遠運動距離にあったとしても M < 105 Mo の雲。 (l, v) 面上でのそれぞれの位置と速度を渦状雲の軌跡と較べた。各雲から 最短位置にある腕までの速度差を集中統計量として導入する。ほぼ全ても GMC は腕の近くにある。 | 小さい雲の密度は腕の近くで増大する。しかし 10 % くらいの雲はどの腕にも 付随していない。GMC と最近接腕との速度差中間値は 3.4±0.6 km/s で ある。一方小さい雲では 5.5±0.2 km/s であった。この差の一部は 雲集団の速度分散により、一部は銀河系回転速度場における雲と腕の位置の差 によるのであろう。簡単な評価によると、位置の違いによる速度差は重要でない。 つまり、データは GMC が渦状腕の中に封じられており、腕内での GMC の速度 分散は小さな雲より小さいという考えに整合する。 |
|
雲カタログ Lee et al. (2001) はベル研 13CO サーベイの結果に温度閾値を設けて天の川分子雲 カタログを作成した。このサーベイは 0.05° x 0.05° x 0.68 km/s のピクセル 2.3 107 個の 13CO データからなっている。 TR > Tth のピクセルを互いに繋がっているもの同士 でまとめて、(l, b, v) 空間内に"雲"を作った。Tth = 1 K と設定 して 1400 個の雲を検出した。 Stark, Lee (2005) に述べたように近運動距離と遠運動距離の問題がある。 |
巨大分子雲 GMC と小分子雲の選別 カタログには距離の範囲も載っている。距離に応じて雲の L(CO) そして 可能な雲質量 MC は変化する。巨大分子雲 GMC は次のように定義 する。 L(13CO) > 5 103 K km/s pc2 MC = 20 [L(13CO)/(K km/s pc2)] Mo の変換を 使うと、この基準は MC > 105 Mo に相当する。 雲質量の最小値、つまり近運動距離を採用した場合の質量、が巨大分子雲の基準を 満たした雲は 56 個であった。 一方、雲質量の最大値、つまり遠運動距離を採用した場合の質量、が巨大分子雲 の基準を満たさない雲は 1257 個であった。 どちらにも属さない、つまり距離の取り方によって巨大分子雲とも小分子雲とも 考える雲は 87 個であった。 |

|
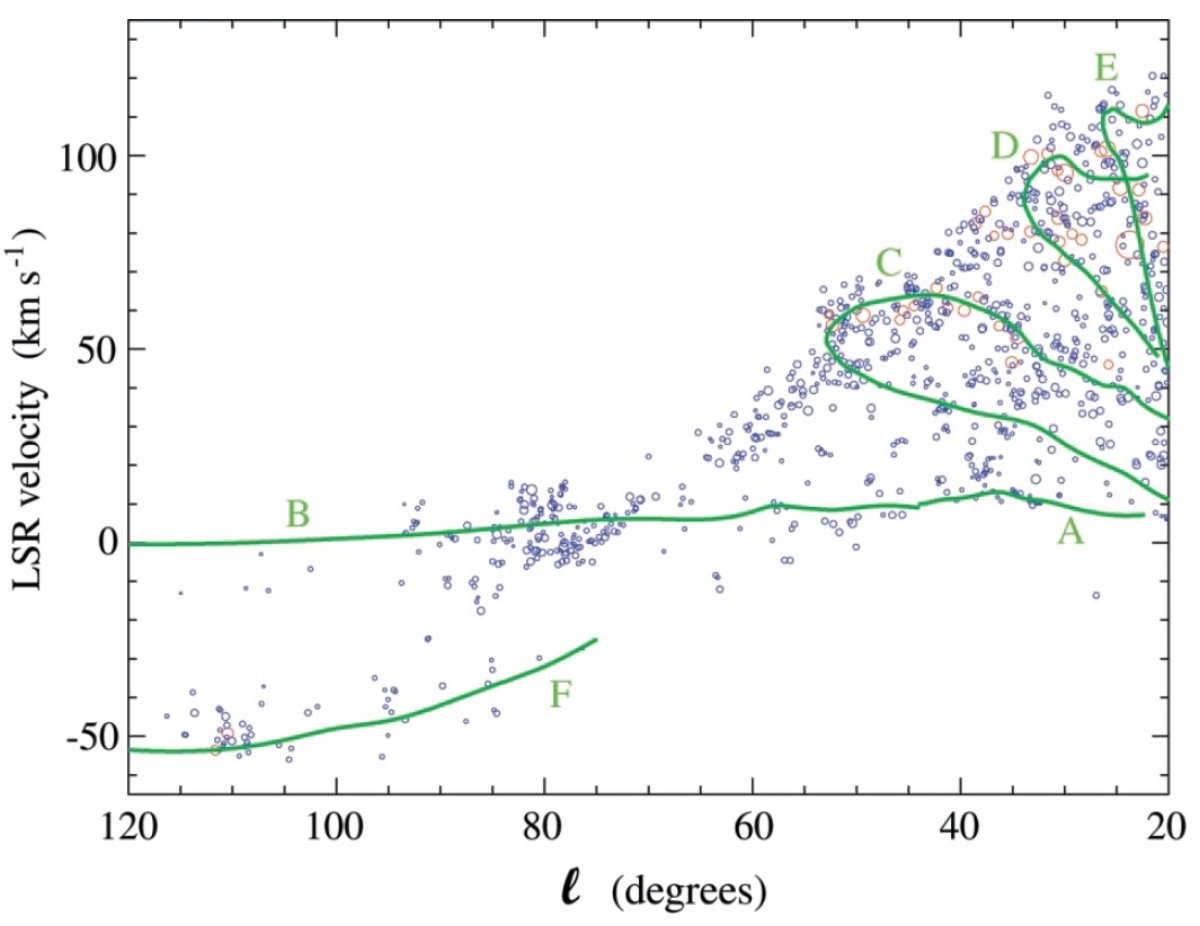
(l, v) 面上の渦状腕の筋と分子雲 図1には (l, v) 面上に渦状腕の筋と分子雲を描いた。渦状腕は、reifenstein et al 1970, Burton, Shane 1970, Shane 1972, Lindblad et al 1973, Simonson 1976 をまとめた。腕の名前は Cohen et al 1980 に従った。l = [20, 140] では研究間の同定は一致している。l < 20 ではそうではない。 それで、この論文では区間を l = [20, 140] に限った。この区間には確実巨大 分子雲 39 個、確実小分子雲 932 個が含まれる。 腕 A と B 腕 A と B は局所腕とリンドブラッドリングである。注意するが、この二つ は大きな構造ではなく、単に太陽に近いため大きく見えるに過ぎない。これら、 A−Fに関しては文献の結論は一致しているのでここに載せた。 |
巨大分子雲 Dame et al. (1986) が述べているように、巨大分子雲は「糸に通したビーズ玉」のように渦状腕に 乗っている。その例外はサジタリウス(C)と盾座(D)腕間の橋、(l, v) = (38, 90), の巨大分子雲である。腕 A と B には巨大分子雲はない。 |
|
集中統計量 |Δv| (l, v) 面上で分子雲と最近接の腕との間の v の差、|Δv| を集中 統計量と定義する。図2にはその分布を示す。 小さい雲の |Δv| 小さい雲の分布は全体の約 10 % を占める長い尾を持つ。その大部分は (l, v) = (55, 30) 付近に集中している。そのあたりでは視線が腕間空間を 通過し、接点も含む。接点付近では同じ速度に広い範囲の距離が対応する。これらの 雲は腕間星間雲のよい例である。 巨大分子雲の |Δv| 巨大分子雲のうち |Δv| > 14 km/s は5個しかない。内4個は先に 述べたサジタリウス - 盾座間の橋にある。 |
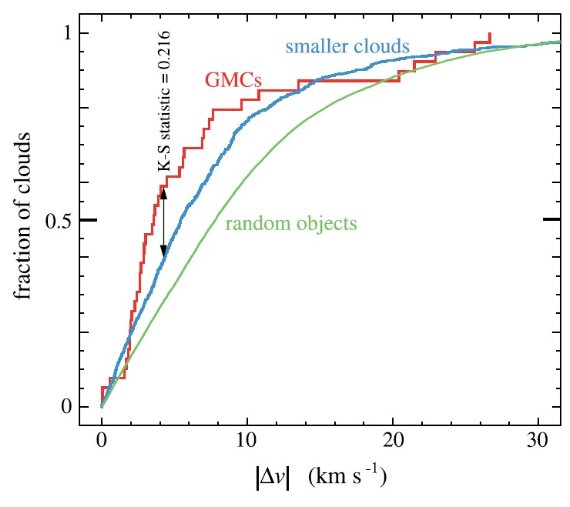 図2.|Δv| の累積分布。縦軸は総数で規格化。 赤=確実巨大分子雲 39 個。青=確実小分子雲 932 個。 その差=コロモゴロフ・スミルノフ統計量。 緑=銀河中心動径方向分布が分子雲と同じで、中心角方向には均等な分布の場合 のモデル速度差分布。 |
|
ビリアル質量の分布 図3には、Stark, Lee 2005 から選んだ距離の不定性の小さな雲に対して、 そのビリアル質量の分布を示す。 CO 質量の 85 % 以上が巨大分子雲に集中して いることが判る。 図2から、|Δv| 分布の中間値 m は巨大分子雲(GMC)で 3.4 km/s, 小さい雲(SMC)では 5.5 km/s である。Δv の分布をガウシアンと仮定する。 σa = Δv 分布の標準偏差 とすると、σa = 1.48 m なので、 σa(GMC) = 5.0 km/s, σa(SMC) = 8.2 km/s. σv = 雲の rms 速度分散 は、σv(GMC) = 4 km/s (Stark, Brand 1989), σv(SMC) = 7.8 km/s (Stark, Lee 2005 スケール高より)と 知られている。 σr = 銀河中心距離の差と回転曲線から生じる速度差。 とすると、 σa2 = σv2 + σr2 これから、典型的な銀河中心距離の差 Δr を求めると、 Δr = 220 pc となる。これは渦状腕の巾程度の大きさである。大きな Δv を示す腕間雲 を除くと、小さい雲も含めて、分子雲の大部分は渦状腕に含まれていると言って よいだろう。(l, v) 図上腕から離れているように見える配置は速度分散の反映で 説明可能である。 |
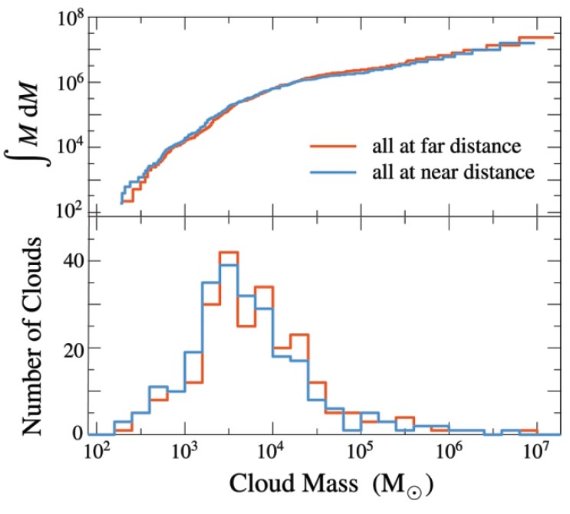 図3.ビリアル質量の分布。上:累積分布。下:微分分布。サンプルは Stark, Lee (2005) より距離不定性の小さい雲を選んだ。赤線=雲が全て遠運動距離にあると仮定 した場合。青線=雲が全て近運動距離にあると仮定した場合。 |