Kinematics of K Giants in the Outer Galactic Halo

　３．観測　

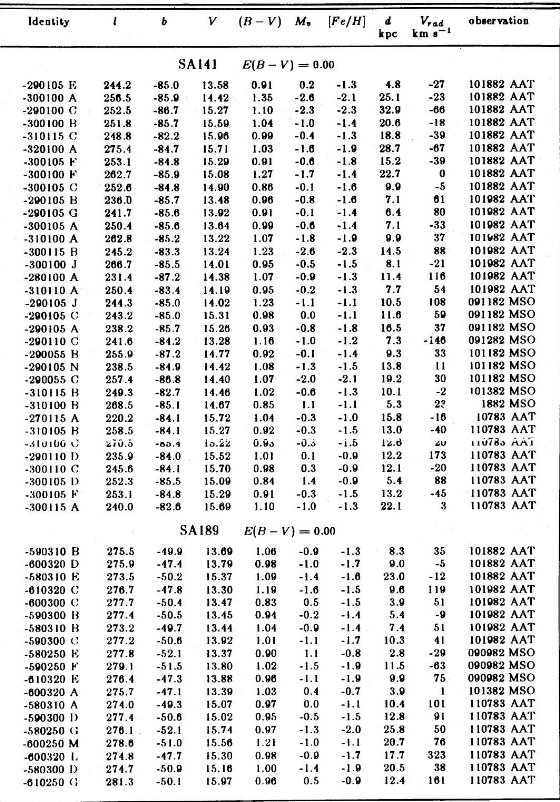
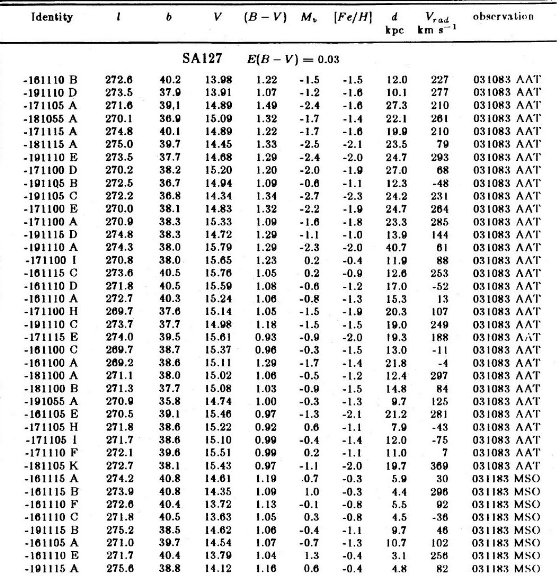
観測結果　 より高分解能スペクトルによる分類　 　ＡＡＴとＭＳＯ1.9m で巨星の分光観測を行った。分解能＝２Ａである。対象は 低メタル巨星である。SA 141, SA 127 の低メタル巨星はほぼ完全に観測が終わった。 メタルがより多い巨星の観測はまだ完了していない。SrII λ4078 と FeI λ4064 を較べると、Ｋ型巨星では Sr II ラインが強く、同じ温度の矮星 では Fe I ラインがずっと強い。低メタル星でもこれらのラインは検出でき、殆どの 星が巨星であることが確認された。このように高分解スペクトルで、対物プリズム 分類での矮星の混入は完全に阻止された。混入率は５％で、主に B-V ≈ 0.9 の温かいＧ型星で見られた。これらの星では分類に用いた MgH 帯が弱い。 視線速度と赤化　 　これらの星の視線速度は通常のクロスコリレーション法で求めた。表１にその 結果を載せた。B, V 測光は Siding Spring 1m 望遠鏡で行った。高銀緯で赤化は 小さいと予想されるので、 Burstein, Heiles 1982 赤化データを用いた。 メタル量　 　サンプル星は低メタル量なので、CaII H, K 線の強度からメタル量を求めた。 よく調べられた球状星団、47 Tuc([Fe/H] =-0.7), NGC 6752([Fe/H]=-1.5), NGC 6397([Fe/H]=-2.2), 二つの低メタル星 HD 122563([Fe/H]=-2.7), CD -38°245([Fe/H]=-4.5), により較正を行い、 Ca 指数 A(Ca) Norris, Freeman 1983 がメタル量 と B-V の関数として決められた。 こうして決められたＫ型巨星のメタル量は球状星団の範囲と重なり、平均では [Fe/H] = -1.5 であった。 絶対等級 Mv　 　星の (B-V)o とメタル量から、 球状星団の メタル量内挿CMD 上で絶対等級 Mv を 決める。 他の効果に較べると年齢効果は小さい。ハロー巨星は球状星団とほぼ同 年齢と考えられる。太陽からの距離は適用する E(B-V), V, Mv から決まる。 　表１に以上の結果が載せてある。分光観測が終了していないので、このリストは 完全ではない。座標とファインディングチャートは他に発表する。 観測エラー　 　個々の星毎に [Fe/H], 距離 のエラーが決められた。それらは表には載せていない が図には表示している。平均エラーは、(B-V), ± 0.02; V, ± 0.03; E(B-V), ± 0.01; A(Ca), ± 0.02; [Fe/H] 較正の固有エラー, ± 0.15; Mv 較正の固有エラー, ± 0.20 である。積算されたエラー は、[Fe/H] で ± 0.3, Mv で ± 0.5, 距離 d で ± 20 % である。視線速度では AAT 観測で ± 10 km/s, MSO 観測で ± 15 km/s である。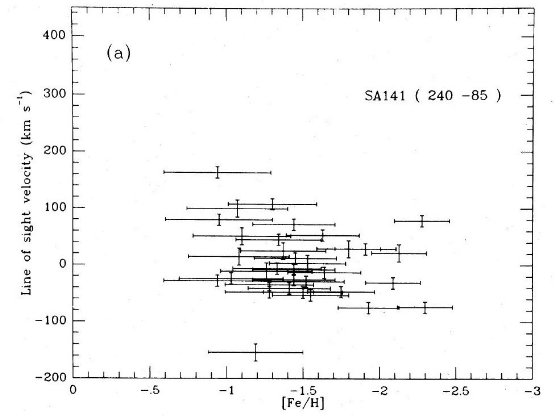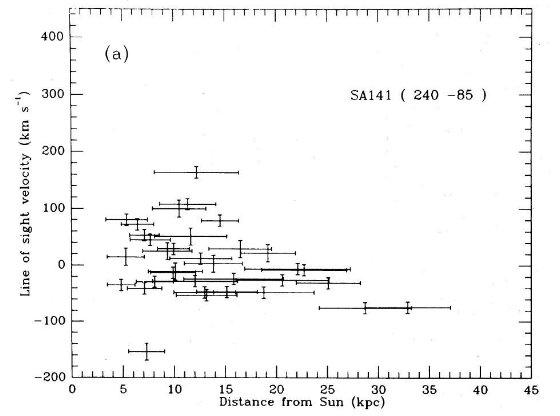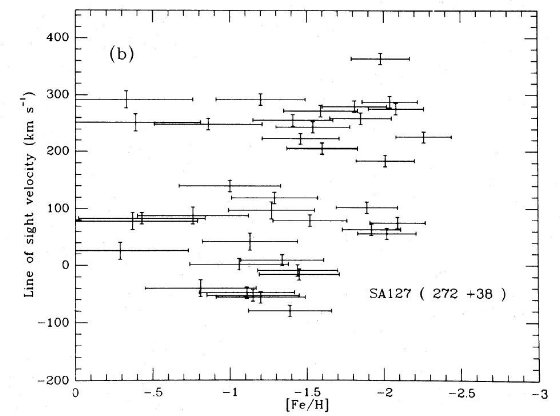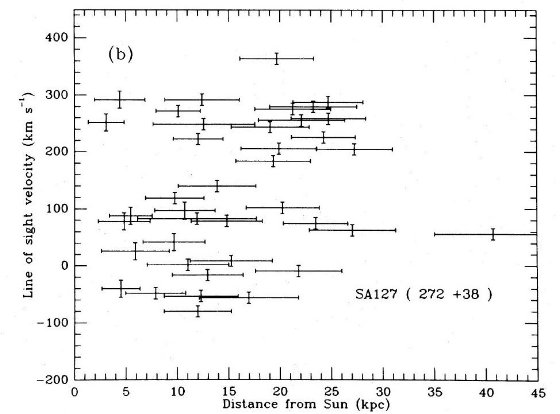 [Fe/H] > -1 の星　 　分光観測では対物プリズムデータから低メタルと判断された巨星を選んだが、 [Fe/H] > -1 の星もいくつか混ざりこんできた。ところがそれらの星の運動学 特性はより低メタルのグループと共通であった。そこでそれらの星も後の運動特性 の議論には混ぜた。図１にその例がある。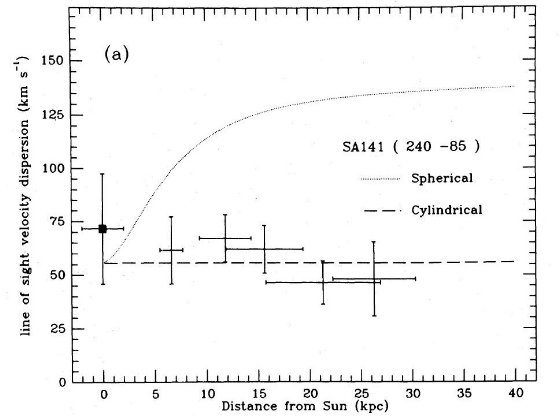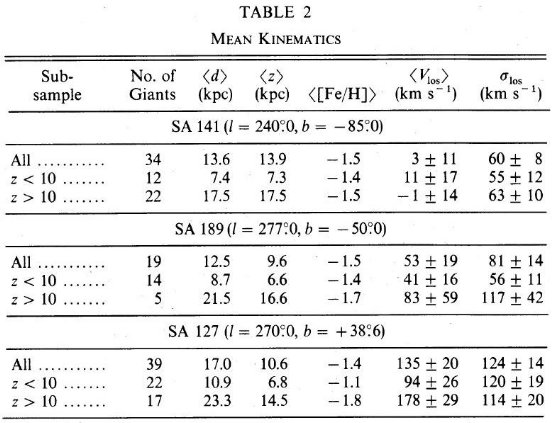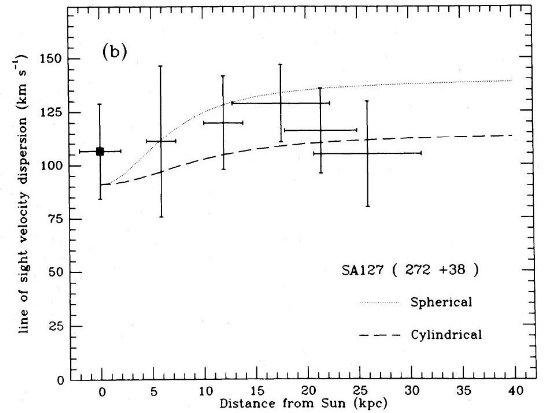 領域毎の平均値　 　表２には各領域毎の平均距離、光度、視線速度などを載せた。図２には太陽の 固有運動を補正した視線速度をプロットした。

図１(a)　SA 141 (SGP) での補正視線速度と[Fe/H]関係　 図２(a)　SA 141 (SGP) での補正視線速度と距離

図１(b)　SA 127(l=272°,b=+38°) での補正視線速度と[Fe/H] 図２(b)　SA 127(l=272°,b=+38°) での補正視線速度と距離

　４．解析　

４．１．SA 141 と SA 127　 メタル量と運動特性に相関が無い　 　ハローのメタル分布は我々の完全サンプルの分光観測が終わるまでは分からない。 今までのところは低メタル星の観測に重点が置かれている。得られたデータの範囲 では運動学特性とメタル量の間に相関はない。 平均視線速度　 　表２では SGP (SA 141) 方向の星の平均速度は予想されるようにゼロである。SA 127 方向 b = +38° l = 270°　では、より遠方の星の視線速度は 178 ± 29 km/s で、これは低い回転速度を持つ星に対して期待される値である。 SA 189 b = -50° l = 277° 方向の平均視線速度は表２では 83 ± 59 km/s で、ゼロ回転速度に対して期待される 140 km/s と有意な 差があるかどうかサンプル数が少ないので断言できない。 視線速度の分散　 　SGP と SA 127 との大きな差は速度分散である。SA 127 では速度分散が距離 によらずほぼ一定で、平均距離 23 kpc の 17 星に対し、速度分散は 114± 20 km/s である。SGP 低メタル星の速度分散も距離に依らないが その値は、平均距離 18 kpc の 22 星に対し、速度分散は 63± 10 km/s である。 分散の差は非球対称ハローを意味する。　 　これは驚くべき結果である。銀河中心ー太陽距離 R๏ ＝ 8.5 kpc とする。サーベイ領域は銀河中心方向に垂直な面内にある。星までの 距離 d &8811; R๏ では、視線速度は主に銀河中心から動径 方向成分を測ることになる。したがって、遠方ではどちらの領域でも視線速度 分散 σlos は速度楕円体の動径成分 σr に等しいと考えられる。ここで、速度楕円体が空間的には球対称であると仮定 する。つまり、楕円体の成分が中心からの距離 r のみの関数であるとする。 すると、 σlos はどちらの領域でも等しい値となるであろう。 ところが、観測はそれに反して大きな差を示し、これはハローが少なくとも 中心 25 kpc 以内で、運動学的に球対称から離れていることを意味する。 これはまた遠方ハロー星の速度分布が太陽近傍と同様に非等方であることを示唆 する。今や、外部銀河系の運動は空間的に球対称な銀河モデルでは記述できない のである。 第３積分？　 　軸対称な系で位相空間密度が二つの「古典的な」運動積分、エネルギーと 角運動量の軸成分、にのみよる時は速度分散の軸方向と動径方向成分の大きさは 等しい。(Jeans, 1916) 太陽近傍、外部ハローで見出された非等方性は第３積分 を持つ銀河モデルを要請する。 　この点で、Richstone 1980 のスケールフリーモデルは軸方向に伸びた速度 楕円を持っているのが我々の観測と一致していて興味深い。 図３(a)　SA 141(SGP)での補正視線速度分散

４．２．簡単な作業仮説　：　球モデル対筒モデル　 　簡単な仮説ーー速度分散成分がどこでも同じ、しかし等しくは無いーーを球座標 と軸極座標の二つで試してみよう。以下単に球仮説、筒仮説と呼ぶ。 　通常の球座標 (r, φ, θ) と 円筒座標(R, φ, z) を考えよう。 座標中心は銀河中心に置く。余緯度(colatitude) θ は北銀極から測り、 高度 z は北側が正とする。 　球仮説では、どこでも(σr,σφ,σ θ) = (140, 108, 55) km/s であるとする。この値は Hartwick 1983 による太陽近傍での低メタル巨星からの結果である。同様に、筒仮説では (σR,σφ,σz) = (140, 108, 55) km/s とする。 両モデルの視線速度分散　 　二つの仮説の下に σlos が距離によりどう変化するかを図３ に示した。 SGP 方向では二つの仮説が著しい差を生んでいることが分かる。 　次に観測の σlos はどうなるだろう？このため、5 kpc ずつ 離した指標距離をまず作り、その各距離ごとに ± 40 % の距離範囲にある星を 選び、それらの平均距離と速度分散を計算してその距離での分散とした。SA 141 に 関しては各副サンプルの平均速度をゼロと仮定した。したがって、図３a の分散はゼロ の周りの分散である。一方、図３b SA 127 は平均値の周りの分散である。副サン プルには同一星が複数回含まれる場合があるので注意。 　図３には、距離ゼロの所に太陽近傍の低メタル RR Lyr 星の速度分散(Woolley 1978) を置いた。Woolley の値は Hartwick の近傍巨星の値とも一致する。 　図３b からは SA 127 ではどちらの仮説も観測と合致することになる。しかし、図３a を見ると、 SGP SA 141 方向では、速度楕円の長軸がどこでも銀河中心方向を向いている という球モデルは明らかに観測と不一致であることが分かる。それに対し、筒モデルは よい一致が得られている。 図３(b)　SA 127(l=272°,b=+38°)での補正視線速度分散

４．３．他のハローサンプル　 Pier サンプルーのグループ化　 　Pier 1982, 1983 はハロー BHB 星のデータを数領域で得た。それらを幾つかの グループに分けた。 (1)　M3 HB のカラー・光度関係を使って、星のカラーから分光視差を決める。 　　　Pier サンプルの大部分は太陽距離 2 - 10 kpc だが、< 4 kpc は捨てる。 (2)　第１領域の SGP では |b| > 81°: はたった 23 BHB しかない。 (3)　反中心(l = 186°, b = -55°)方向に 1 領域、中心方向に 3 領域, b = -57°, -28°, -17°。 (4)　回転領域 b = -60°, で l = 90°, 270°, の領域がある。 (5)　我々の SA 189 サンプルも別のハローサンプルとなる。 球モデルと筒モデルの優劣　 　これらのグループに対し、平均距離、速度分散 σlos、 などを 表３にまとめた。球モデル、筒モデルのそれぞれで計算した分散値を図４で比較した。 明らかに筒モデルの方が優れている。球モデルが観測値と最も離れるのは SGP (領域a) と l = 0° 方向の領域 c, d である。 図４(a)　Pier フィールドでの視線速度分散の比較:球モデル

SGP 領域では視線方向が、筒モデルの場合は 速度楕円の短軸に沿う向きで、球モデルでは長軸に沿う向きになる。一方で、l = 0° で銀緯が中くらい、距離 6 kpc 付近だと球モデルでの短軸方向を見ることに なる。 ここで提出した筒モデルは太陽から　3 - 25 kpc の距離で観測と合う最も簡単な モデルである。勿論、球モデルでも速度楕円の形を距離により変えるなどの複雑化 で l = 0° 方向のデータと合わせることは可能である。しかし、それでも SGP 方向で分散が小さくなることは説明できないだろう。 ４．４．回転速度　 ハロー回転速度と太陽回転速度　 　中銀緯の視線速度サンプルは銀河系の回転を調べるのに使える。太陽の回転速度 Vo とハロー回転速度は片方を決めるともう片方が決まるという関係である。 SA 127 と SA 189 にある z > 10 kpc の遠方巨星 22 個を考えよう。これらが 平均して回転ゼロとすると、 Vo = 212 km/s が得られる。球状星団と類似の回転 速度 +60 km/s を採用すると、Vo = 241 ±: 34 km/s が得られる。これら の値は現在受け入れられている Vo = 220 km/s に近い。したがって、遠方ハロー 巨星はゆっくりとした回転種族に属する。 　興味深いのは、これらの回転速度を太陽近傍の特別なグループの星の運動と較べる ことである。それらは Sandage 1969 によると、⟨V⟩ = 192 ± 13 km/s を与える。何の話だ？ 逆回転星流？　 　SA 127 の回転速度を評価する際、遠方星は単一種族であると考えてきた。しかし、 図１(b), 図２(b) を見ると、大体 50 km/s と 250 km/s の２種族があると考える のがよさそうである。SA 127 の 39 星に対する統計テストの結果はこれらの分布は 単一ガウシャンから有意に外れてはいない。しかし、図に現れた双耳峰性を信じると 低速度成分はハローの高速回転成分で、高速成分は逆回転星流を表わす。どちら の成分も比較的冷たく、 σlos ≈ 50 km/s である。 逆回転星流の可能性は Rodgers, Paltoglou 1984 の逆回転球状星団の起源に関する 議論を思い起こさせる。しかし、現段階ではこの星流の証拠は弱いのでここでは 止めておく。 図４(b)　Pier フィールドでの視線速度分散の比較:筒モデル

　５．議論