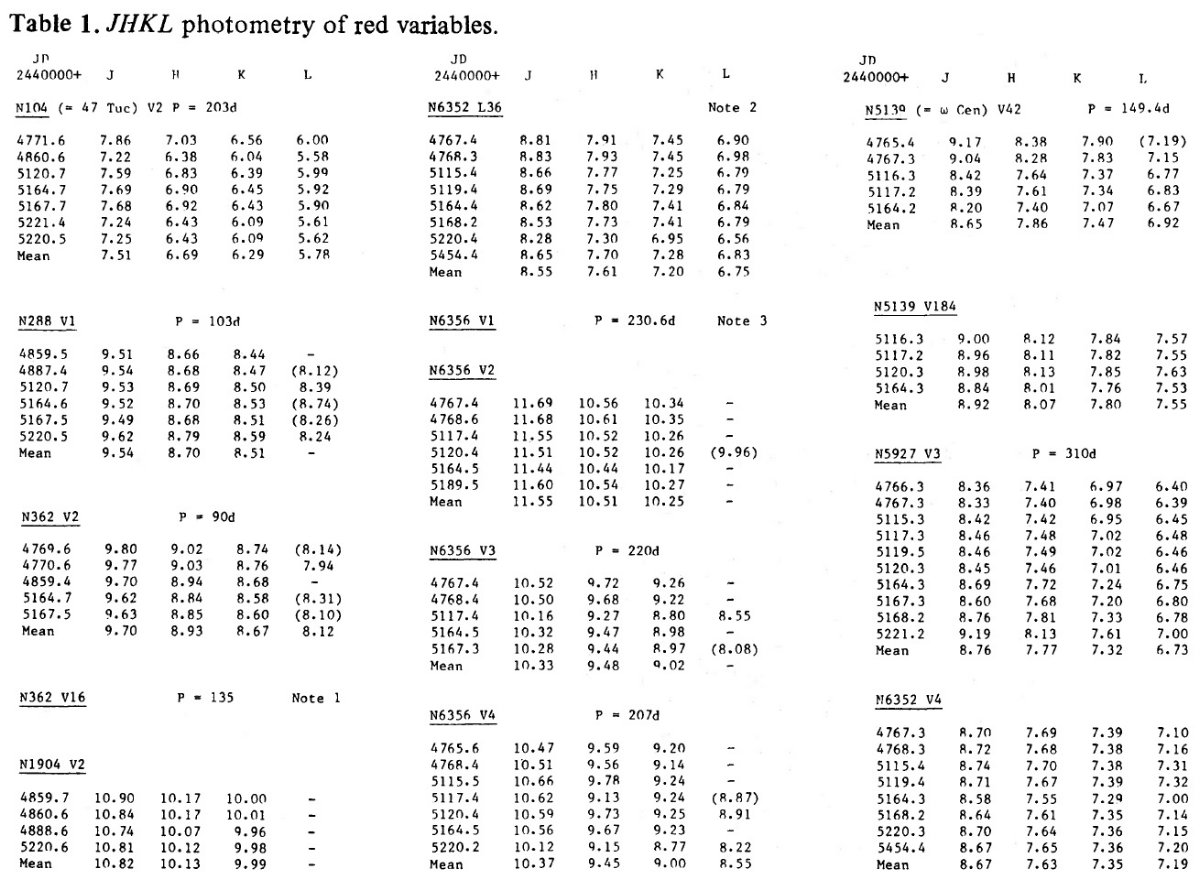
| 15 球状星団中の 31 赤色変光星の JHKL 測光を行った。ミラ型星の測光から 絶対輻射等級を導き、さらに Mbol - log P 関係を導いた。 | 球状星団の周期光度関係は LMC ミラの場合と違っていた。その原因としては、 球状星団および、または、LMC の距離指数に系統誤差が含まれているか、または 球状星団ミラと LMC ミラの間に何か基本的な違いがあるか、のどちらかである。 |
|
ミラの周期光度関係 ミラの絶対等級は距離指標として有用である。 Robertson, Feast (1981) は銀河系ミラの統計視差と距離が既知のミラ型星から絶対輻射等級を求めた。 それに続いて、 Glass, Lloyd Evans (1981) は LMC ミラ型星が散らばりの少ない周期光度関係に従うことを発見した。 星団ミラ 12 の高メタル球状星団にミラ型星が見つかっている。星団までの距離は RR Lyr 星の等級または、それが無い場合、水平枝の絶対等級と見かけ等級 との差から決める。いくつかの星団では主系列フィットから距離を決める。 |
星団距離 JHKL 測光とそれから決まる見かけ輻射等級に、赤化補正、 Glass, Lloyd Evans (1981) の周期光度関係を組み合わせれば、球状星団までの距離をより正確に決める ことが出来るだろう。ただし、それには LMC と球状星団が同じ周期・光度 関係を有することが前提である。 ミラから RR Kyr へ 我々は可視域で決まった星団距離を用いて、ミラの絶対等級を求め、 星団ミラの周期光度関係を LMC ミラのそれと比較する。星団ミラの観測から 距離が決まれば、 星団 RR Lyr 星の絶対光度を決めることが出来、さらに それらがメタル量にどう依存するかも調べられる。 (初めは RR Lyr から星団距離を言って たのに、最後は逆転してる。本当? ) |

|
輻射等級の決定 フラックスで平均した輻射等級はミラからの総輻射量を表す最適な表現である。 しかし、光度曲線を決めるにはデータ点の数が足りない。数値実験の結果、 極大等級と極小等級の平均がフラックス平均をかなり正確に与えることが判った。 本論文の輻射等級はそのようにして求められた。 水蒸気吸収の影響 Robertson, Feast (1981) は水蒸気吸収が輻射等級に影響することを指摘した。そのため、我々の求めた 輻射等級は 1/10 等か 2/10 等明るすぎるかも知れない。 |
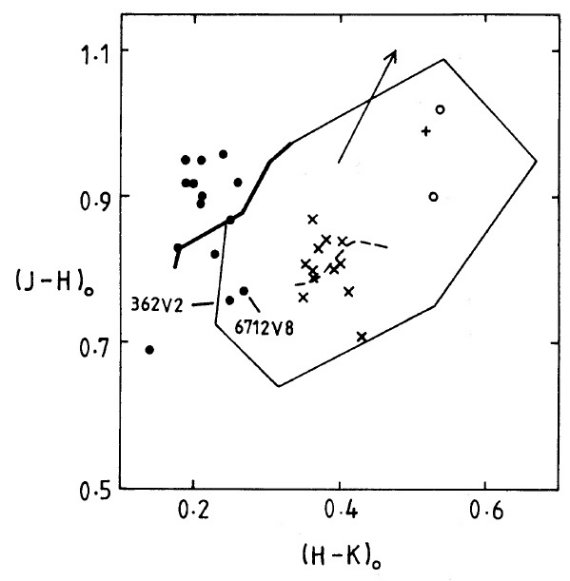 図1.星団赤色変光星の2色図。太い実線=フィールド巨星。実線枠=フィー ルドミラの領域。矢印=赤化。黒丸=非ミラ。バツ=ミラ。白丸= Terzan5 の 二つのミラ。プラス= V6 in NGC6356. 破線=球状星団ミラと同じ周期帯を持つ フィールドミラの平均経路。 |
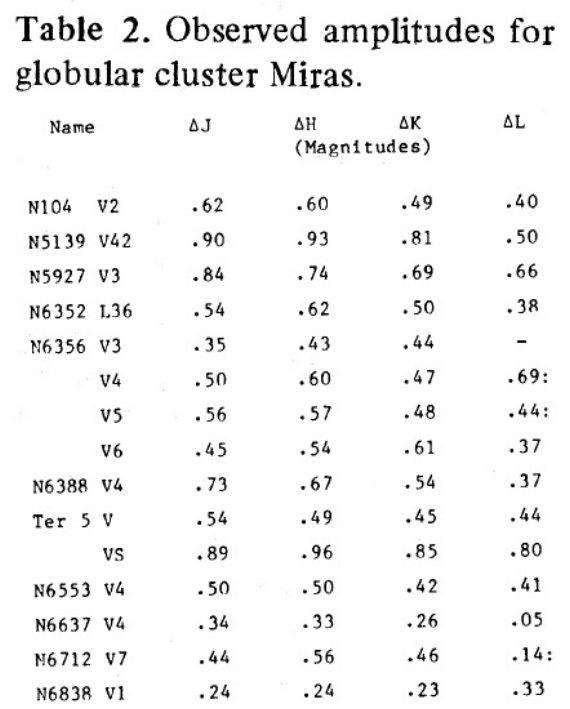 表2.球状星団ミラの振幅 |
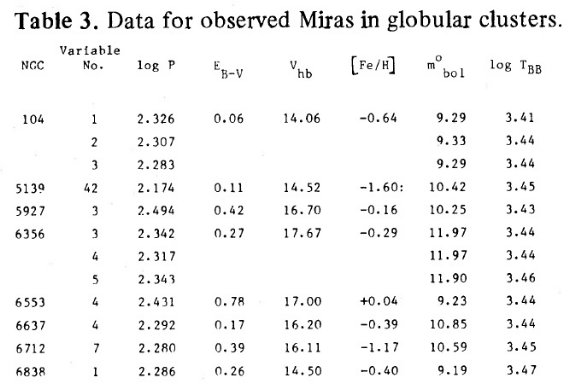 表3.球状星団ミラのデータ |
|
Mbol の修正 Glass, Lloyd Evans (1981) では平均 mbol を数回の測光の平均値として定義した。我々と同じ 方法で平均 mbol を決めるため、各回の測光値を使って、決め直し た。炭素星の C7 と C153 は外した。E(B-V) = 0.04 を採用した。 |
新しい周期光度関係 その結果、新しい周期光度関係として、 mbol0 = 19.99(±2.02) - 2.435(± 0.85) log P LMC の距離指数を (m-M) = 18.69 として、 Mbol0 = 1.30 - 2.435log P を得た。 |
|
メタル量 メタル量は Zinn 1980 から採用した。ω Cen のメタル量が一定でない ことは明らかである。我々は [Fe/H] = -1.6 のケースと -1.2 のケースを扱った。 |
水平枝等級 水平枝等級には Harris 1980 の表を用いた。表3には E(B-V), Vhb, [Fe/H] を載せた。 |
|
HB 絶対等級 RR Lyr または HB の等級に関して議論が収束していない。 Harris 1980 は Mv(HB) は高メタルほど暗くなるという立場である。最近よく使われるのは、 [Fe/H] ≤ -1.0 では Mv(HB) = +0.6, [Fe/H] > -1.0 では Mv(HB) = +0.9, というものである。ミラを持つ星団は高メタルなので、 Mv(HB) = +0.9 とする。 星団ミラの光度 星団ミラの輻射絶対等級は RR Lyr の絶対等級を基準に次の式で求める。 mbol0 - Mbol = Vhb0 - MV(HB) 図2にその結果を示す。実線は、LMC ミラに対して我々が新しく求めた 関係である。星団ミラの周期光度関係の相関は緊密に見える。しかしそれは LMC の関係と同じでない。 球状星団ミラの周期光度関係 球状星団ミラの周期・光度関係は、 Mbol = 4.84(±2.10) - 3.73(± 0.90) log P (V42 を抜いて) Mbol = 6.88 - 4.59(± 0.90) log P (V42 を含んで) となる。 |
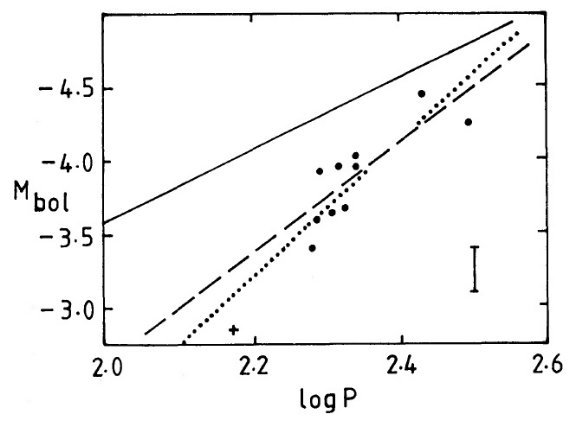 図2.球状星団ミラの Mbol - log P 関係。右下の縦棒は観測エラーの ± 0.15 mag を表す。実線= LMC の PLR. 点線= ω Cen の星を入れる。 破線= ω Cen の星を入れない。十字= ω Cen の星。 |
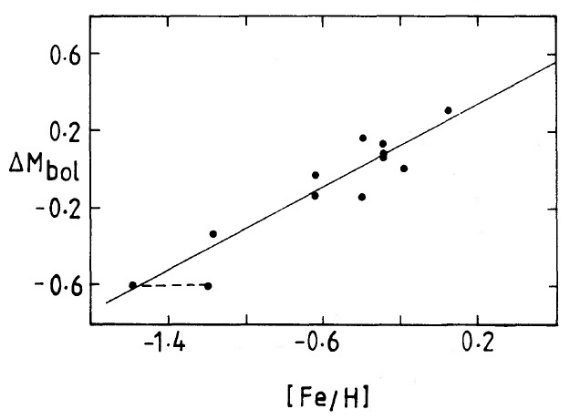 図3.Mbol = 1.85 - 2.435log P からの残差 ΔMbol と [Fe/H] との関係。ω Cen V42 の二つの仮定 [Fe/H] は点線でつないだ。 LMC ミラの勾配を星団ミラに適用すると LMC と球状星団とでの勾配の差は統計的には有意でない。そこで、 LMC ミラの勾配を星団ミラに適用してフィットすると、 Mbol = 1.85 - 2.435log P となる。ゼロ点の差は 0.55 mag である。 球状星団ミラの周期・光度関係は LMC と差あり こうして、イントロダクションで述べた疑問に対して肯定的な解答が得られた。 すなわち、球状星団ミラの周期・光度関係は LMC の場合と比較して、同じ勾配と するとゼロ点が異なり、おそらく勾配にも差がある。 観測 Mbol とフィット値 Mbol = 1.85 - 2.435log P との差 ΔMbol と [Fe/H] の関係を図3に示す。この関係を フィットすると、 ΔMbol = 0.24 + 0.54 [Fe/H] である。全体としては Mbol(球状星団) = 1.85 - 2.435log P - 0.24 - 0.54 [Fe/H] Mv(RR) にメタル効果がある? 上の式は Mbol がメタル量に強く依存する表現となっている。 しかし、この関係は全ての星団で Mv(RR) = 0.9 mag であることを仮定して導 いたものである。 Mv(RR) のメタル量効果を無視した結果が Mbol に反映しているのかも知れない。仮に Mv(HB) = 0.9 の代わりに Mv(HB) = 1.14 + 0.54[Fe/H] (2) というメタル効果を仮定したら、ミラの Mbol はメタル依存性が無いことになってしまう。 |
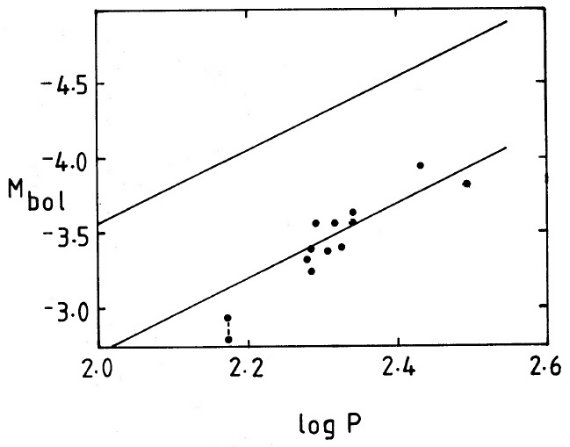 図4.Mbol - log P 関係。ここでは、Mbol を Sandage (1982a) の Mv(RR) 関係を用いて求めた。上の直線= LMC 関係。下の直線= 同じ勾配で星団ミラにフィット。繋がれた2点は Cen V42 RR Lyr 星の絶対等級のメタル量効果 Sandage (1982a), Sandage (1982b) は、球状星団の Oosterhoff 効果は、星団 RR Lyr 星の絶対等級がメタル量と 以下の関係にあるなら説明可能であることを示した。 Mv(RR) = 1.389 + 0.348[Fe/H] (3) ここに、[Fe/H] は Zinn 1980 から採った。[Fe/H] > -1.2 の球状星団 には RR Lyr 星が殆どない。しかし RR Lyr のない星団では、水平枝絶対等級 Mv(HB) を Mv(RR) に相当すると考えると、 球状星団 Mv(HB) にメタル依存を考慮 球状星団 Mv(HB) に Sandage 1982 のメタル依存、式 (3) があると仮定して、 球状星団距離を修正し、最終的な周期光度関係を導いた。 Mbol = 2.15 - 2.435log P (4) 球状星団と LMC の周期光度関係のゼロ点の差は LMC 側が 0.85 等明るく出る。 Mv(HB) にメタル依存を考慮した結果、rms = 0.11 等にまで下がった。 |
球状星団と LMC の差が本当かどうか、エラーの原因となり得る問題を以下で
議論する。
7.1.球状星団距離は正しいか?Sandage (1982a) は暗すぎ?もし、LMC 距離が正しいなら、 Sandage (1982a) が提案した Mv - [Fe/H] 関係は、実際より 0.9 mag 暗いことになる。つまり、 Mv(RR) = 0.489 + 0.348[Fe/H] ならば LMC と球状星団みらの周期光度関係は一致するのである。その場合、 [Fe/H] = 0 での RR Lyr は Mv = 0.5 mag で、低メタル RR Lyr 星はさらに 明るいということになる。 RR Lyr Mv のメタル依存性1 Frenk, White 1982 は球状星団の分布の中心として銀河中心距離 Ro = 7.0 kpc を求めた。彼らは Sandage 1982a の関係をゼロ点を 0.2 mag 明るくして採用した。 彼らのゼロ点を上に示唆したように、つまり更に 0.7 mag 明るくすると、 Ro = 9.7 kpc となる。これは、Glass, Feast 1982 が LMC ミラの周期光度関係を バーデの窓にあるミラ型星に適用して得た値 Ro = 9.2 kpc と一致する。しかし、 一方で、Glass, Feast 1982 は、彼らの結果が Oort, Plaut 1975 によるバーデ の窓の RR Lyr の ⟨Mv⟩ = 0.5 mag と良く合うとしている。前節で 示した式によると、それは [Fe/H] = 0 を意味する。この点に関して、 Butler, Carbon, Kraft 1976 はバーデの窓にある9個の RR Lyr の平均メタル 量を ⟨[Fe/H]⟩ = -0.65 とした。また、 Butler, demarque, Smith 1982 は LMC の NGC 1783 フィールドの RR Lyr に対し、 ⟨[Fe/H]⟩ = -1.4 を得た。 RR Lyr Mv のメタル依存性2 フィールド RR Lyr と星団 RR Lyr が同じかどうかに関しても議論がある。 Pel Lub 1978 は Sandage (1982b) と勾配は同じだが、ゼロ点は 0.5 mag 明るい関係を得ている。一方では、 Heck, Lakaya 1978 は低メタルほど RR Lyr 光度が暗くなるという、 Sandage と 逆の結果を得た。更に 0.9 mag 明るいゼロ点に関しては、星団年齢が 3 Gyr 明るくなるという問題もある。 |
7.2.LMC 距離がおかしい?(m-M)o = 17.8 ?LMC 距離指数が (m-M)o = 17.8 ならば、不一致は解消する。その時には、 Glass, Feast 1982 が求めた銀河中心距離は 6.3 kpc となり、Frenk, White 1982 の結果と一致する。この場合、Graham のフィールドの RR Lyr は Mv = 1.28 となる。これは、 Butler et al 1982 の得た [Fe/H] = -1.4 とは ぎりぎり合う。 セファイドと矛盾 しかし、この短距離 LMC はセファイドの結果と合わないという問題がある。 セファイドが強い赤化を受けているという逃げ道が考えられるが、 Martin et al 1979 の結果はそれがあり得ないことを示す。 |
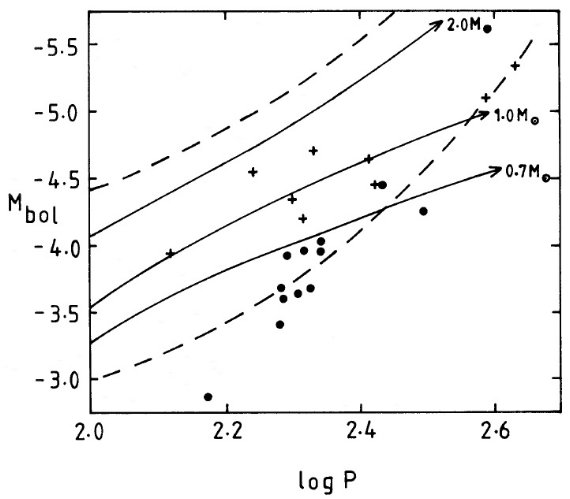 図5. Wood, Bessell, Fox (1983) の Mbol - log P 図。バツ= LMC ミラ。黒丸=球状星団ミラ。 Wood, Bessell, Fox (1983) の図6で、彼らは LMC AGB 変光星が Mbol-logP 面上の限られた領域に存在 することを示した。それによると、与えられた光度に対しては周期のはっきり した上限が付く。図5には彼らの結果から、 M = 0.7, 1.0, 2.0 Mo の星の進 化経路を、第一倍音とやや低メタルの仮定で、示した。バツ印は Glass, Feast 1982a による LMC ミラ、黒丸は球状星団ミラである。 進化経路 図5上で、LMC 長周期変光星は破線の間に一面に散らばっているが、それでも M = 1 Mo 経路に沿って密集している事は明らかである。一方、球状星団ミラ もやはり集まっているがその場所は、0.7 Mo 経路である。これは球状星団 AGB 星に期待される質量である。 脈動定数 Q Glass, Feast 1982b は脈動定数 Q に対し次の式を与えた。 log(QM-1/2) = logP + 0.3Mbol 3 logTeff - 12.71 Robertson, Feast (1981) は Teff = TBB として良いことを示した。表3の第8列では TBB を示した。それを見ると殆ど同じ値なので logTBB = 3.45 と固定値を入れる。式 (4) の周期光度関係を上の式に入れると、最終的に log(QM-1/2) = -1.72 + 0.27 logP |
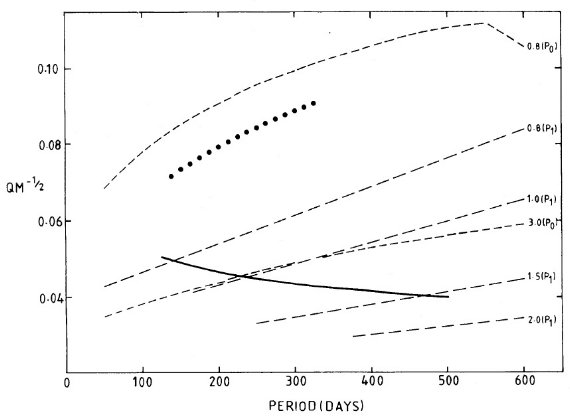 図6.Glass, Feast 1982b による QM-1/2 と P の関係。点線= 球状星団ミラ。実線= LMC ミラ。 図6=周期と QM-1/2 の関係 図6にその関係をプロットした。これは基本的には Glass, Feast 1982a の図3 と同じである。破線= Wood 1981 の質量、脈動モード毎の理論曲線。点線= 球状星団ミラ。実線= LMC ミラ。点線の位置からは、星団ミラが基本振動なのか、 第1倍音なのか決められない。しかし、星団ミラの質量が LMC より小さいことは確かな ようである。 ミラの光度 P ≥ 100 d の球状星団では、一つの球団のミラの平均周期は測光で決めた メタル量 [Fe/H] と強い相関があることが、 Feast 1981, Lloyd Evans 1983b により指摘されている。この周期・メタル量相関に、周期光度関係、とミラが AGB先端にあることを結合すると、あるメタル量の星団では星がミラになる のは臨界光度に達した時であることが判る。また、球状星団質量では、 [Fe/H] ≥ -1.2 がミラになるのに必要であることも分かる。 LMCの古い種族はミラにならない LMC のメタル増加史は MW と異なる。LMC で最も古い低質量星のメタル量は 低すぎて、ミラを形成するには不足だったらしい。比較的最近になってメタル量と 質量の組み合わせがミラの出現を許すようになったのであろう。 |
| LMC ミラは球状星団ミラと異なる。この二つの種族を見分ける方法が分かるまで、 ミラを距離決定に使うのは無理である。 | 一方、 RR Lyr の Mv に基づく球状星団距離と、セファイド Mv に基づく LMC 距離には誤りがあるかも知れない。エラーの修正が二つの周期光度関係 を近づける可能性がある。 |